Квадратичная функция, её свойства и график

1.

2.

Определение
Квадратичная
функция
Построение
графика
Свойства

3.

Определение:
Квадратичной функцией
называется функция, которую
можно задать формулой вида
y = ax2 + bx + c,
где x – независимая переменная, a,
b и c – некоторые числа, причем
a≠0.

4. Из предложенных функций выберите квадратичную функцию

4
1) у
х
2
2) у 6 х
х
3) у 2
х 8
4) у 5 6 х
5) у ( х 7) 1
2
6) у 6 х

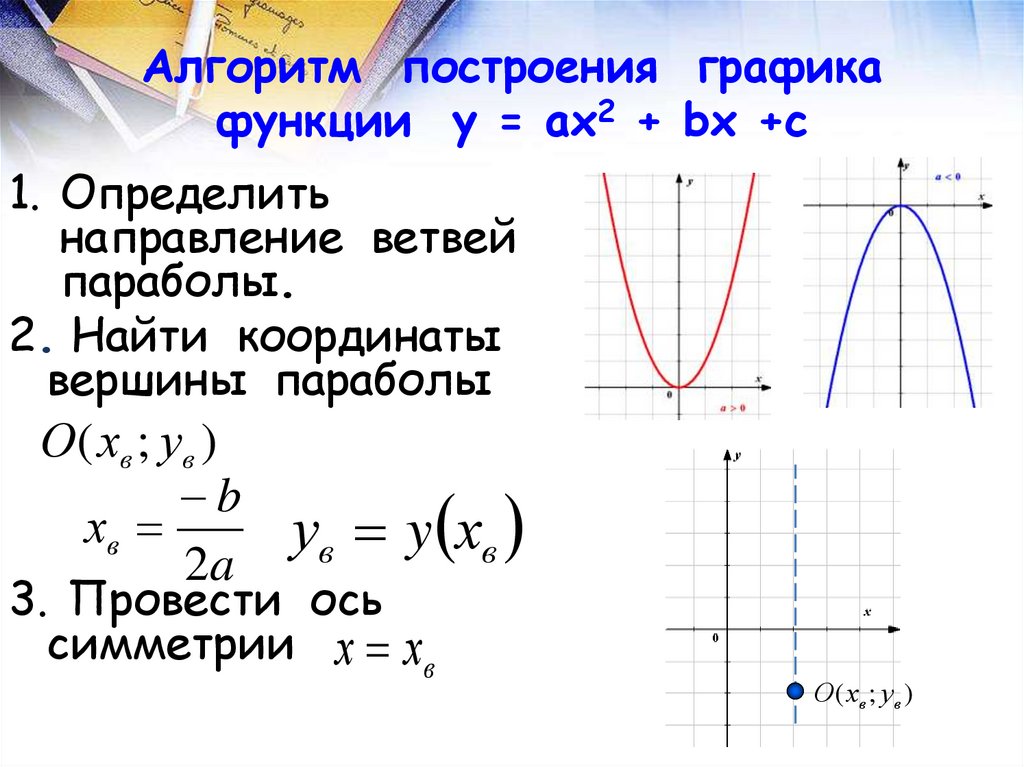
5. Алгоритм построения графика функции у = ах2 + bх +с

1. Определить
направление ветвей
параболы.
2. Найти координаты
вершины параболы
О ( хв ; ув )
b
хв
2a
ув y хв
3. Провести ось
симметрии х хв
О ( хв ; ув )

6.

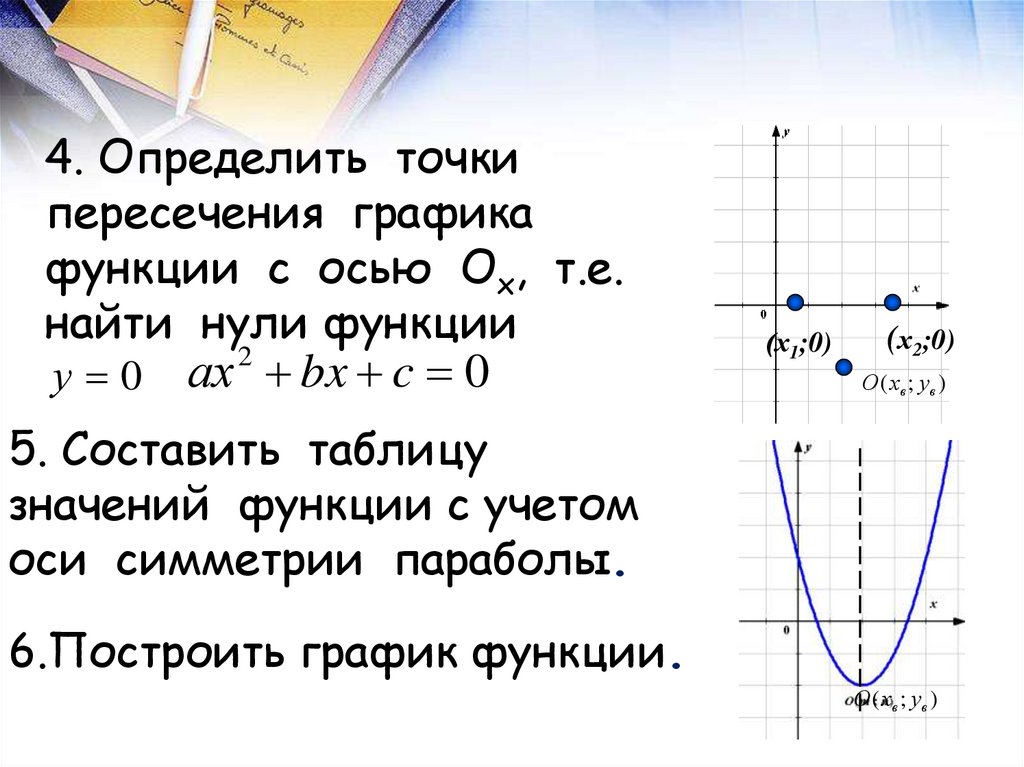
4. Определить точки
пересечения графика
функции с осью Ох, т.е.
найти нули функции
2
у 0 ах bx c 0
(х1;0)
(х2;0)
О ( хв ; ув )
5. Составить таблицу
значений функции с учетом
оси симметрии параболы.
6.Построить график функции.
О ( хв ; ув )

7.

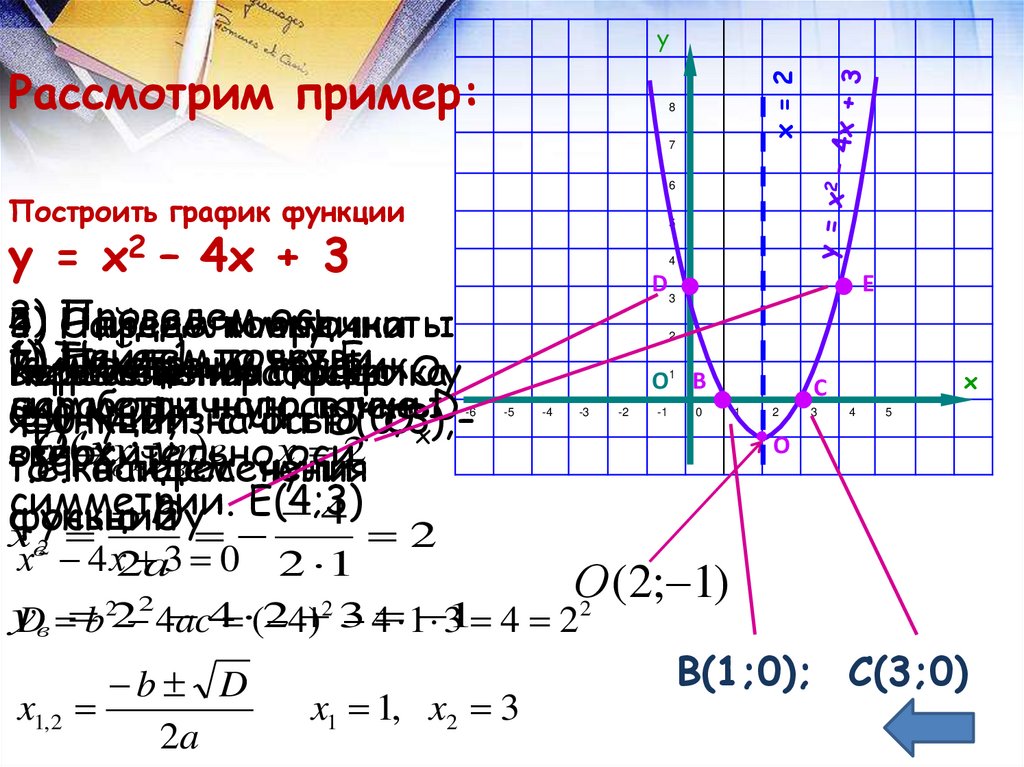
Рассмотрим пример:
х = 2
у
8
7
6
Построить график функции
5
у = х2 – 4х + 3
4
3)
Проведем
ось
2) Найдем
4)
5)
Определим
координаты
точку
точки
1)
6)
Т.к.
Найдем
а=1,параболы
то
точку
Е Оу
симметрии
7)
Построим
график
вершины
пересечения
пересечения
светви
графика
осью
параболы
симметричную
направлены
точке
функции
х=0,
функции
у=3, значит
с осью
D(0;3)
ОхD, –
х;в ,ут
.е. хоси
2
Ох ( хнайдем
вверх.
относительно
впересечения
в)
т.е.
точка
нули
симметрии.
Е(4;3)
b
4
функции
с
осью
Оу
х
2
-6
D3
Е
2
О1 В
-5
-4
-3
-2
-1
0
х
С
1
2
О
3
4
5
хв2 4 х2 a3 0 2 1
О
(
2
;
1
)
2
у
Dв b22 4
ac4 (2
4
)2 3
4 1 31 4 22
b D
x1, 2
2a
x1 1, x2 3
В(1;0); С(3;0)

8. Свойства квадратичной функции у = ах2 + bх +с, при а>0

Свойства квадратичной функции
у = ах2 + bх +с, при а>0
D>0
1. Область
определения
2. Область
значений
3. Нули функции
4.Возрастание
убывание
функции
D=0
D( у ) R
Е ( у ) ув ;
b
b D
нулей нет
x1, 2
x1, 2
2a
2a
; xв функция убывает
xв ; функция возрастает
5.Положительны ; х х ; , у 0
1
2
; х1 х1; , у 0
е отрицательные
х ; х , y 0
значения функции 1 2
6.Наибольшее
или наименьшее
значение функции
D<0
; , y 0
унаим ув
Для у=ах2+bх+с, при а<0, заполните таблицу самостоятельно

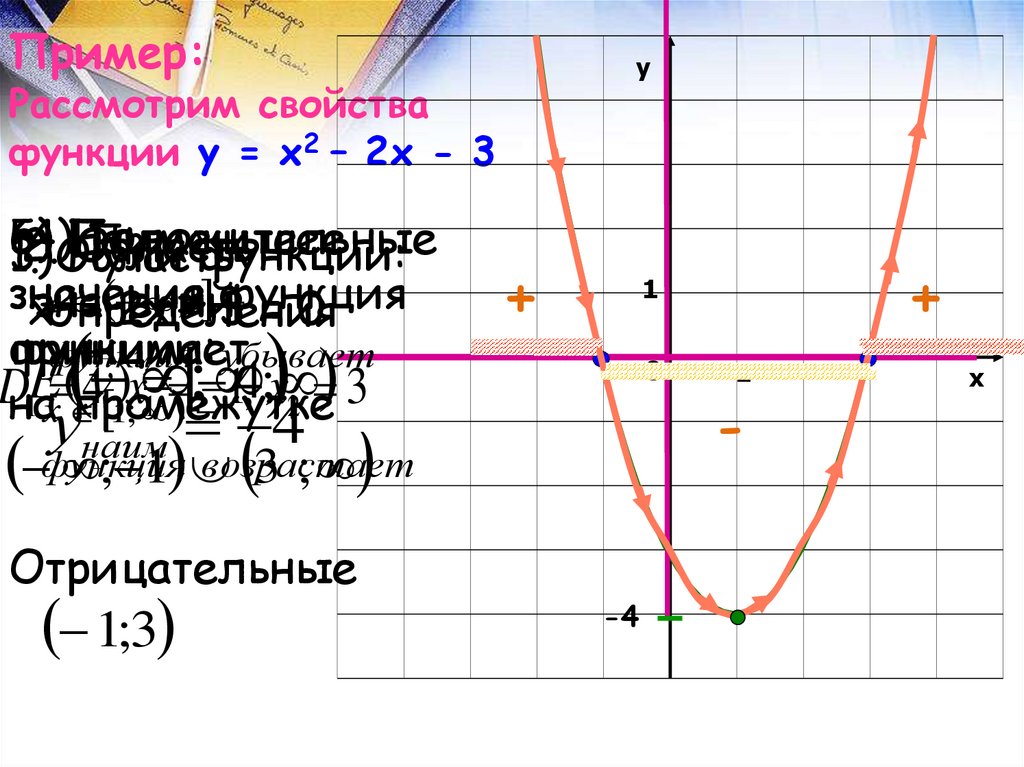
9. Пример: Рассмотрим свойства функции у = х2 – 2х - 3

Пример:
у
Рассмотрим свойства
функции у = х2 – 2х - 3
6)
5)
4)Область
Положительные
Наименьшее
При функции:
Область
3)
Нули
1.2.
значения
значение
функция
2 –
хопределения
;1- 3
=0
хзначений
2х
принимает
функции:
функция убывает
Е
(
у
)
4
;
;
Dна
4
x
1
,
x
3
1х
1
2
промежутке
у 1; 4
+
0
возрастает
функция
3 ;
; 1
наим
Отрицательные
1;3
+
1
-4
1
-
х

10.

Ответьте на
вопросы:
1. Назовите координаты
вершины параболы;
2. Назовите ось
симметрии параболы;
3. Назовите нули
функции;
4. Назовите промежутки
возрастания и убывания
функции;
5. При каких значениях х,
значения функции
положительны, а при
каких отрицательны;
6. Назовите наибольшее
или наименьшее
значение функции.
у
4
3
2
1
-4
-3
-2
1
-1 0
-2
-3
-4
-5
2
3
4 х

11.

12.

13.

14.

15.

16.

17.

18.

Спасибо за урок.