Похожие презентации:
Объединение множеств
1.
2.
№ 1124 Верно ли, что:а) 0,75 N верно
б) 68 N
неверно
в) 3,7 Z верно
г) 54 Z неверно
6
д)
Q неверно
11
12
Q неверно
е)
17
ж) 0 Q
неверно
з) 19 Q неверно
3.
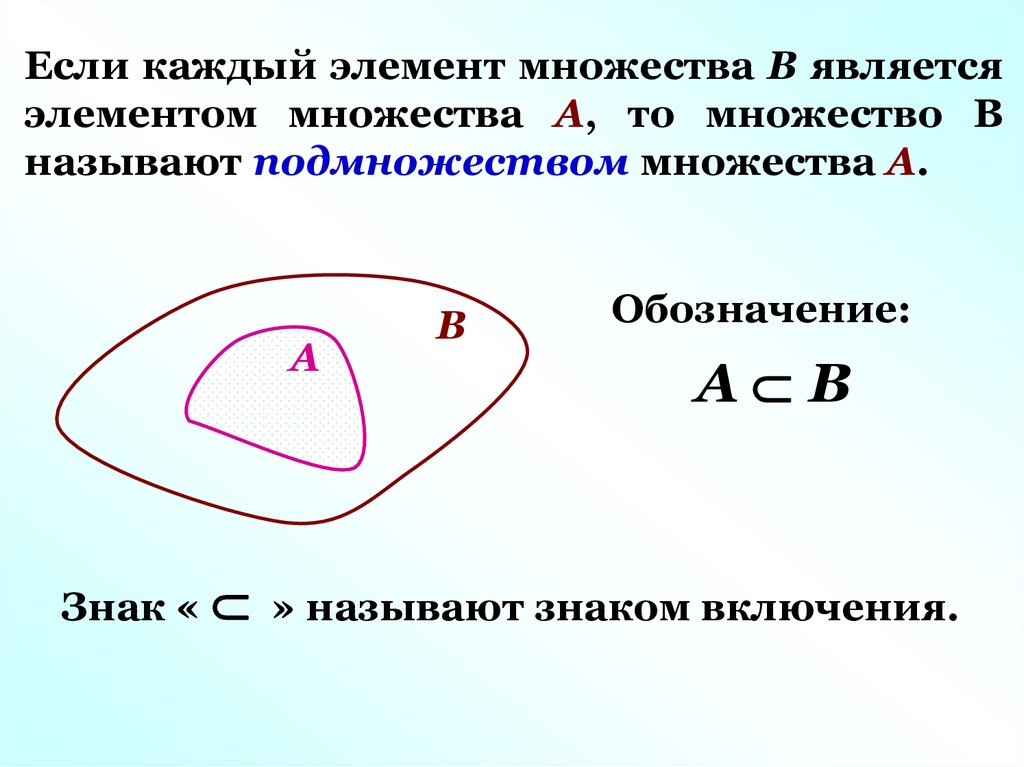
Если каждый элемент множества В являетсяэлементом множества А, то множество В
называют подмножеством множества А.
А
В
Обозначение:
А В
Знак « » называют знаком включения.
4.
№ 1127 Даны два множества. При по мощи знаковзапишите, как эти множества связаны друг с
другом, если это возможно.
а) А – множество всех треугольников, В – множество многоугольников, имеющих три стороны
и три угла;
А=В
б) С – множество всех четырёхугольников, D – множество всех треугольников;
невозможно
5.
№ 1127 Даны два множества. При по мощи знаковзапишите, как эти множества связаны друг с
другом, если это возможно.
в) Е – множество окружностей, F – множество
кругов;
E F
г) G – множество всех треугольников, H – множество замкнутых ломаных, имеющих три звена.
H G
6.
32
5
3
2
1
1
=5
1) 3 +2 = 3 + 2
12
12
12
4
6
5
65 13 65 5 25
=
2)
:
=
12 5 12 13 12
6
2
3
2 9 3
3) =
3 4 2
2
25 3 31 25 18 62 69 23
3
4)
+
=
+
=
=
=5
12 2 6
12 12 12 12 4
4
7.
16.06.2019К л а с с н а я р а б о т а.
8.
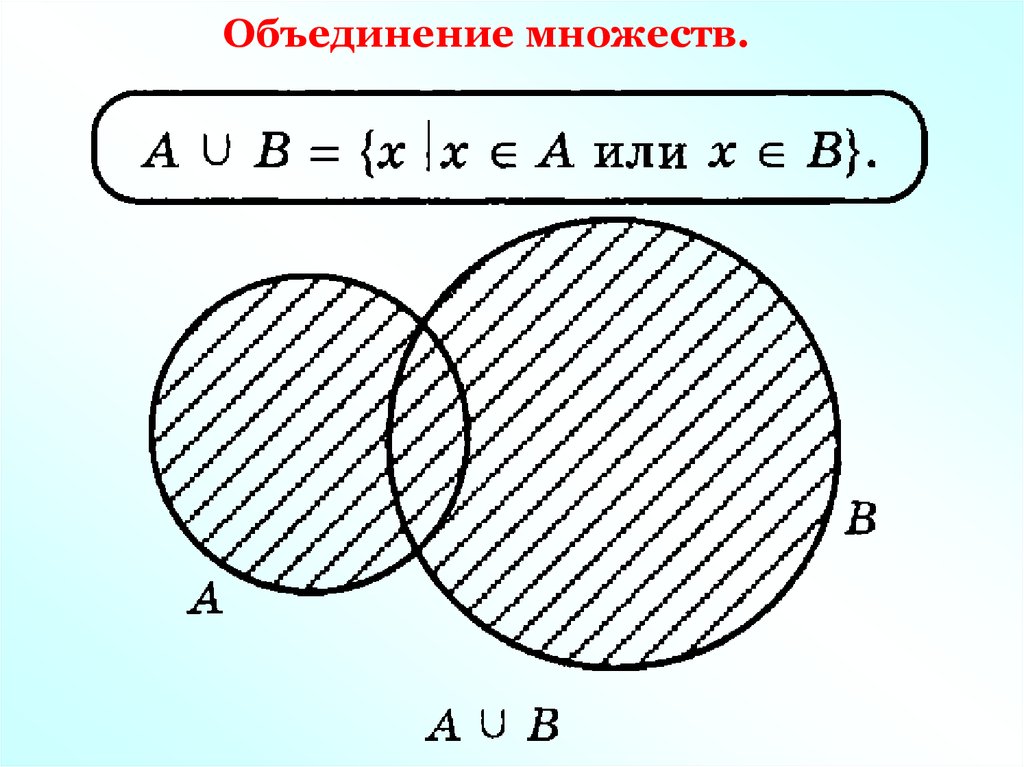
Объединение множеств.Рассмотрим два множества:
А = {1, 2, 3, 4, 5, 6} и В = {5, 6, 7, 8, 9}.
Составьте новое множество D, которое содержит все элементы, которые принадлежат хотя бы одному множеству А или В.
D = {1, 2, 3, 4, 5, 6, 7, 8, 9}
Множество D является объединением множеств А и В, и обозначается так
А В=D
Объединением двух множеств называют множество, состоящее из всех элементов, принадлежащих
хотя бы одному из этих множеств.
9.
Объединение множеств.10.
Объединение множеств.11.
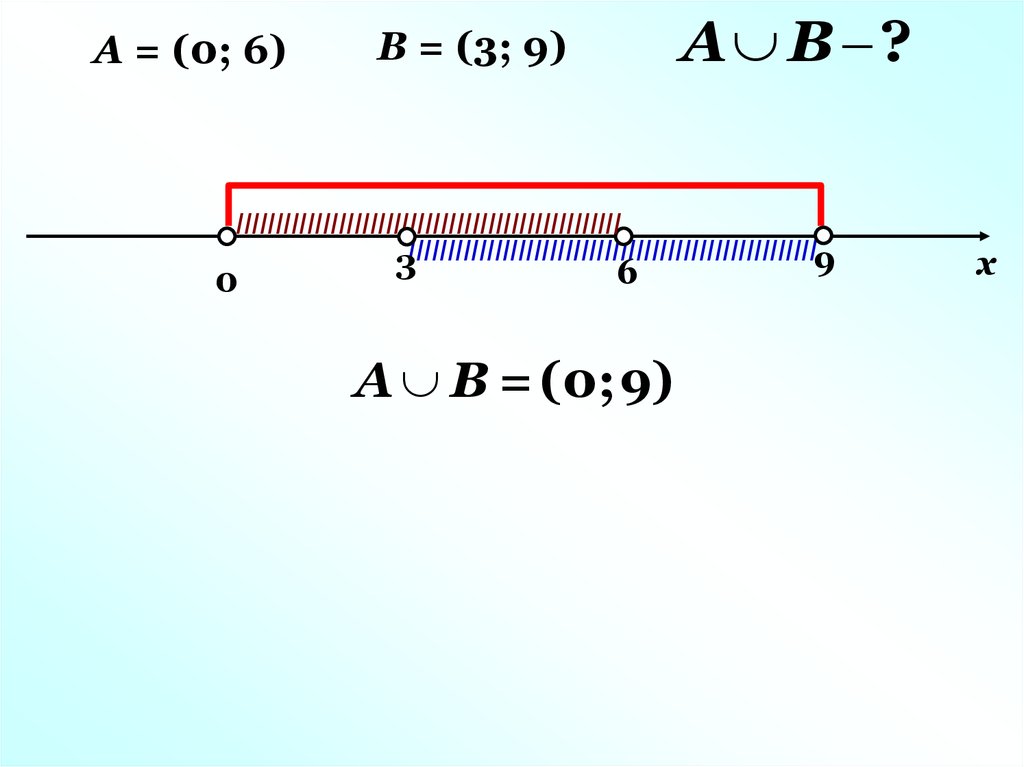
А = (0; 6)А В ?
В = (3; 9)
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0
3
6
А В = (0;9)
9
х
12.
Запись десятичной дроби в видеобыкновенной
7
0,7 =
10
4 2
0,4 =
=
10 5
5
29
05
=3
3,05 = 3
1,29 = 1
100
100
100
1
025
10,025 = 10
= 10
40
1000
13.
Запись обыкновенной дроби ввиде десятичной (1 способ)
3
= 0,003
1000
5
1 5
=
= 0,5
2 10
25
75
3
= 0,75
=
4 100
125
125
1
= 0,125
=
8 1000
4
28
7
= 0,28
=
25 100
2
14
7
= 3,14
3
=3
100
50
14.
Запись обыкновенной дроби ввиде десятичной (2 способ)
741
= 1,14
650
741,00 650
1, 1 4
650
91
650
260
2600
0
15.
У: № 1130; 1091;1094(в).











 Математика
Математика








