Похожие презентации:
ВКР: Математическое и программное обеспечение для исследования простых эвристик при решении задач линейного раскроя
1. Уфимский государственный авиационный технический университет
Математическое и программное обеспечениедля исследования простых эвристик при
решении задач линейного раскроя
Зозуленко А.С., ст.гр. ПРО-410
руководитель:
Валеева А.Ф.
2.
2Цель работы:
»
Сравнение эффективности различных алгоритмов
для решения разных классов задач линейного раскроя
на основе вычислительного эксперимента.
» Задачи:
• выполнить аналитический обзор методов решения
целочисленных задач линейного раскроя;
• реализовать в виде программного продукта
алгоритмы линейного раскроя на базе метода простых
эвристик;
• провести вычислительный эксперимент для
исследования влияния исходных данных на результат
решения задачи линейного раскроя;
• разработать рекомендации по выбору алгоритма в
зависимости от исходных данных.
3.
US E D A T :A UT HOR:
DA T E :22.01.2016
W ORK ING
RE V : 15.06.2016
DRA FT
ПОСТАНОВКА
ЗАДАЧИ
P ROJ E CT: Linear
RE A DE R
3
TOP
RE COMMENDE D
NOT E S : 1 2 3 4 5 6 7 8 9 10
DA T E CONT E X T:
P UB LICA TION
Начальные условия и
ограничения задачи
линейного раскроя
Параметры
набора исходных
данных
Иссл е дование эффективности
простых эвристик при ре ше нии
задач лине йного раскроя
Р екомендации по выбору
алгоритма
A0
Лицо,
принимающее
решение
Методы
раскроя
Программнотехнические средства
4.
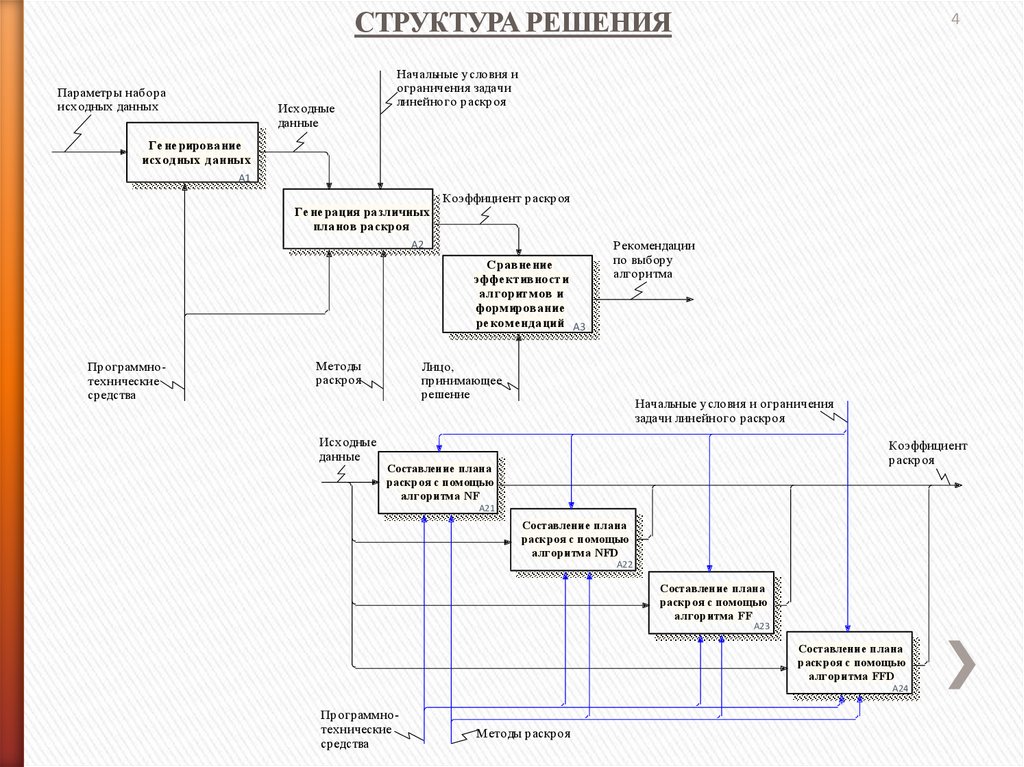
US E D A T :СТРУКТУРА РЕШЕНИЯ
A UT HOR:
DA T E : 22.01.2016
W ORK ING
P ROJ E CT: Linear
RE V : 13.06.2016
DRA FT
RE A DE R
4
DA T E CONT E X T:
RE COMMENDE D
NOT E S : 1 2 3 4 5 6 7 8 9 10
P UB LICA TION
Параметры набора
исходных данных
Исходные
данные
A -0
Начальные условия и
ограничения задачи
линейного раскроя
Ге не рирование
исходных данных
A1
Коэффициент раскроя
Ге не рация разл ичных
пл анов раскроя
A2
С равнение
эффе ктивности
ал горитмов и
формирование
ре комендаций A3
US E D A T :
Методы
раскроя
Программнотехнические
средства
NODE :
A UT HOR:
DA T E :29.05.2016
W ORK ING
P ROJ E CT: Linear
RE V : 14.06.2016
DRA FT
Лицо,
P UB LICA TION
Èññëåäîâàíèå ýôôåêòèâíîñòè ïðîñòûõ ýâðèñòèê ïðè
ðåøåíèè äåêîìïîçèöèè
çàäà÷ ëèíåéíîãî ðàñêðîÿ
Исходные
данные
RE A DE R
DA T E CONT E X T:
RE COMMENDE D
NOT E S : 1 2принимающее
3 4 5 6 7 8 9 10
решение
T IT LE :
A0
Р екомендации
по выбору
алгоритма
A0
Начальные условия и ограничения
задачи линейного раскроя
NUMB E R:
Коэффициент
раскроя
Составление плана
раскроя с помощью
алгоритма NF
A21
Составление плана
раскроя с помощью
алгоритма NFD
A22
Составление плана
раскроя с помощью
алгоритма FF
A23
Составление плана
раскроя с помощью
алгоритма FFD
A24
Программнотехнические
средства
NODE :
Методы раскроя
T IT LE :
NUMB E R:
5.
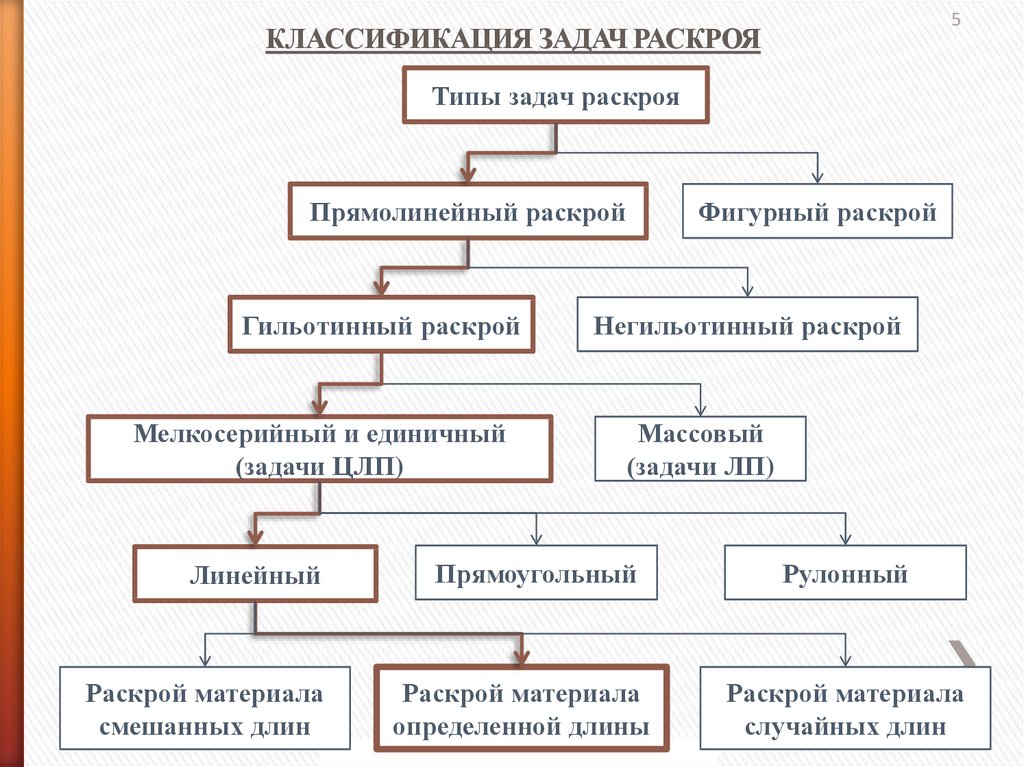
5КЛАССИФИКАЦИЯ ЗАДАЧ РАСКРОЯ
Типы задач раскроя
Прямолинейный раскрой
Гильотинный раскрой
Мелкосерийный и единичный
(задачи ЦЛП)
Линейный
Раскрой материала
смешанных длин
Фигурный раскрой
Негильотинный раскрой
Массовый
(задачи ЛП)
Прямоугольный
Раскрой материала
определенной длины
Рулонный
Раскрой материала
случайных длин
6.
ЗАДАЧА ЛИНЕЙНОГО РАСКРОЯ В УСЛОВИЯХ ЕДИНИЧНОГО(МЕЛКОСЕРИЙНОГО) ПРОИЗВОДСТВА
»
6
ПОСТАНОВКА ЗАДАЧИ
Дано:
• набор стержней длины L;
• комплект требуемых заготовок W = {1, … , m} , где
»
m – количество заготовок;
» li – длина i-й заготовки, li (0,L), i (1..m);
» bi - необходимое количество каждой заготовки i (1..m);
» Найти:
»
Рациональный план раскроя, который включает в себя:
»
– r1,r2,…,rp – совокупность способов раскроев;
»
– x1,x2,…,xp – вектор интенсивностей способов раскроев, где xj – количество единиц
материала, раскраиваемого по способу rj , j ∈ 1, p .
»
Произвести раскрой заготовок, минимизируя отходы.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Рассматриваемая задача раскроя сводится к следующей целочисленной модели линейного
программирования:
При заданных целых параметрах заготовок











 Информатика
Информатика








