Усвоение соответствий понятий о свойствах функции и её производной. Открытый банк заданий ЕГЭ

1.

8
Соловьёв Леонид Максимович,
Соловьёва Галина Николаевна,
учителя математики МОУ «СОШ № 3»
г. Анжеро-Судженск Кемеровской области 2011г.
Открытый банк
заданий ЕГЭ
по математике
(http://mathege.ru/or/ege/Main)
«Мой университет- www. moi-mummi.ru»

2.

Цель: Осознанное усвоение
соответствий понятий
о свойствах функции
и её производной.
Не отвлекайтесь !

3.

3
Что
Свойства
можнофункции
сказать
«Вграфику
поход»
очитаем
производной
по
f’(x) ?
«Человек из дома вышел,
Посмотреть на мир поближе»…
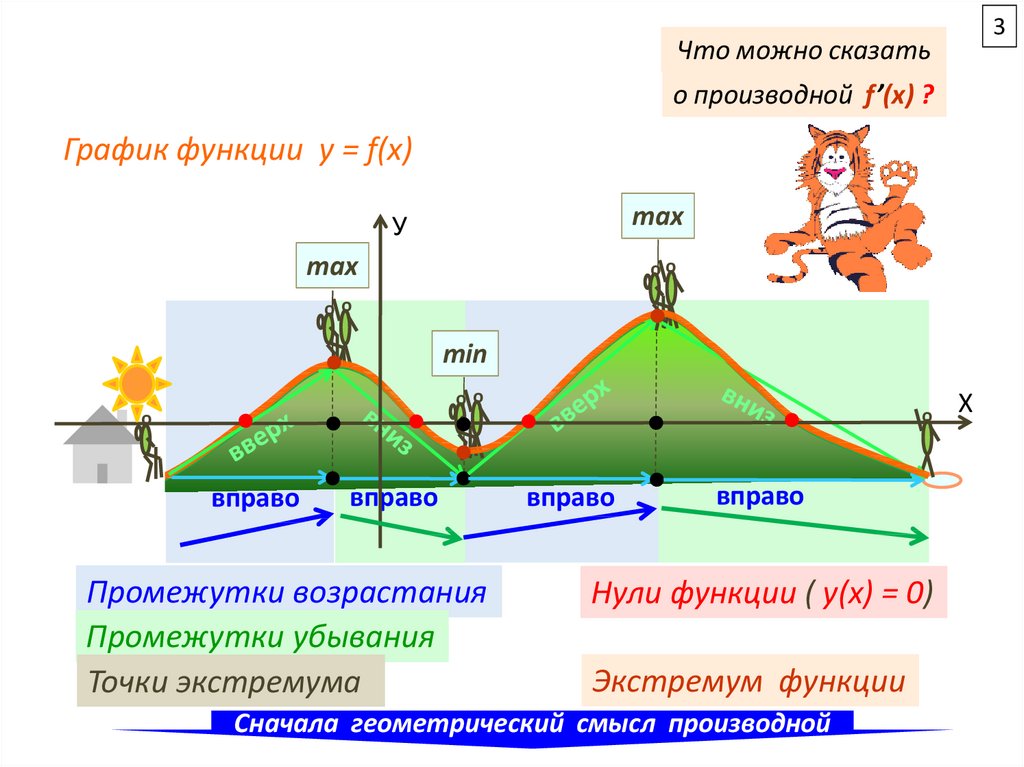
График
функции
y = f(x)
(по горам,
по долам…)
max
У
max
оо
оо
о
вправо
min
оо
•
• вправо
Промежутки возрастания
Промежутки убывания
Точки экстремума
вправо
о
вправо
Нули функции ( у(х) = 0)
Экстремум функции
Сначала геометрический смысл производной
Х

4.

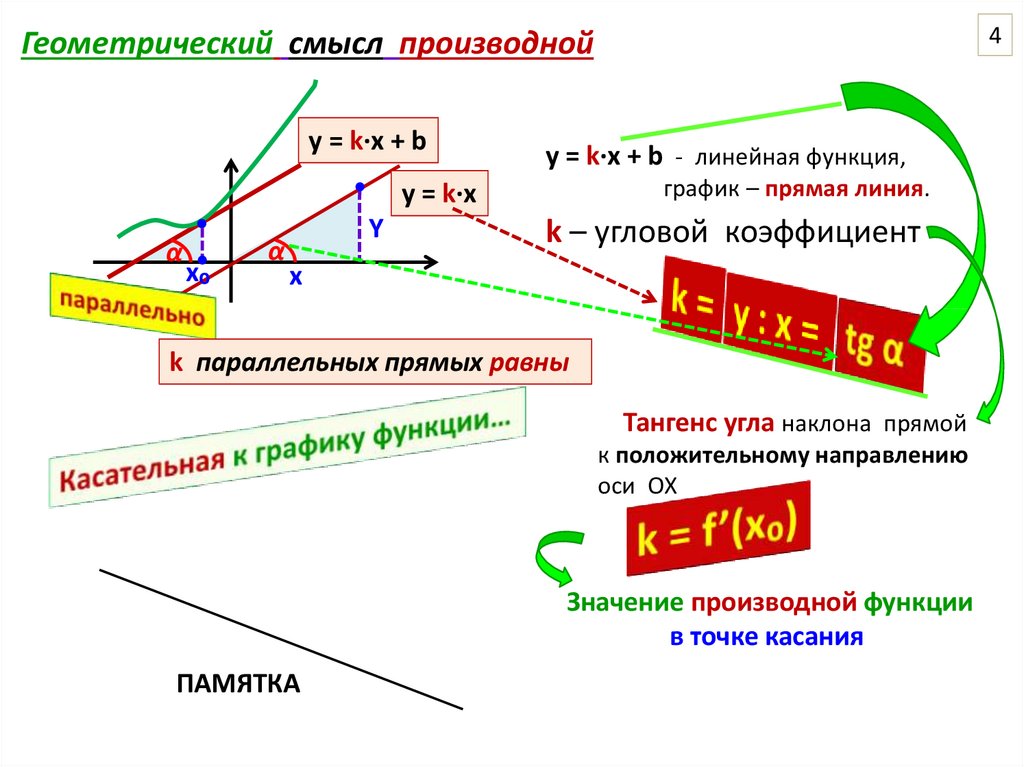
4
Геометрический смысл производной
у = k∙x + b
α
x₀
α
у = k∙x + b - линейная функция,
график – прямая линия.
у = k∙x
Y
k – угловой коэффициент
x
k параллельных прямых равны
Тангенс угла наклона прямой
к положительному направлению
оси ОХ
Значение производной функции
в точке касания
ПАМЯТКА

5.

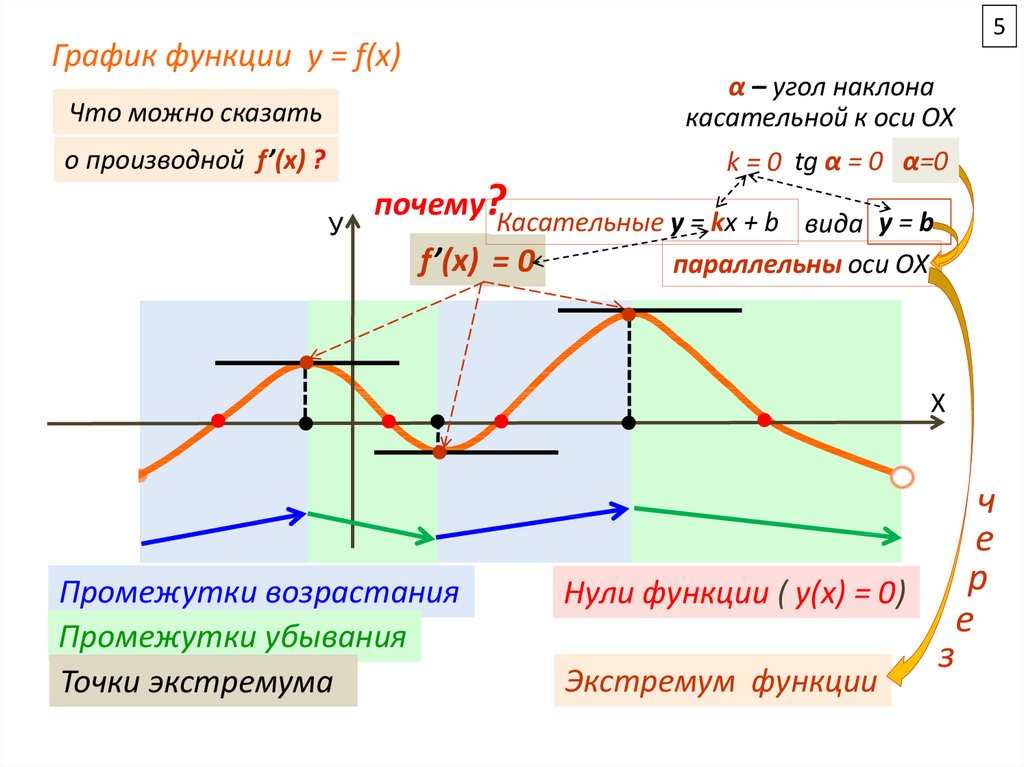
5
График функции y = f(x)
Что можно сказать
α – угол наклона
касательной к оси ОХ
о производной f’(x) ?
k = 0 tg α = 0 α=0
У
почему?Касательные y = kx + b
вида y = b
параллельны оси ОХ
f’(x) = 0
•
Промежутки возрастания
Промежутки убывания
Точки экстремума
Х
Нули функции ( у(х) = 0)
Экстремум функции
з
ч
е
р
е

6.

6
График функции y = f(x)
k = tgα > 0
k = tgα < 0
Что можно сказать
о производной f’(x) ?
Касательные y = kx + b
Углы наклона ОСТРЫЕ
Касательные y = kx + b
Углы наклона ТУПЫЕ
У
Почему ?
f’(x) > 0
Почему ?
f’(x) < 0
/////////////////
///////////////////
////////////////////////////
//////////////
•
Промежутки возрастания
Промежутки убывания
Точки экстремума
Нули функции ( у(х) = 0)
Экстремумы функции
Х

7.

7
по
по графику
графику
В 8.
(2012) На рисунке изображён график функции y=f(x)
отмечены восемь точек на оси абсцисс: х₁ , х₂ , … х₈.
Две задачи
?
В скольких из этих точек производная функции f(x)
отрицательна ? (1)
Y
Решение: f(x)
Решение:
положительна ? (2)
возрастает
убывает
•
Х₁ Х₂
?
Х₄
••
Х₅
Х₃
0
Х₆
Х₇
•Х₈
X
Ответ: 2
Ответ: 4
Почему
не берём точки
Х₂ и Х₇ ? Х₂ и Х₇ - точки
экстремума.
Дополнительный
вопрос
Ответ
f’(Х)
=0!
В них

8.

График функции y = f(x)
8
Что можно сказать
о производной f’(x) ?
Значение производной
б) указаны
не указаны
в точке касания (по рис.) а)
дветочки
точкипрямой
прямой САМИ укажем !
У
(2)
(2)
4
y = f(x)
(1)
x₀• π–α
α
(1)
f’(x) = tg (π–α) =
5
= - tgα = – 4:5 = – 0,8
α
3
•х₀
Х
4
f’(x) = tg α = 3:4= 0,75
Через точку (1), которая НИЖЕ - прямую параллельно ОХ
Как и в 1-м случае
Через точку (2), которая ВЫШЕ - прямую параллельно ОУ

9.

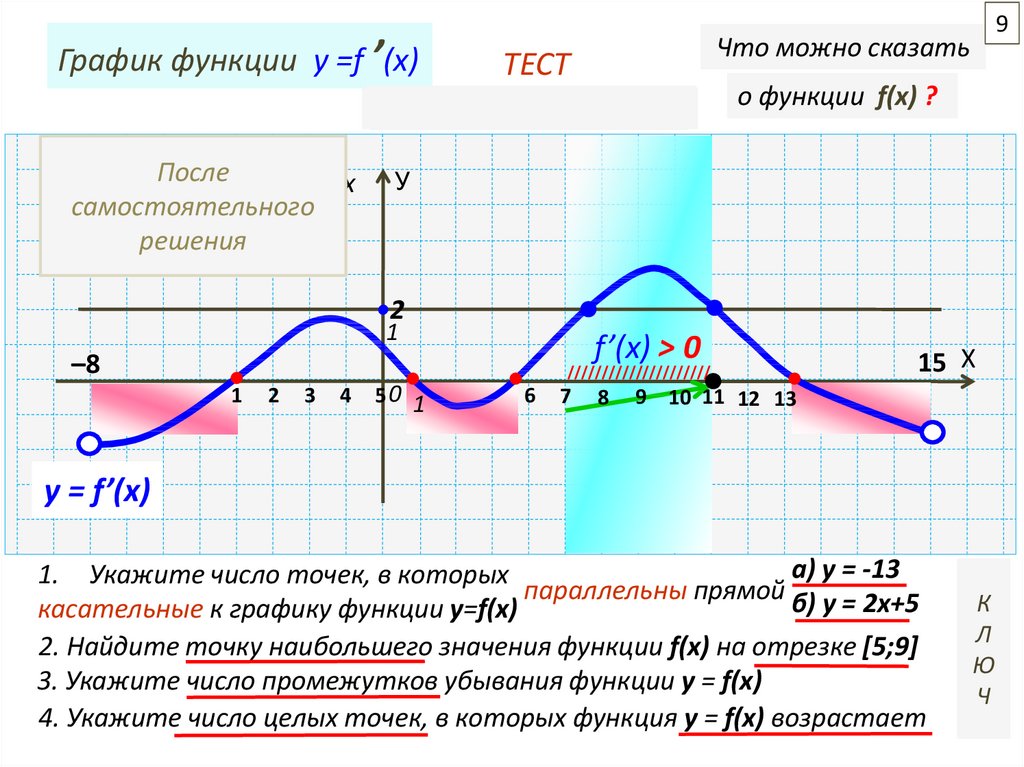
График функции y =f ’(x)
Что можно сказать
ТЕСТ
о функции f(x) ?
сверить
свои
рассуждения
Ответить
на
все вопросы
проверить,
кликнув
ключ
График
f’(x) у=2х+5
2.
4.
3.Это
абсциссы
точек
Дана
прямая
1б.
1а.
-После
убывает
-ОХ
касательная
y=
k=2
уf(X)
всех
параллельных
выше
осиkx+b
промежутков
на
промежутках,
самостоятельного
данная
y=0x-13
f’(x)(f’(x)
= 2 где
прямых
возрастания
≥ 0)
f(x) -прямая
возрастает
решения
f’(x)
f’(x)
= k≤
=00
f(9)
- наибольшее
целые
числа
У
•2
1
–8
•1
2
3
4
50 1
•6
f’(x) > 0
/////////////////////
7
8
15 Х
9 10 11 12 13
y = f’(x)
а) у = -13
1. Укажите число точек, в которых
параллельны прямой б) у = 2х+5
касательные к графику функции у=f(x)
2. Найдите точку наибольшего значения функции f(x) на отрезке [5;9]
3. Укажите число промежутков убывания функции y = f(x)
4. Укажите число целых точек, в которых функция y = f(x) возрастает
4
2К
9Л
Ю
3Ч
13
9

10.

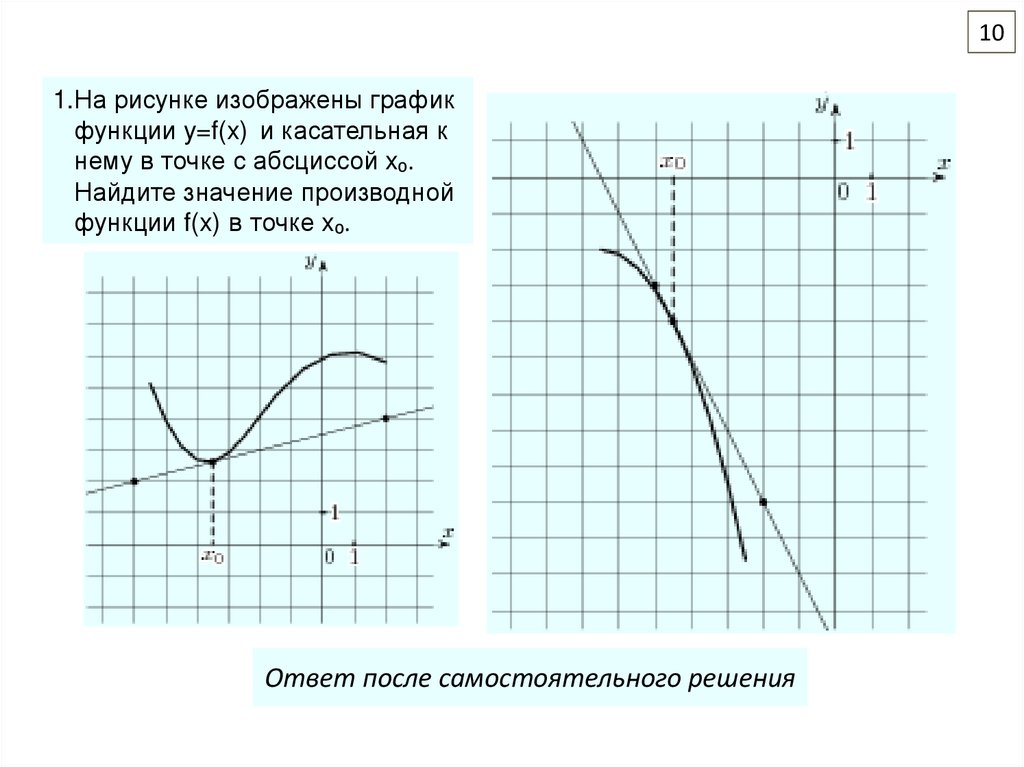
10
1.На рисунке изображены график
функции y=f(x) и касательная к
нему в точке с абсциссой x₀.
Найдите значение производной
функции f(x) в точке x₀.
6
2
α
tg = 0,25
8
угол
треугольник
Через уровнем
ниже
выше
π–α
α
3
tg (π–α) = −tg α = - 6 :3 =-2
0,25самостоятельного
Ответ после
решения
–2

11.

11
Ответ после
18 самостоятельного
- 7 решения
f’(x) ≤ 0
f(x) убывает
/////////////////////////////
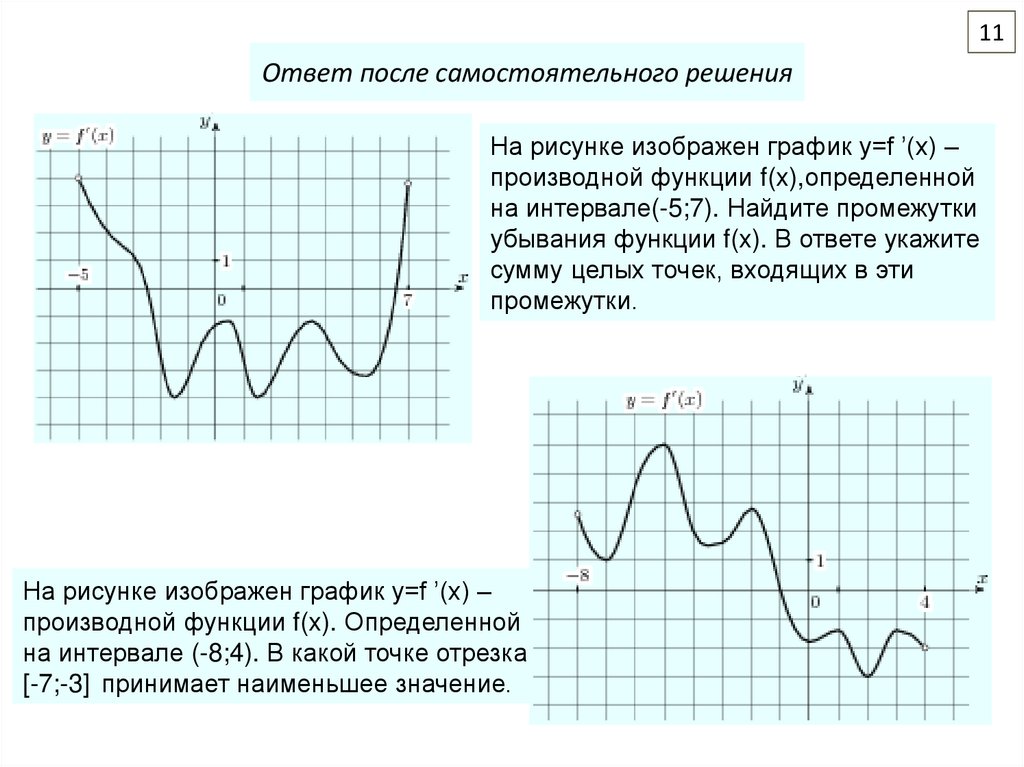
На рисунке изображен график y=f ’(x) –
производной функции f(x),определенной
на интервале(-5;7). Найдите промежутки
убывания функции f(x). В ответе укажите
сумму целых точек, входящих в эти
промежутки.
Целые
точки
-2 -1 +0 +1+2+3 +4 +5+6 = 18
На рисунке изображен график y=f ’(x) –
производной функции f(x). Определенной
на интервале (-8;4). В какой точке отрезка
[-7;-3] принимает наименьшее значение.
/////////////
Почему ? f’(x)>0
И что ?
-7

12.

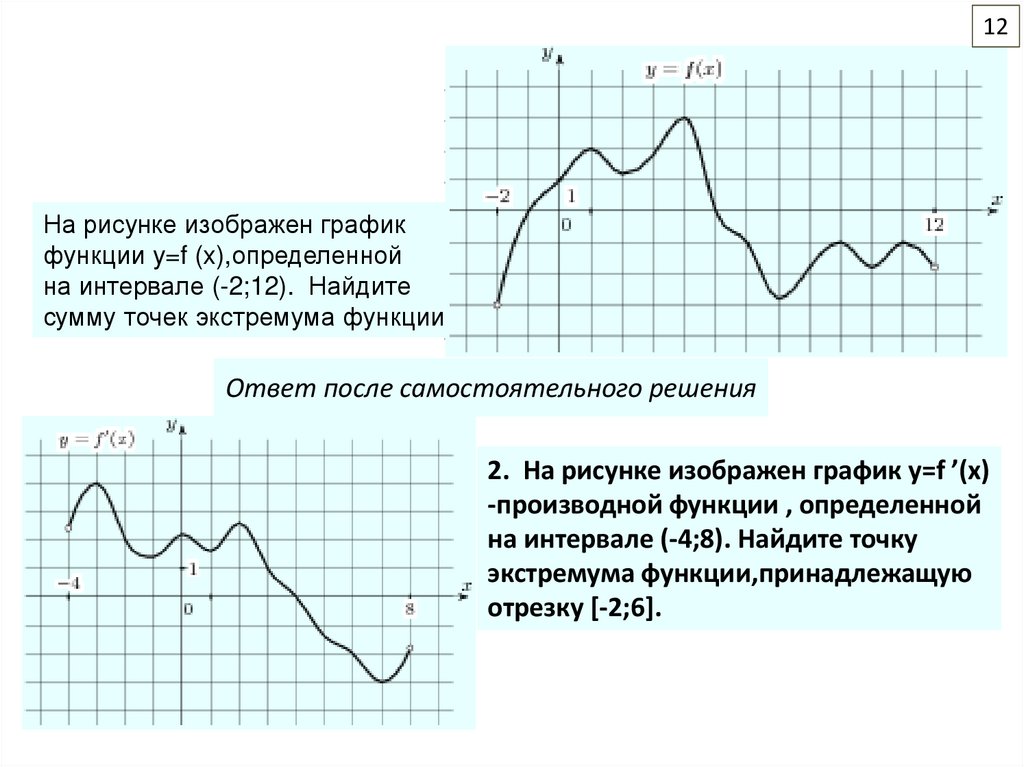
12
На рисунке изображен график
функции y=f (x),определенной
на интервале (-2;12). Найдите
сумму точек экстремума функции.
• экстремум функции
f’(x) = 0
1 +2
+4
+7
+9 +10 +11 = 44
Ответ
4
44 после самостоятельного решения
Точка экстремума
f’(x) = 0
−2
4
6
2. На рисунке изображен график y=f ’(x)
-производной функции , определенной
на интервале (-4;8). Найдите точку
экстремума функции,принадлежащую
отрезку [-2;6].

13.

13
−0, 6
ответ
решение
10
6
π−α
α
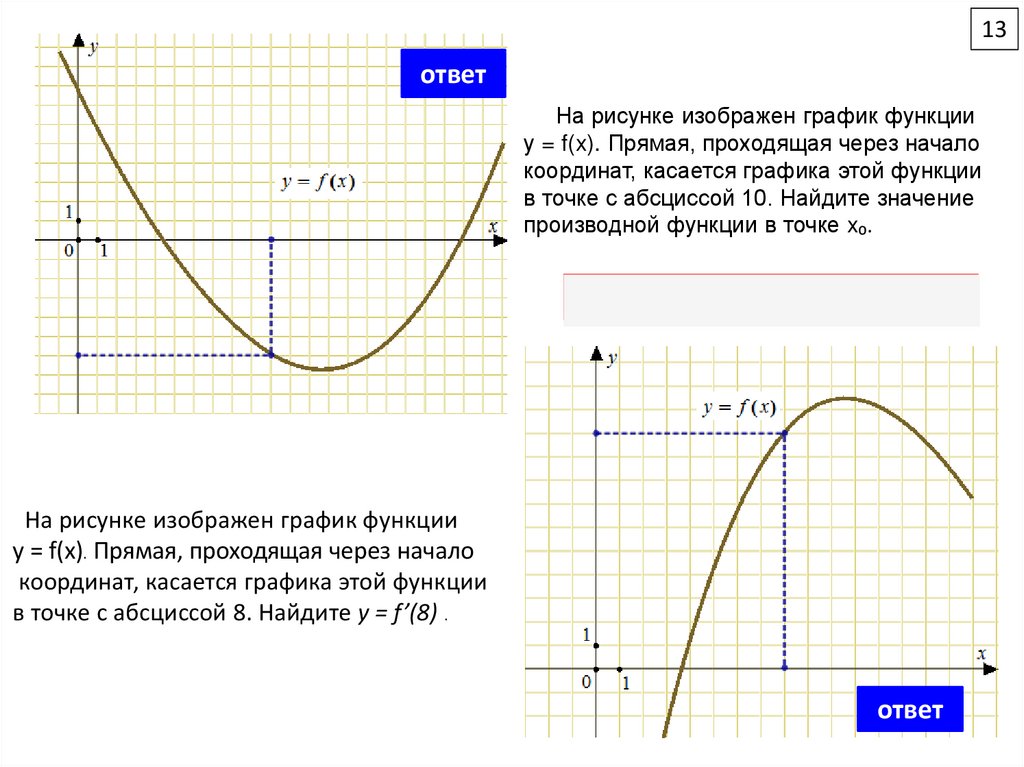
На рисунке изображен график функции
у = f(x). Прямая, проходящая через начало
координат, касается графика этой функции
в точке с абсциссой 10. Найдите значение
производной функции в точке x₀.
Сами
проводили
касательную!
В чём
особенность
задач?
10
f’(x₀) = tg(π−α) = −tgα = − 6 : 10
На рисунке изображен график функции
y = f(x). Прямая, проходящая через начало
координат, касается графика этой функции
в точке с абсциссой 8. Найдите y = f’(8) .
Решение:
10
tgα = 10:8 = 1,25 = f’(x₀)
α
8
ответ
1,25

14.

14
Используемые ресурсы
Открытый банк задач ЕГЭ по математике
http://mathege.ru/or/ege/Main
В8. Прототипы заданий
http://mathege.ru/or/ege/ShowProblems.html
?posMask=128&showProto=true
http://miranimashek.com/index/0-92
http://smayli.ru/koshkia_8.html
http://smayli.ru/jivotniea_10.html
«Мой университет- www. moi-mummi.ru»