Системы линейных уравнений с двумя переменными. 7 класс

1. Системы линейных уравнений с двумя переменными

Учитель:
Полякова
Ольга Васильевна
МОУ «СОШ №8»
г. Новомосковск

2. Цели урока:

Повторить алгоритм решения систем уравнений
графическим методом, методом подстановки и
сложения, рассмотреть применение систем как
модели реальных ситуаций.

3. Угадайте, о какой функции идёт речь?

А я бесхитростна, проста –
Такой характер у меня.
Смеются надо мной друзья:
Мол, нет извилин у меня.
Но я с дороги не сверну,
Ведь жить иначе не могу”.
Прямая
у
5
4
3
2
1
у
0
-4
-3
-2
-1
-1
-2
-3
0
1
2
3
4
х

4.

Математический бильярд
2
1
4
3

5.

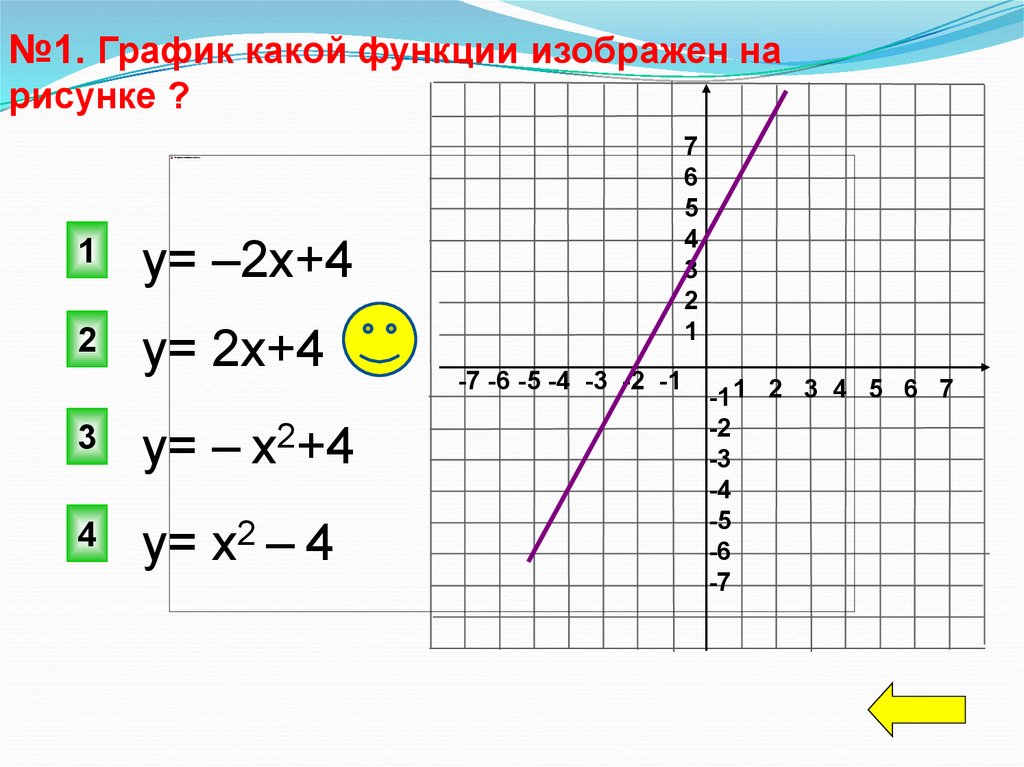
№1. График какой функции изображен на
рисунке ?
1
у= –2х+4
2
у= 2х+4
3
у= – х2+4
4
у= х2 – 4
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
-1 1 2 3 4 5 6 7
-2
-3
-4
-5
-6
-7

6.

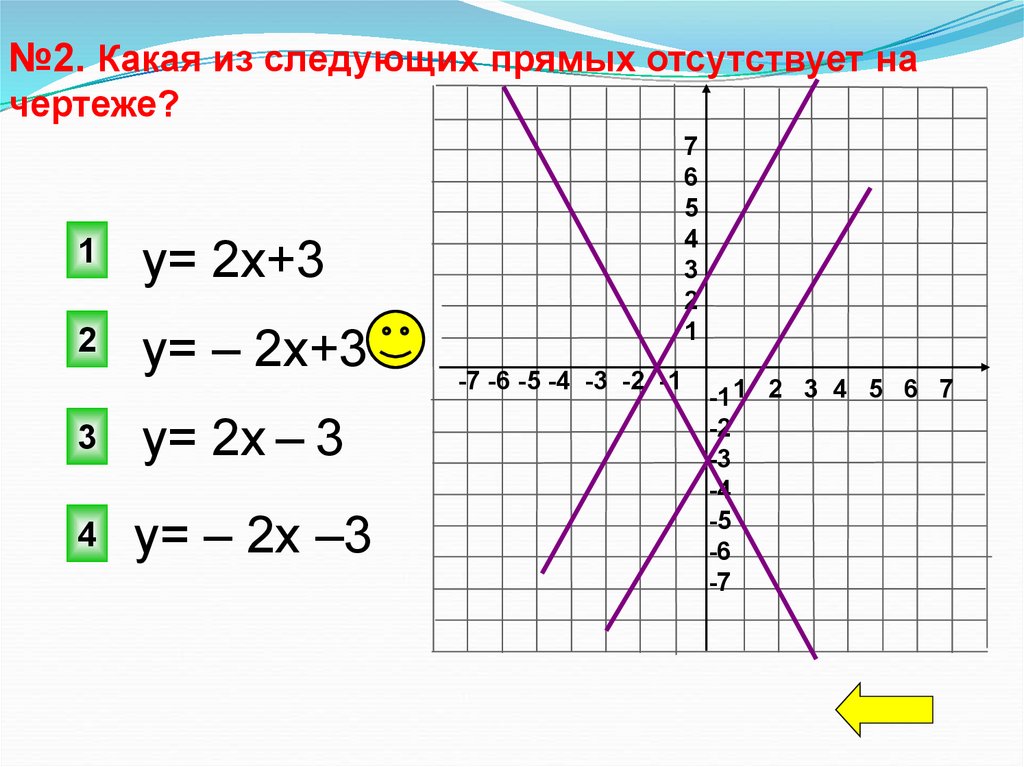
№2. Какая из следующих прямых отсутствует на
чертеже?
1
у= 2х+3
2
у= – 2х+3
3
у= 2х – 3
4
у= – 2х –3
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
-1 1 2 3 4 5 6 7
-2
-3
-4
-5
-6
-7

7.

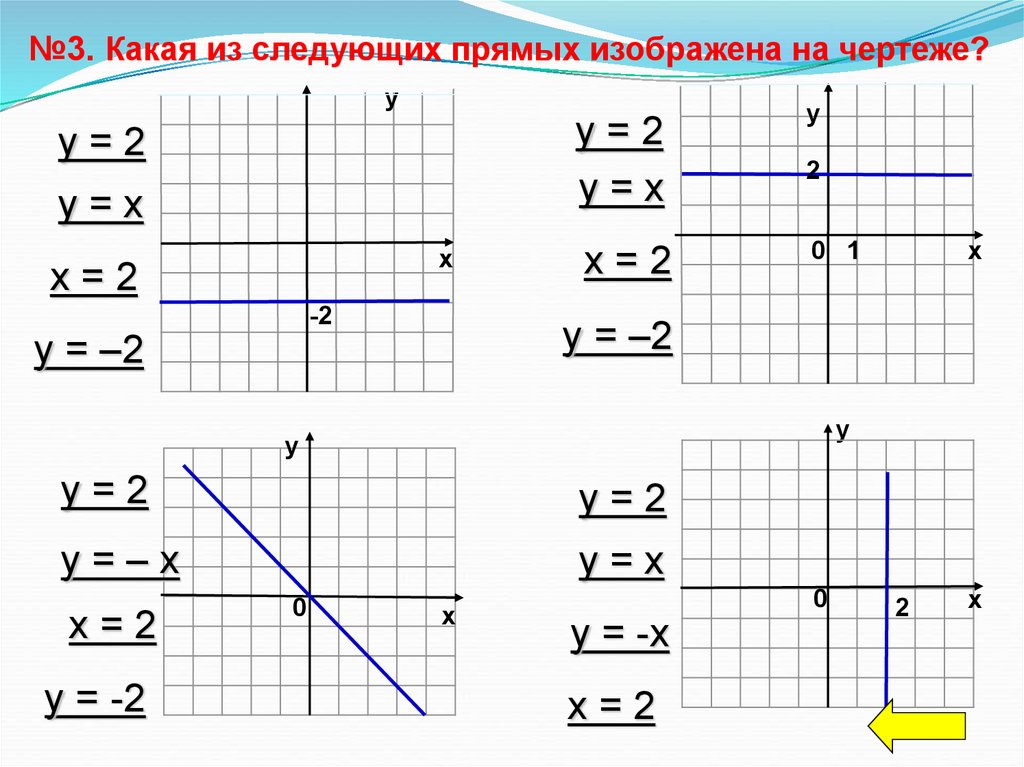
№3. Какая из следующих прямых изображена на чертеже?
у
у=2
у=х
у=2
у=х
х
х=2
-2
у = –2
х=2
у
2
у = –2
у
у
у=2
у=2
у=–х
у=х
х=2
у = -2
0
х
0 1
х
у = -х
х=2
0
2
х

8.

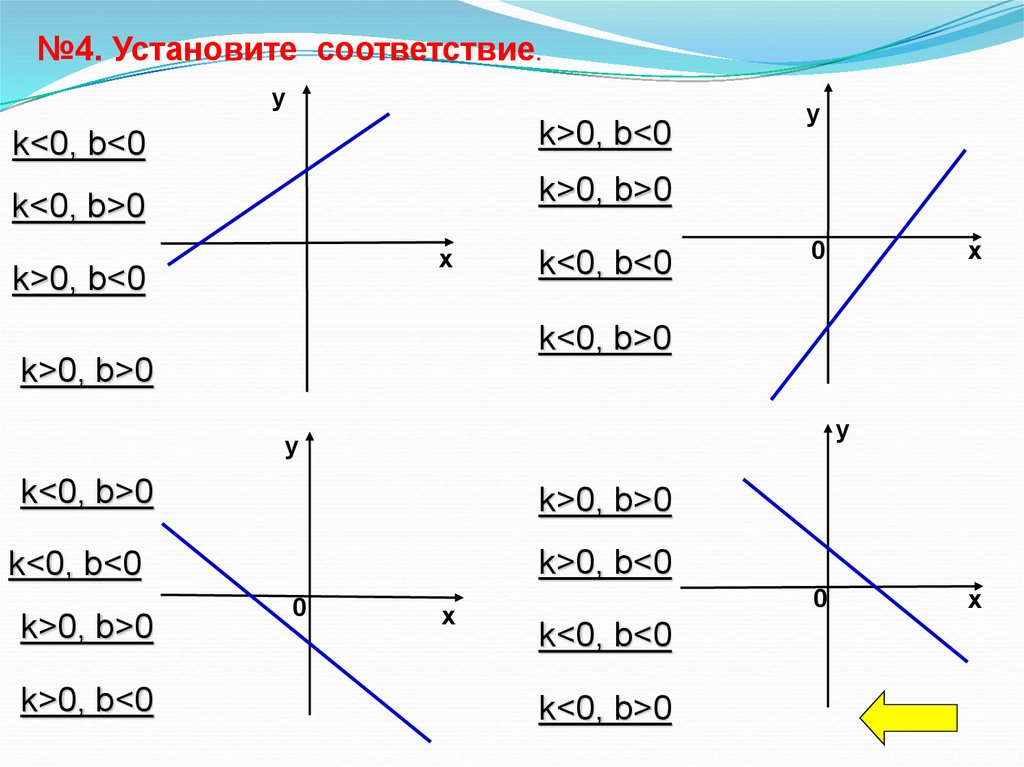
№4. Установите соответствие.
у
k<0, b<0
k>0, b<0
k<0, b>0
k>0, b>0
х
k>0, b<0
k<0, b<0
у
х
0
k<0, b>0
k>0, b>0
у
у
k<0, b>0
k>0, b>0
k>0, b<0
k<0, b<0
k>0, b>0
k>0, b<0
0
х
0
k<0, b<0
k<0, b>0
х

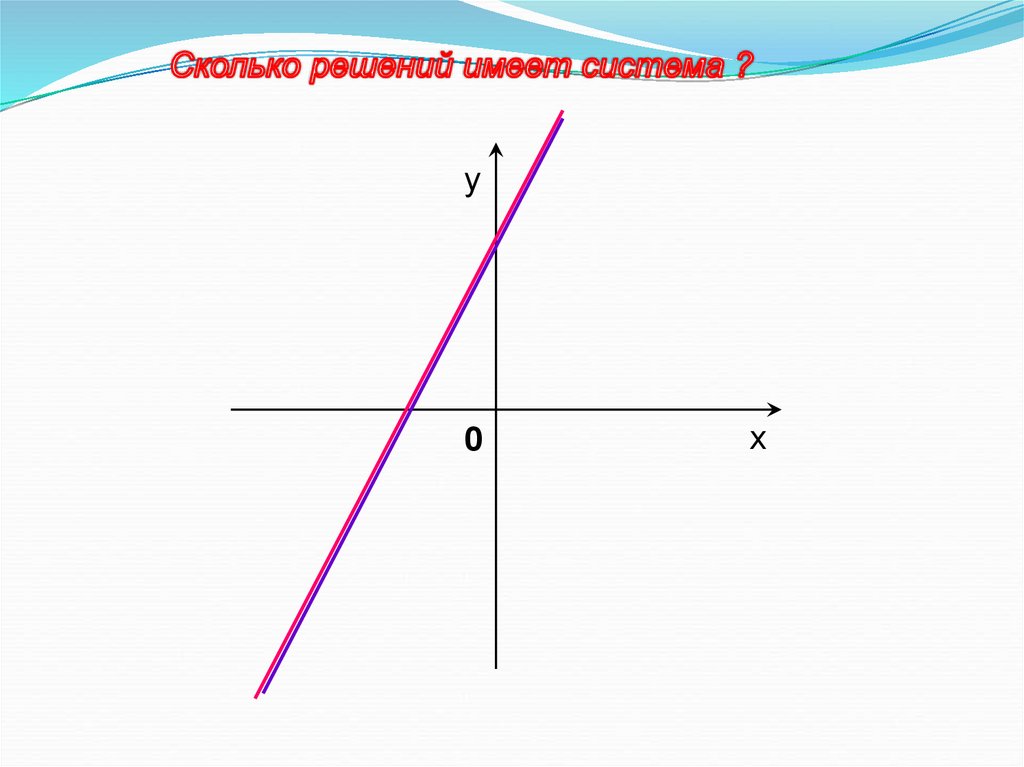
9.

10.

у
0
х

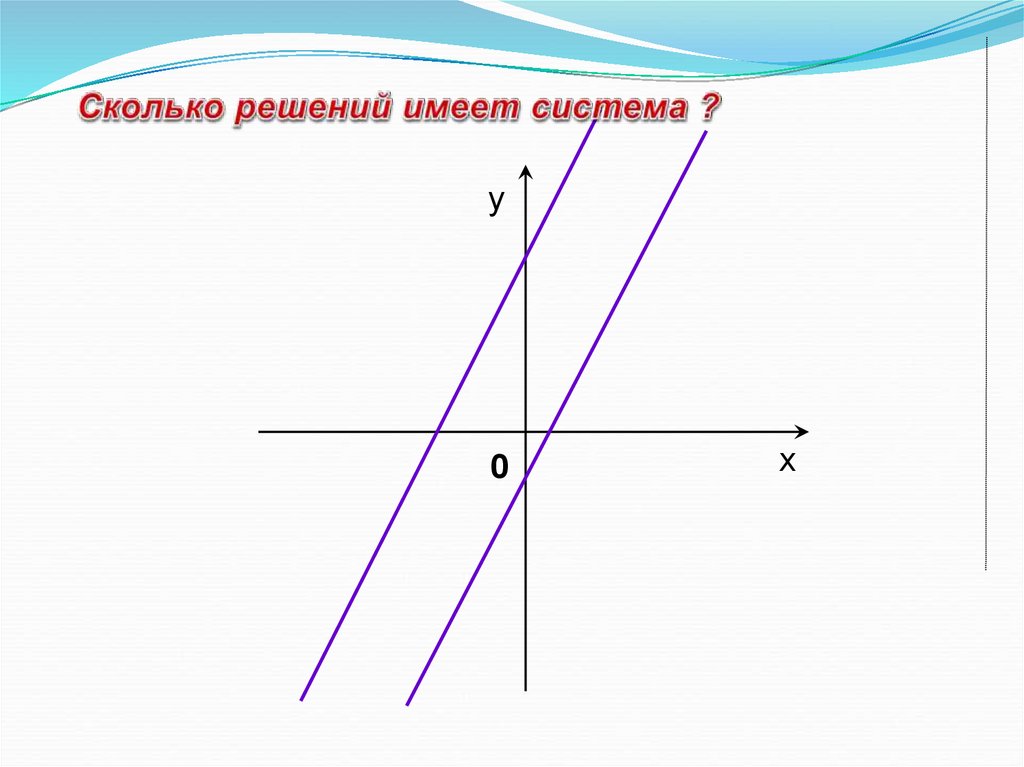
11.

у
0
х

12. Подберите такое значение k, при котором система

Имеет единственное
решение
У= 3х – 5
У= kх + 4
Не имеет решений
У =5х
У =kх - 7

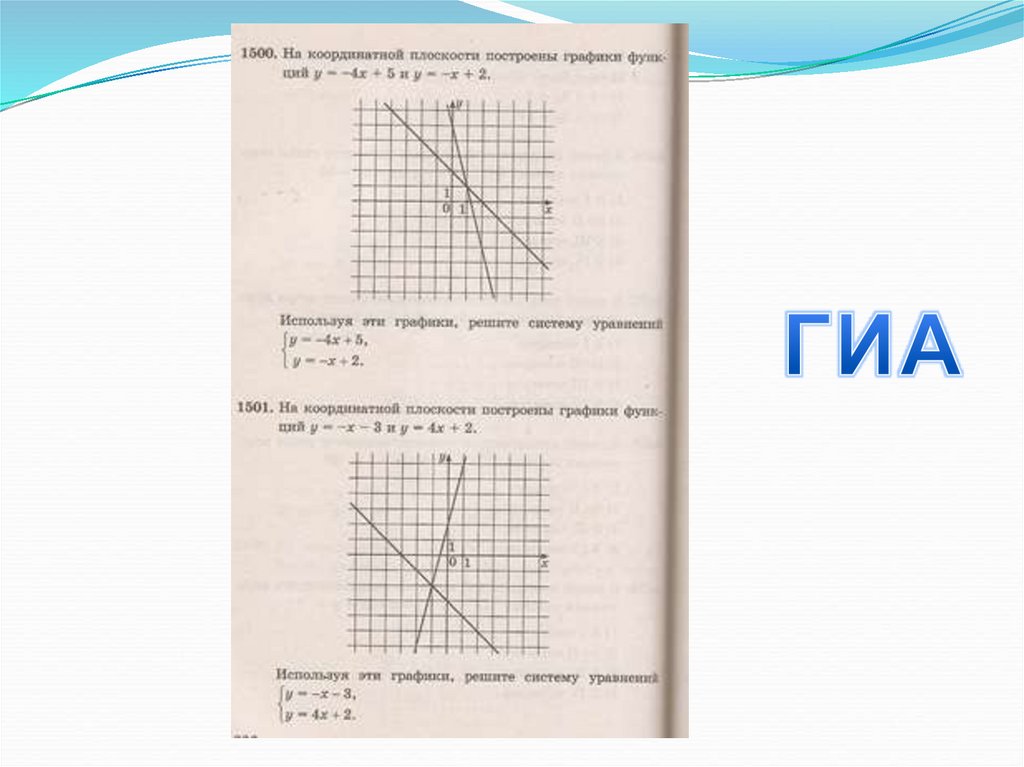
13. Задание

Решить систему графически:
У = 3х-4
У = -х+4
Задание

14. Решить систему методом сложения(1в), подстановки(2в).

1 вариант
х+у=7
2х - у = 8
2 вариант
х 2 у 3х у
5
5
3
2 х 3 у 1

15. Решение системы 2 варианта:

х 2 у 3х у
5
3
2 х 3 у 1
5
3(х+2у)+5(3х-у)=75
2х – 3у =-1
3х+6у+15х-5у=75
2х – 3у =-1
18х+у =75
2х – 3у =-1
у=75-18х
2х-3(75-18х)=-1
2х-225+54х=-1
56х=224
х=4
х=4
у=3 Ответ:(4;3)

16. Решение системы 1 варианта

Ответ: (5;2).

17. Решите задачу.

Вариант
1
Задумали два числа. Одно
число больше другого на 10.
а их сумма равна 140.
Найдите эти числа.
2
Вариант .
За 4 часа езды на
автомобиле и 7 часов езды
на поезде туристы проехали
640 км. Какова скорость
поезда, если она на 5 км/ч
больше скорости
автомобиля?

18. Решение задач .

Вариант
1
Вариант 2
4x+7x+35=640
11x=605
x=55
Ответ: одно число 65,
второе 75.
Ответ: скорость поезда
60 км/ч.

19. Домашнее задание.

Дидактические материалы.
К-10А. По вариантам 1-2.