Применение производной для решения.11 класс

1. Применение производной для решения задач урок алгебры, 11 класс

2. Три пути ведут к знанию: - путь размышления – это путь самый благородный, - путь подражания – это путь самый легкий и путь

опыта – это путь самый
горький.
Конфуций

3.

1) Даны графики функций и графики производных. Для каждой из
функций, графики которых изображены в верхнем ряду, найдите график
её производной.
У
у/
1
*
2
3
*
*
4
*
5
*

4.

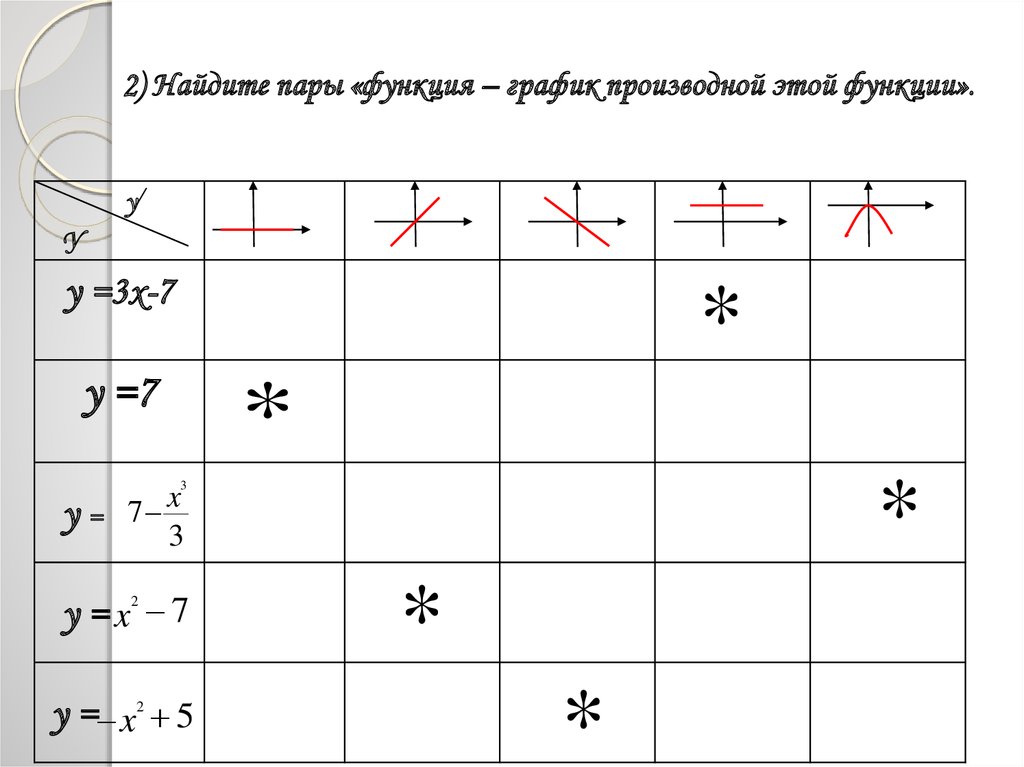
2) Найдите пары «функция – график производной этой функции».
у/
У
у =3x-7
*
у =7
*
*
3
у=
7 x
3
у =x 7
2
у = x 5
2
*
*

5.

3) Завершите фразы: «Если на отрезке [1; 3]
производная …, то на этом отрезке функция у…
то
Монотонно
возрастает
Если
Имеет
Имеет
Постоянна Монотонно
максимум
минимум
убывает
во
во
внутренней внутренней
точке
точке
*
у/=-5
у/=2-х
у/=1+2х
у/=0
у/=5
*
*
*
*

6.

Тема урока
«Применение
производной для
решения задач»

7. Решение задач

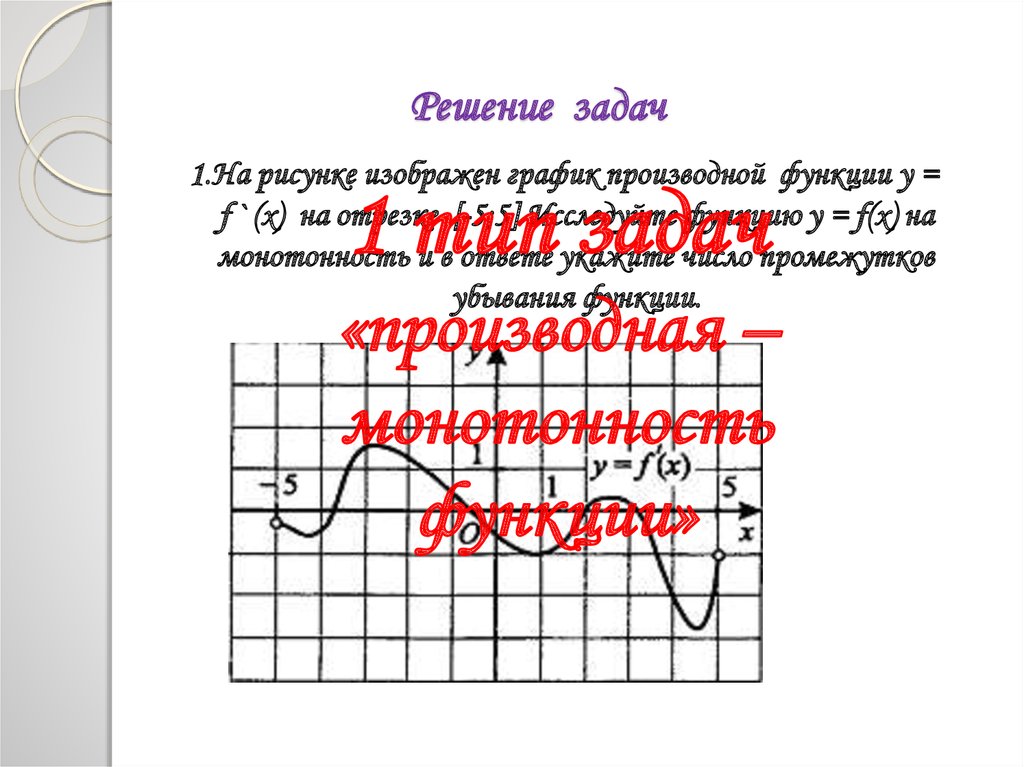
1.На рисунке изображен график производной функции у =
f ` (x) на отрезке [-5;5] Исследуйте функцию y = f(x) на
монотонность и в ответе укажите число промежутков
убывания функции.
1 тип задач
«производная –
монотонность
функции»

8.

f `(x)
-5
f(x)
-
+
-
+
5
Ответ: 3

9. 2.Функция у=f(x) определена на отрезке [-2;3]. На рисунке изображен график производной функции у =f `(x). В какой точке отрезка

функция принимает наименьшее значение?
f ` (x)
f(x)
-2
3
Ответ: 3

10. 3.На рисунке изображен график производной у = f ` (x). Исследуйте функцию y = f(x) на монотонность и в ответе укажите число

точек эктремума.
Ответ: 2

11.

4. На рисунке изображён график функции y=f(x) и отмечены шесть точек
на оси абсцисс: x1,x2,x3,…,x6. В скольких из этих точек производная
функции f(x) отрицательна, положительна ?
Ответ: 2; 4

12.

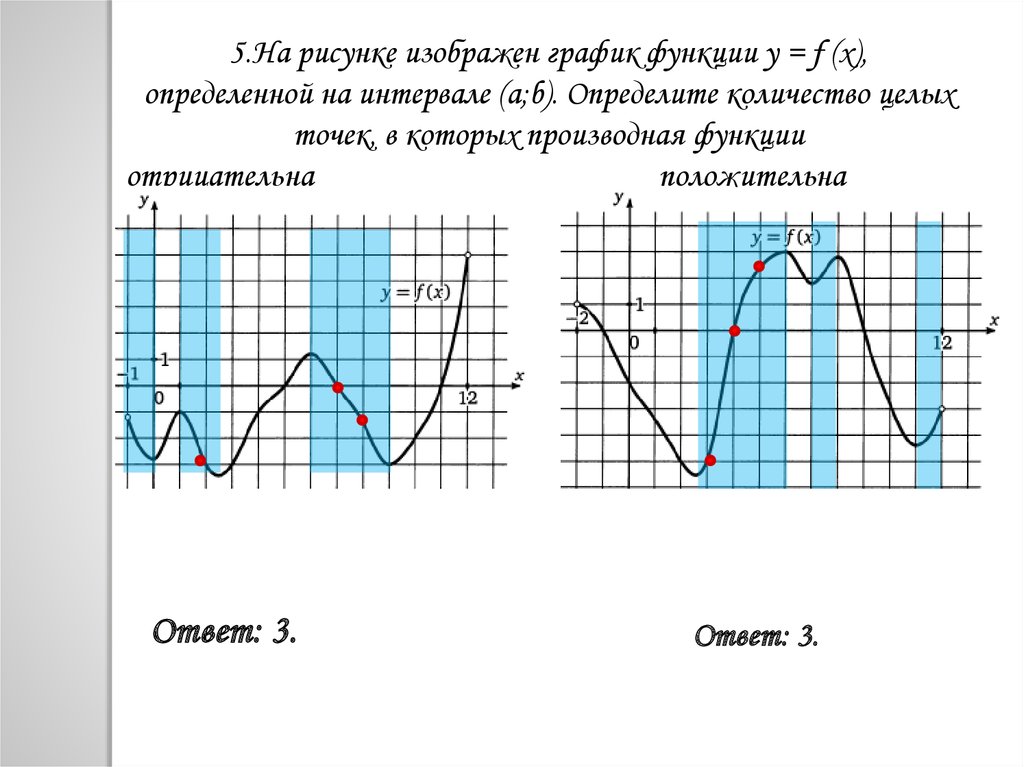
5.На рисунке изображен график функции y = f (x),
определенной на интервале (a;b). Определите количество целых
точек, в которых производная функции
отрицательна
положительна
Ответ: 3.
Ответ: 3.

13.

f `(x) > 0 y= f(x) – возрастает
f `(x) < 0 y= f(x) - убывает

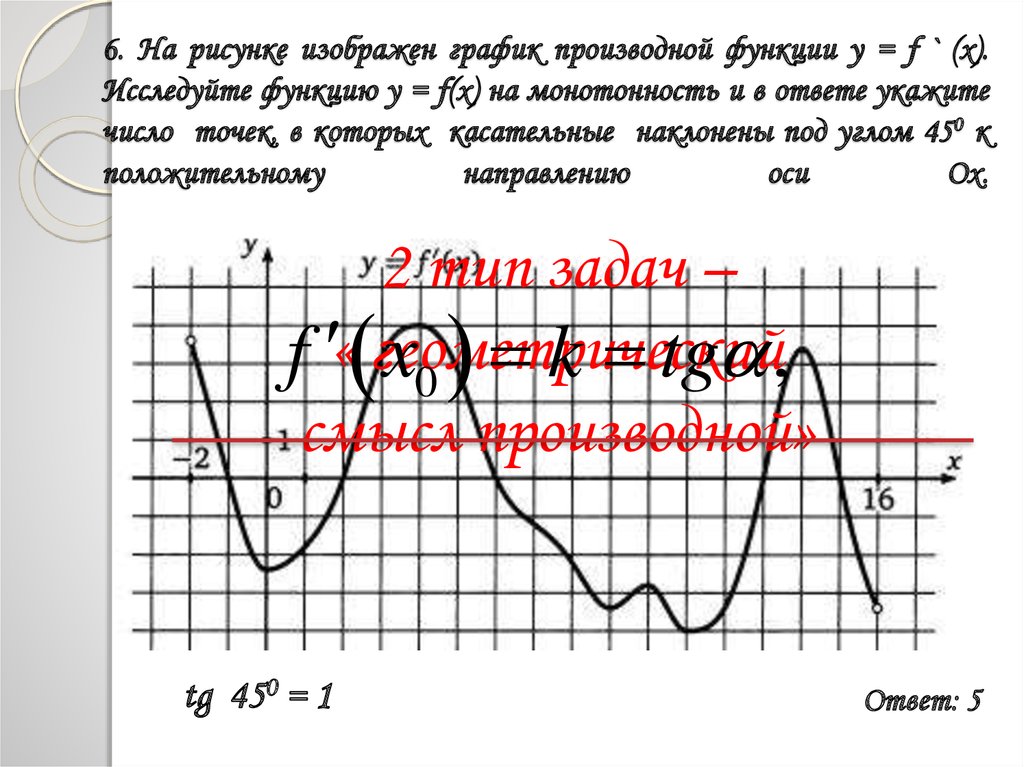
14. 6. На рисунке изображен график производной функции у = f ` (x). Исследуйте функцию y = f(x) на монотонность и в ответе укажите

число точек, в которых касательные наклонены под углом 450 к
положительному
направлению
оси
Ох.
2 тип задач –
f « геометрический
x0 k tg ,
смысл производной»
tg 450 = 1
Ответ: 5

15. 7. На рисунке изображен график производной функции у = f ` (x). Найдите количество точек, в которых касательные к графику

функции y =f(x) параллельны прямой
у= 2х – 3 или совпадают с ней.
Ответ: 5

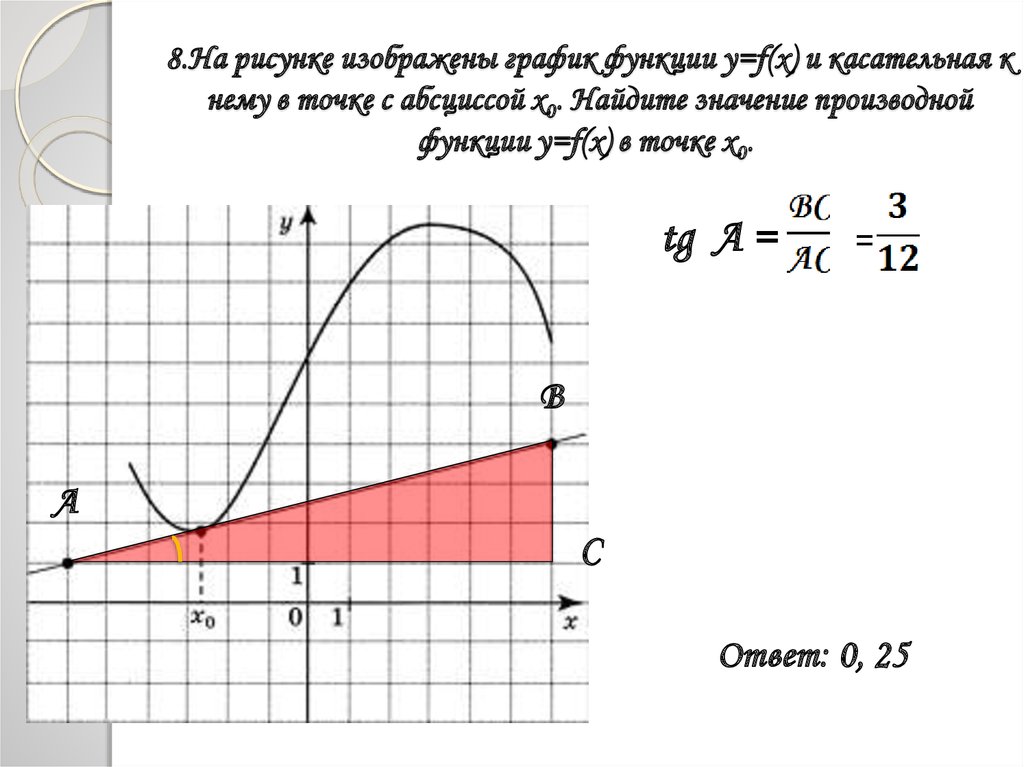
16. 8.На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции

y=f(x) в точке х0.
tg A =
=
В
А
С
Ответ: 0, 25

17. 9.На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции

y=f(x) в точке х0.
Ответ: 0,5

18.

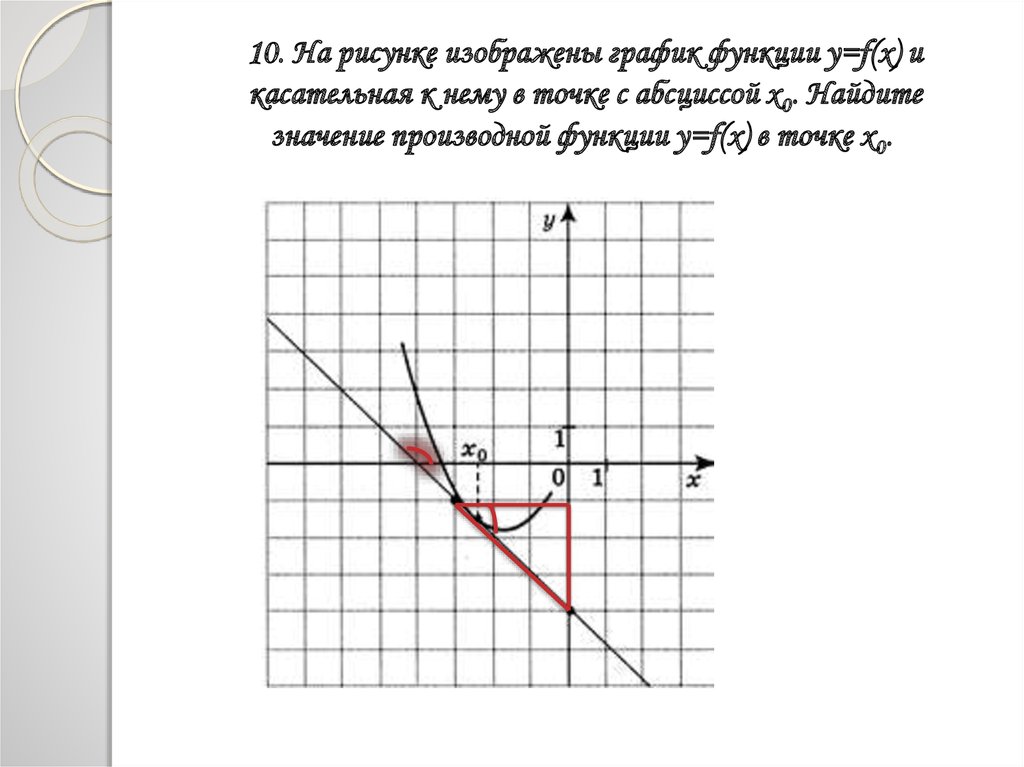
10. На рисунке изображены график функции y=f(x) и
касательная к нему в точке с абсциссой x0. Найдите
значение производной функции y=f(x) в точке х0.

19.

f `(x0) = tg α = k

20.

Решение задач.
11. Точка движется прямолинейно по закону
типскорость
задачв–момент времени t.
x(t) = 2t3 + t – 3. 3Найти
В какой момент
времени скорость будет равна 7
« физический
м/с (х – координата точки в метрах, t – время в
смысл
секундах).
производной»

21.

Самостоятельная работа
http://ege.yandex.ru/

22.

Домашнее задание:
По рисунку составить и записать 3 задачи
трех рассмотренных типов с их
решениями.