Похожие презентации:
Построение графиков квадратичных функции методом геометрических преобразований
1.
2.
•экспериментальным путем получить алгоритмы построенияграфиков функций видов y=ах2 ,у=а(х-т)2, у=ах2+n, у=а(х-т)2+n , если
известен график функции y=х2 ;
•научиться применять полученные алгоритмы к построению графиков
функций, заданных формулой у=ах2+вх + с .
•обобщить полученные знания для графика функции у=f(х).
•способствовать индивидуализации и дифференциации обучения с
помощью применения информационно-коммуникационных технологий
на уроках;
•развивать у учащихся логическое мышление, внимание; формировать
потребность в приобретении знаний
•воспитывать навыки самоконтроля, привычки к рефлексии;
•стимулировать ученика ,как активного исследователя.
3.
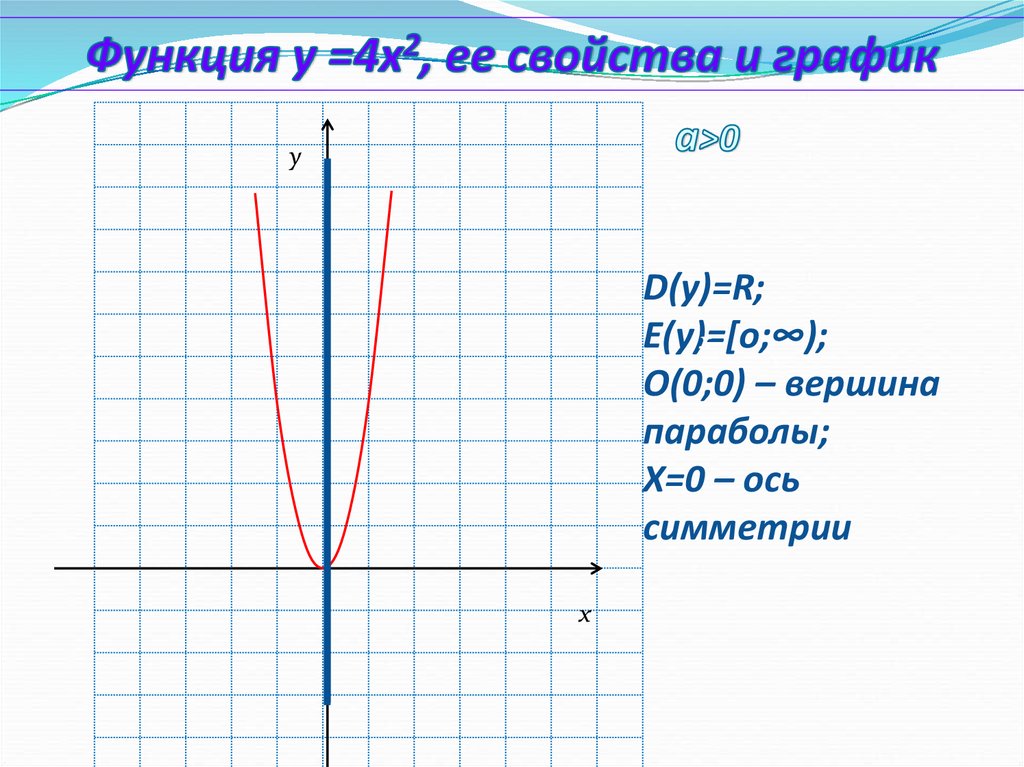
yD(у)=R;
E(у)=[о;∞);
О(0;0) – вершина
параболы;
Х=0 – ось симметрии
x
4.
yD(у)=R;
E(у)=[о;∞);
О(2;0) – вершина
параболы;
Х=2 – ось симметрии
x
5.
yу
D(у)=R;
E(у)=[о;∞);
х
О(0;0) – вершина
параболы;
Х=0 – ось
симметрии
О
x
6.
yу
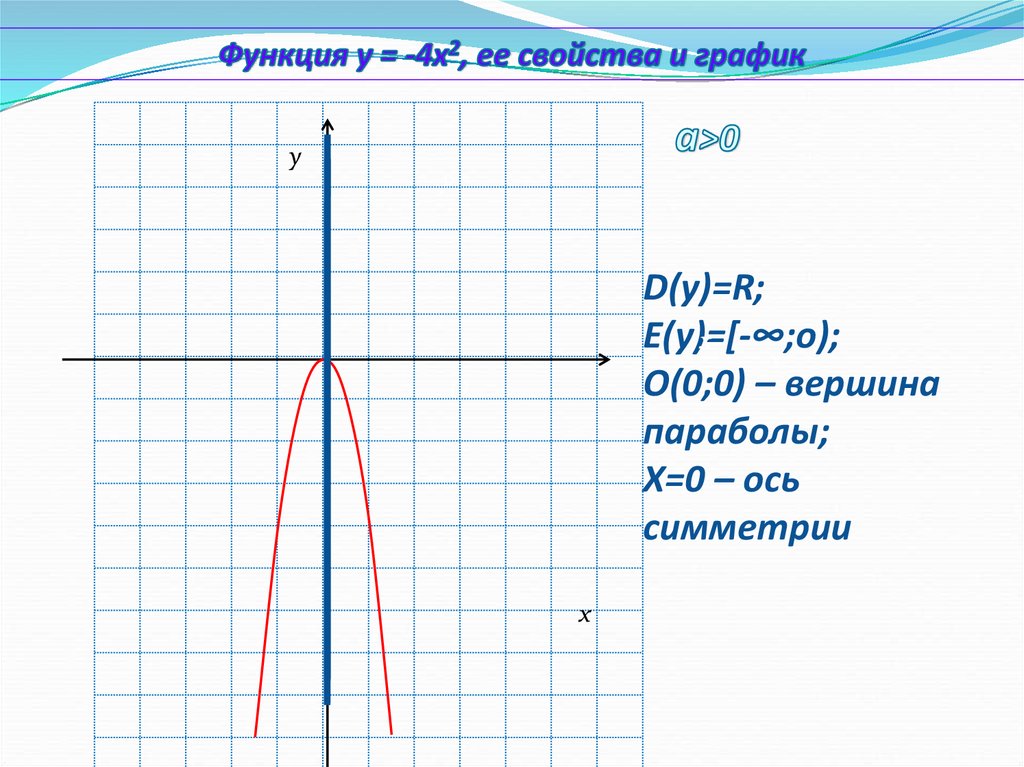
D(у)=R;
E(у)=[-∞;о);
х
О(0;0) – вершина
параболы;
Х=0 – ось
симметрии
О
x
7.
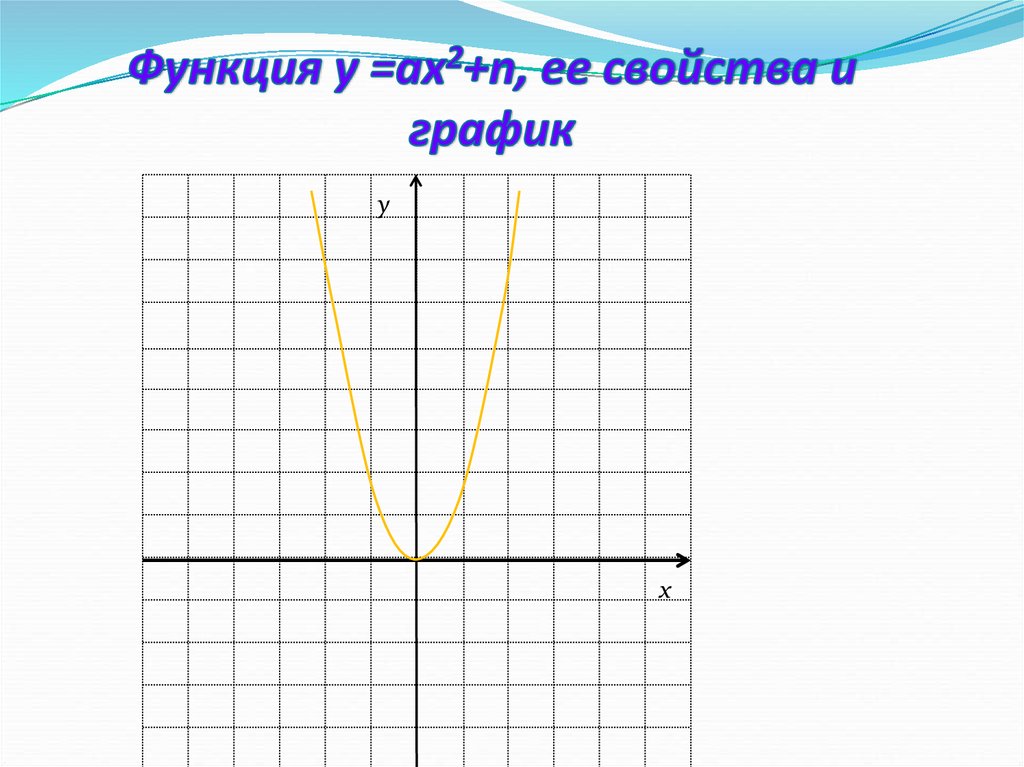
yD(у)=R;
E(у)=[2;∞);
О(0;0) – вершина
параболы;
Х=0 – ось симметрии
x
8.
yу
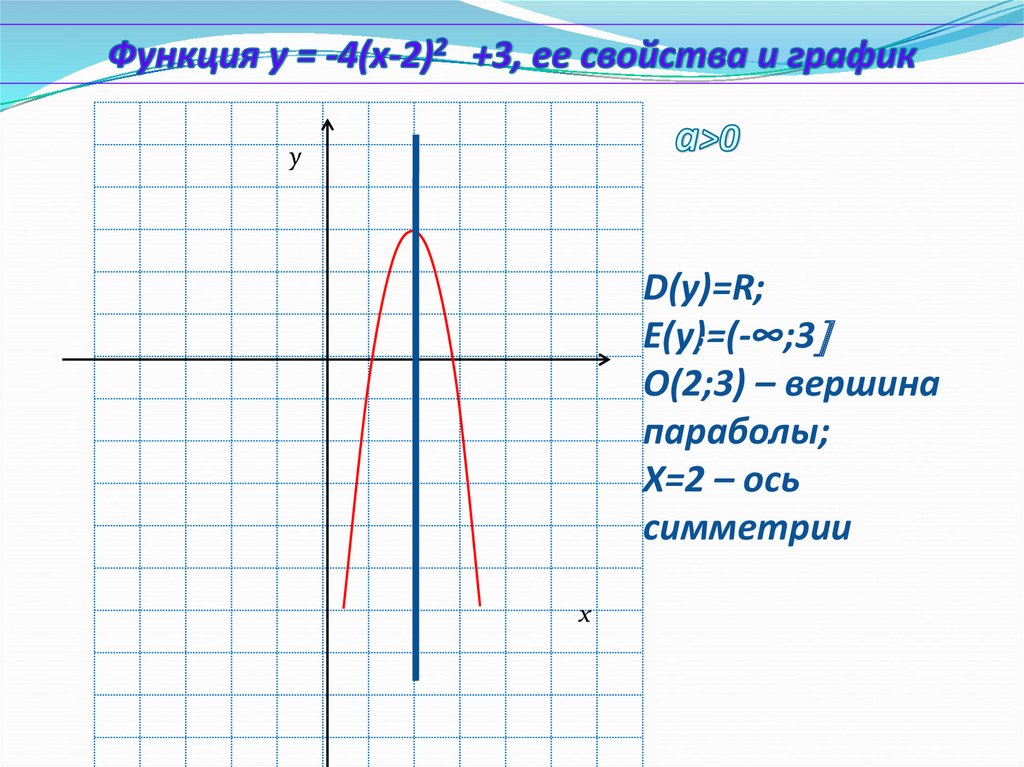
D(у)=R;
E(у)=(-∞;3
х
О(2;3) – вершина
параболы;
Х=2 – ось
симметрии
О
x
9.
yx
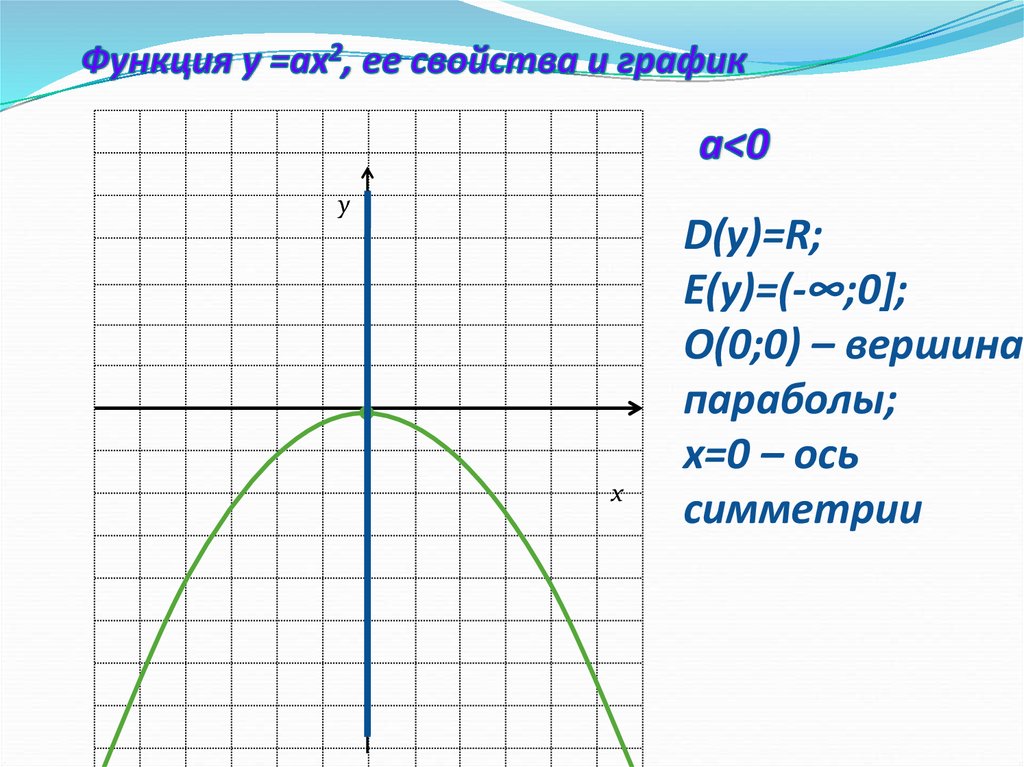
D(у)=R;
E(у)=(-∞;0];
О(0;0) – вершина
параболы;
х=0 – ось
симметрии
10.
Графиком функцииявляется парабола, которую
можно получить из графика
функции у =ах2 с помощью
параллельного переноса
вдоль оси у на n единиц вверх,
если n>0, или на –n единиц
вниз, если n<0
11.
yx
12.
yу
D(у)=R;
E(у)=[3;∞);
A(0;3) –
вершина
параболы;
х=0 – ось
симметрии
А
О
x
13.
Графиком функции у = а (х - т)2является парабола, которую
можно получить из графика
функции у = ах2 с помощью
параллельного переноса вдоль
оси х на т единиц вправо, если
т>0, или на –т единиц влево,
если т<0
14.
yx
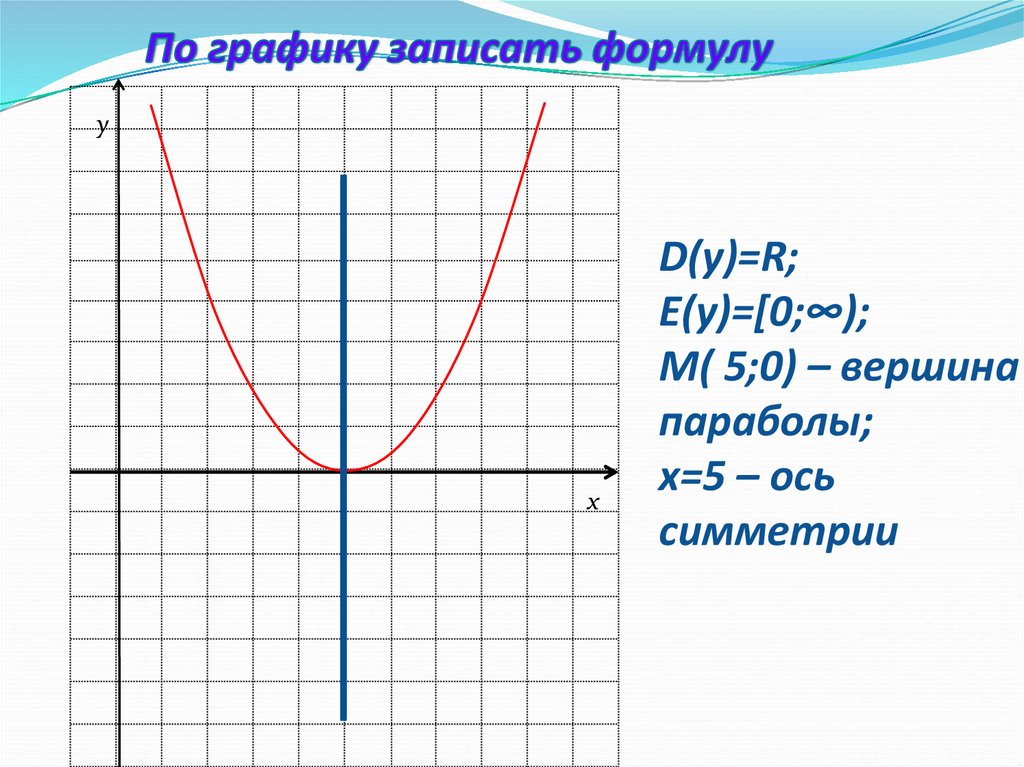
D(у)=R;
E(у)=[0;∞);
М( 5;0) – вершина
параболы;
х=5 – ось
симметрии
15.
yD(у)=R; E(у)=(-∞;0];
М(-5;0)- вершина
параболы;
Х=-5 – ось симметрии
x
16.
Графиком функции у = а (х - т)2 + nявляется парабола, которую можно
получить из графика функции у = ах2 с
помощью двух параллельных переносов:
сдвига вдоль оси х на т единиц вправо,
если т>0, или на – т единиц влево, если
т<0, и сдвига вдоль оси у на n единиц
вверх, если n >0, или на – n единиц вниз,
если n <0
17.
yx
D(у)=R;
E(у)=(-∞;4];
М(-2;4)- вершина
параболы;
х=-2 – ось
симметрии
18.
Квадратичной функцией называетсяфункция, которую можно задать
формулой вида
у =ах2 + вх + с,
где х - независимая переменная,
а, в, и с -некоторые числа,
причем а ≠ 0.
Графиком функции является парабола
19.
Графиком функции у=ах2+вх+сявляется парабола, которую
можно построить с помощью
«растяжений» и «сдвигов» ,
выделив полный квадрат.
20.
График функции g(х)= кf(х+m)+n можнополучить из графика функции f(x):
1) «растяжением» в к раз вдоль оси ОУ;
2) при к<0 – «зеркальным отображением»
(симметрией) относительно оси ОУ;
3) «сдвигом» (параллельным переносом) на
– m единиц вдоль оси ОХ;
4) «сдвигом» (параллельным
переносом) на n единиц вдоль оси
ОУ;
21.
•проводится анализ работ учащихся;•организуется самооценка учениками
своей деятельности;
•фиксируется степень соответствия
поставленной цели и результатов
деятельности;
•намечаются цели последующей
деятельности;
•комментируется домашнее задание.















 Математика
Математика








