Решение тригонометрических неравенств методом интервалов

1. Решение тригонометрических неравенств методом интервалов

Райкова Лидия Викторовна,
учитель математики МОУ «СОШ №8»

2. Проверка домашнего задания

x x 1 x 1 0
4 x x 5 0
-4
0
; 4 1;
-5
x 3
x 1 x 2
1
x
4
-3
x
; 5 3;4
2
x 1
4t 0
2
0
-2
-1
2 1;1
- 1/2
1 1
;
2 2
1/2
1
x
t

3. Устная работа

f x sin x x
2
2
cos x
f x
sin x
f x cos x cos x 1
sin x 1
f x
cos x
cos 2 x
f x
x 3

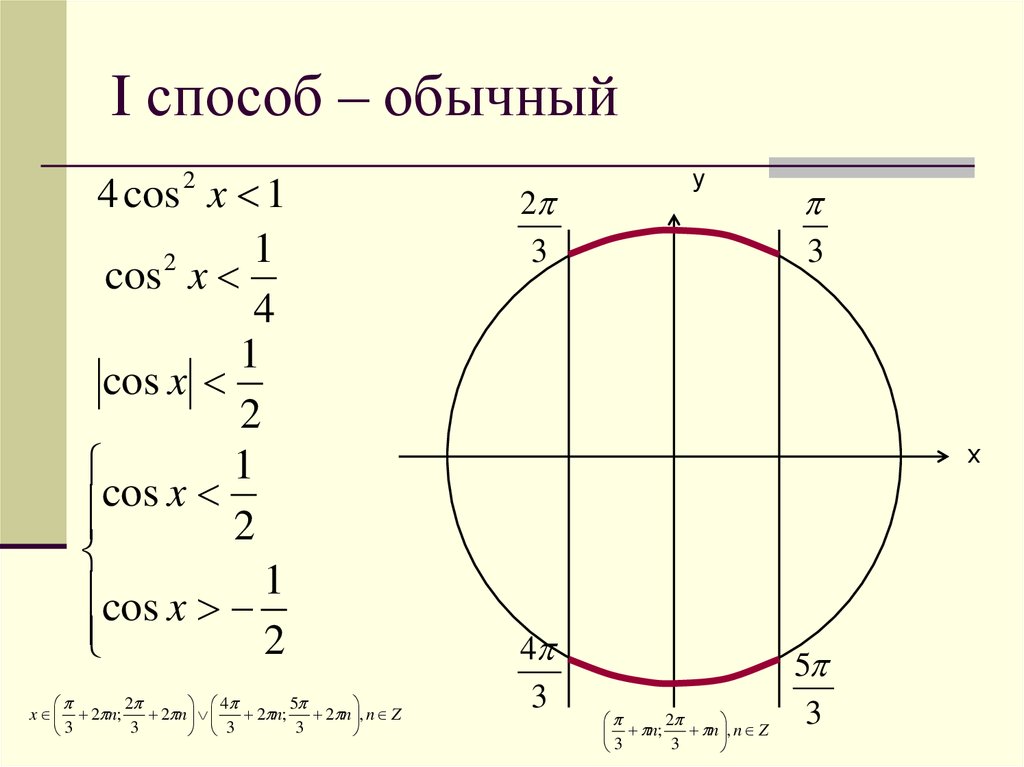
4. I способ – обычный

4 cos 2 x 1
1
2
cos x
4
1
cos x
2
1
cos x 2
cos x 1
2
2
5
4
x 2 n;
2 n
2 n;
2 n , n Z
3
3
3
3
2
3
y
3
х
4
3
2
n , n Z
n;
3
3
5
3

5. II способ – метод интервалов

4 cos x 1 0
1. Пусть f x 2 cos x 1 2 cos x 1
2
3.
2 cos x 1 0
2 cos x 1 0
4.
cos x 1 / 2
cos x 1 / 2
3
или
2
3
+
0
3
;x
2
4
5
;x
;x
;
3
3
3
+
+
0
x
D f ;
2.
+
4
3
5
3
+
3
2
3
2
5
4
x 2 n;
2 n
2 n;
2 n , n Z
3
3
3
3
+
4
3
5
3
2
Х
2
Х
2
n
;
n , n Z
3
3

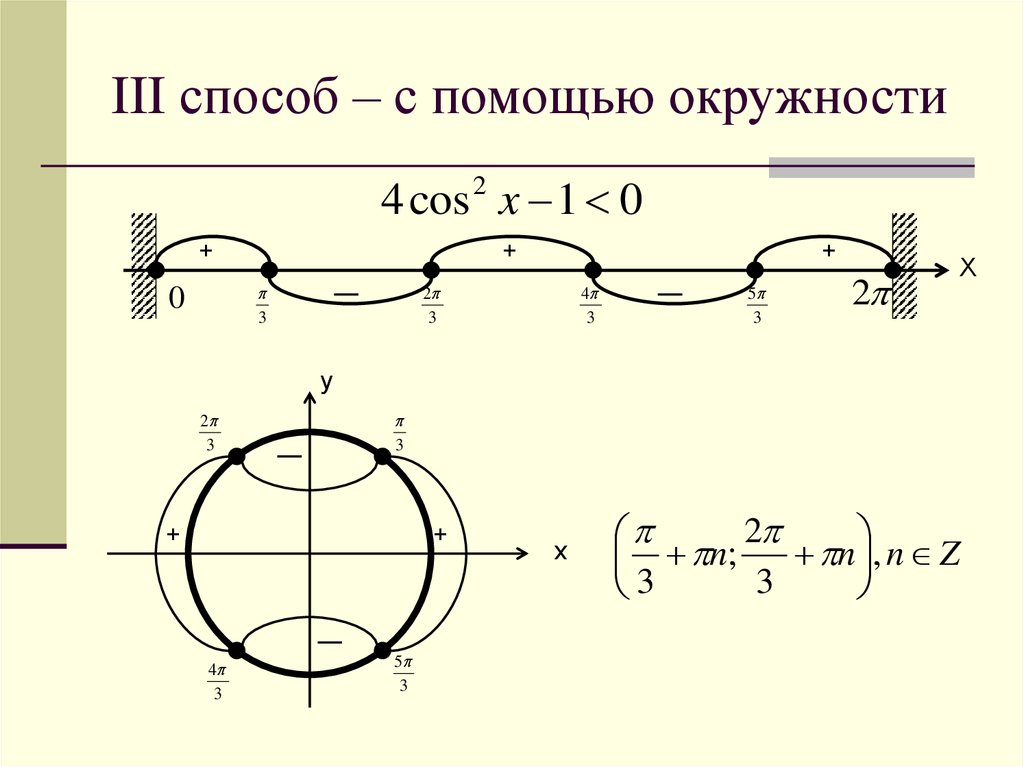
6. III способ – с помощью окружности

4 cos 2 x 1 0
+
+
3
0
+
2
3
4
3
5
3
2
у
2
3
3
+
+
4
3
5
3
х
2
n , n Z
n;
3
3
Х

7. Пример 1.

sin 3 x sin x
0
cos x sin 2 x
Пример 1.
1.
f x
sin 3x sin x
cos x sin 2 x
cos x 0
2. D f :
sin 2 x 0
x 2
x 0
x 3 2
x 2
у
x 2 n
x n 2 , n Z
x 3 2
x
3
2
3
+
+
х
0
3. Нули функции:
sin x 0 x n
sin 3x 0 x n 3 , n Z
x 0
x 0
x
x 3 ; x 2 3 ; x ; x 4 3 ; x 5 3
4
3
+
+
5
3

8. Домашнее задание

2 sin x 1
2
(двумя способами)
2 sin x 3
sin x
2 cos x 2 0
sin x sin 3 x
0
cos x sin 2 x

9. Благодарю за внимание!