Похожие презентации:
Решение тригонометрических уравнений с отбором корней на заданном промежутке
1.
2.
3. 23.03.2012
Решениетригонометрических уравнений
с отбором корней
на заданном промежутке
4.
Решение тригонометрических уравнений сотбором корней на заданном промежутке
Тригонометрические
формулы
Методы решения
тригонометрических
уравнений
Формулы корней
простейших
тригонометрических
уравнений
Способы отбора
корней
5. Тригонометрические формулы
arccos(-0,5)sin( 0,5π+x)
arcsin(-0,5)
sin 6x
cos²x-1
cos (1,5π-x)
сos(-4π/3) Tg²(1,5π+x)
3sin²4x+3cos²4x
вперед
2tg405°
sin 150°
cos²x-sin²x
6. Методы решений тригонометрических уравнений
Основные методы:• замена переменной,
• разложение на множители,
•однородные уравнения,
прикладные методы:
• по формулам преобразования суммы в произведение
и произведения в сумму,
• по формулам понижения степени,
• универсальная тригонометрическая подстановка
• введение вспомогательного угла,
• умножение на некоторую тригонометрическую функцию.
7. Формулы корней простейших тригонометрических уравнений
Формулы корней тригонометрическихSin x =a,
X = (-1)n arcsin a +Пn
n Z
Частные
Cos x = a,
X= ± arccos a + 2Пn
n Z
случаи решения
sin x = 0
X = Пn, n Z
cos x = 0
X = П/2 + Пn, n Z
sin x = 1,
X = П/2 + 2 Пn, n Z
cos x = 1,
X = 2Пn, n Z
sin x = -1,
X = -П/2 + 2Пn, n Z
cos x = -1,
X = П + 2 Пn, n Z
уравнений
tg x = a,
x = arctg a + Пn
n Z
уравнений
tg x = 0
X = Пn, n Z
8. Способы отбора корней тригонометрических уравнений на заданном промежутке
• Арифметический способПеребор значений целочисленного параметра n и
вычисление корней
• Алгебраический способ
Перебор значений целочисленного параметра n и
вычисление корней
• Геометрический способ
Изображение корней на тригонометрической
окружности с последующим отбором с учетом
имеющихся ограничений
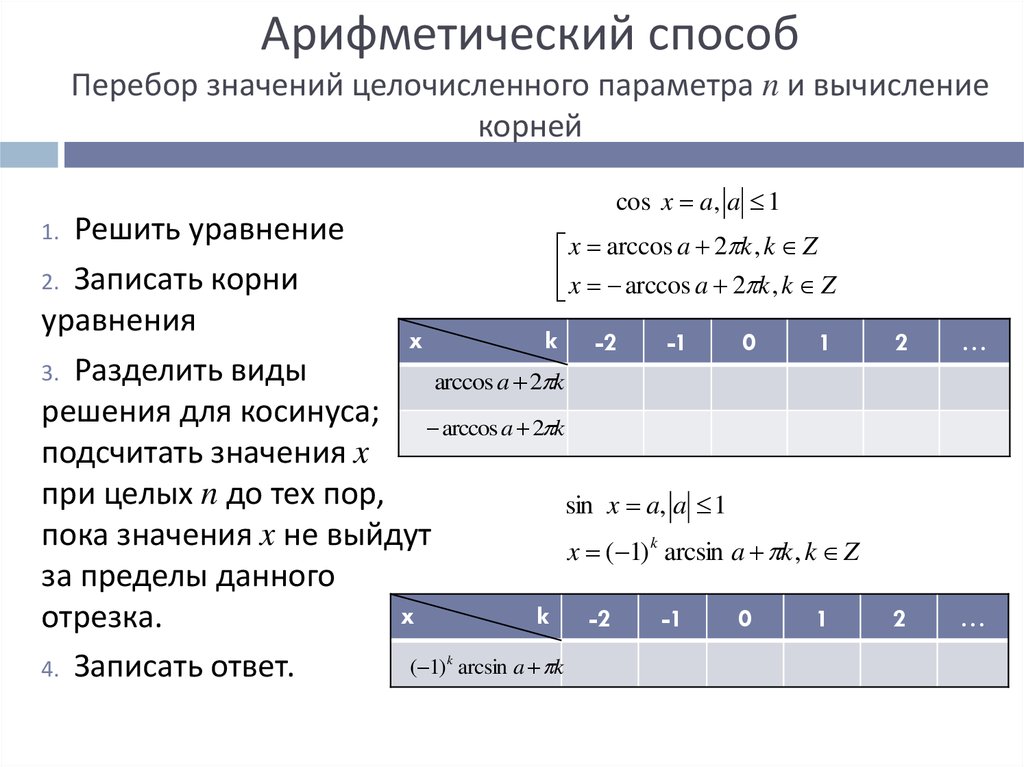
9. Арифметический способ Перебор значений целочисленного параметра n и вычисление корней
cos x a, a 1Решить уравнение
x arccos a 2 k , k Z
x arccos a 2 k , k Z
2. Записать корни
уравнения
x
k -2
-1
0
1
3. Разделить виды
arccos a 2 k
решения для косинуса; arccos a 2 k
подсчитать значения x
при целых n до тех пор,
sin x a, a 1
пока значения x не выйдут
x ( 1) k arcsin a k , k Z
за пределы данного
x
k
-2
-1
0
1
отрезка.
( 1) arcsin a k
4. Записать ответ.
1.
k
2
…
2
…
10. Алгебраический способ Решение неравенства относительно неизвестного параметра n и вычисление корней
Записать двойное неравенстводля неизвестного (x),
соответственное данному
отрезку или условию; решить
уравнение.
1.
Для синуса и косинуса разбить
решения на два.
2.
Подставить в неравенство
вместо неизвестного (x)
найденные решения и решить
его относительно n.
3.
Учитывая, что n принадлежит
Z, найти соответствующие
неравенству значения n.
4.
Подставить полученные
значения n в формулу корней.
5.
cos x a, a 1, c; d
x arccos a 2 k , k Z
x arccos a 2 k , k Z
с arccos a 2 k d
с arccos a 2 k d
Т.к. k Z , то k1 ...; x1 ...
k2 ...; x2 ...
sin x a, a 1, c; d
x arcsin a 2 k , k Z
x arcsin a 2 k , k Z
с arcsin a 2 k d
с arcsin a 2 k d
Т.к. k Z ,
то k1 ...; x1 ...
k2 ...; x2 ...
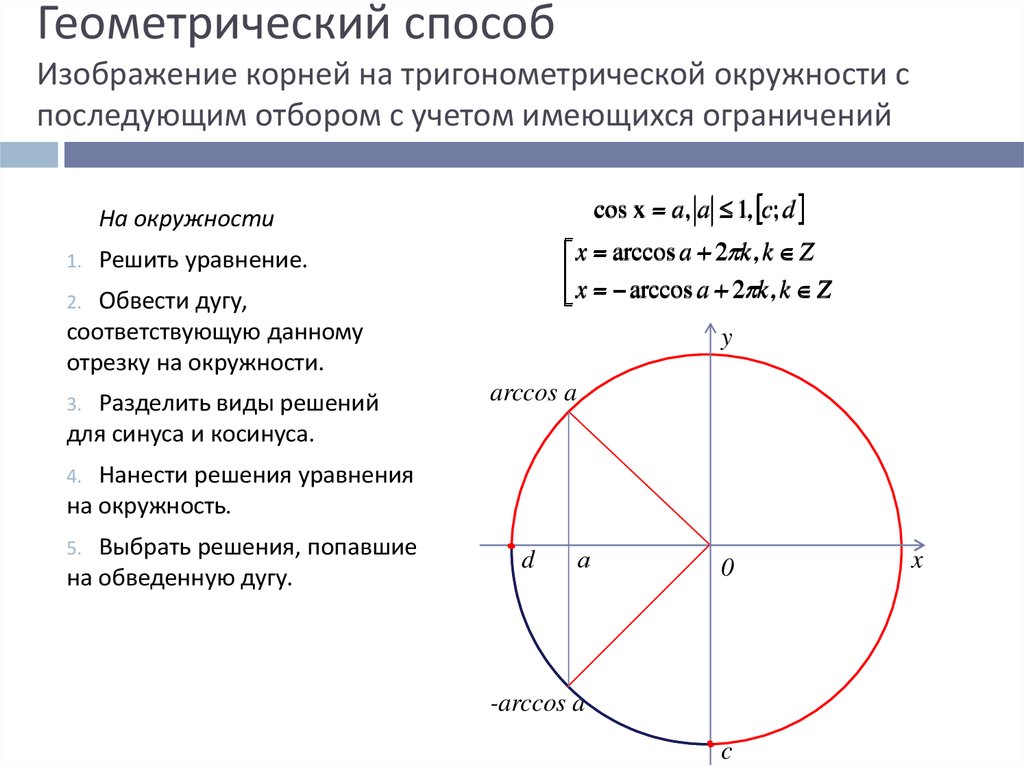
11. Геометрический способ Изображение корней на тригонометрической окружности с последующим отбором с учетом имеющихся ограничений
cos x a, a 1, c; dНа окружности
1.
x arccos a 2 k , k Z
x arccos a 2 k , k Z
Решить уравнение.
Обвести дугу,
соответствующую данному
отрезку на окружности.
2.
Разделить виды решений
для синуса и косинуса.
3.
y
arccos a
Нанести решения уравнения
на окружность.
4.
Выбрать решения, попавшие
на обведенную дугу.
5.
d
а
0
-arccos a
c
x
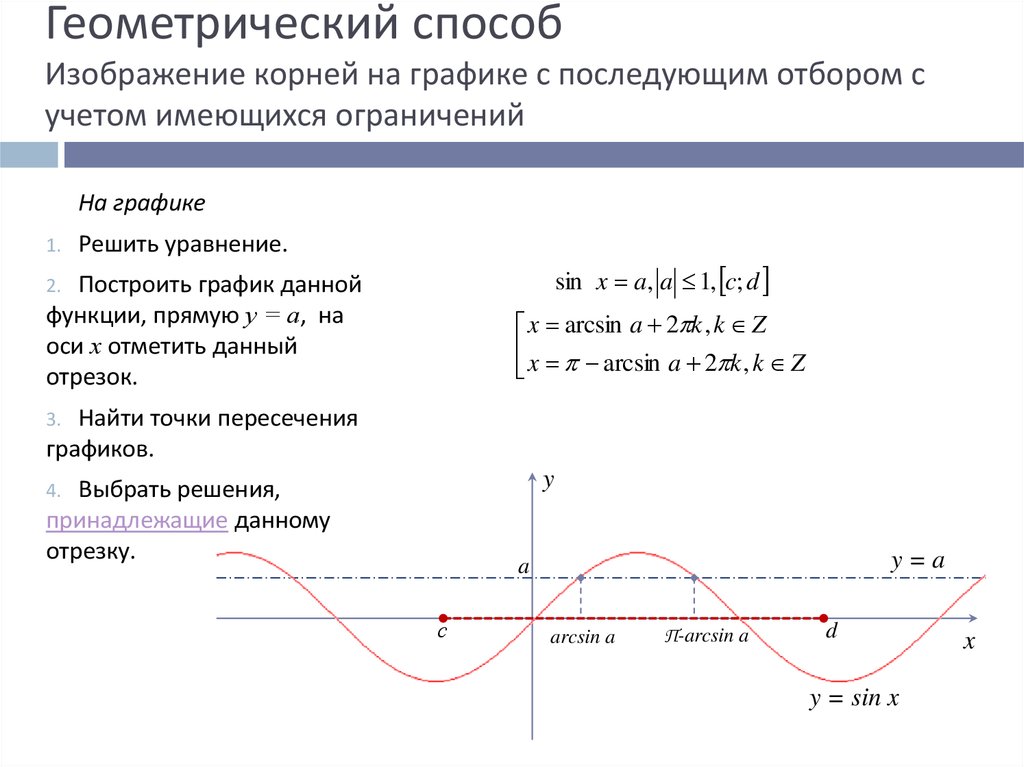
12. Геометрический способ Изображение корней на графике с последующим отбором с учетом имеющихся ограничений
На графике1.
Решить уравнение.
sin x a, a 1, c; d
Построить график данной
функции, прямую у = а, на
оси х отметить данный
отрезок.
2.
x arcsin a 2 k , k Z
x arcsin a 2 k , k Z
Найти точки пересечения
графиков.
3.
y
Выбрать решения,
принадлежащие данному
отрезку.
4.
y=a
a
с
arcsin a
П-arcsin a
d
y = sin x
x
13.
Ответы14.
Пример 3. Найти все корни уравнения10 cos 2 (
2
которые удовлетворяют условию x [
Решение.
10sin2 x = – cos 2x + 3;
10sin2 x = 2sin2 x – 1 + 3,
8sin2 x = 2;
1
sin 2 x ;
4
1
sin x ;
2
k
x
(
1
)
k , k Z ,
6
x ( 1) m ( ) m, m Z ;
6
x
6
n, n Z ;
7
2 x) 3,
2
2 19
;
].
3 12
y
2
5
6
6
0
7
6
С помощью числовой окружности получим:
x) sin(
x
3
2
6
15.
Выберем корни, удовлетворяющие условию задачи.Из первой серии: 2 n 19 , n Z ;
3
6
12
8 2 12 n 19 , n Z ;
10 12n 17, n Z .
Следовательно n=0 или n=1, то есть x ,
6
x 7 .
6
2
19
n
,n Z;
3
6
12
8 2 12 n 19 , n Z ;
Из второй серии:
6 12n 21, n Z .
Следовательно n=0 или n=1, то есть
x
,
6
x 5 .
6
Ответ : {
5 7
;
6 6
;
6
}.
16.
Самый лучший способдля достижения правильного
и быстрого результата
это тот, который лучше всего усвоен
конкретным учеником.












 Математика
Математика








