"Чтение" графика функции

1.

Авт. Г.Н.Зинченко

2.

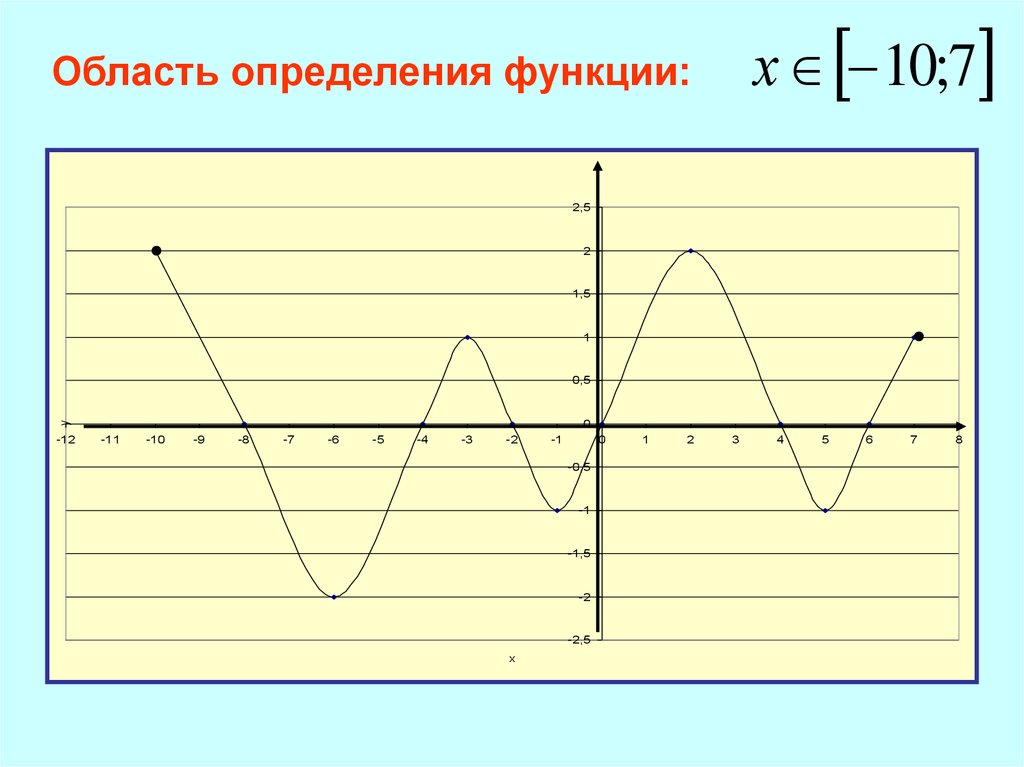
х 10;7
Область определения функции:
2,5
2
1,5
1
0,5
0
у
-12
-11
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
-0,5
-1
-1,5
-2
-2,5
х
1
2
3
4
5
6
7
8

3.

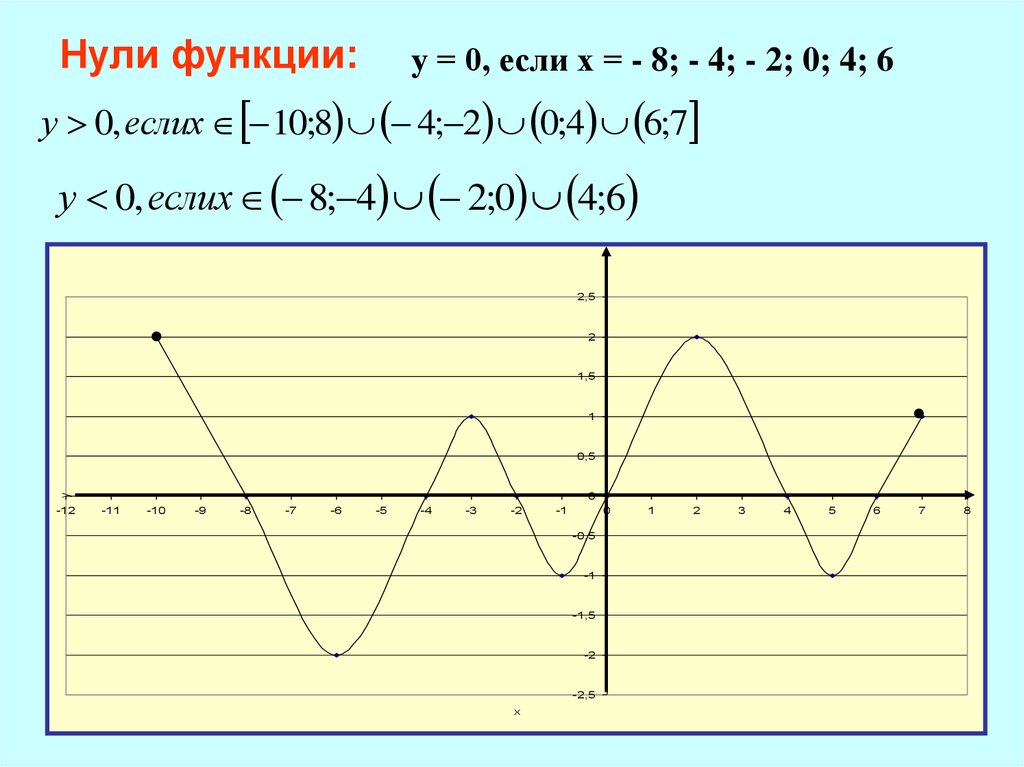
Нули функции:
у = 0, если х = - 8; - 4; - 2; 0; 4; 6
у 0, еслих 10;8 4; 2 0;4 6;7
у 0, еслих 8; 4 2;0 4;6
2,5
2
1,5
1
0,5
0
у
-12
-11
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
-0,5
-1
-1,5
-2
-2,5
х
1
2
3
4
5
6
7
8

4.

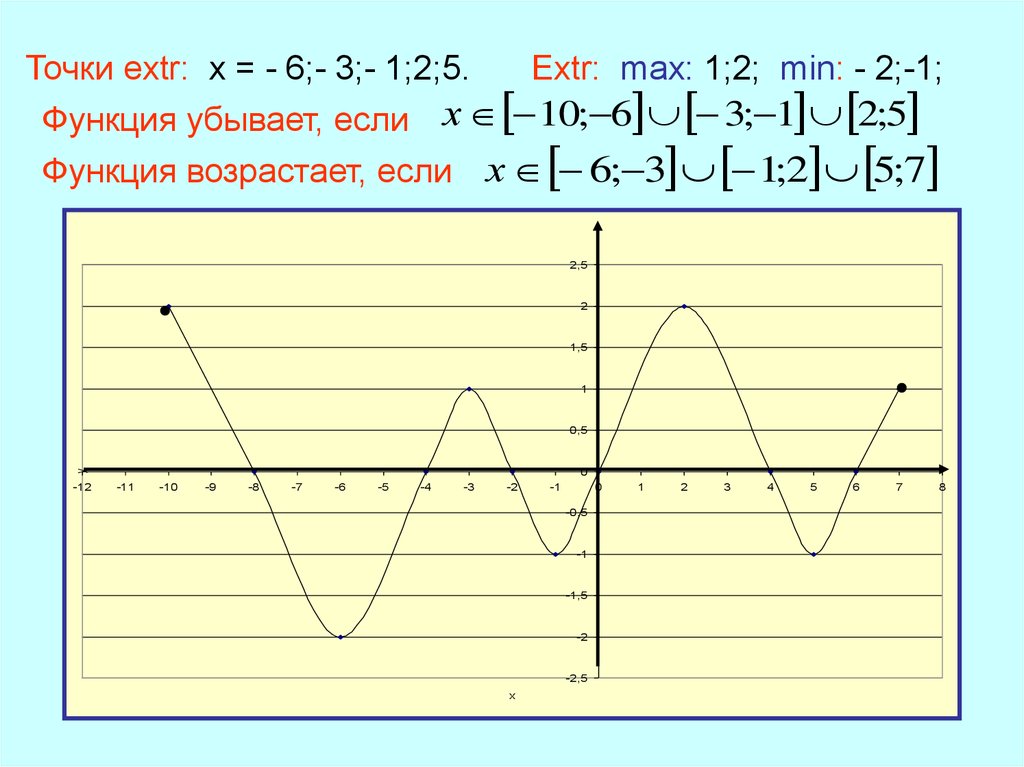
Точки extr: x = - 6;- 3;- 1;2;5.
Extr: max: 1;2; min: - 2;-1;
Функция убывает, если х 10; 6 3; 1 2;5
Функция возрастает, если х 6; 3 1;2 5;7
2,5
2
1,5
1
0,5
0
у
-12
-11
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
-0,5
-1
-1,5
-2
-2,5
х
1
2
3
4
5
6
7
8

5.

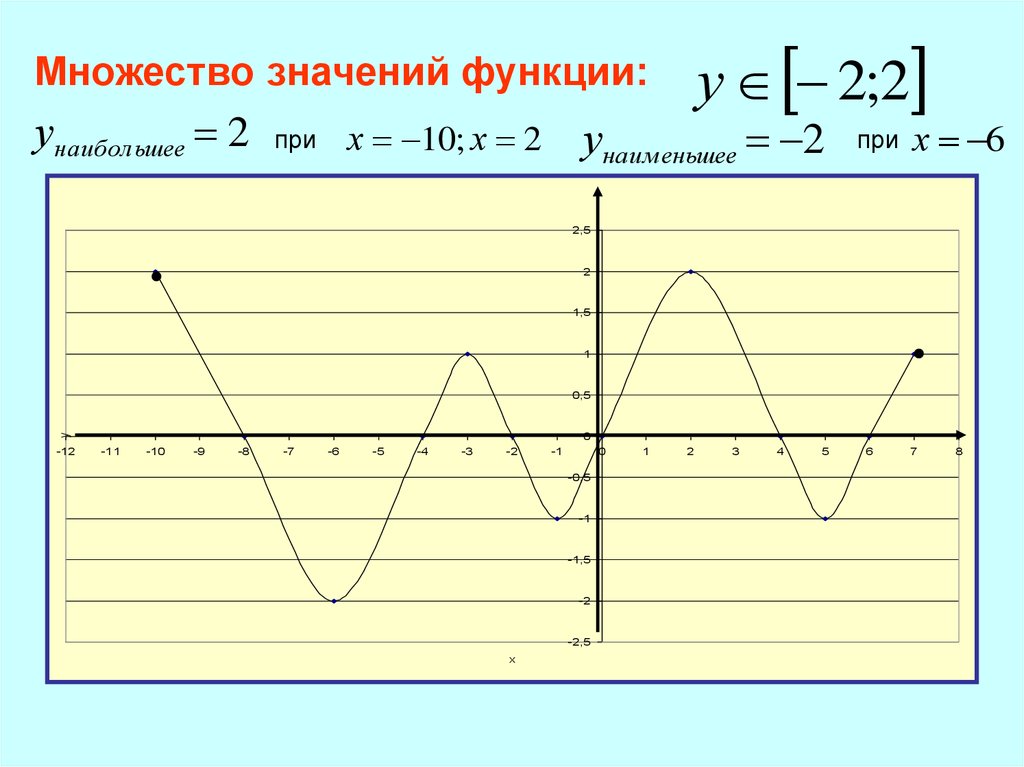
у 2;2
Множество значений функции:
унаибольшее 2
унаименьшее 2
х 10; х 2
при
при
х 6
2,5
2
1,5
1
0,5
0
у
-12
-11
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
-0,5
-1
-1,5
-2
-2,5
х
1
2
3
4
5
6
7
8

6.

*Какие еще свойства могут иметь функции?
*Какие функции называются четными
(нечетными)?
*Почему графики четных (нечетных)
функций узнаваемы?
*Какие функции называются
периодическими?
*Почему графики периодических функций
узнаваемы?