Решение логических задач на уроках математики

1.

Предмет математики настолько серьезен,
что нельзя упускать случая сделать его
немного занимательным.
Блез Паскаль
1

2.

Технология развития критического мышления
технология организации учебного и
воспитательного процесса,
которая применима к любой программе
и любому предмету.
2

3.

3

4.

Задачи
• Создание условий для профессионального общения;
• Повышение профессионального мастерства и
квалификации участников;
• Распространение опыта работы по применению
технологии развития критического мышления
4

5.

Логика- наука о законах и формах мышления
Логическое мышление- мыслительный процесс, при
котором человек использует логические понятия и конструкции,
которому свойственна доказательность, рассудительность, и с целью
которого является получение обоснованного вывода из имеющихся
предпосылок
Задачи на логику – это такие задачи, при решении которых
определяющим фактором является обнаружение связей между данными
задачи и их анализ, при чем, результатом является составление
последовательных суждений, а любые вычисления и построения играют
вспомогательную роль или отсутствуют.
Толковый словарь Георгий Данилович Ожегов
5

6. Познавательная деятельность учащихся

Уровень устойчивого интереса
(автор Г. Н. Казанцева)
90%
Уровень познавательной
активности(автор Б. К. Пашнев )
Данный предмет интересен
80%
50%
Нравится, как преподает
учитель
70%
60%
50%
48%
45%
38%
40%
Предмет нужно знать всем
Высокий
уровень
35%
50%
40%
30%
Предмет нужен для
будущей профессии
30%
Предмет занимательный
20%
25%
Средний
уровень
25%25%
14%
15%
Хорошие взаимоотношения
с учителем
20%
10%
10%
5%
Учитель интересно
объясняет
0%
5 класс
Низкий
уровень
0%
5 класс
6 класс
6класс
Познавательная потребность
(автор В. С. Юркевич)
45%
43%
40%
35%
30%
25%
40%41%
Выражена
сильно
32%
25%
18%
20%
Выражена
умеренно
15%
Выражена
слабо
10%
5%
0%
5 класс
6 класс
6

7.

Говорят уравнение
вызывает сомнение,
но итогом сомнения
может быть озарение!
7

8. Путешествие в математику

28k + 30n + 31m = 365
Путешествие в математику
План путешествия:
1. Развиваем гибкость ума через решение задач.
2. Ситуации в жизни такие: либо сложные, либо
простые.
3. Без логики нет математики.
4. В технологию тропинки одолеем без запинки.
5. Точка соприкосновения.
6. И фокусы покажем, и секрет расскажем.
8

9.

28k + 30n + 31m = 365
I этап. Развиваем гибкость ума
через решение задач.
У двух зрячих один брат слепой,
но у слепого нет
зрячих братьев. Как это
может быть?
9

10. II этап. Ситуации в жизни такие: либо сложные, либо простые

28k + 30n + 31m = 365
II этап. Ситуации в жизни такие: либо
сложные, либо простые
Трём приятелям вручили
четыре яблока. Как, не
разрезая и не
выбрасывая яблок,
разделить их между
приятелями так,
чтобы каждый получил
не больше остальных?
Назовите два числа, у
которых количество
цифр равно
количеству букв,
составляющих
название каждого из
этих чисел.
10

11. IIIэтап. Без логики нет математики

28k + 30n + 31m = 365
IIIэтап. Без логики нет математики
Идут рядом два человека,
один из них – отец
сына другого.
Как такое может быть?
11

12. IV этап. В технологию тропинки одолеем без запинки.

28k + 30n + 31m = 365
IV этап. В технологию тропинки одолеем без
запинки.
В кафе предлагают два первых блюда: борщ,
рассольник и четыре вторых блюда: гуляш,
котлеты, сосиски, пельмени. Укажите все
обеды из первого и второго блюд, которые
может заказать посетитель.
12

13. V этап. Точка соприкосновения:

28k + 30n + 31m = 365
V этап. Точка соприкосновения:
Человек прыгает со стула.
В руках он держит весы,
на чашке которых лежит
груз 10 кг. На каком
делении будет стоять
стрелка весов во время
падения?
13

14. VI этап. И фокусы покажем, и секрет расскажем!

28k + 30n + 31m = 365
VI этап. И фокусы покажем, и секрет
расскажем!
Вопрос:
без чего невозможно
сделать табуретку,
даже если есть
все-все инструменты
и все-все деревяшки,
гвозди, клей?
14

15. Оригами

28k + 30n + 31m = 365
Оригами
Давно в древние века, когда люди в Японии
приходили в храм, то в качестве подношений
приносили фигурки, сложенные из бумаги оригами. Недаром «ори» означает складывать, а
«ками» -«бумага».
Среди любителей оригами можно
отметить Леонардо да Винчи
Л.Н.Толстой
15

16. Правильные многогранники

28k + 30n + 31m = 365
Правильные многогранники
Тетраэдр
Гексаэдр
Октаэдр
Додекаэдр
Икосаэдр
16

17. Другие многогранники

28k + 30n + 31m = 365
Другие многогранники
Кубооктаэдр
Усечённый
октаэдр
Открытый
ромбоикосододекаэдр
Открытый усечённый
икосододекаэдр
Ромбокубооктаэдр
17

18. Классические фигуры

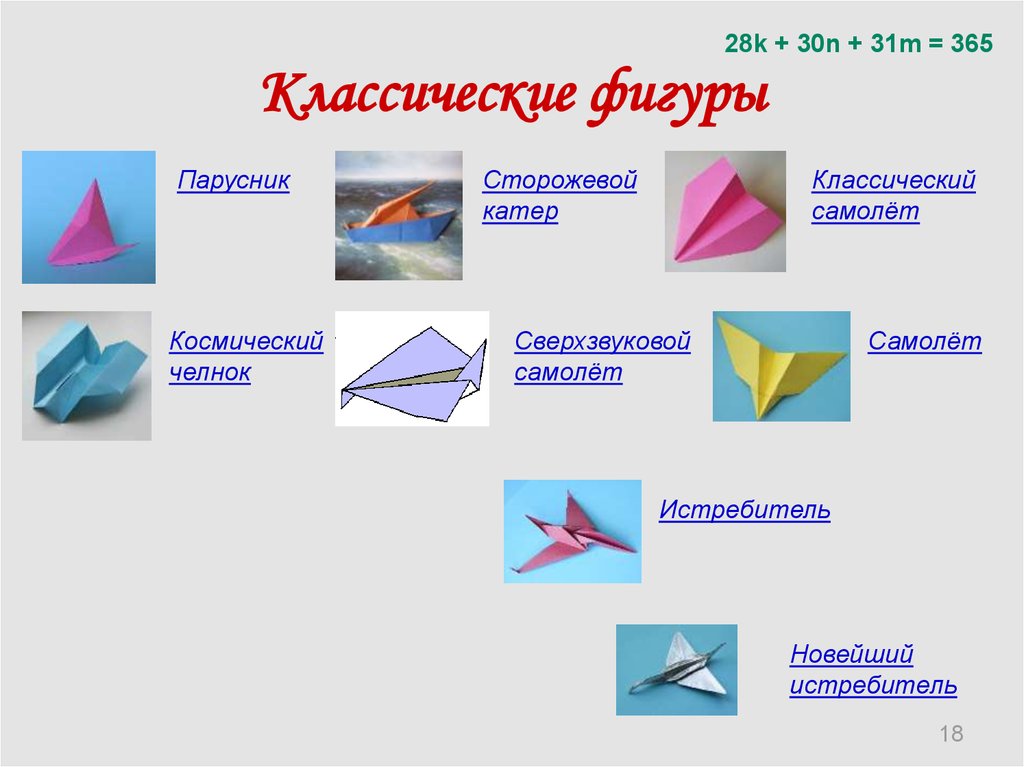
28k + 30n + 31m = 365
Классические фигуры
Парусник
Космический
челнок
Сторожевой
катер
Классический
самолёт
Сверхзвуковой
самолёт
Самолёт
Истребитель
Новейший
истребитель
18

19. Классические фигуры

28k + 30n + 31m = 365
Классические фигуры
Боевой катер
Стелс
Ракета
Яхта
Ракета
Лодка с
вёслами
Катамаран
19

20. Оригами

28k + 30n + 31m = 365
Оригами
20

21. “Смотреть – не значит видеть!”

28k + 30n + 31m = 365
“Смотреть – не значит видеть!”
k= 1
n= 4
m= 7
21

22.

28k + 30n + 31m = 365
Все правильные многогранники были известны еще в Древней Греции.
Великий древнегреческий мыслитель Платон считал, что мир строится из
четырёх «стихий» - огня, земли, воздуха и воды.
икосаэдр – как
самый обтекаемый
- воду;
куб – самая
устойчивая из
фигур – землю,
Тетраэдр
олицетворял огонь,
поскольку его вершина
устремлена вверх, как
у разгоревшегося
пламени;
октаэдр – воздух.
Пятый многогранник –
додекаэдр
символизировал весь
мир и почитался
главнейшим.
22

23.

1.Я не знал(а), что….
2.Мастер-класс научил меня…
3.Теперь я буду…..
23

24.

Журавлева Наталья Владимировна
приглашаю к сотрудничеству
[email protected]
24