Параметры зубошевинговальных станков

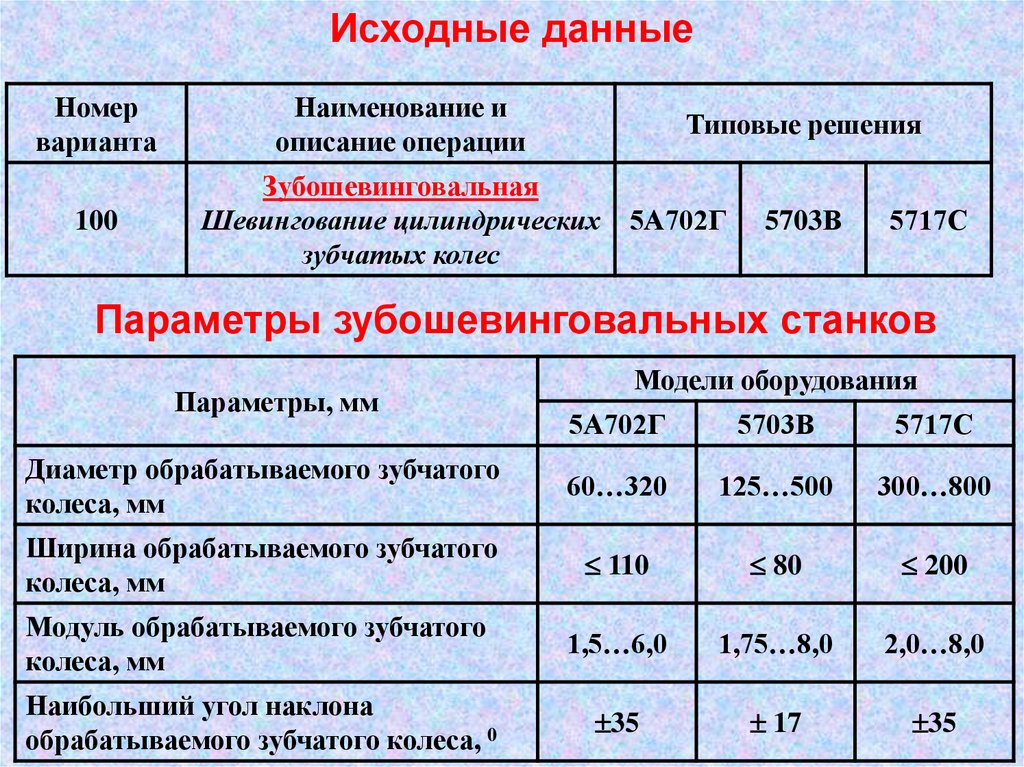
1. Исходные данные

Номер
варианта
Наименование и
описание операции
100
Зубошевинговальная
Шевингование цилиндрических
зубчатых колес
Типовые решения
5А702Г
5703В
5717С
Параметры зубошевинговальных станков
Параметры, мм
Модели оборудования
5А702Г
5703В
5717С
Диаметр обрабатываемого зубчатого
колеса, мм
60…320
125…500
300…800
Ширина обрабатываемого зубчатого
колеса, мм
110
80
200
Модуль обрабатываемого зубчатого
колеса, мм
1,5…6,0
1,75…8,0
2,0…8,0
Наибольший угол наклона
обрабатываемого зубчатого колеса, 0
35
17
35

2.

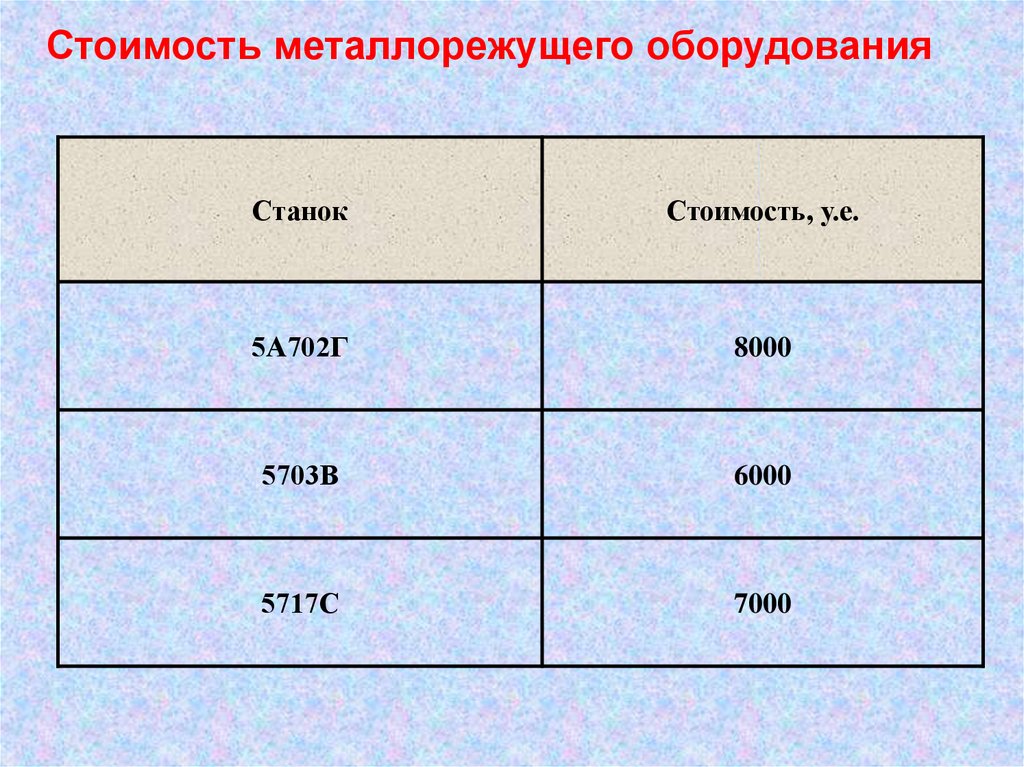
Стоимость металлорежущего оборудования
Станок
Стоимость, у.е.
5А702Г
8000
5703В
6000
5717С
7000

3. 1. Формируем множество типовых решений

МТР = {5А702Г, 5703В, 5717С}
2. Сформулируем условия применимости и комплекс
параметров применимости
Условия применимости:
1. Размещаемость детали в рабочей зоне станка. Диаметр зубчатого
колеса DД и его ширина LД должны находиться в пределах, допустимых
рабочей зоной станка.
2. Диапазоны допустимого изменения модуля зубчатого колеса mД и угла
наклона зуба детали αД.
Комплекс условий применимости
(КУП):
Dmin D Д Dmax
Lmin L Д Lmax
КУП
m
m
m
Д
max
min
min
Д
max
Комплекс параметров
применимости (КПП):
КПП ={DД, LД, mД, Д }

4.

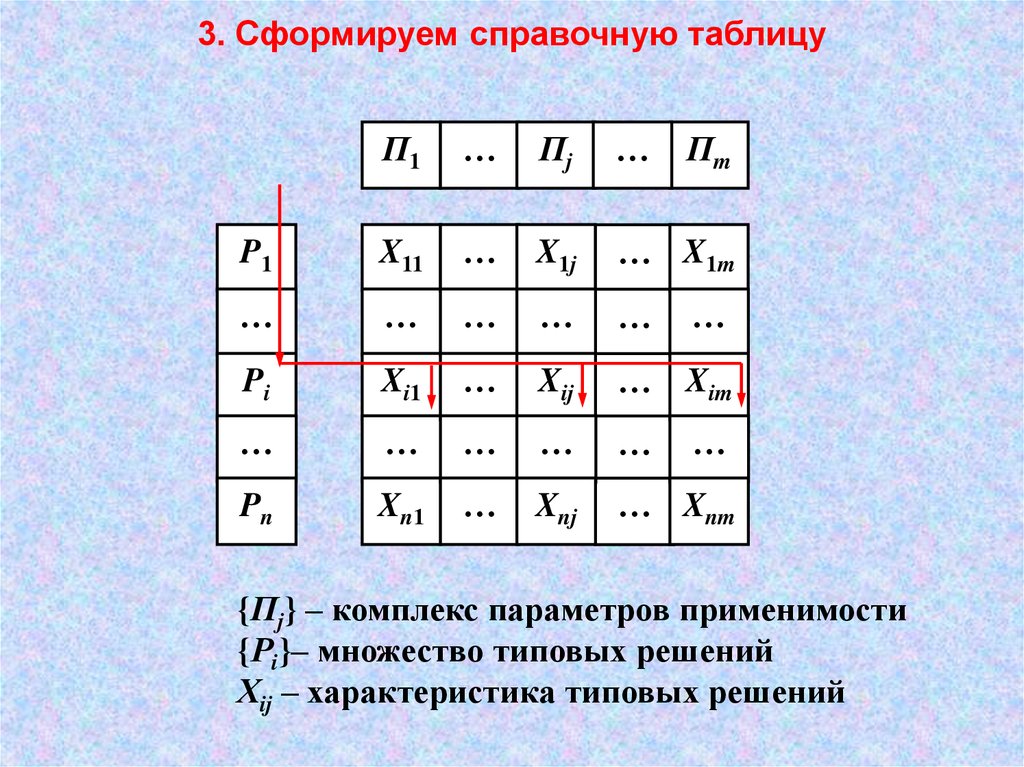
3. Сформируем справочную таблицу
П1
…
Пj
…
Пm
P1
X11
…
X1j
… X1m
…
…
…
…
…
Pi
Xi1
…
Xij
… Xim
…
…
…
…
…
Pn
Xn1
…
Xnj
… Xnm
…
…
{Пj} – комплекс параметров применимости
{Рi}– множество типовых решений
Хij – характеристика типовых решений

5.

Условия применимости зубошевинговальных станков
(справочная таблица)
Модель
станка
Параметры станков
DД, мм
LД, мм
mД, мм
Д, 0
5А702Г (Р1)
60…320
110
1,5…6,0
35
5703В (Р2)
125…500
80
1,75…8,0
17
5717С (Р3)
300…800
200
2,0…8,0
35

6.

4. Разработаем графические схемы выбора решений.
0
Р1
59
0
Р1, Р2
124
Р1
299
1,4
1,74
500
800
6,0
8,0
200
LД, мм
Р1, Р3
17
mД, мм
Р3
110
DД, мм
Р2, Р3
Р1, Р3
80
Р3
Р1, Р2, Р3
1,9
Р1, Р2, Р3
0
Р2, Р3
320
Р1, Р2
Р1, Р2, Р3
0
Р1, Р2, Р3
35
Д, 0

7.

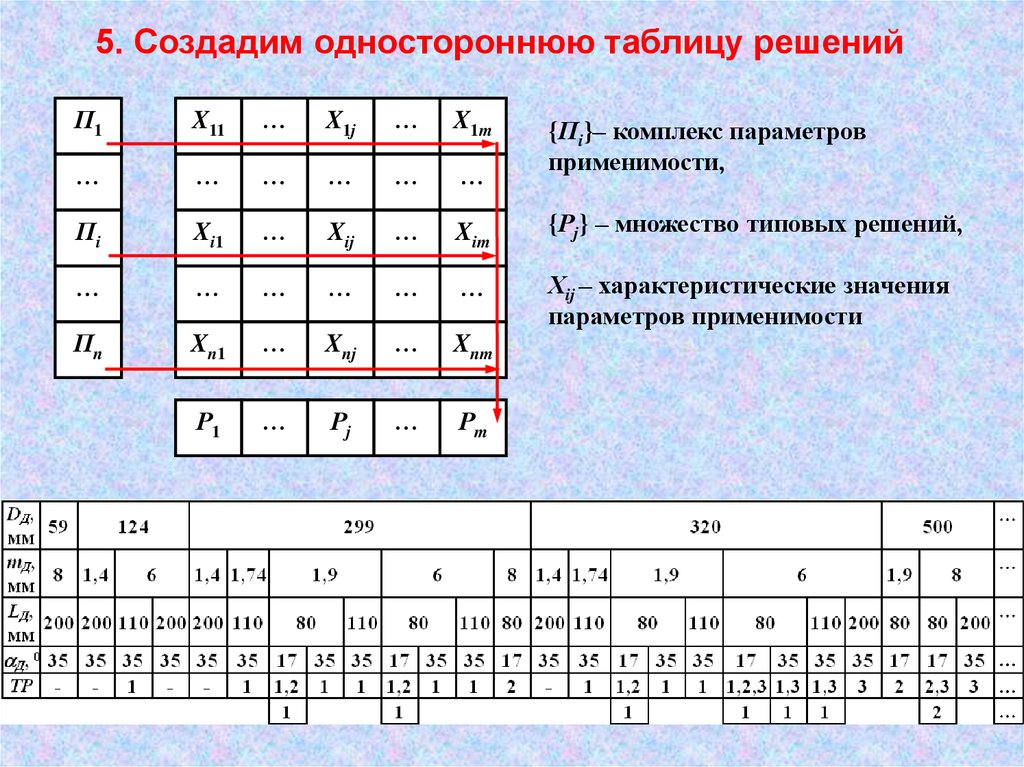
5. Создадим одностороннюю таблицу решений
П1
X11
…
X1j
…
X1m
…
…
…
…
…
…
Пi
Xi1
…
Xij
…
Xim
…
…
…
…
…
…
Пn
Xn1
…
Xnj
…
Xnm
Р1
…
Рj
…
Рm
{Пi}– комплекс параметров
применимости,
{Рj} – множество типовых решений,
Хij – характеристические значения
параметров применимости

8.

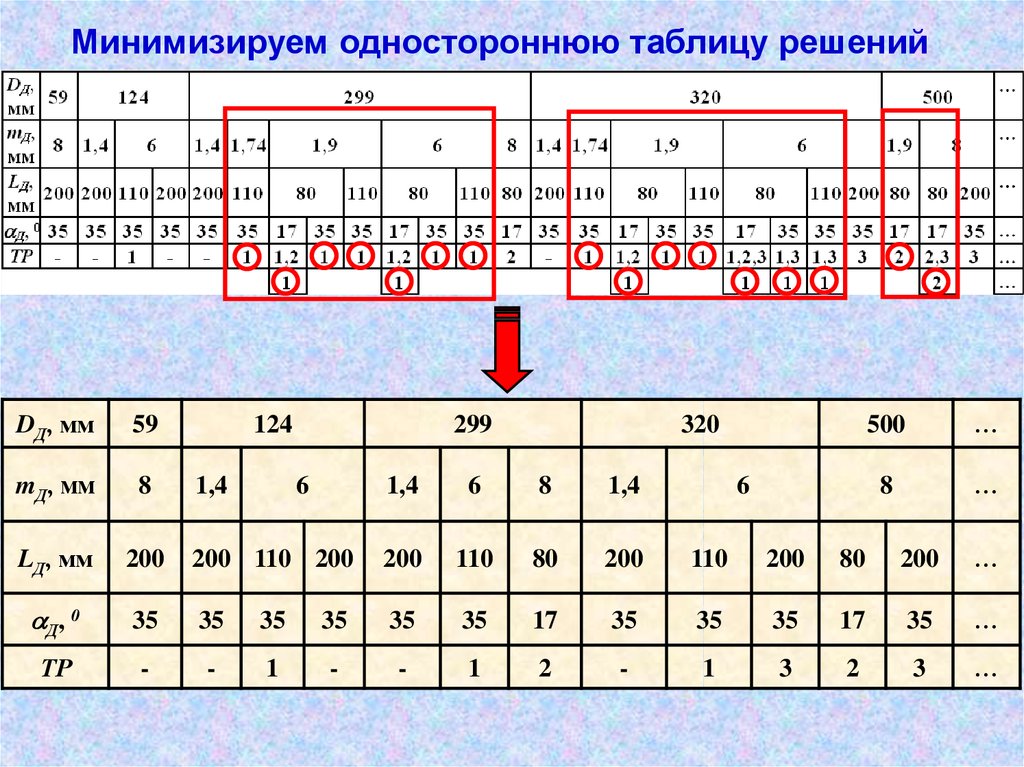
Минимизируем одностороннюю таблицу решений
DД, мм
59
mД, мм
8
LД, мм
200
Д, 0
ТР
124
1,4
299
6
320
6
500
…
8
…
1,4
6
8
1,4
200 110 200
200
110
80
200
110
200
80
200
…
35
35
35
35
35
35
17
35
35
35
17
35
…
-
-
1
-
-
1
2
-
1
3
2
3
…

9.

6. Преобразуем одностороннюю таблицу решений
в матрицу решений, удобную для обработки на ЭВМ
(формализуем одностороннюю таблицу решений)
DД, мм
59
124
124
124
299
299
299
320
320
320
500
500
…
mД, мм
8
1,4
6
6
1,4
6
8
1,4
6
6
8
8
…
LД, мм
200
200
110
200
200
110
80
200
110
200
80
200
…
Д, 0
35
35
35
35
35
35
17
35
35
35
17
35
…
ТР
0
0
1
0
0
1
2
0
1
3
2
3
…

10.

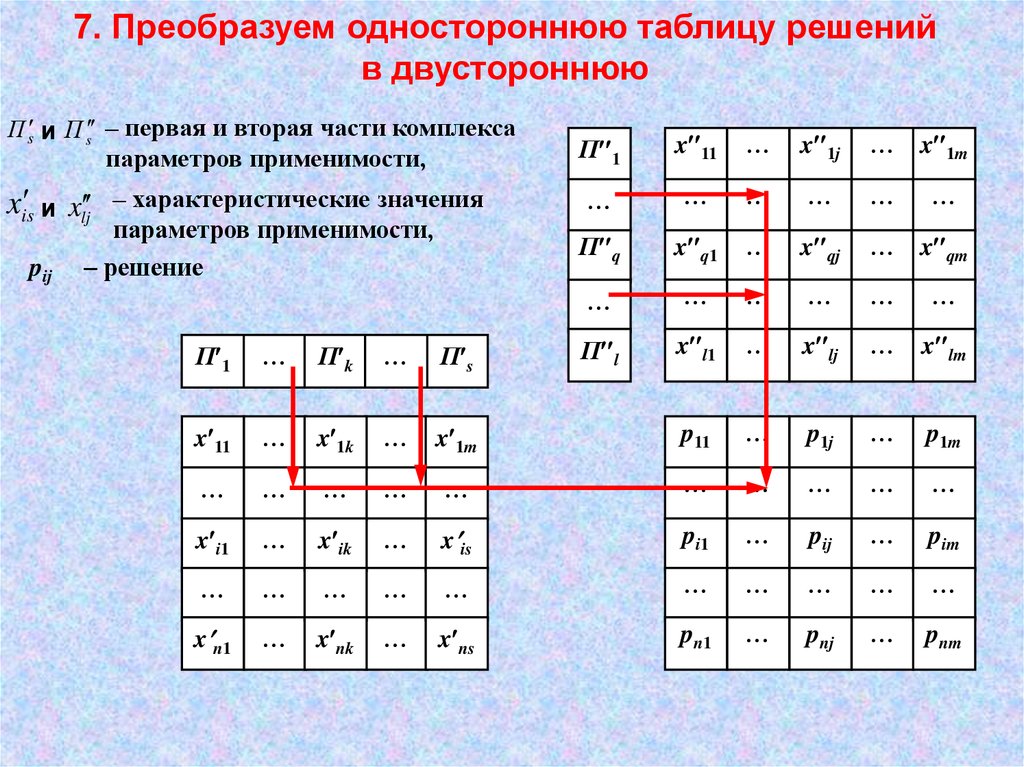
7. Преобразуем одностороннюю таблицу решений
в двустороннюю
П s и П s – первая и вторая части комплекса
параметров применимости,
xis и xlj
pij
– характеристические значения
параметров применимости,
– решение
П 1
x 11
…
x 1j
… x 1m
…
…
…
…
…
П q
x q1
…
x qj
… x qm
…
…
…
…
…
…
П l
x l1
…
x lj
…
x lm
…
П 1
…
П k
…
П s
x 11
…
x 1k
…
x 1m
p11
…
p1j
…
p1m
…
…
…
…
…
…
…
…
…
…
x i1
…
x ik
…
x is
pi1
…
pij
…
pim
…
…
…
…
…
…
…
…
…
…
x n1
…
x nk
…
x ns
pn1
…
pnj
…
pnm

11.

mД, мм при DД, мм
LД,
мм
80
110
200
Д, 0
59
124
299
320
500
…
8
1,4
6
1,4
6
8
1,4
6
8
…
17
-
-
-
-
-
1
-
-
2
…
35
-
-
-
-
-
-
-
-
-
…
17
-
-
-
-
-
-
-
-
-
…
35
-
-
1
-
1
-
-
1
-
…
17
-
-
-
-
-
-
-
-
-
…
35
-
-
-
-
-
-
-
3
3
…

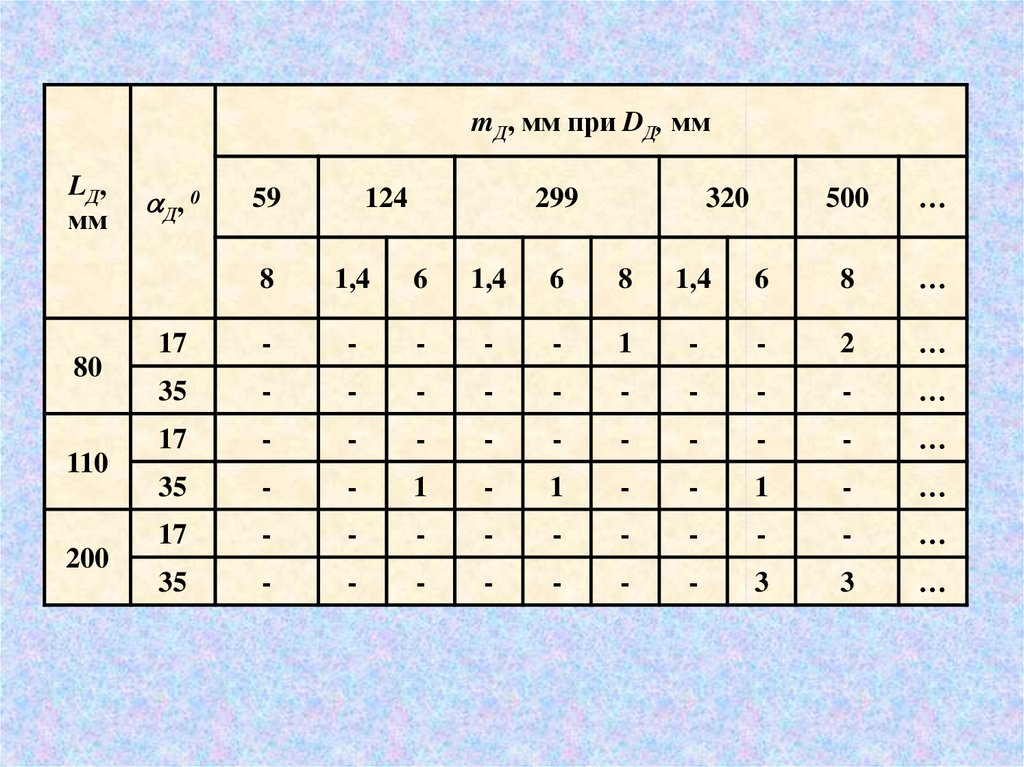
12.

Формализуем двустороннюю таблицу решений
mД, мм при DД, мм
LД,
мм
Д, 0
59
124
299
320
500
…
8
1,4
6
1,4
6
8
1,4
6
8
…
80
17
0
0
0
0
0
1
0
0
2
…
110
35
0
0
1
0
1
0
0
1
0
…
200
35
0
0
0
0
0
0
0
3
3
…

13.

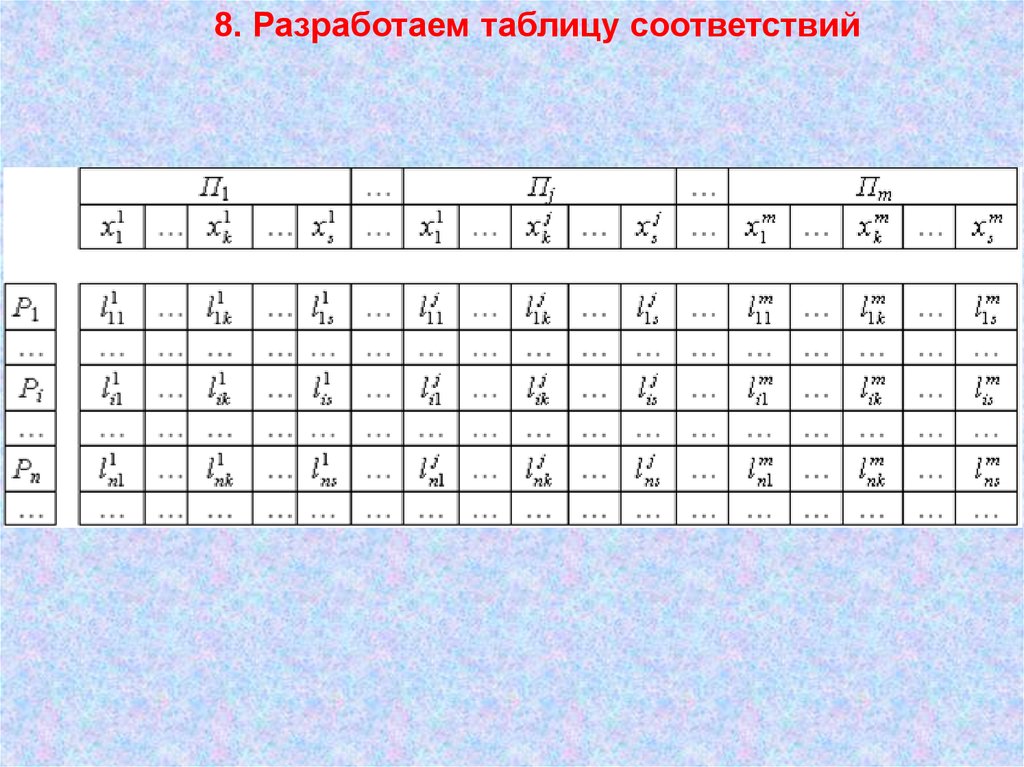
8. Разработаем таблицу соответствий

14.

15.

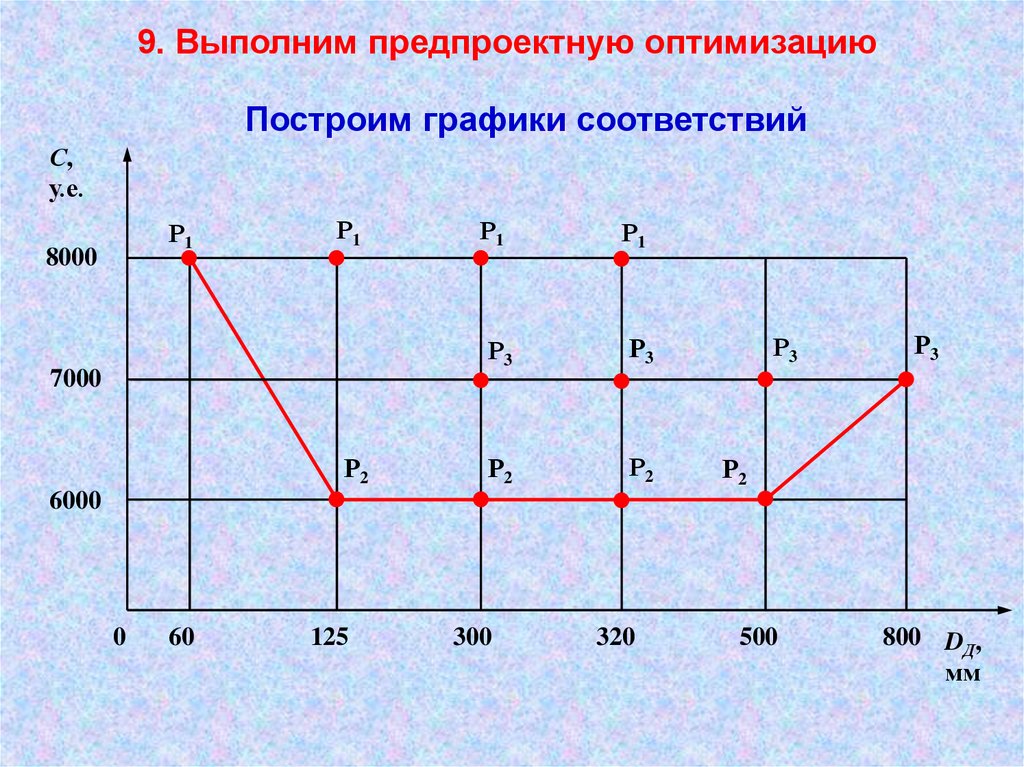
9. Выполним предпроектную оптимизацию
Построим графики соответствий
С,
у.е.
Р1
8000
Р1
Р1
Р1
Р3
Р3
Р2
Р2
Р3
Р3
7000
Р2
Р2
6000
0
60
125
300
320
500
800 DД,
мм

16.

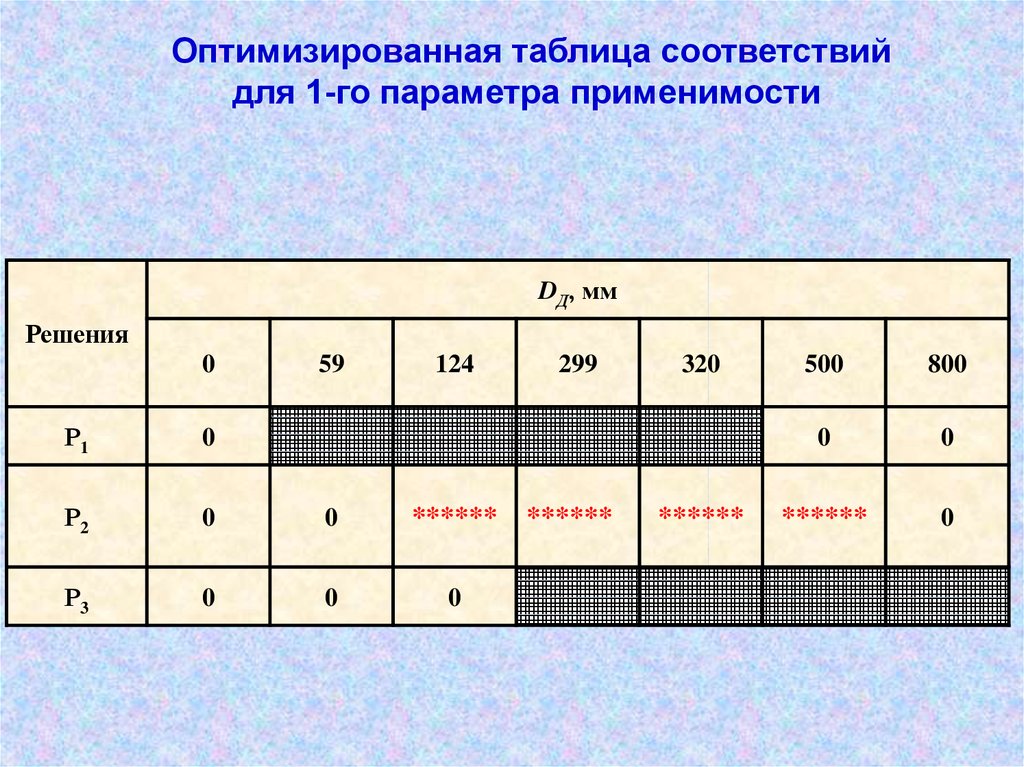
Оптимизированная таблица соответствий
для 1-го параметра применимости
DД, мм
Решения
0
59
124
Р1
0
Р2
0
0
******
Р3
0
0
0
299
******
320
******
500
800
0
0
******
0

17.

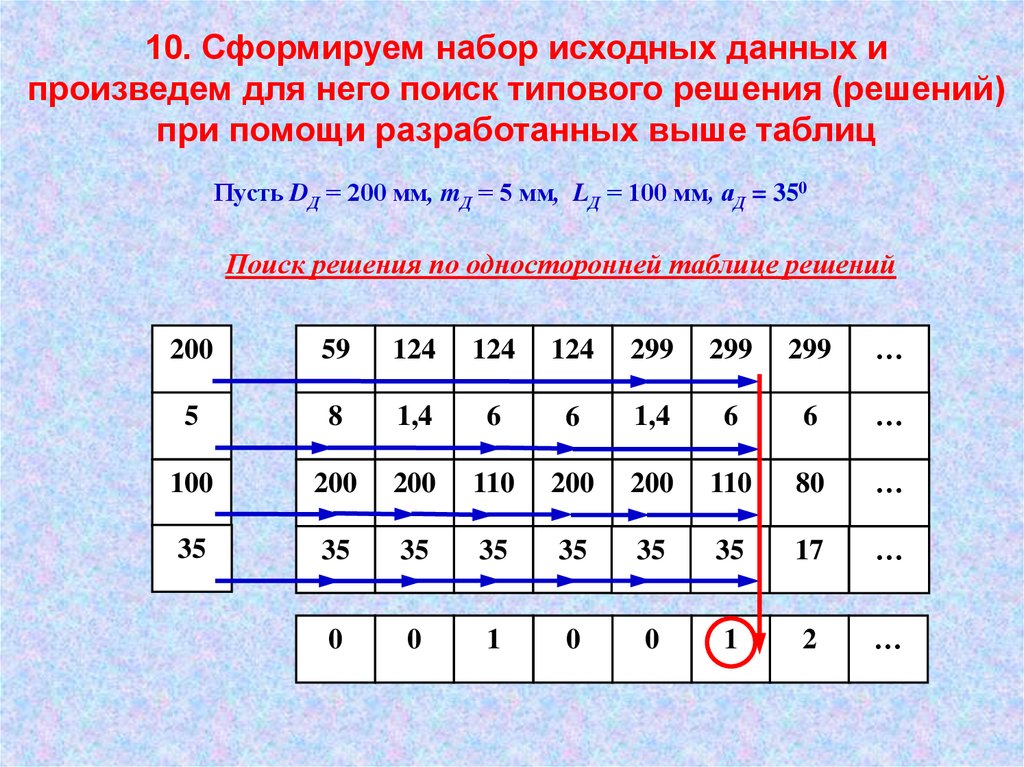
10. Сформируем набор исходных данных и
произведем для него поиск типового решения (решений)
при помощи разработанных выше таблиц
Пусть DД = 200 мм, mД = 5 мм, LД = 100 мм, аД = 350
Поиск решения по односторонней таблице решений
200
59
124
124
124
299
299
299
…
5
8
1,4
6
6
1,4
6
6
…
100
200
200
110
200
200
110
80
…
35
35
35
35
35
35
35
17
…
0
0
1
0
0
1
2
…

18.

Поиск решения по двусторонней таблице решений
124 299… 299
200
59
124
5
8
1,4
6
1,4
299
…
6
8
…
100
35
80
17
0
0
0
0
0
1
…
110
35
0
0
1
0
1
0
…
200
35
0
0
0
0
0
0
…

19.

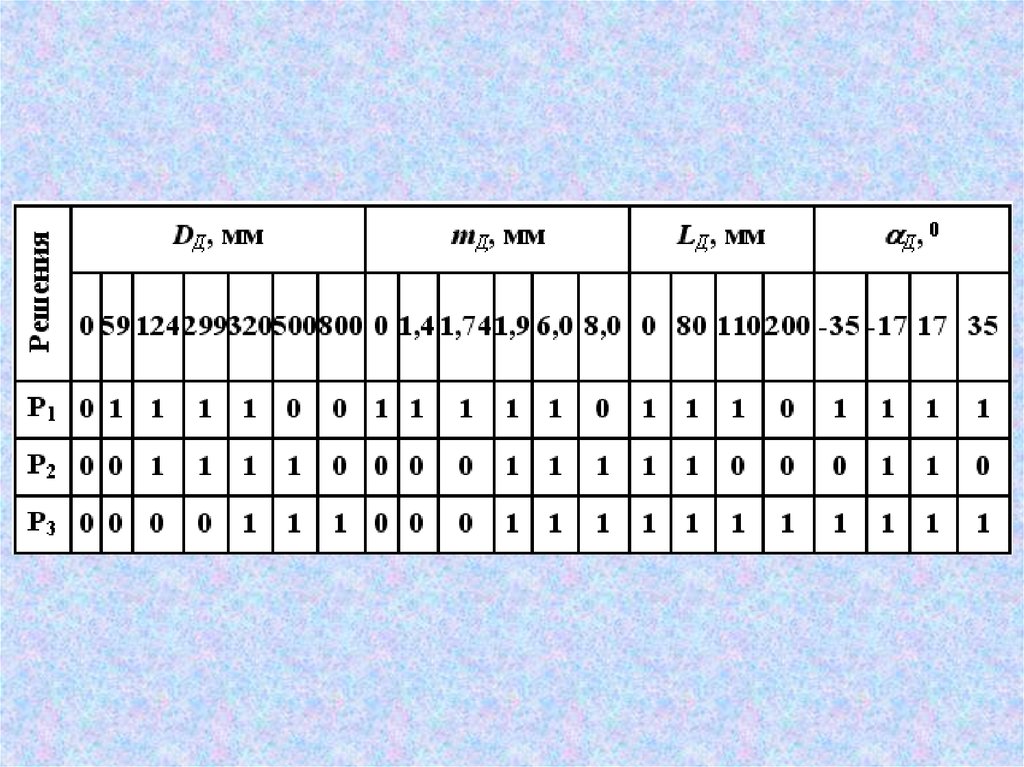
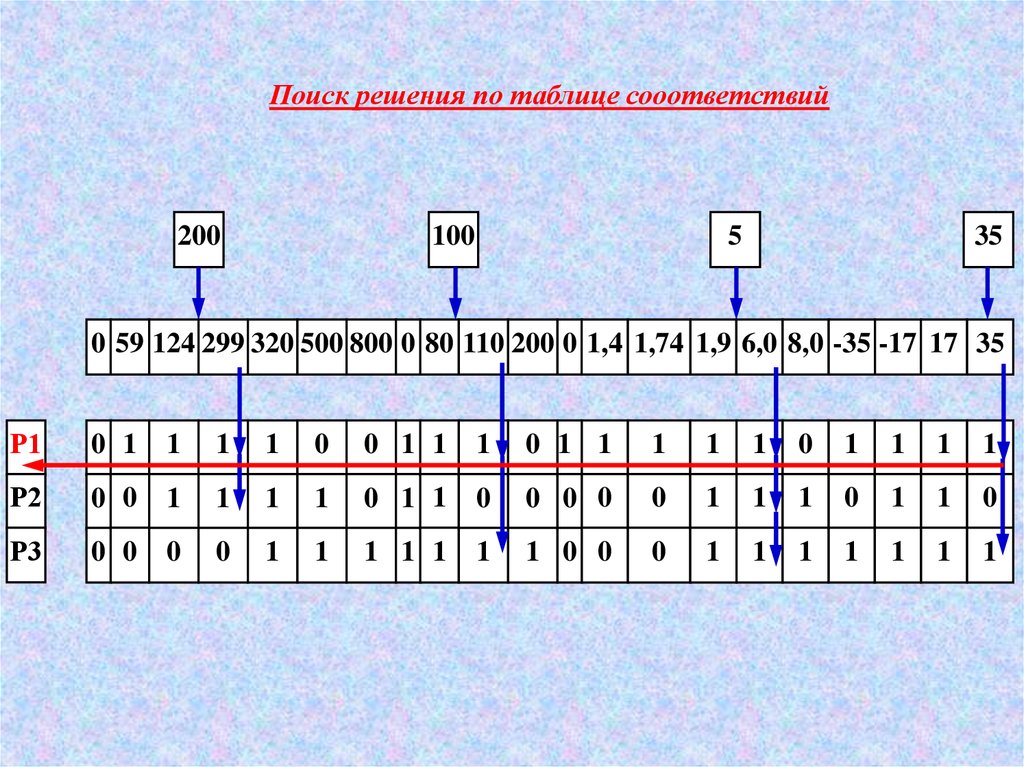
Поиск решения по таблице сооответствий
200
100
5
35
0 59 124 299 320 500 800 0 80 110 200 0 1,4 1,74 1,9 6,0 8,0 -35 -17 17 35
Р1
0 1
1
1
1
0
0 1 1
1
0 1 1
1
1
1
0
1
1
1
1
Р2
0 0
1
1
1
1
0 1 1
0
0 0 0
0
1
1
1
0
1
1
0
Р3
0 0
0
0
1
1
1 1 1
1
1 0 0
0
1
1
1
1
1
1
1