Похожие презентации:
Квадратное уравнение и его корни. 9 класс
1. Квадратное уравнение и его корни.
Учитель Куликова Л.А.9 класс.
2. Словарная работа.
Квадратное уравнение;неполное квадратное уравнение;
коэффициенты;
приведённое квадратное уравнение;
дискриминант;
корни уравнения;
формула корней квадратного уравнения.
3. Определение квадратного уравнения.
Квадратным уравнением называетсяуравнение вида ах2 + bх + с = 0, где х –
переменная, а, b и с - некоторые числа,
причем а 0.
Числа а, b и с - коэффициенты квадратного
уравнения.
Число
а
называют
первым
коэффициентом, b – вторым коэффициентом
и с – свободным членом.
4. Определение неполного квадратного уравнения.
Если в квадратном уравнении ах2 + bх + с = 0 хотя быодин из коэффициентов b или с равен нулю, то
такое уравнение называют неполным квадратным
уравнением.
Виды неполных квадратных уравнений:
1) ах2 + с = 0; где с≠0;
2) ах2 + bх = 0; где b≠0
3) ах2 = 0
5. Дискриминант квадратного уравнения.
«Дискриминант» по латыни - различитель.Дискриминантом квадратного уравнения ах2 +
bх + с = 0 называется выражение b2 – 4ac.
Его обозначают буквой D, т.е. D= b2 – 4ac.
Возможны три случая:
D 0
D 0
D 0
6. Если D 0
Если D 0В этом случае уравнение ах2 + bх + с = 0
имеет два действительных корня:
b D
x1
2a
b D
и x2
.
2a
7. Если D = 0
В этом случае уравнение ах2 + bх + с = 0имеет один действительный корень:
b 0
x
2a
b
x
2a
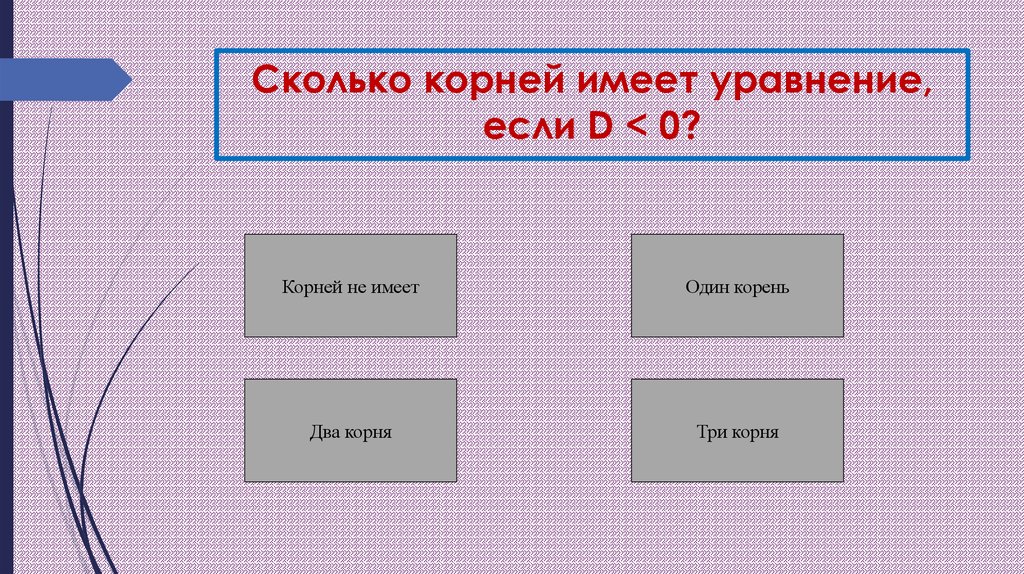
8. Если D 0
Если D 0Уравнение ах2 + bх + с = 0 не имеет
корней.
9. Формула корней квадратного уравнения.
b D2
x1,2
, где D b 4ac.
2a
10. Определение приведенного квадратного уравнения
Приведенным квадратнымуравнением называется квадратное
уравнение, первый коэффициент
которого равен 1.
х2 + bх + с = 0
11. План решения квадратных уравнений.
Найдите дискриминант.Определите число корней квадратного
уравнения.
Найдите корни (корень) по
соответствующей формуле (если эти
корни есть).
Запишите ответ.
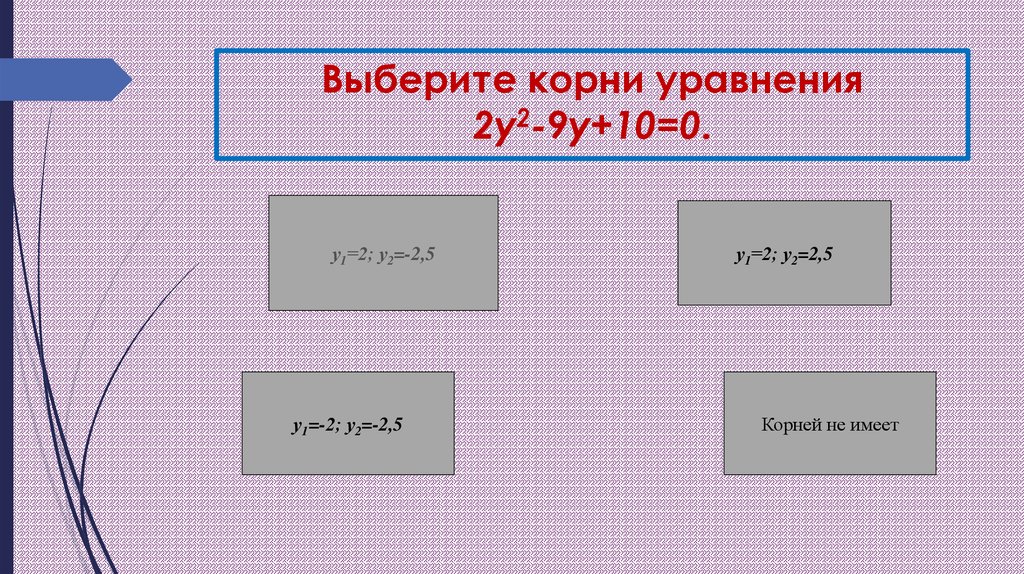
12. Задание.
Решите уравнение:2x2- 5x - 3 = 0.
2x2- 3x + 5 = 0.
x2+ 2x + 1 = 0.
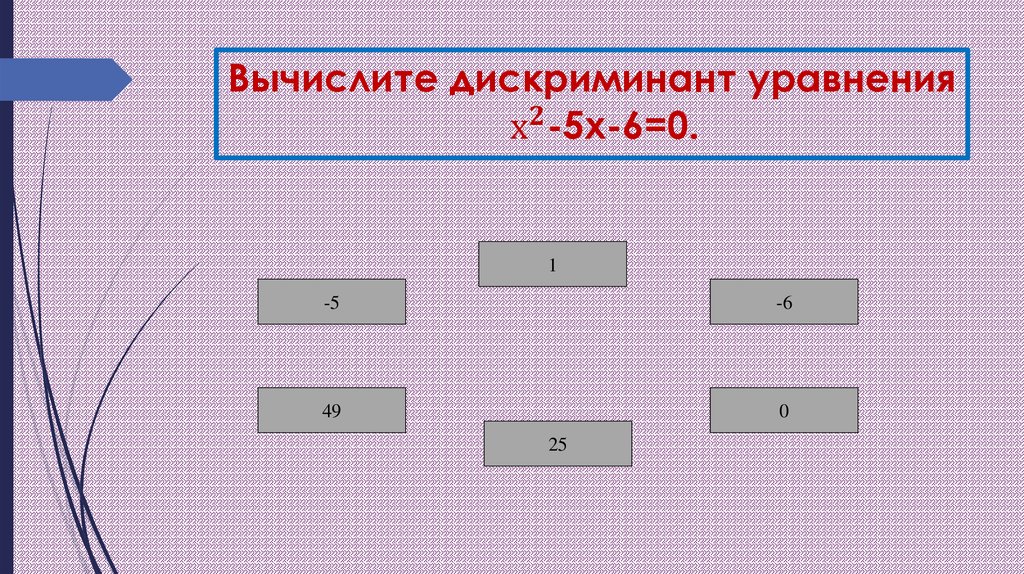
13. Вычислите дискриминант уравнения х^2-5х-6=0.
Вычислите дискриминант уравнениях













 Математика
Математика








