Графическое решение квадратных уравнений

1. Графическое решение квадратных уравнений

Е.В.Кирина
учитель математики
МАОУ «Центр образования 13 имени Героя
Советского Союза Н.А.Кузнецова»
г.Тамбов

2. Цель урока

• формировать умение решать
квадратные уравнения графическим
способом.

3. Решить уравнение х2 – 2х –3 = 0

Решение.
I способ
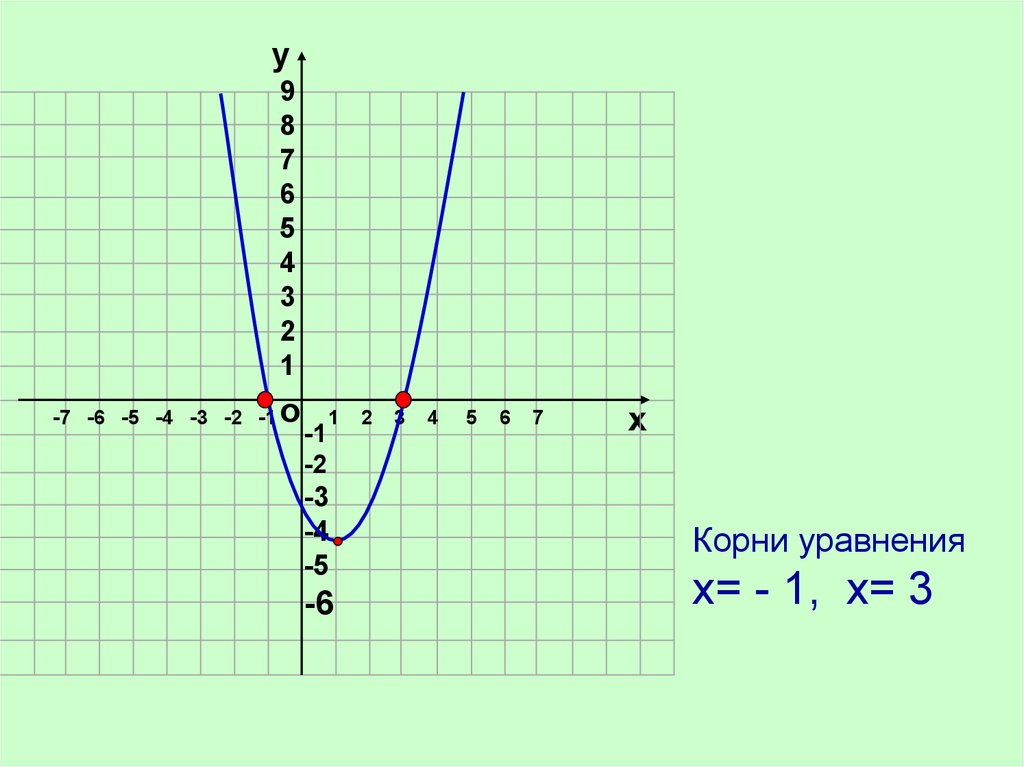
Построим график функции у = х2 – 2х –3
Найдём координаты вершины параболы:
Х0= - в = 1
2а
у0 = - 4
Значит, (1; - 4) –вершина параболы
Х = 1 ось симметрии параболы

4.

• Возьмём на оси х две точки,
симметричные относительно оси
параболы, например, точки х = - 1 и х = 3.
Имеем: f(- 1) = f(3) = 0.
• Отметим на координатной плоскости
точки (- 1; 0), (1; - 4), (3; 0) и через эти
точки проведём параболу

5.

у
9
8
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
о
-1
-2
1
-3
-4
-5
-6
2
3
4
5
6
7
х
Корни уравнения
х= - 1, х= 3

6.

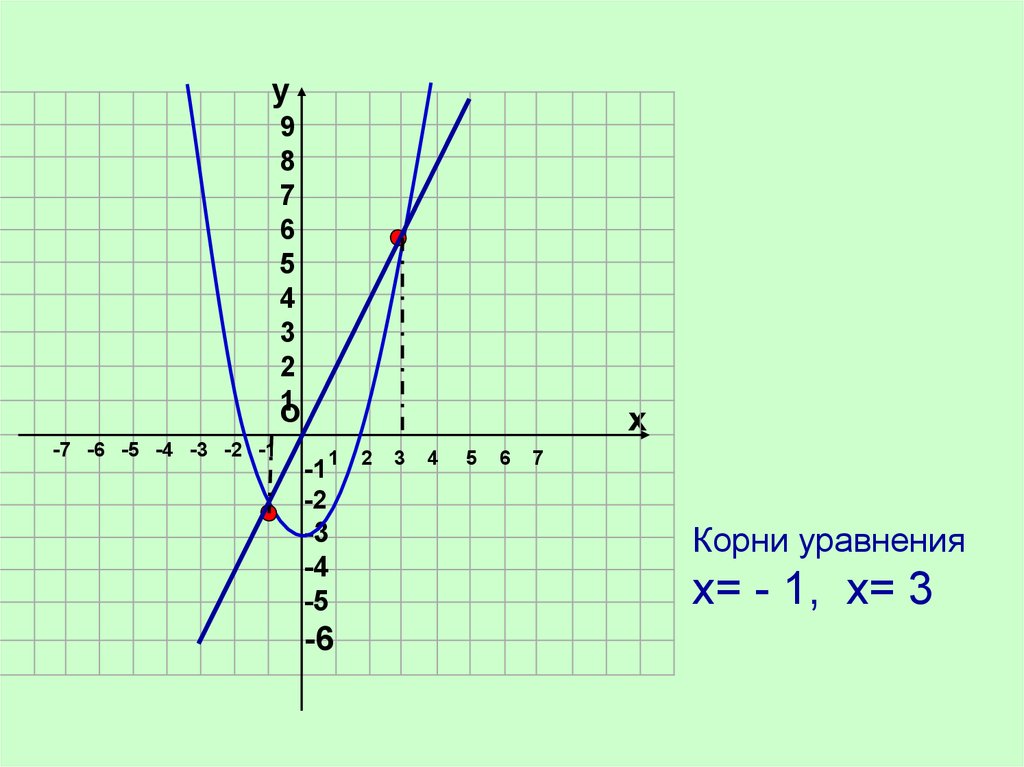
II способ
Преобразуем уравнение к виду х2 = 2х +3.
Построим в одной системе координат графики
функций у = х2 и у = 2х + 3.
Графики пересекаются в двух точках А(- 1; 1) и
В(3; 9). Корнями уравнения служат абсциссы
точек А и В, т.е. х1 = - 1, х2 = 3.

7.

у
9
8
7
6
5
4
3
2
1
о
-7 -6 -5 -4 -3 -2 -1
х
-1 1
-2
-3
-4
-5
-6
2
3
4
5
6
7
Корни уравнения
х= - 1, х= 3

8.

III способ
Преобразуем к виду х2 – 3 = 2х.
Построим в одной системе координат графики
Функций у = х2 – 3 и у = 2х.
Они пересекаются в двух точках А(- 1; - 2) и
В(3; 6). Корнями уравнения являются абсциссы
точек А и В, т.е. х1 = - 1, х2 = 3.

9.

у
9
8
7
6
5
4
3
2
1
о
-7 -6 -5 -4 -3 -2 -1
х
-1 1
-2
-3
-4
-5
-6
2
3
4
5
6
7
Корни уравнения
х= - 1, х= 3

10.

IV способ
Преобразуем уравнение к виду х2 – 2х + 1 - 4 = 0
и далее х2 – 2х + 1 = 4, т.е. (х - 1)2 = 4.
Построим в одной системе координат параболу
у = (х - 1)2 и прямую у = 4.
Они пересекутся в двух точках А(- 1; 4) и В(3; 4).
Корнями уравнения являются абсциссы точек
А и В, х1 = - 1, х2 = 3.

11.

у
9
8
7
6
5
4
3
2
1
о
-7 -6 -5 -4 -3 -2 -1
х
-1 1
-2
-3
-4
-5
-6
2
3
4
5
6
7
Корни уравнения
х= - 1, х= 3

12.

V способ
Разделив почленно обе части уравнения на х
3
3
получим: х – 2 –
= 0; х – 2 = .
х
х
Построим в одной системе координат гиперболу
3
у=
и прямую у = х – 2.
х
Они пересекаются в двух точках А(- 1; - 3) и
В(3; 1).
Корнями уравнения являются абсциссы точек
А и В, х1 = - 1, х2 = 3.

13.

7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
Корни уравнения
х= - 1, х= 3
-1 1 2 3 4 5 6 7
-2
-3
-4
-5
-6
-7

14. Вывод

Квадратное уравнение х2 – 2х –3 = 0
можно решить графически пятью способами.
На практике вы может выбирать любой
понравившийся способ, но следует отметить,
что сто процентную гарантию решения
квадратного уравнения графический способ
не даёт.

15. Решите самостоятельно

Решите графически уравнение
- х2 - 5х –6 = 0
(любым понравившимся способом)
Ответ: - 3; - 2

16. Домашнее задание

П. 23 № 23.5(а,б)
№ 23.7(а,б)
№ 23.8(а)