Похожие презентации:
Способы решения квадратного уравнения
1. СПОСОБЫ РЕШЕНИЯ КВАДРАТНОГО УРАВНЕНИЯ
2. СОДЕРЖАНИЕ
• Графическое решение квадратногоуравнения
• Свойства коэффициентов
квадратного уравнения
• Решение уравнения способом
«переброски»
• Метод выделения полного квадрата
3. ГРАФИЧЕСКОЕ РЕШЕНИЕ КВАДРАТНОГО УРАВНЕНИЯ
1. Записать уравнение ах²+bх+с=0 ввиде х =-bх-с;
2. Построить параболу y=х , и
прямую y=-bх-с ;
3. Найти точки пересечения ;
4. Записать ответ.
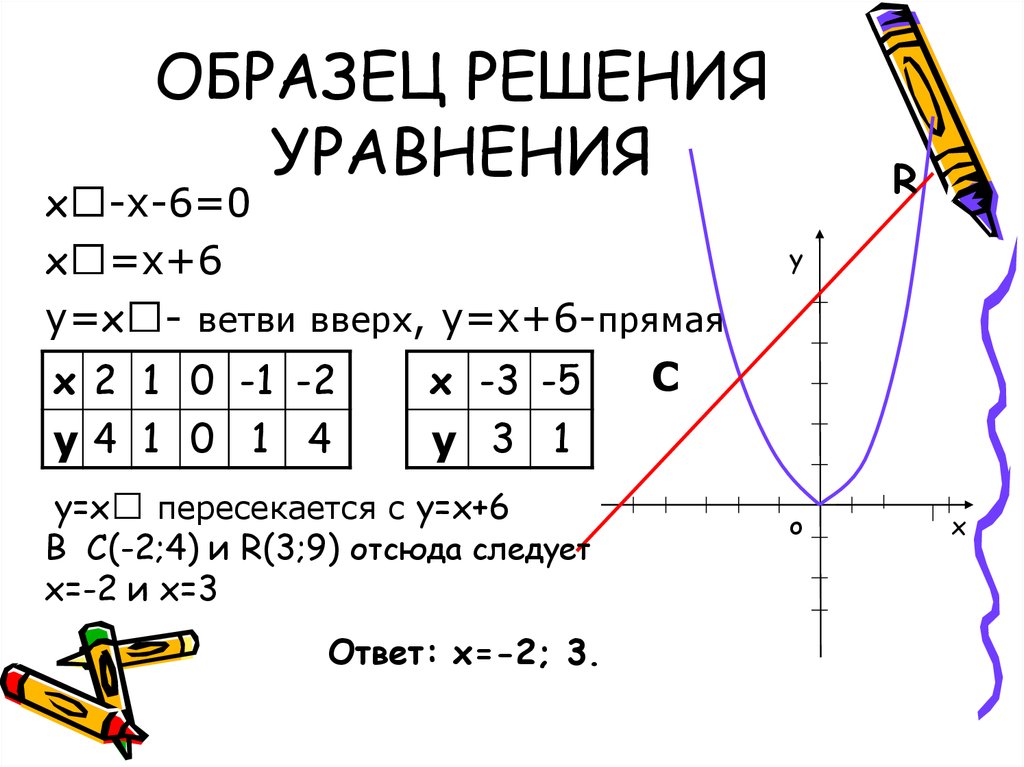
4. ОБРАЗЕЦ РЕШЕНИЯ УРАВНЕНИЯ
х -х-6=0х =х+6
y=х - ветви вверх, y=х+6-прямая
С
х 2 1 0 -1 -2
х -3 -5
y4 1 0 1 4
R
y
y 3 1
y=х пересекается с y=х+6
В С(-2;4) и R(3;9) отсюда следует
х=-2 и х=3
Ответ: х=-2; 3.
o
x
5. СВОЙСТВА КОЭФФИЦЕНТОВ КВАДРАТНОГО УРАВНЕНИЯ
ах²+bх+с=0, где а≠01. Если а+b+с=0,
то х1=1, х2=с:а
2. Если а-в+с=0,
то х1=-1, х2=-с:а
6. ОБРАЗЕЦ РЕШЕНИЯ УРАВНЕНИЯ
1) 5х -7х+2=0 , так кака+b+с=0, то х1=1, х2=с:а=0,4
Ответ: х1=1, х2=0,4
2) 6х +9х+3=0, так как
а-в+с=0, то х1=-1, х2=-с:а=-0,5
Ответ: х1=-1, х2=-0,5
7. РЕШЕНИЕ УРАВНЕНИЯ СПОСОБОМ «ПЕРЕБРОСКИ»
ах²+bх+с=0 , где а≠0Умножаем уравнение на а
a²х²+abх+ac=0
Пусть aх=y, тогда y²+by+ac –
равносильны =>
х1 =y1: а , х2 =y2 : а
8. ОБРАЗЕЦ РЕШЕНИЯ УРАВНЕНИЯ
2х -9х+9=0y -9y+18=0
y1*y2=18, y1=3, х1=1,5,
y1+y2=9 ; y2=6; х2=3 ;
Ответ: х1=1,5 ; х2=3.
9. МЕТОД ВЫДЕЛЕНИЯ ПОЛНОГО КВАДРАТА
х+6х-7=0
Представим х
+6х в виде квадратов
суммы двух выражений.
х +6х=х +2х3
х +2х3+3 =(х+3)
х +6х-7=х +2*х*3+3
(х+3) -16
-3 =








 Математика
Математика








