Похожие презентации:
Методы решения квадратных уравнений
1. Исследовательская работа по теме: «Методы решения квадратных уравнений»
Выполнил:ученик 9 класса
Иванютин Артём
Руководитель:
учитель математики
Нечаева Елена Николаевна
2.
Стоит только показать,что какая-либо вещь
невозможна,
как найдется математик,
который ее сделает.
(У. У. Сойер)
3. Квадратные уравнения
Полные ах² + bх + с = 0где а≠0
Приведённые х²+bх+с=0 где а=1
Виды
Неполные ах²+с=0 где b=0
Неполные ах²+bх =0 где c=0
Неполные ах²=0 где b=0 и c=0
Уравнения, приводимые к квадратным
4. Методы решения квадратных уравнений
По формуламРазложение на множители
Методы
Выделение полного квадрата
По теореме Виета
Функционально-графический метод
Свойства коэффициентов
5. Решу квадратное уравнение Х2 -2х-3=0 разными методами
Решу квадратное уравнение2
Х -2х-3=0
разными методами
1. По формулам
Х2 -2х-3=0
Д= 4-4*1*(-3)= 4+12=16=42
х1 =(2+4):2 = 6:2=3
х2 =(2-4):2= -2:2=-1
Ответ: 3; -1
6. 2.Разложение на множители (способ группировки и вынесение общего множителя за скобки)
Х2 -2х-3=0Х2 – 3х+х -3=0
х(х-3) +(х-3)=0
(х-3)(х+1)=0
х-3=0 или х+1=0
х=3
х=-1
Ответ: 3; -1
7. 3.Выделение полного квадрата
Х2 -2х -3=0Х2 -2х+1 -1-3=0
(х-1)2 -4=0
(х-1)2 =4
х-1=2
х-1=-2
Х=3
х=-1
Ответ: 3; -1
8. 4.По теореме Виета
Х2 -2х-3=0Х 1 * Х 2 =-3 = -1 * 3
Х 1 + Х 2 = 2 = -1+3
Х 1 =3
Х 2 =-1
Ответ: 3; -1
9. 5. Функционально- графический метод Х2 -2х-3=0 у= Х2 у=2х+3
Ответ: -1;310. 6. По свойству коэффициентов квадратного уравнения
ах2 + bх + с = 0, а ≠ 01.Если а + b + с = 0 (т.е. сумма
коэффициентов уравнения равна
нулю),
то х1 = 1, х2 = с:а
2. Если а - b + с = 0, или b = а + с,
то х1 = – 1, х2 = – с:а
11.
Решить уравненияХ2 -2х-3=0
( a-b+c) 1+2-3=0 х1 = -1 х2 = -(-3:1)=3
Ответ: 3; -1
345х2 – 137х – 208 = 0.
(а + b + с = 0)
345-137-208=0
то х1 = 1, х2 = -208/345
Ответ: 1; -208/345
12. 7.Метод переброски старшего коэффициента
Корни квадратных уравнений связанысоотношением: (при Д≥0)
ах2 + bх + с = 0 и у2 + bу + ас = 0
Х1 =у1:а
Х2 =у2 :а
Пример: 2х2 - 9х - 5 = 0
у2 – 9у - 10 = 0 у1 =10 у2 =-1
Х1 = 10:2=5 Х2 = -1/2
Ответ: 5; -1/2
13. Ф.Ф.Лысенко 2016г
2х2 -5х-7=0а-b+c=0
2+5-7=0 х1 =-1 х2 = -(-7:2) = 3,5
Ответ: -1; 3,5
В -9 №4
х2 -3х-40=0
х1 х2 =- 40 = 8*(-5)
Х1 + х2 = 3 = 8+(-5)
х1 = 8 х2 = -5
Ответ: 8; -5
В -5 №4
14.
В -15 №42х2 -7х-15=0
у2 -7у-30=0
У1 * У2 =-30= 10*(-3)
У1 + У2 = 7 = 10+(-3)
У1 = 10 У2 = -3
х1 =10:2=5
Х2 = -3:2 = -1,5
Ответ: 5; -1,5
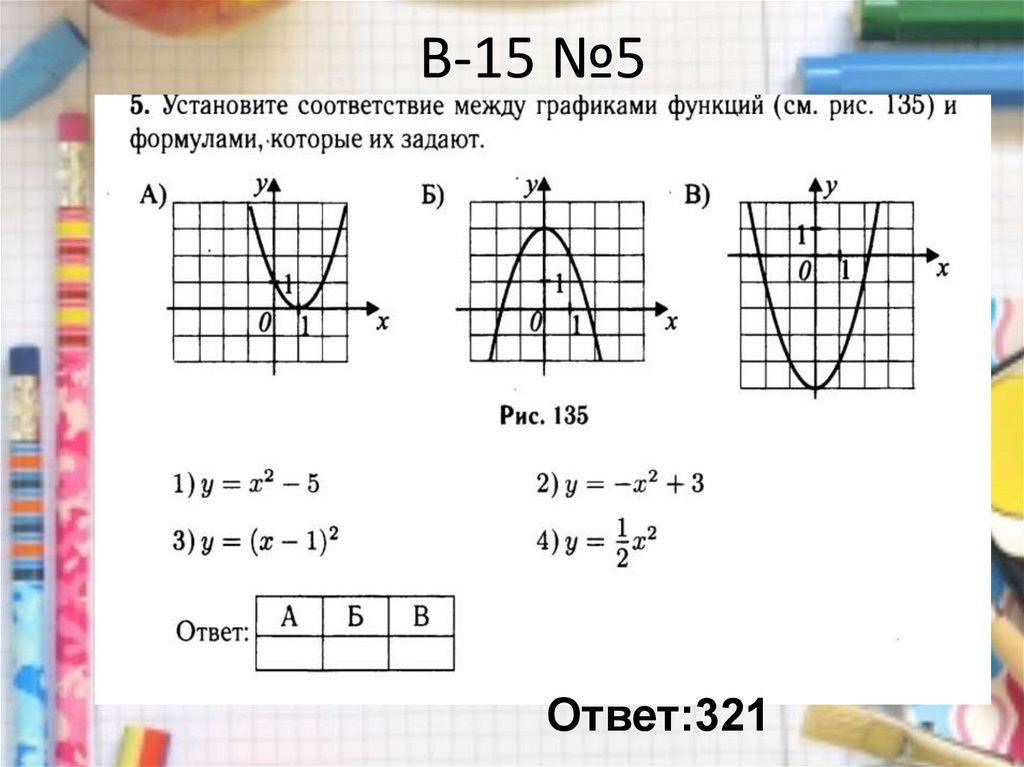
15. В-15 №5
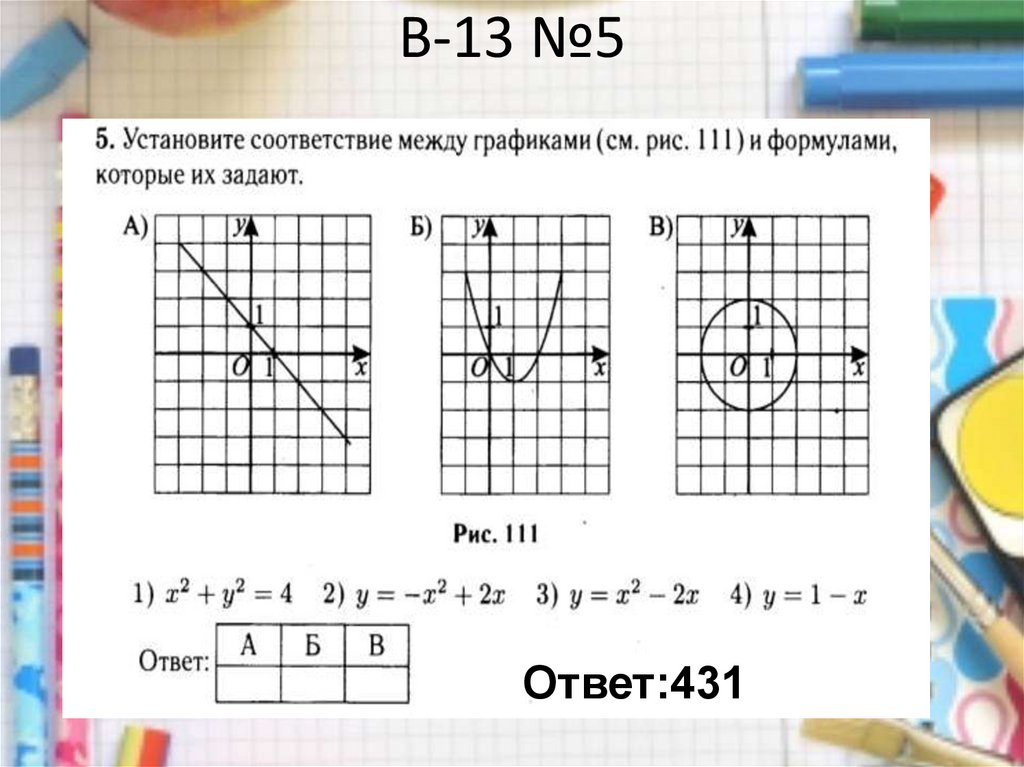
Ответ:32116. В-13 №5
Ответ:43117.
Для создания шаблона использованыресурсы сайта:
http://lenagold.ru/fon/main.htm
http://images.yandex.ru















 Математика
Математика








