Похожие презентации:
Задачи с экономическим содержанием
1. Задачи с экономическим содержанием
2. Задачи о вкладах и кредитовании
Проценты по вкладам (депозитам)Проценты по кредитам
3. Задачи оптимизации производства товаов и услуг
Логический перебор в задачахоптимизации
Линейные целевые функции с
целочисленными точками экстремума
Линейные целевые функции с
нецелочисленными точками
экстремума
Нелинейные целевые функции с
целочисленными точками экстремума
Нелинейные целевые функции с
нецелочисленными точками эстремума
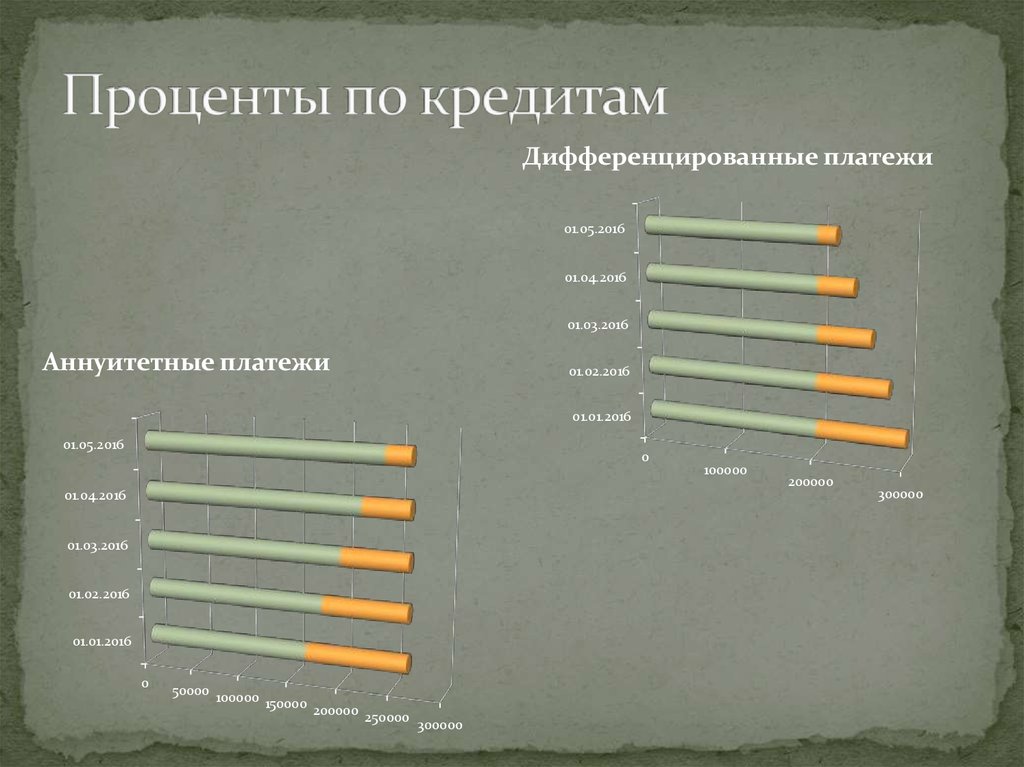
4. Проценты по кредитам
Дифференцированные платежи01.05.2016
01.04.2016
01.03.2016
Аннуитетные платежи
01.02.2016
01.01.2016
01.05.2016
0
01.04.2016
01.03.2016
01.02.2016
01.01.2016
0
50000 100000
150000 200000
250000 300000
100000
200000
300000
5. Дифференцированные платежи
Пусть S 0 - сумма кредита; n – число платежей, равноечислу платежных периодов; k% - годовой процент;
S 0 - фиксированная сумма
n
Рассчитаем проценты по кредиту:
kS0
w1
;
100
S0 k
kS0 n 1
w2 S 0
;
n 100
100n
2S k
kS n 2
w3 S 0 0
0
;
n 100
100n
3S k
kS n 3
w4 S 0 0
0
;
n 100
100n
(n 1) S 0 k
kS0
wn S 0
.
n
100 100n
6. Общая сумма w всех начисленных процентов (переплата) находится по формуле:
w w1 w2 w3 ... wnkS0 kS0 (n 1) kS0 (n 2) kS0 (n 3)
kS0
...
100
100n
100n
100n
100n
kS0
n n 1 n 2 n 3 ... 1
100n
kS0 1 n
kS0 (n 1)
n
100n 2
200
kS0 n 1
S S0
200
7.
15-го января планируется взять кредит в банке на 19 месяцев. Условия еговозврата таковы:
-1-го числа каждого месяца долг возрастает на r% по сравнению с концом
предудущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть
долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же сумму
меньше долга на 15-е число предыдущего месяца.
Известно. что общая сумма выплат после полного погашения кредита на
30% больше суммы взятой в кредит. Найдите r%
kS0 n 1
S S0
200
rS 0 (19 1)
20rS 0
rS 0
r
S S0
S0
S0
S 0 1
200
200
10
10
r
r
r
1,3
S 0 1 1,3S 0 1
0,3
100
10
100
r 3%
8. Аннуитетные платежи
Пусть S 0 - сумма кредита; n – число платежей, равноечислу платежных периодов; k% - годовой процент;
X – сумма регулярного платежа
Пусть m 1 k
100
Запишем суммы долга по истечении каждого
платёжного периода:
9.
S 1 S 0 S 0k
k
x S 0 1
x S 0 m x;
100
100
k
S 2 S1 S1
x S1m x ( S 0 m x)m x S 0 m 2 xm x;
100
S 3 S 2 m x S 0 m 2 xm x m x S0 m3 xm2 xm x;
S n S n 1m x S 0 m n xmn 1 ... xm x;
n 1
S n 0 S 0 m xm
n
... xm x 0
S 0 m n xmn 1 ... xm x
S 0 m n x m n 1 ... m 1
n
m
1
n
S0 m x
m 1
S 0 m n (m 1)
x
mn 1
10.
31 декабря 2013 года Сергей взял в банке 11 028 930рублей в кредит под 11% годовых. Схема выплаты
кредита следующая - 31 декабря каждого следующего
года банк начисляет проценты на оставшуюся сумму
долга (то есть увеличивает долг на 11%), затем Сергей
переводит в банк x рублей. какова должна быть
сумма x, чтобы Сергей выплатил долг тремя
равными платежами (то есть за три года).
S 0 m n (m 1)
x
mn 1
11028930 1,113 (1,11 1)
x
4513182,3( р)
3
1,11 1
11. Нелинейные целевые функции с целочисленными точками экстремума
12.
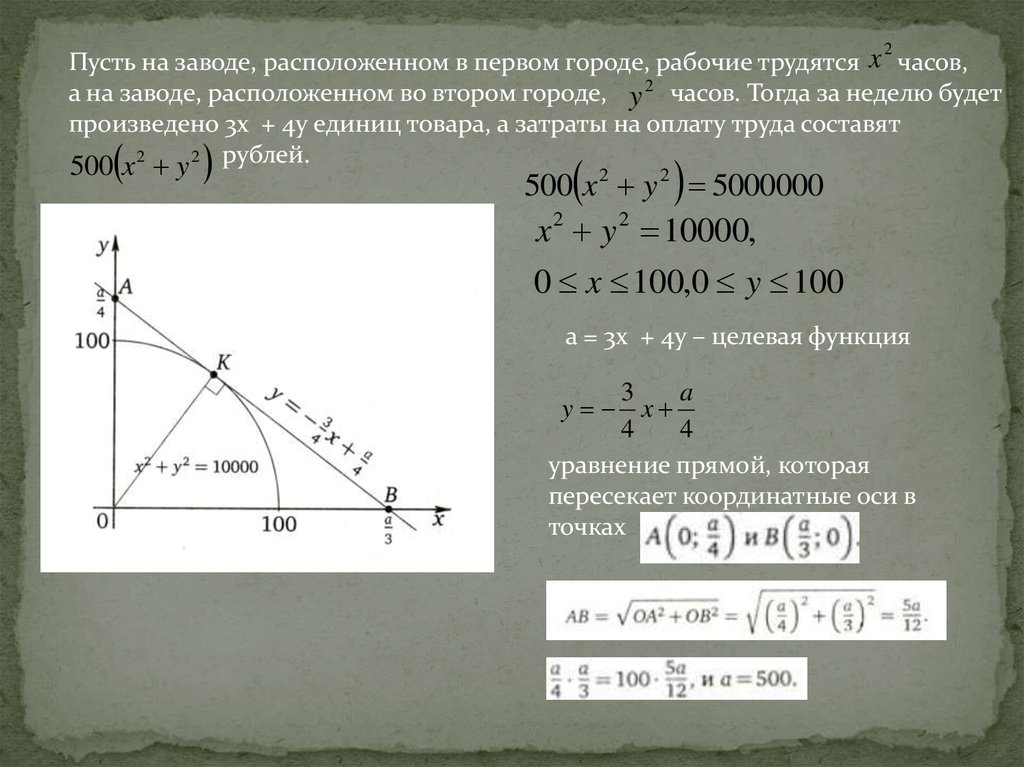
2Пусть на заводе, расположенном в первом городе, рабочие трудятся x часов,
а на заводе, расположенном во втором городе, y 2 часов. Тогда за неделю будет
произведено 3x + 4y единиц товара, а затраты на оплату труда составят
500 x 2 y 2 рублей.
500 x 2 y 2 5000000
x 2 y 2 10000,
0 x 100,0 y 100
a = 3x + 4y – целевая функция
3
a
y x
4
4
уравнение прямой, которая
пересекает координатные оси в
точках







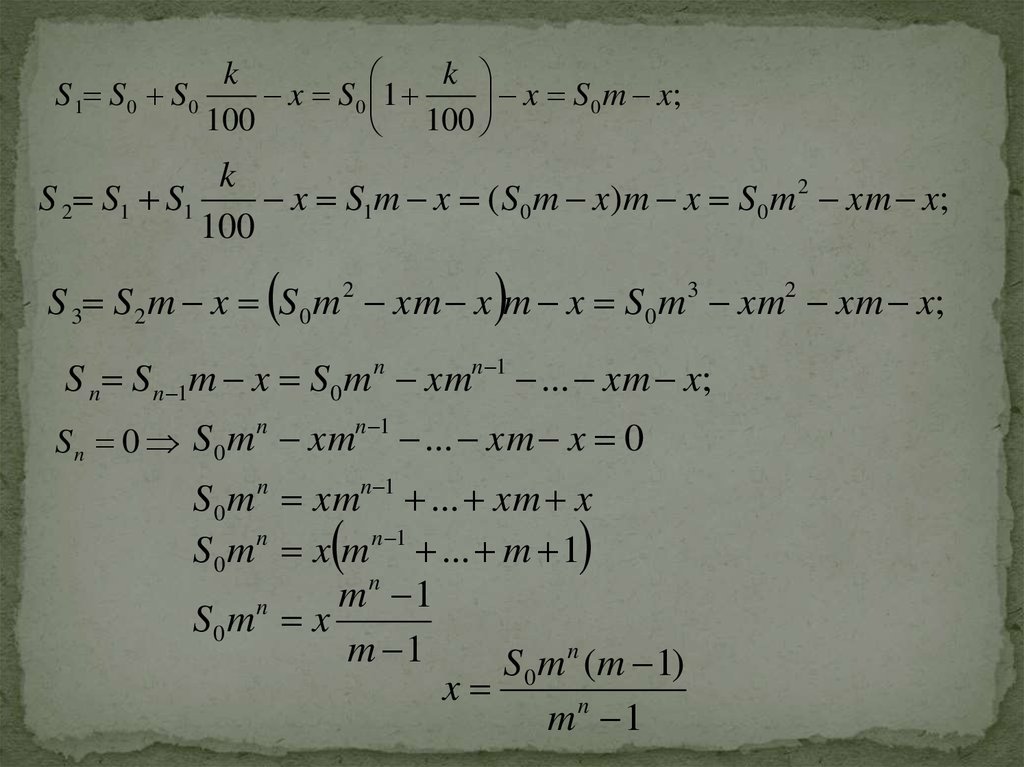



 Математика
Математика Экономика
Экономика








