Похожие презентации:
Средняя линия треугольника
1.
Классная работа.2. Задача.
• В равнобедренном треугольнике ABC с основанием ACчерез середину стороны AB проведена прямая DE,
параллельная AC. Известно, что AD=5 м, периметр
треугольника ABC равен 36 м, периметр треугольника DBE
равен 18 м.
• Найти AC, DE.
Дано:
ABC- р/б
AB=BC
DE || AC
AD=DB
AD=5 м
PABC 36 м
PDBE 18 м
Найти: AC, DE.
3. Средняя линия треугольника
4. Определение:
• Средней линией треугольниканазывается отрезок, соединяющий
середины двух сторон.
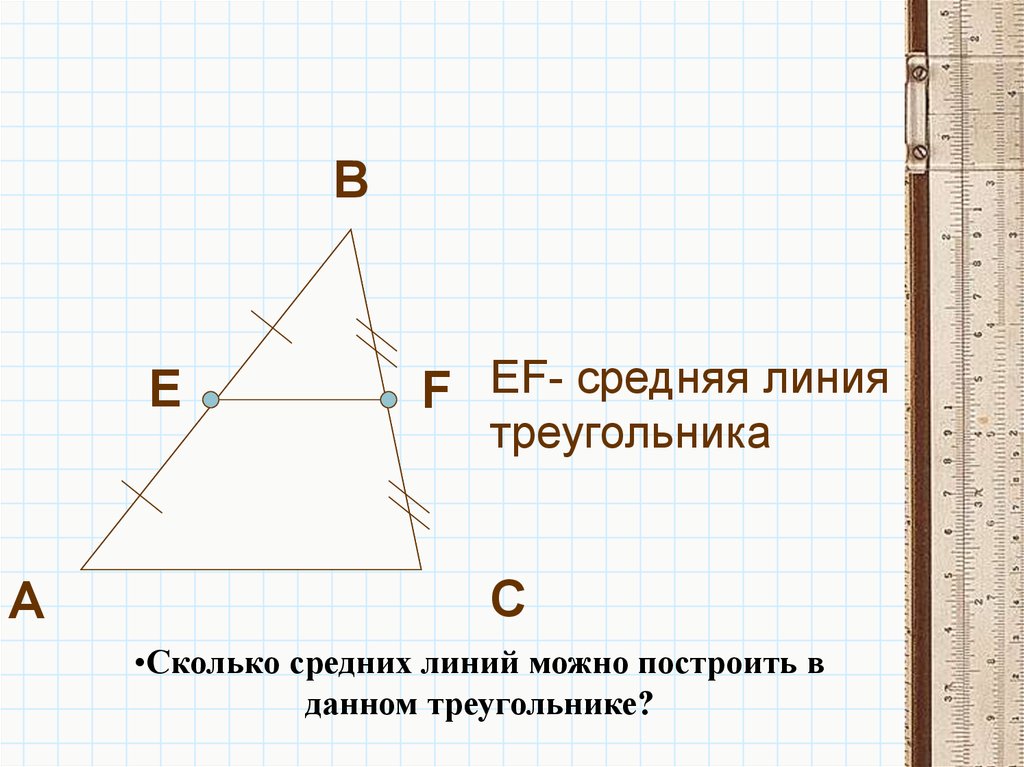
5.
BE
A
F EF- средняя линия
треугольника
C
•Сколько средних линий можно построить в
данном треугольнике?
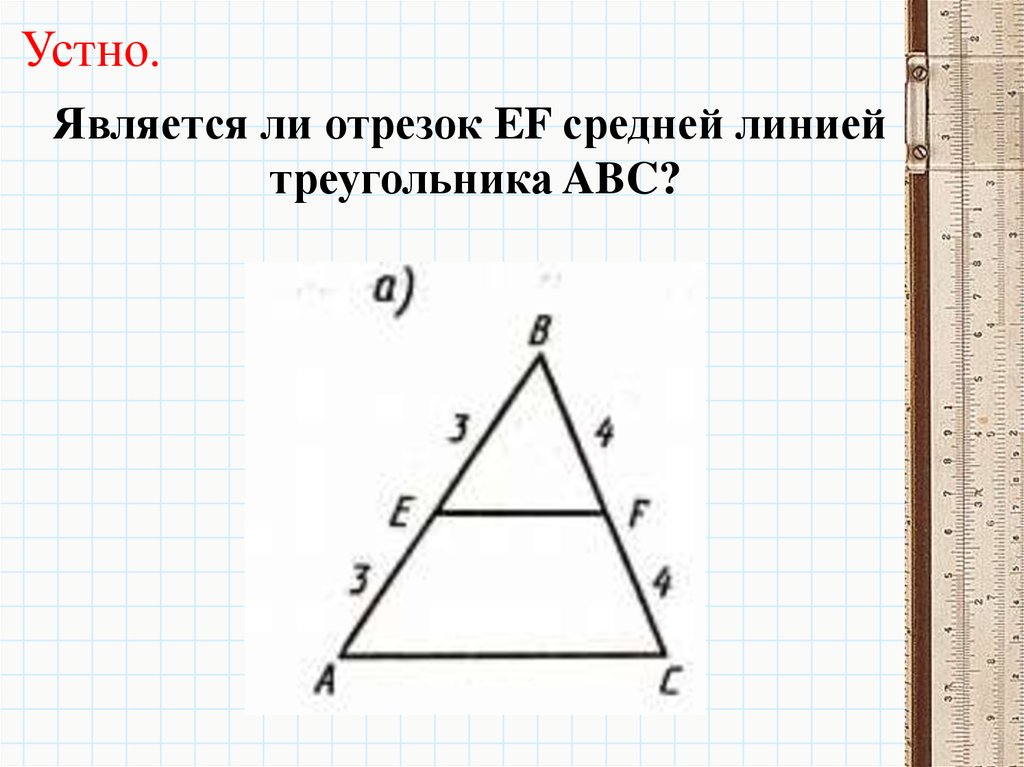
6.
Устно.Является ли отрезок EF средней линией
треугольника ABC?
7.
Устно.Является ли отрезок CD средней линией
треугольника MNK?
8. Теорема.
Средняя линия треугольника,соединяющая середины двух данных
сторон, параллельна третьей
стороне и равна ее половине.
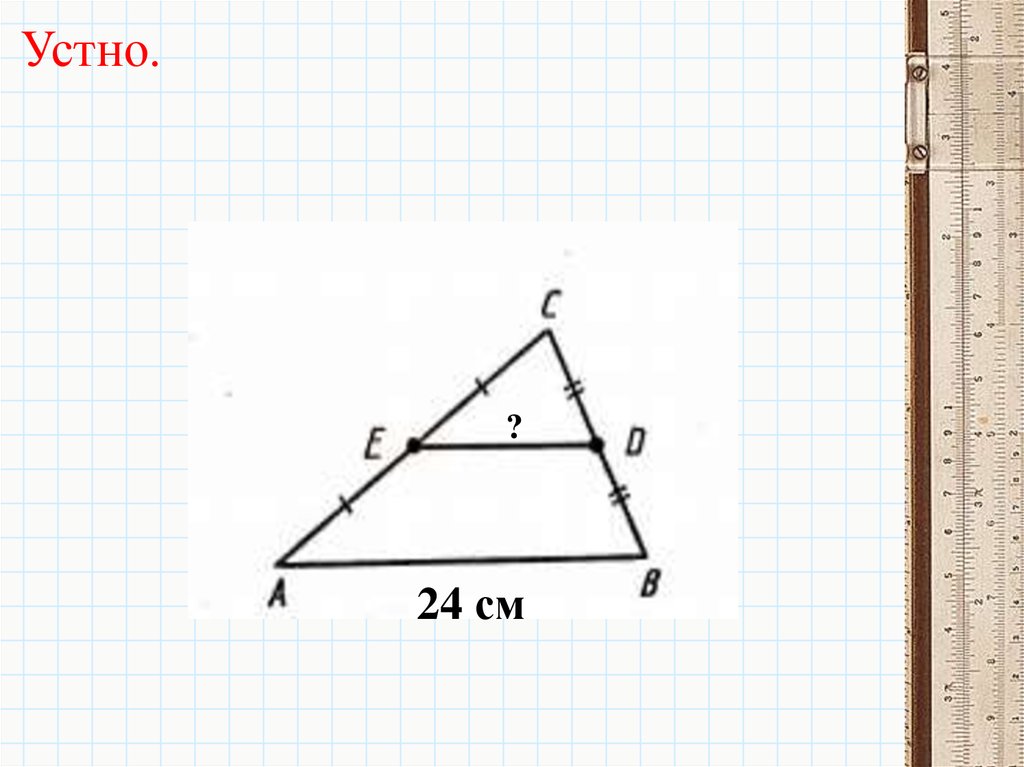
9.
Устно.?
24 см
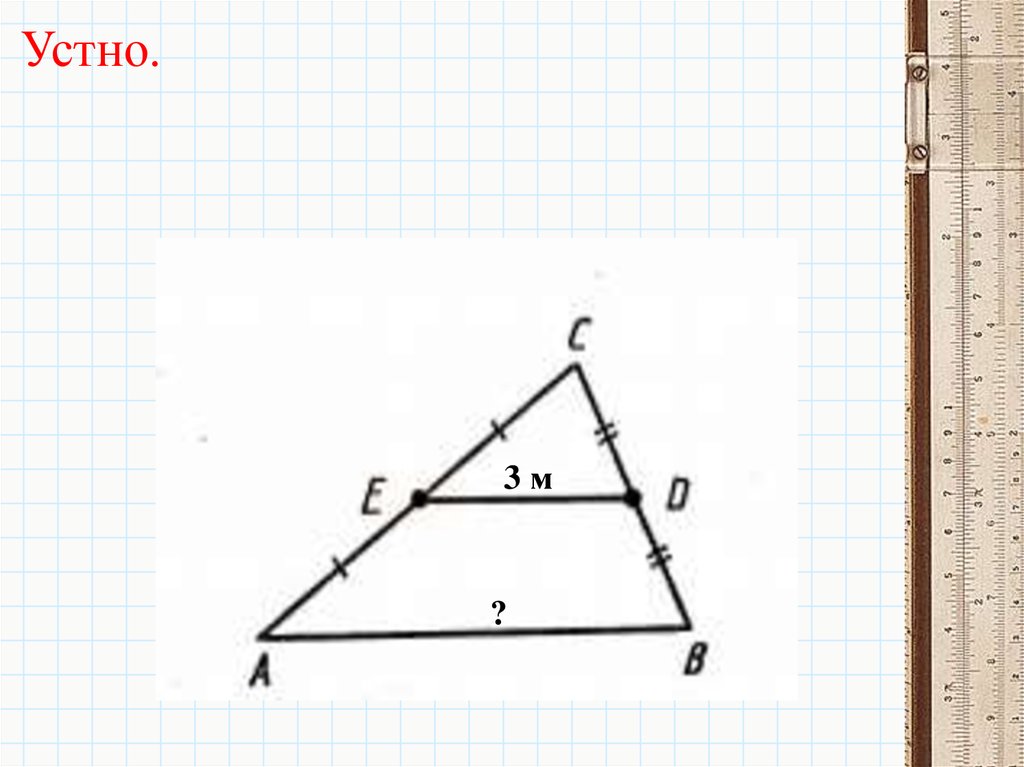
10.
Устно.3м
?






 Математика
Математика








