Похожие презентации:
Свойства функций (продолжение). 10 класс
1.
10 «Б» класс15.09.14
Коновальцева О.С.
2.
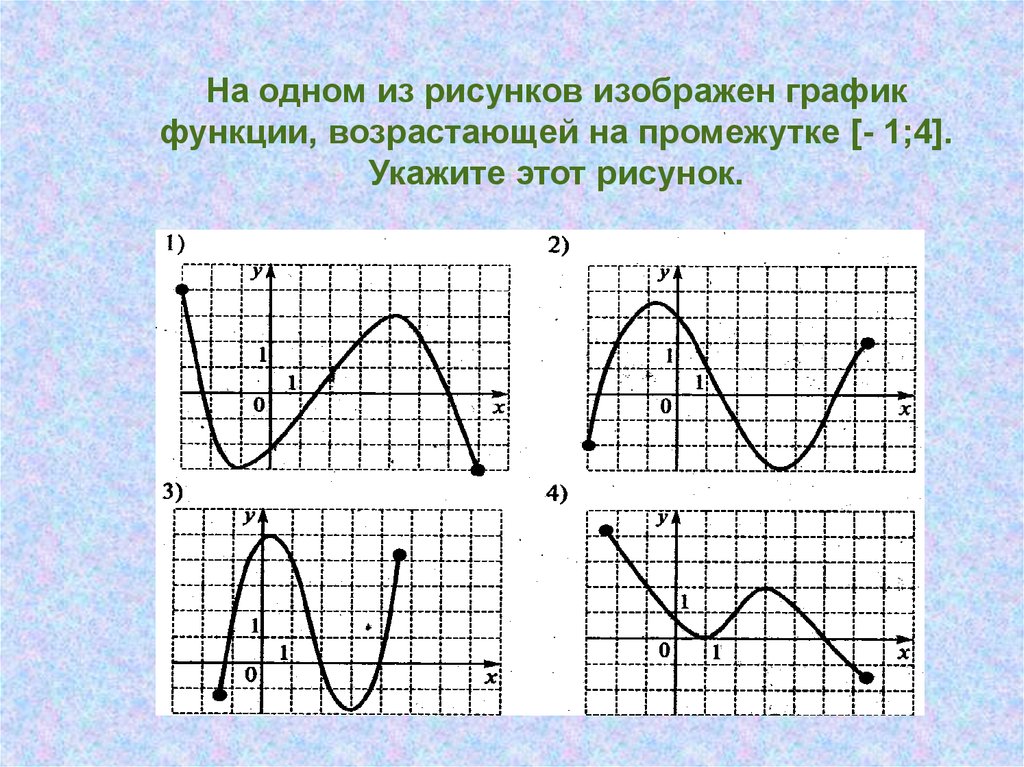
На одном из рисунков изображен графикфункции, возрастающей на промежутке [- 1;4].
Укажите этот рисунок.
3. На одном из рисунков изображен график функции, убывающей на промежутке [0 ; 3 ]. Укажите этот рисунок.
4.
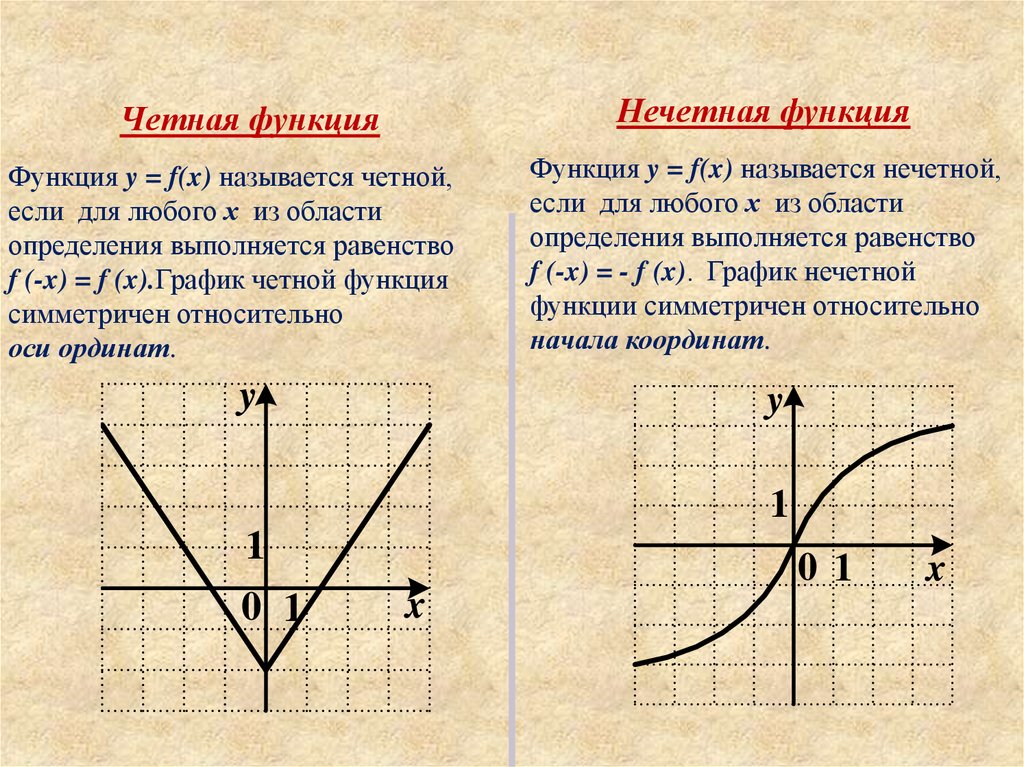
Нечетная функцияЧетная функция
Функция y = f(x) называется четной,
если для любого х из области
определения выполняется равенство
f (-x) = f (x).График четной функция
симметричен относительно
оси ординат.
y
Функция y = f(x) называется нечетной,
если для любого х из области
определения выполняется равенство
f (-x) = - f (x). График нечетной
функции симметричен относительно
начала координат.
y
1
1
0 1
0 1
x
x
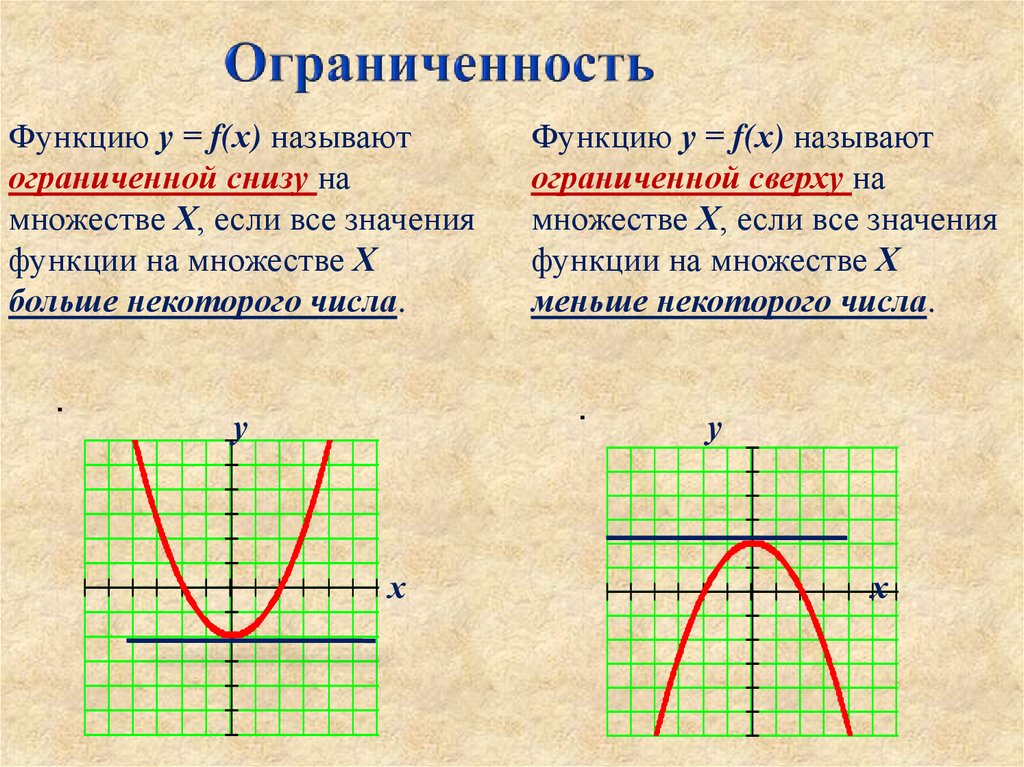
5. Ограниченность
Функцию у = f(х) называютограниченной снизу на
множестве Х, если все значения
функции на множестве Х
больше некоторого числа.
у
Функцию у = f(х) называют
ограниченной сверху на
множестве Х, если все значения
функции на множестве Х
меньше некоторого числа.
у
х
х
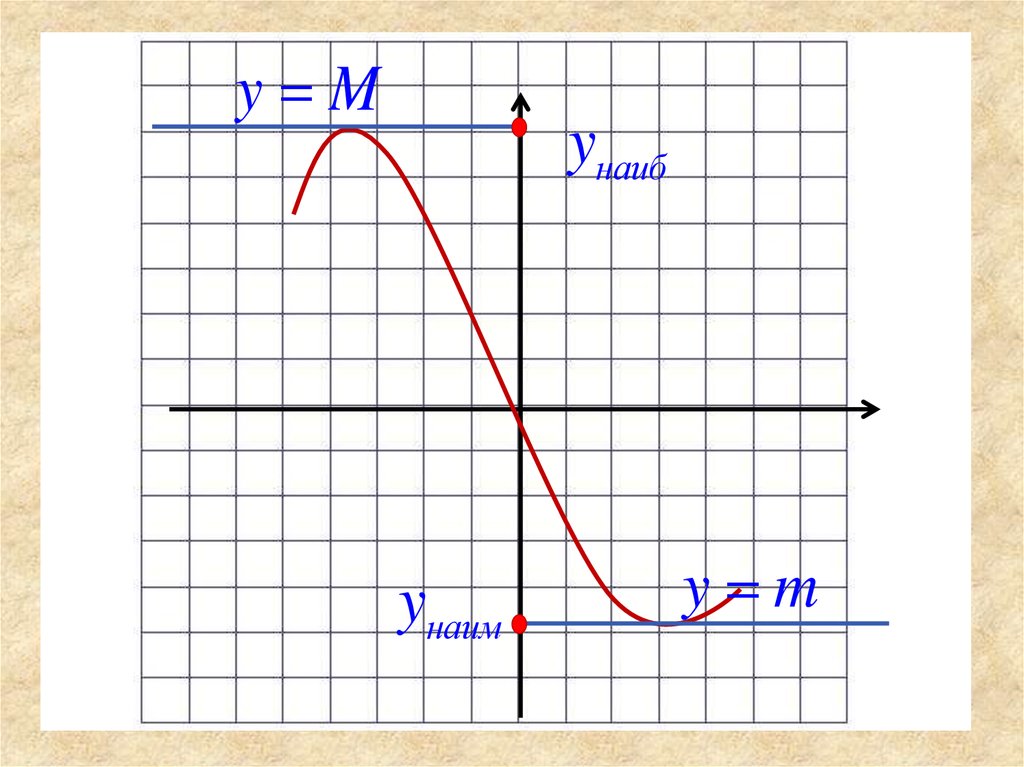
6. Наибольшее и наименьшее значения функции
Число m называют наименьшим значением функцииу = f(х) на множестве Х, если:
1) в области определения существует такая точка х0, что
f(х0) = m.
2) всех х из области определения выполняется неравенство
f(х) ≥ f(х0).
Число M называют наибольшим значением функции
у = f(х) на множестве Х, если:
1) в области определения существует такая точка х0, что
f(х0) = M.
2) для всех х из области определения выполняется
неравенство
f(х) ≤ f(х0).
7.
y Myнаиб
yнаим
y m
8.
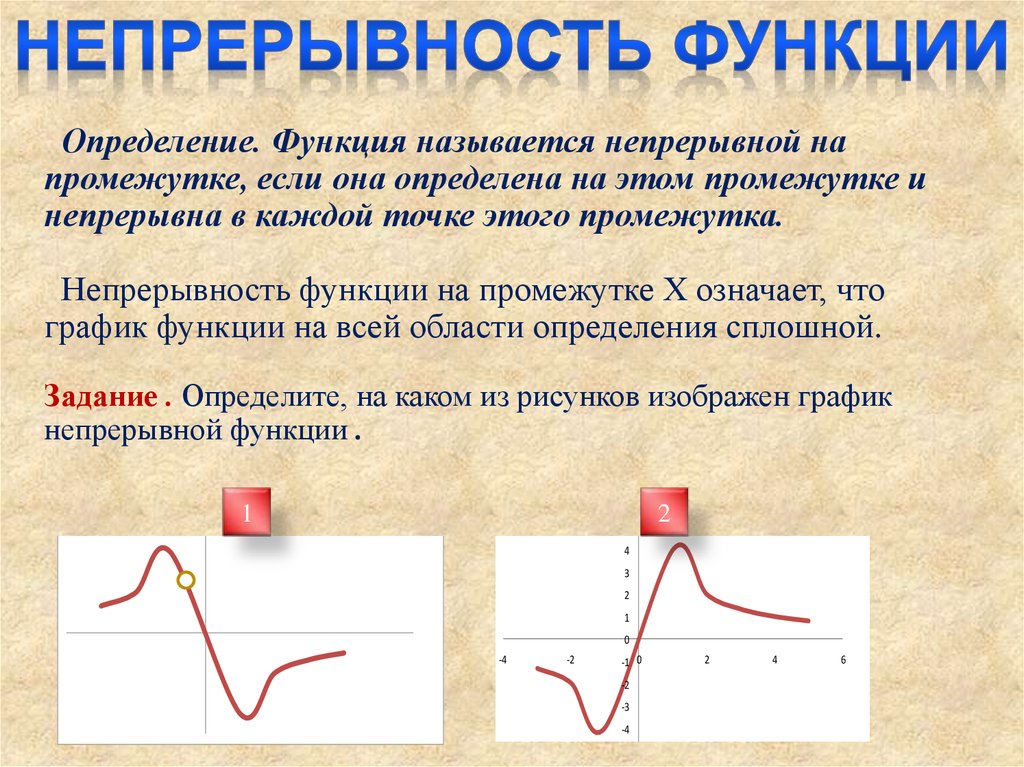
Определение. Функция называется непрерывной напромежутке, если она определена на этом промежутке и
непрерывна в каждой точке этого промежутка.
Непрерывность функции на промежутке Х означает, что
график функции на всей области определения сплошной.
Задание . Определите, на каком из рисунков изображен график
непрерывной функции .
1
5
2
4
3
2
1
0
-4
-2
-1 0
-2
-3
-4
-5
2
4
6
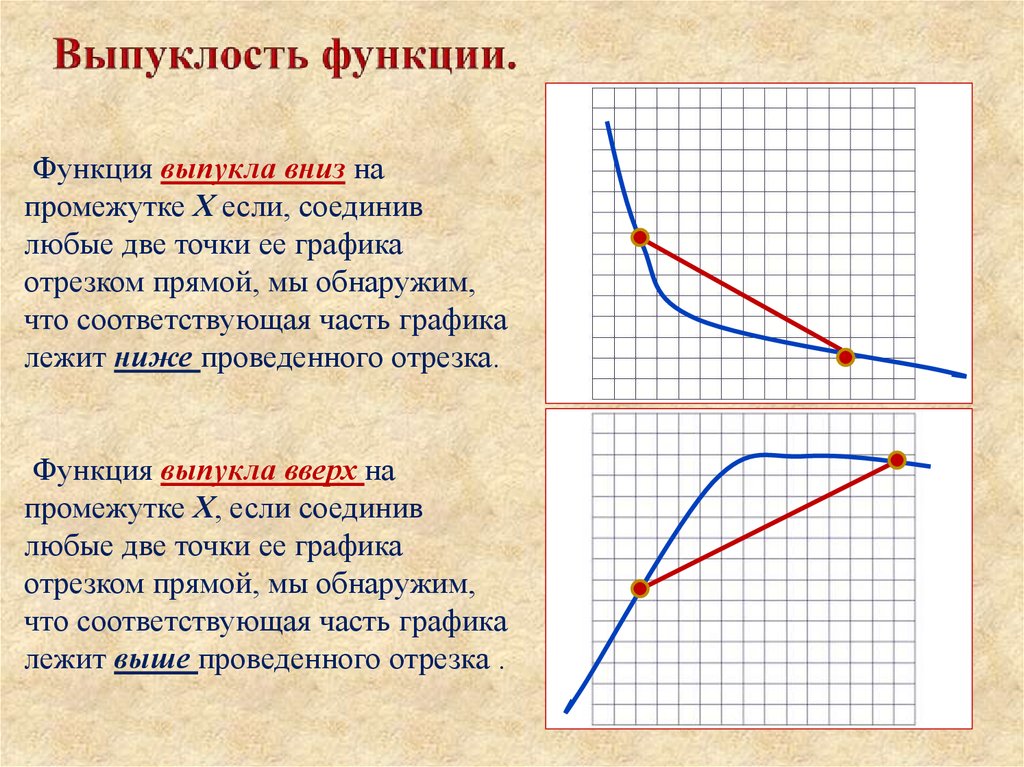
9. Выпуклость функции.
Функция выпукла вниз напромежутке Х если, соединив
любые две точки ее графика
отрезком прямой, мы обнаружим,
что соответствующая часть графика
лежит ниже проведенного отрезка.
Функция выпукла вверх на
промежутке Х, если соединив
любые две точки ее графика
отрезком прямой, мы обнаружим,
что соответствующая часть графика
лежит выше проведенного отрезка .
10. План исследования функции
1.Область определения2.Монотонность
3.Ограниченность
4.Наибольшее, наименьшее значение
5.Непрерывность
6.Область значения
7.Выпуклость
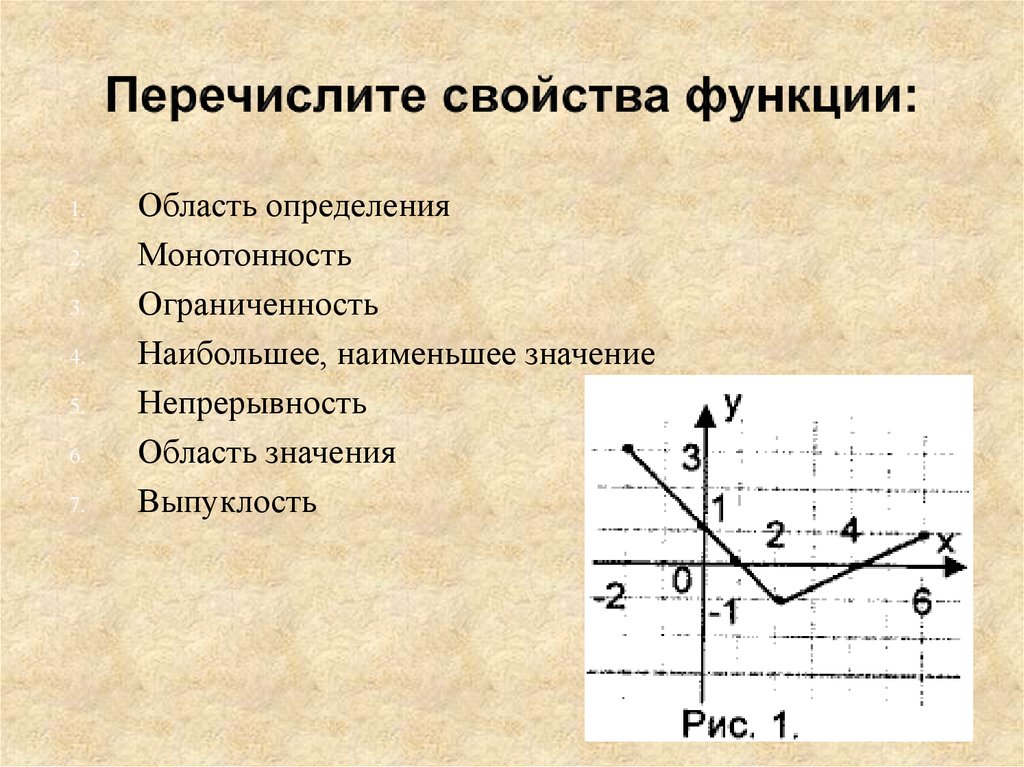
11. Перечислите свойства функции:
1.2.
3.
4.
5.
6.
7.
Область определения
Монотонность
Ограниченность
Наибольшее, наименьшее значение
Непрерывность
Область значения
Выпуклость
12.
Учебник:стр.11-18(выучить все определения)
№
2.12; 2.14.

![На одном из рисунков изображен график функции, убывающей на промежутке [0 ; 3 ]. Укажите этот рисунок. На одном из рисунков изображен график функции, убывающей на промежутке [0 ; 3 ]. Укажите этот рисунок.](https://cf2.ppt-online.org/files2/slide/b/bHT19VgzPwCrEtZ2AN4vdR63cSDQfsmXeInh5qx8a/slide-2.jpg)



 Математика
Математика








