Свойства функции. 10 класс

1.

Свойства функции
АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО
АНАЛИЗА
10КЛАСС

2.

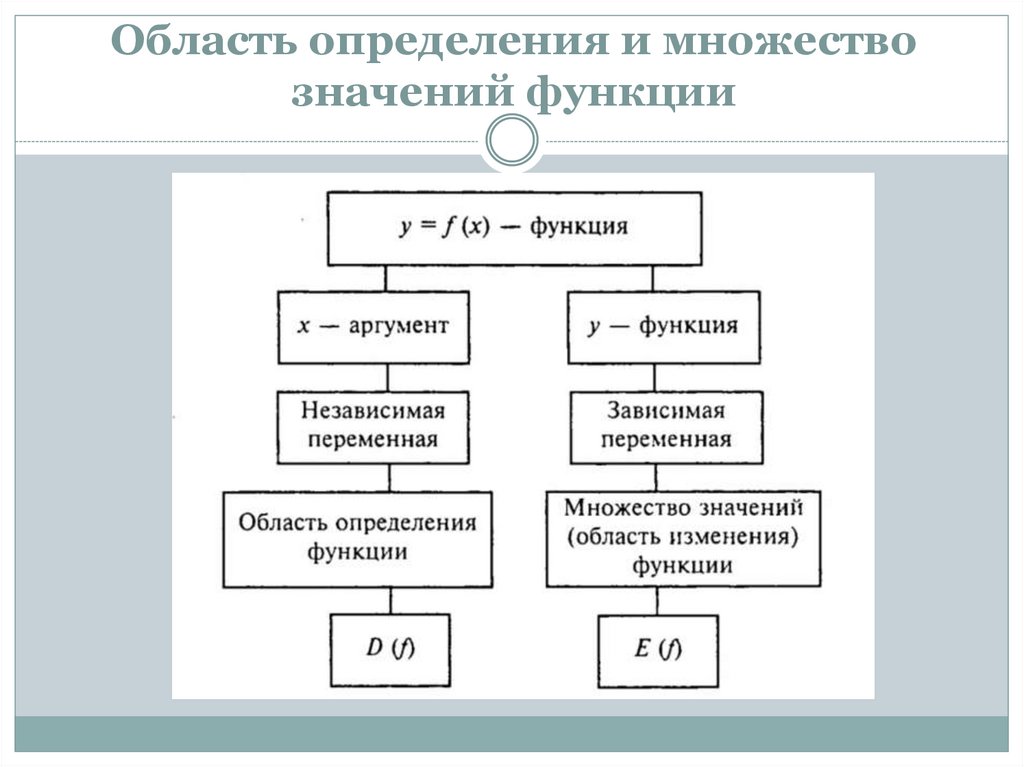
Область определения и множество
значений функции

3.

Композиция функций
Сложная функция (функция от функции) y=f(g(x))
называется композицией функций f и g, где g(x) –
внутренняя функция, f(t) – внешняя функция.
НАПРИМЕР
Пусть g(x)=2х+1, f(х) = х², тогда композицией (сложной
функцией) функций f и g является y= (2х+1)²=f(2х+1)

4.

Композиция функций
№
Композиция
п/п
функций
1
y=(4-3x)³
2
3
4
5
y=(x³+1)²
y=(x²)³+1
f(x²-2)=√x²-2
Внешняя
функция
f= x³
Внутренняя
функция
g=4-3x
f=1/x
g=x²+1
f=x²
f=x³+1
f=√x
g=x³+1
g=x²
g=x²-2
Заполните таблицу

5.

Свойства функции
Свойство функции
Схема
исследования
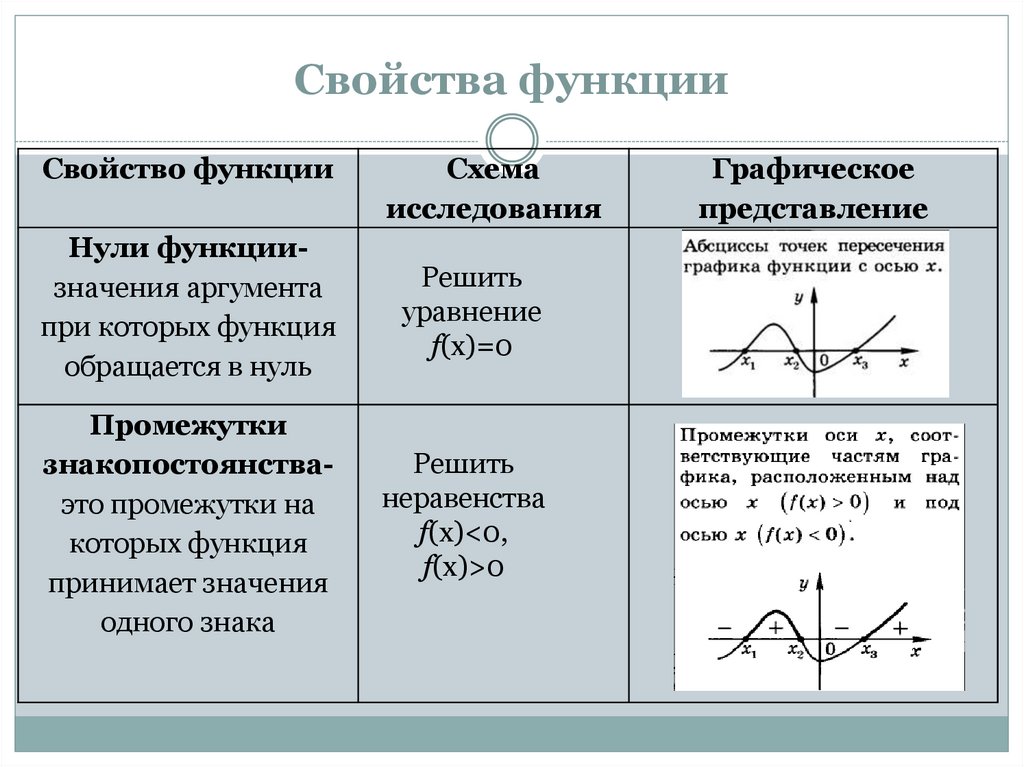
Нули функциизначения аргумента
при которых функция
обращается в нуль
Решить
уравнение
f(x)=0
Промежутки
знакопостоянстваэто промежутки на
которых функция
принимает значения
одного знака
Решить
неравенства
f(x)<0,
f(x)>0
Графическое
представление

6.

Свойства функции

7.

Свойства функции
Свойство
функции
Схема исследования
Графическое
представление
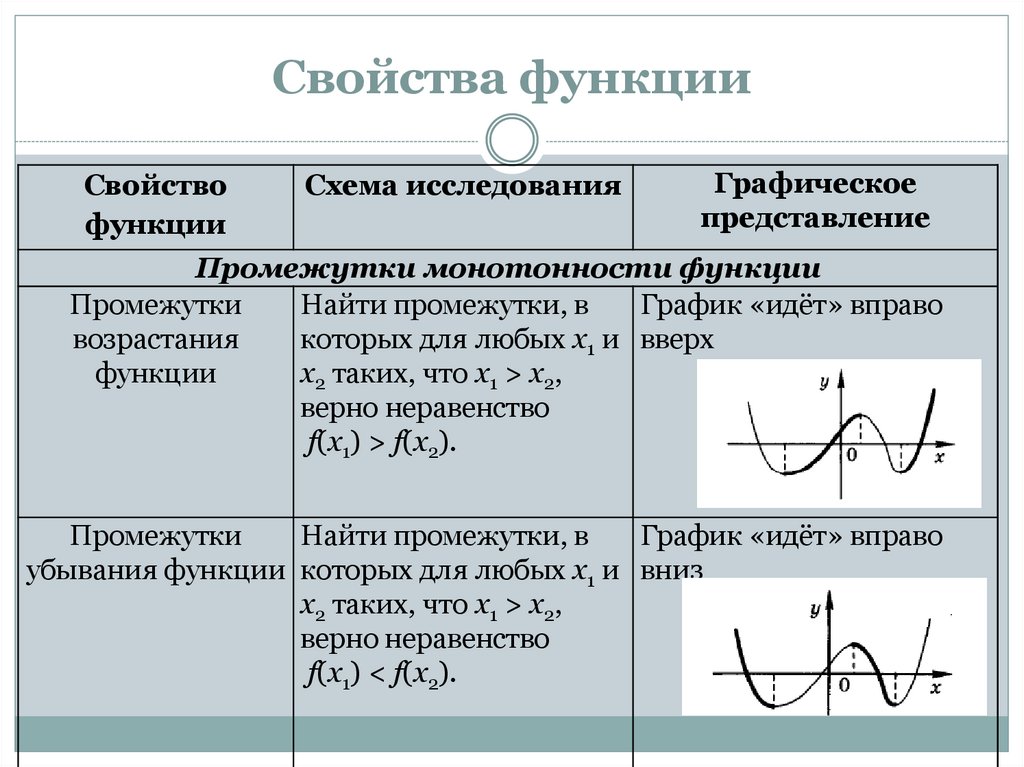
Промежутки монотонности функции
Промежутки
Найти промежутки, в
График «идёт» вправо
возрастания
которых для любых х1 и вверх
функции
х2 таких, что х1 > х2,
верно неравенство
f(х1) > f(х2).
Промежутки
Найти промежутки, в
График «идёт» вправо
убывания функции которых для любых х1 и вниз
х2 таких, что х1 > х2,
верно неравенство
f(х1) < f(х2).

8.

Свойства функции

9.

Свойства функции
Графическое
представление
Свойство
функции
Схема исследования
Четность
функции
1. D(f) симметрична
относительно 0.
2. Для любого х D(f)
выполняется
равенство
f(-х) = f(х).
График симметричен
относительно
оси ординат
Нечетность
функции
1. D(f) симметрична
относительно 0.
2. Для любого х D(f)
выполняется
f(-х) = - f(х).
График симметричен
относительно
начала
координат

10.

Свойства функции
Свойство
функции
Схема исследования
Периодичность
функции
Для любого х D(f) и
Т≠0 выполняется
равенство
f(x – T) = f(x) = f(x + T).
Графическое
представление

11.

Свойства функции
Свойство
функции
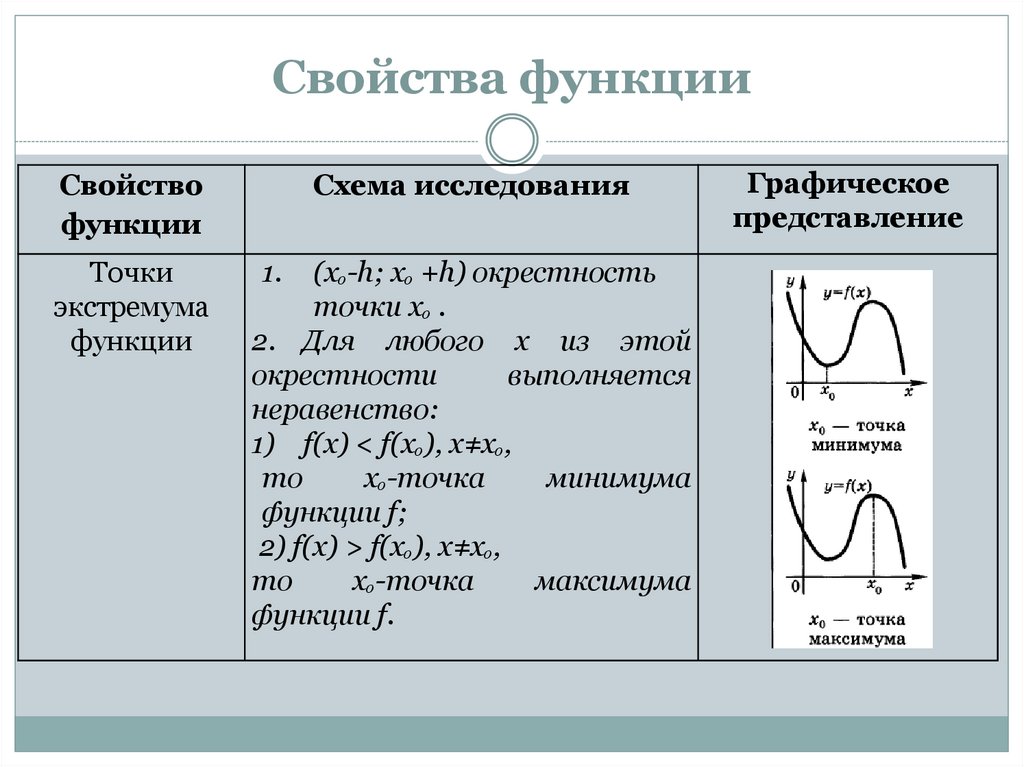
Точки
экстремума
функции
Схема исследования
1.
(хₒ-h; хₒ +h) окрестность
точки хₒ .
2. Для любого х из этой
окрестности
выполняется
неравенство:
1) f(x) < f(xₒ), х≠хₒ,
то
хₒ-точка
минимума
функции f;
2) f(x) > f(xₒ), х≠хₒ,
то
хₒ-точка
максимума
функции f.
Графическое
представление

12.

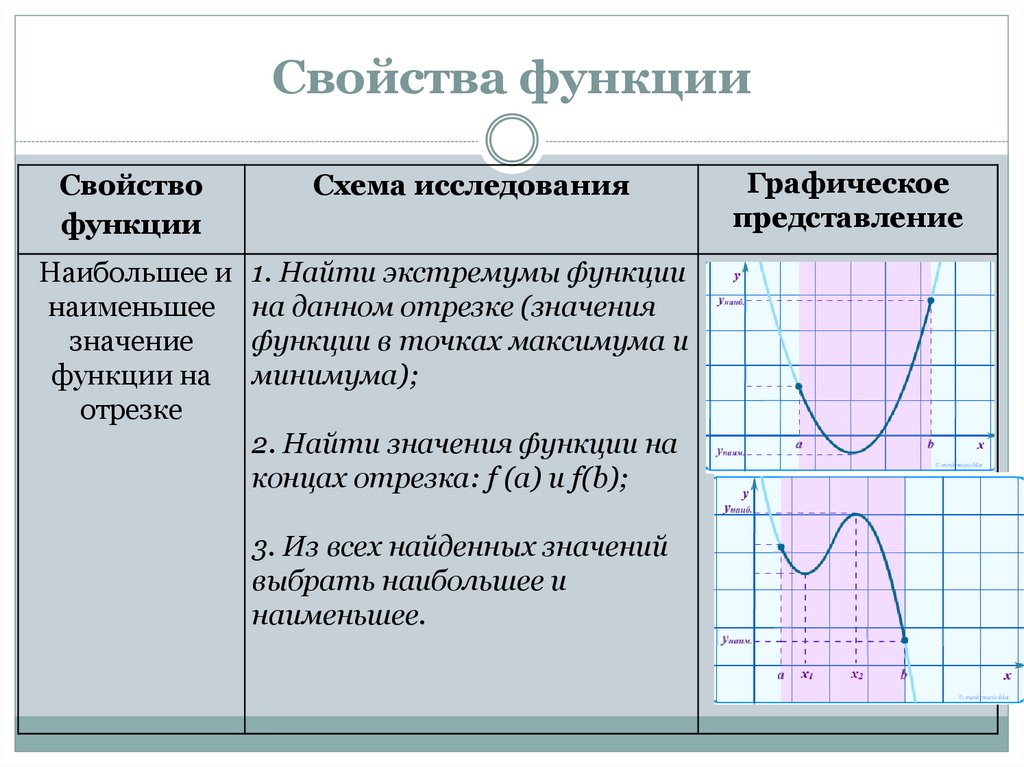
Свойства функции
Свойство
функции
Схема исследования
Наибольшее и 1. Найти экстремумы функции
наименьшее на данном отрезке (значения
значение
функции в точках максимума и
функции на минимума);
отрезке
2. Найти значения функции на
концах отрезка: f (a) и f(b);
3. Из всех найденных значений
выбрать наибольшее и
наименьшее.
Графическое
представление

13.

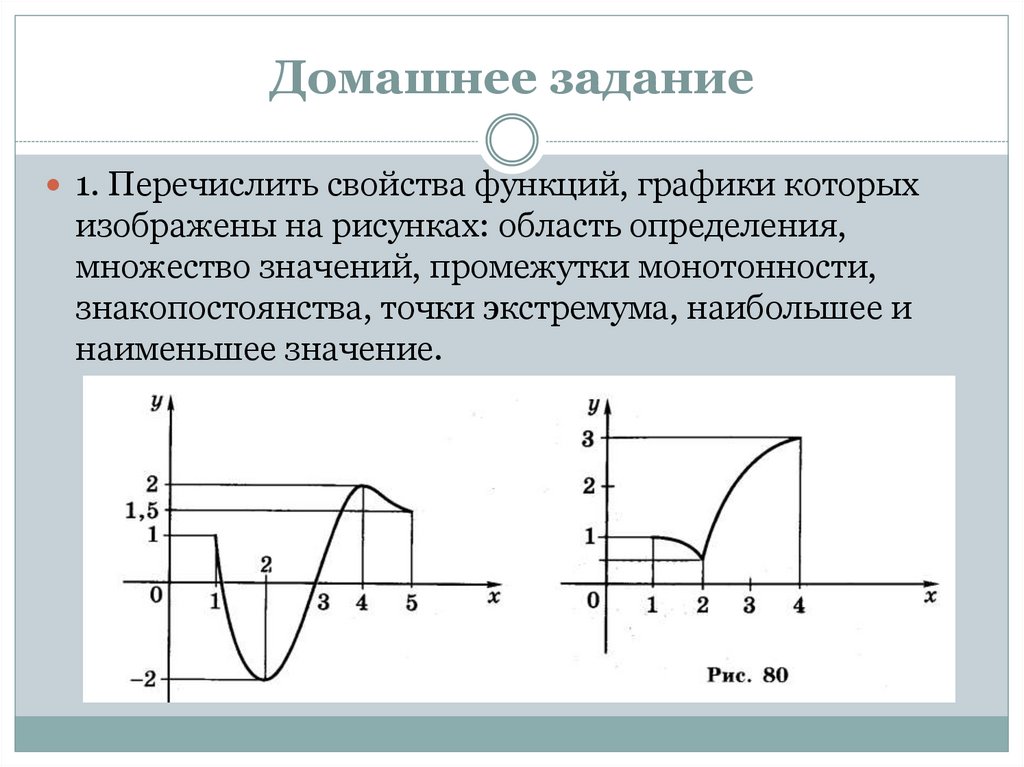
Домашнее задание
1. Перечислить свойства функций, графики которых
изображены на рисунках: область определения,
множество значений, промежутки монотонности,
знакопостоянства, точки экстремума, наибольшее и
наименьшее значение.

14.

Домашнее задание
2. Функция y = f(x) определена на всей числовой прямой.
На рисунке изображен график этой функции при 0 ≤ x ≤ 4.
а) Найдите f(−3), если y = f(x) является четной и постройте
график этой функции на отрезке -4 ≤ x ≤ 4;
б) Постройте график y = f(x) на отрезке -4 ≤ x ≤ 4, если она
является нечетной;
в)* Постройте график y = f(x) на отрезке -8 ≤ x ≤ 4, если она
является периодической с периодом Т=4