Похожие презентации:
Числовые функции. 10 класс
1. Числовые функции
2. Свойства функции
• Чётность нечетность• Периодичность
• Нули функции
• Монотонность
• Экстремумы
• Асимптоты
3. Четная и нечетная функция
Функция называетсячетной если:
•область определения
функции симметрична
относительно нуля
•для любого x из области
определения
f(-x) = f(x)
2n,
y=x
n Z;
y = cos x .
Функция называется нечетной если:
• область определения функции
симметрична относительно нуля
• для любого x из области
определения
f(-x) = -f(x)
y = x 2n + 1, n
y = sin x .
Z;
4.
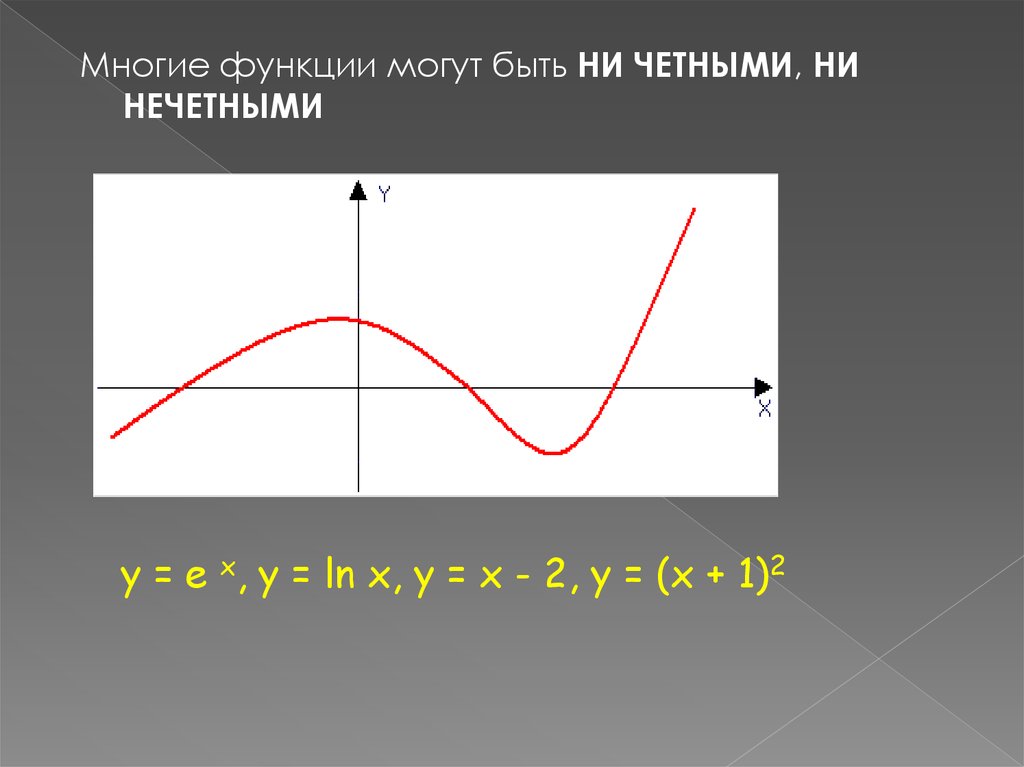
Многие функции могут быть НИ ЧЕТНЫМИ, НИНЕЧЕТНЫМИ
y = e x, y = ln x, y = x - 2, y = (x + 1)2
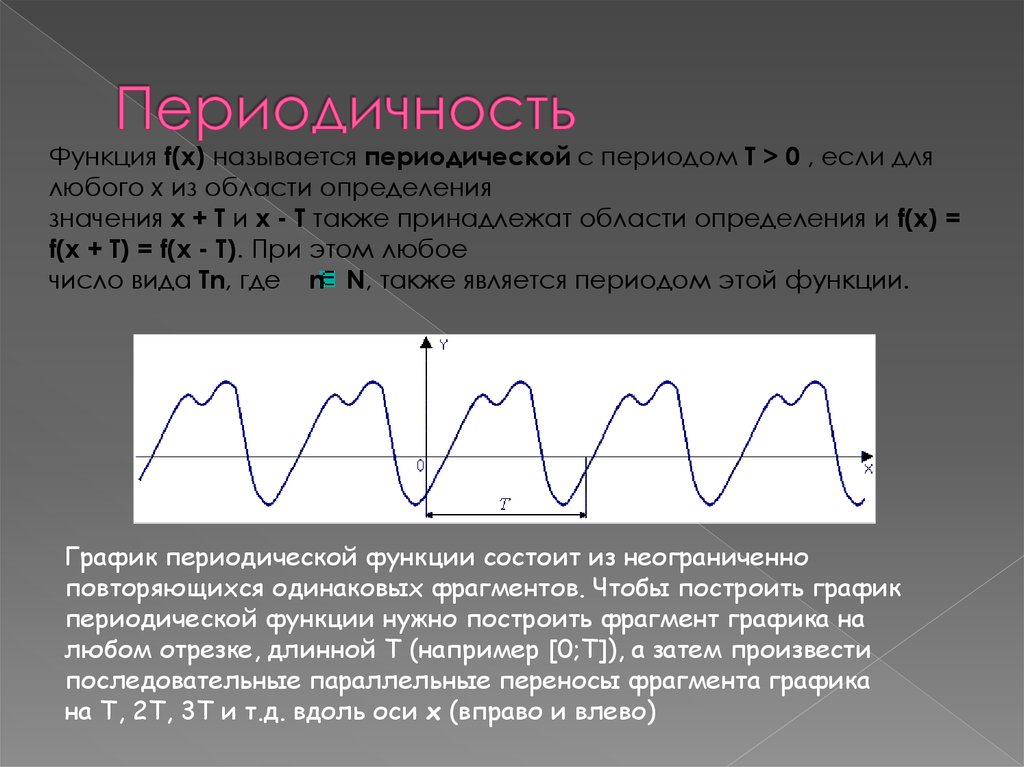
5. Периодичность
Функция f(x) называется периодической с периодом T > 0 , если длялюбого x из области определения
значения x + T и x - T также принадлежат области определения и f(x) =
f(x + T) = f(x - T). При этом любое
число вида Tn, где n N, также является периодом этой функции.
График периодической функции состоит из неограниченно
повторяющихся одинаковых фрагментов. Чтобы построить график
периодической функции нужно построить фрагмент графика на
любом отрезке, длинной T (например [0;T]), а затем произвести
последовательные параллельные переносы фрагмента графика
на T, 2T, 3T и т.д. вдоль оси x (вправо и влево)
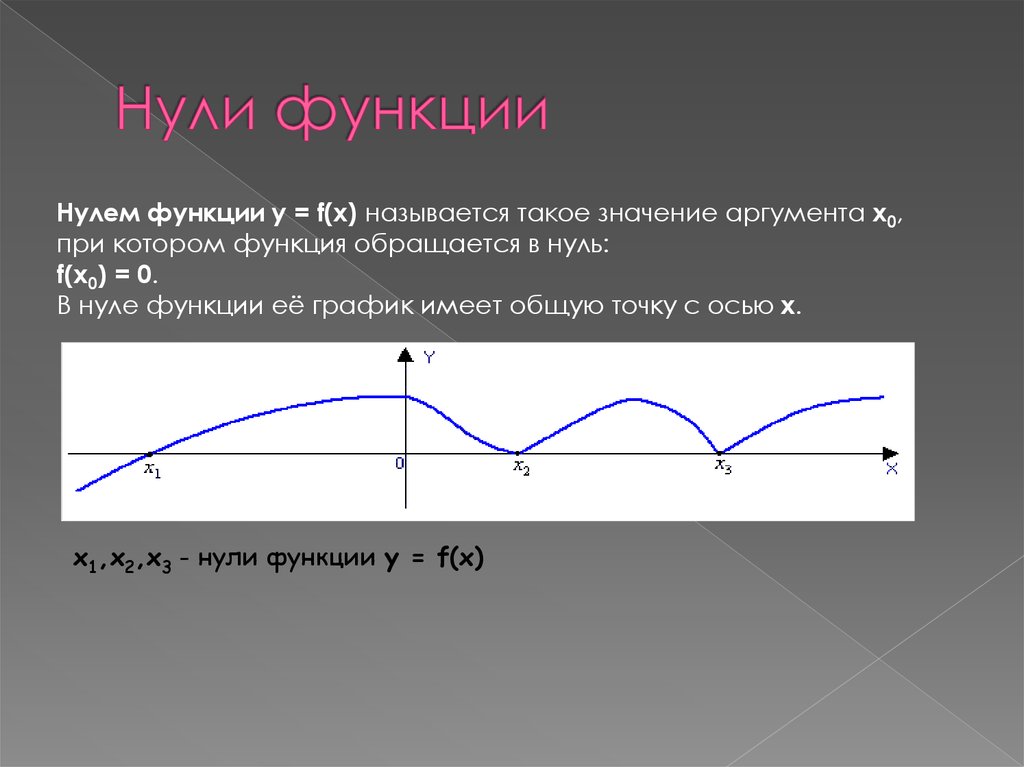
6. Нули функции
Нулем функции y = f(x) называется такое значение аргумента x0,при котором функция обращается в нуль:
f(x0) = 0.
В нуле функции её график имеет общую точку с осью x.
x1,x2,x3 - нули функции y = f(x)
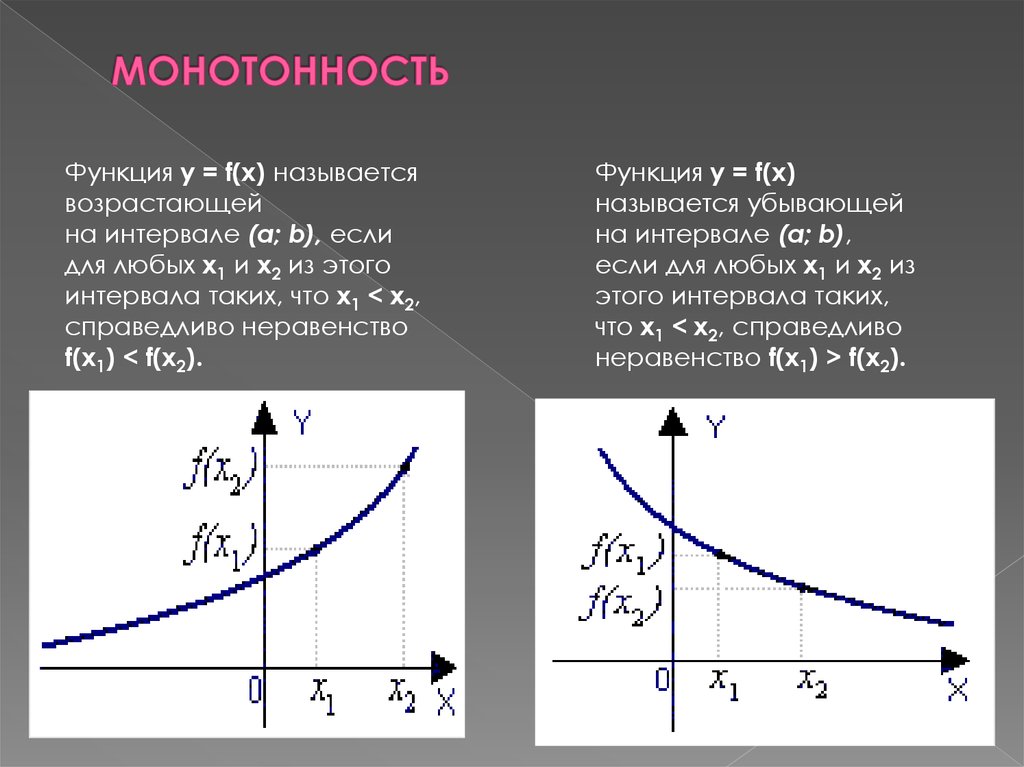
7. МОНОТОННОСТЬ
Функция y = f(x) называетсявозрастающей
на интервале (a; b), если
для любых x1 и x2 из этого
интервала таких, что x1 < x2,
справедливо неравенство
f(x1) < f(x2).
Функция y = f(x)
называется убывающей
на интервале (a; b),
если для любых x1 и x2 из
этого интервала таких,
что x1 < x2, справедливо
неравенство f(x1) > f(x2).
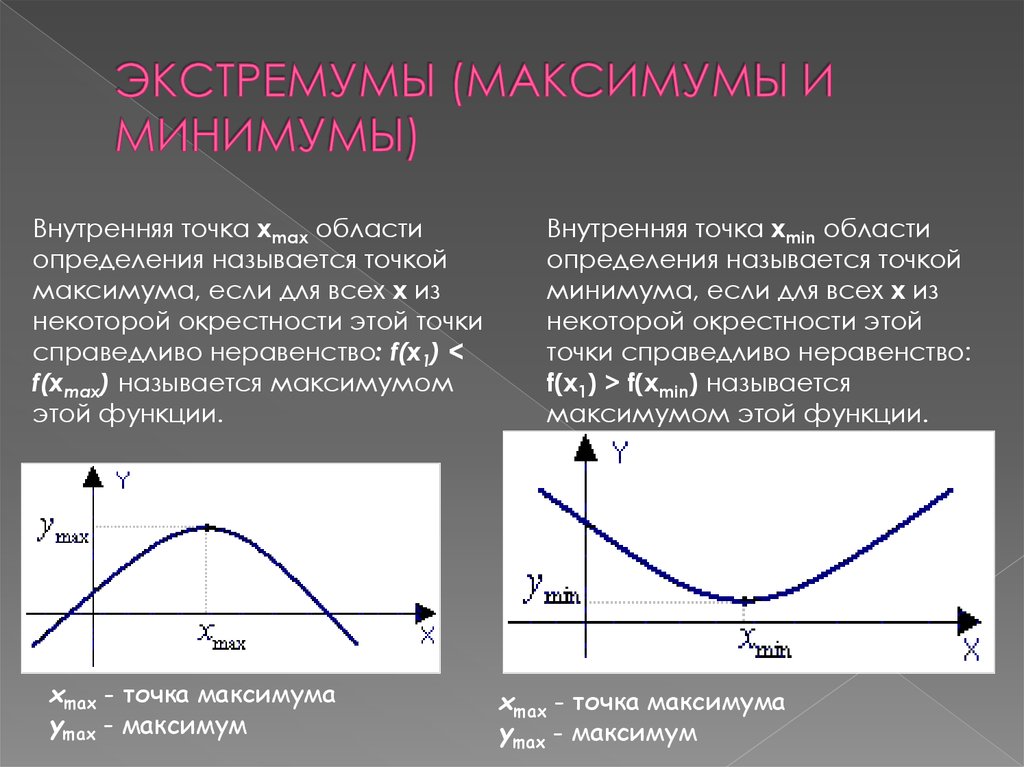
8. ЭКСТРЕМУМЫ (МАКСИМУМЫ И МИНИМУМЫ)
Внутренняя точка xmax областиопределения называется точкой
максимума, если для всех x из
некоторой окрестности этой точки
справедливо неравенство: f(x1) <
f(xmax) называется максимумом
этой функции.
xmax - точка максимума
ymax - максимум
Внутренняя точка xmin области
определения называется точкой
минимума, если для всех x из
некоторой окрестности этой
точки справедливо неравенство:
f(x1) > f(xmin) называется
максимумом этой функции.
xmax - точка максимума
ymax - максимум
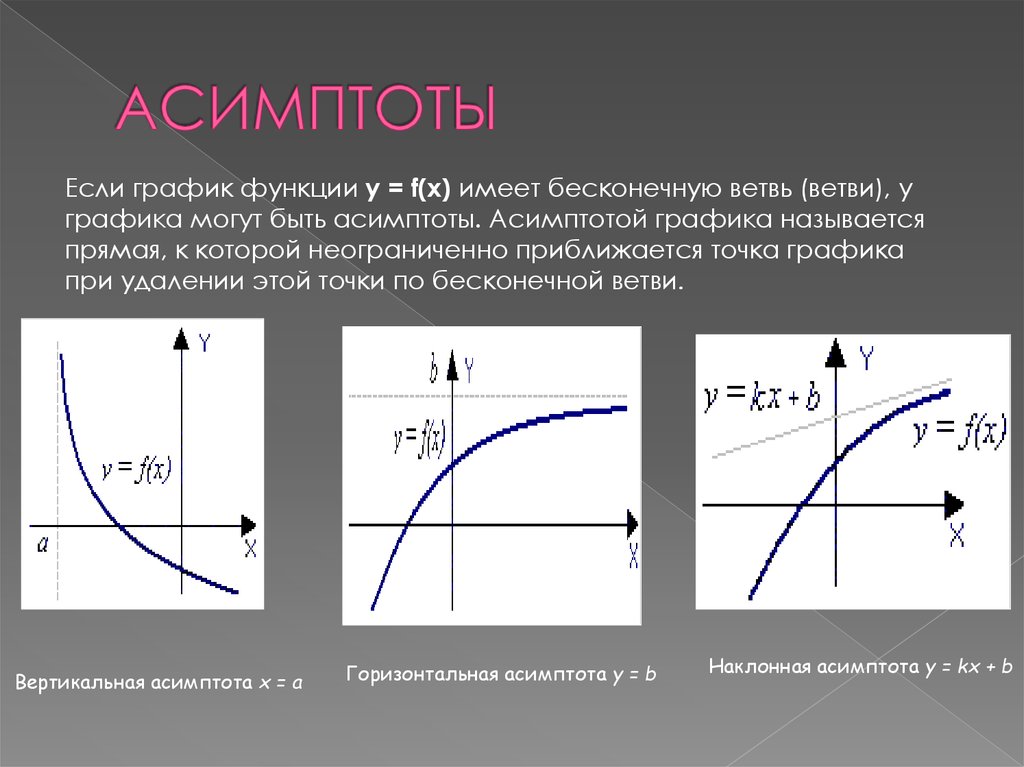
9. АСИМПТОТЫ
Если график функции y = f(x) имеет бесконечную ветвь (ветви), уграфика могут быть асимптоты. Асимптотой графика называется
прямая, к которой неограниченно приближается точка графика
при удалении этой точки по бесконечной ветви.
Вертикальная асимптота x = a
Горизонтальная асимптота y = b
Наклонная асимптота y = kx + b
10. Обратная функция
Понятие обратной функции применимо к функциям, обладающимследующим свойством: каждому значению y из области определения
соответствует единственное значение x из области определения этой
функции. Для многих функций это свойство выполняется лишь на части
области определения, в частности (для функции y = x2 таким
промежутком является, например, луч [0;
, для функции y =sin x отрезок [- 2; 2]).
Функция g называется обратной для функции f, если каждому y из
области значений функции f функция g ставит в соответствие такое x из
области определения функции f, что y = f(x). Таким образом, если y =
f(x), то x = g(y).
Функции f и g являются взаимно обратными.
• Область определения функции f является областью значений функции
g, а область значений
функции f является областью определения функции g.
• Графики взаимно обратных функций симметричны друг другу
относительно прямой y = x
)
/
/
11. НАХОЖДЕНИЕ ФОРМУЛЫ ДЛЯ ФУНКЦИИ, ОБРАТНОЙ ДАННОЙ
Пользуясь формулой y =f(x), следует выразить x
через y, а в полученной
формуле x = g(y)
заменить x на y, а y на x.
Пример:
Найти формулу для функции, обратной функции:
Выразить x через y: x = 2y - 2.
Заменить x на y: y = 2x - 2.
Результат: функция y = 2x - 2 является обратной для функции .
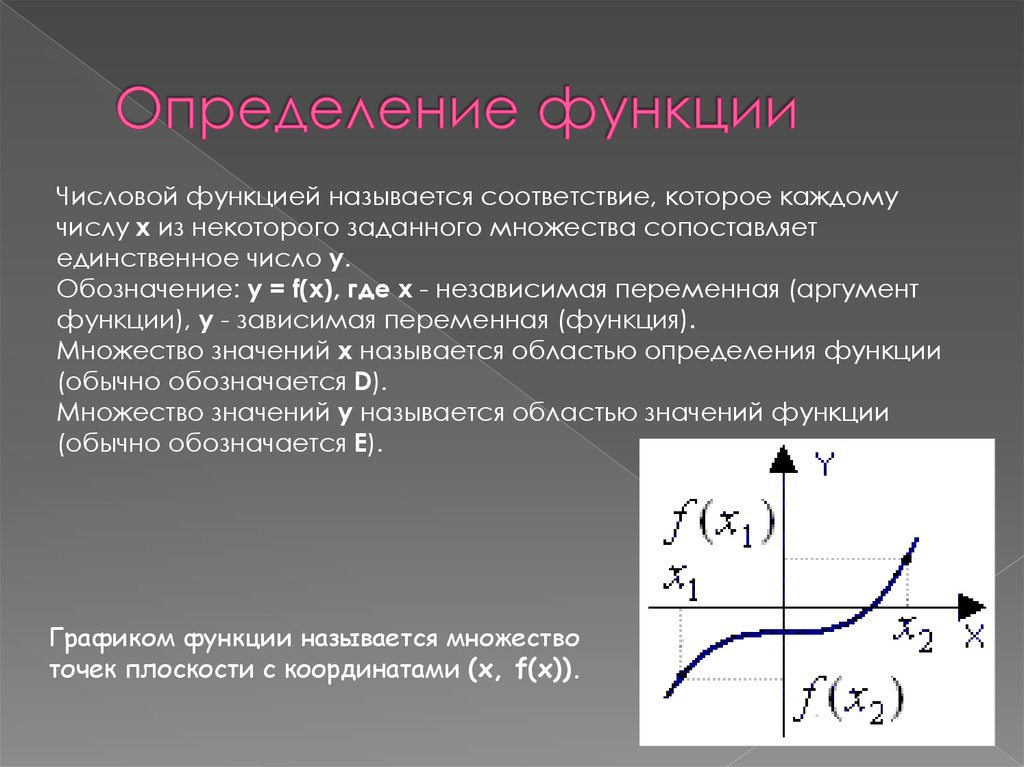
12. Определение функции
Числовой функцией называется соответствие, которое каждомучислу x из некоторого заданного множества сопоставляет
единственное число y.
Обозначение: y = f(x), где x - независимая переменная (аргумент
функции), y - зависимая переменная (функция).
Множество значений x называется областью определения функции
(обычно обозначается D).
Множество значений y называется областью значений функции
(обычно обозначается E).
Графиком функции называется множество
точек плоскости с координатами (x, f(x)).
13. СПОСОБЫ ЗАДАНИЯ ФУНКЦИЙ
• Аналитический способ: функция задается с помощьюматематической формулы ( y = x 2, y = ln x) в которой зависимая
переменная выражается через независимую.
Формула указывает те действия и их последовательность, которые
нужно совершить над независимой переменной,
x
1
2
3 4
5
y
2
4
6 8
1
0
•чтобы вычислить значение функции при заданном значении
аргумента.
• Табличный способ: функция задается с помощью таблицы:
14.
•Графический способ: функция задается с помощьюграфика.
Графики некоторых функций имеют свои названия:
• Параболой называется график квадратичной функции
• Описательный способ: функция задается словесным
описанием.
• Кубической параболой называется график функции y = x
3
• Гиперболой называется график обратной пропорциональности
(y = k/x )
15. Периодическая функция
Функция f(z) от одного переменного z называется периодической, еслиможно найти такое число а, чтобы имело место равенство f(z+a) = f(z)
для всяких значений переменного z, действительных, мнимых и
комплексных. Число а будет периодом функции. П. функции от одного
переменного могут быть лишь однопериодичные либо
двупериодичные. Если все возможные периоды суть положительно
или отрицательно взятые кратные одного первоначального периода
2ω, то функция однопериодична. Таковы функции еZ, sinz,
первоначальные периоды которых суть: первой 2πi, второй 2π, где
i = √(—1). Все возможные периоды двупериодической функции могут
быть составлены через кратное сложение или вычитание двух разных
первоначальных периодов 2ω1 и 2ω2, отношение которых есть
величина мнимая. Примерами таких функций служат функции
эллиптические.









 Математика
Математика








