Похожие презентации:
Решение неравенств, содержащих переменную под знаком модуля
1. Решение неравенств, содержащих переменную под знаком модуля.
2.
Необходимые умения.Уметь решать рациональные неравенства методом
интервалов.
http://tashah.ucoz.ru/load/egeh/egeh_s3/s3_1_reshenie_racionalnykh_neravenstv_metodom_inter
valov/15-1-0-85
Понимать значение понятий: система, совокупность.
Уметь решать системы и совокупности.
http://ta-shah.ucoz.ru/load/egeh/egeh_s3/s3_2_sistemy_i_sovokupnosti/15-1-0-86
16.07.2019
2
3.
Методы решения.Универсальный способ (по определению модуля)
Метод интервалов (обобщение метода по определению)
Использование альтернативных схем
Использование свойств модулей
Метод рационализации (замены множителей)
16.07.2019
3
4.
Универсальный способ (по определению модуля)а , если а 0
a
а , если а 0
Пример 1. 3 x 7 6
1 случай.
3 x 7 0
3 x 7 6
7
x
3
x 13
3
7
3
Решением неравенства
является объединение
16.07.2019
решений всех случаев.
=> если под знаком модуля находится
функция от х, которая может принимать
как отрицательные, так и неотрицательные
значения, то необходимо рассмотреть два
варианта раскрытия для каждого из модулей.
2 случай.
13
3
3 x 7 0
3 x 7 6
7
x
3
x 1
3
1 7 7 13 1 13
; ; ;
3 3 3 3 3 3
1
3
7
3
1 13
Ответ : ;
3 34
5.
Универсальный способ (по определению модуля)=> если под знаком модуля находится
функция от х, которая может принимать
как отрицательные, так и неотрицательные
значения, то необходимо рассмотреть два
варианта раскрытия для каждого из модулей.
а , если а 0
a
а , если а 0
Пример 2. 3 x 7 6
1 случай.
3 x 7 0
3 x 7 6
7
x
3
x 13
3
7
3
Решением неравенства
является объединение
16.07.2019
решений всех случаев.
2 случай.
13
3
3 x 7 0
3 x 7 6
7
x
3
x 1
3
1
3
7
3
1 13
Ответ : ; ;
3 3 5
6.
Универсальный способ (по определению модуля)а , если а 0
a
а , если а 0
Пример 3. 3 x 7 6 2 x
1 случай.
3 x 7 0
3 x 7 6 2 x
7
x
3
x 13
5
=> если под знаком модуля находится
функция от х, которая может принимать
как отрицательные, так и неотрицательные
значения, то необходимо рассмотреть два
варианта раскрытия для каждого из модулей.
2 случай.
3 x 7 0
3 x 7 6 2 x
7
3
Решением неравенства
является объединение
16.07.2019
решений всех случаев.
13
5
7
x
3
x 1
7
3
1
Ø
7 13
Ответ : ;
3 5
6
7.
Универсальный способ (по определению модуля)а , если а 0
a
а , если а 0
Пример 4. 3 x 7 6 2 x
1 случай.
3 x 7 0
3 x 7 6 2 x
7
x
3
x 13
5
=> если под знаком модуля находится
функция от х, которая может принимать
как отрицательные, так и неотрицательные
значения, то необходимо рассмотреть два
варианта раскрытия для каждого из модулей.
2 случай.
3 x 7 0
3 x 7 6 2 x
7
3
Решением неравенства
является объединение
16.07.2019
решений всех случаев.
13
5
7
x
3
x 1
7
3
1
7 13
Ответ : ; ;
3 5
7
8.
Универсальный способ (по определению модуля)Можно доказать, что решения рассмотренных неравенств могут
быть записаны при помощи следующих альтернативных схем:
f ( x ) g( x )
f ( x ) g( x )
f ( x ) g( x )
f ( x ) g( x )
f ( x ) g( x )
f ( x ) g( x )
f ( x ) g( x )
f ( x ) g( x )
f ( x ) g( x )
f ( x ) g( x )
f ( x ) g( x )
f ( x ) g ( x )
Не пытайтесь запомнить данные равносильные переходы без
понимания их смысла. Сначала выработайте навык используя
предыдущую форму записи.
16.07.2019
Назад
9.
Универсальный способ (по определению модуля)Пример 5. x 3 x 3 x 6
1 случай.
x 3 0
x 3
3
x
6
0
x 2
( x 3 ) x ( 3 x 6 ) x 9
Ø
2 случай.
x 3 0
3 x 6 0
( x 3 ) x ( 3 x 6 )
x 3
x 2
x 3
x ( 3 ; 2 )
9
2
3 случай.
x 3 0
3 x 6 0
( x 3 ) x ( 3 x 6 )
3
3
Представьте, что модулей
в 2
неравенстве три (или
пять)!
4 случай.
x 3
x 2
x 3
3
x 3 0
3 x 6 0
( x 3 ) x ( 3 x 6 )
Ø
3
2
3
Решением неравенства является
объединение решений всех случаев.
2
1
x 3
x 2
x 1
x [ 2 ; 1 )
3
Ответ : ( 3 ; 1 )
10.
Метод интервалов.Если модулей в задаче несколько, то решение предыдущим способом
может оказаться очень перегруженным. Рассмотрим более удобный
для такого случая метод.
1) На числовой прямой отметить нули подмодульных выражений.
2) Определить знак каждого выражения на каждом числовом
промежутке (например, по какому-нибудь значению х из
промежутка, кроме концевых точек).
3) Раскрыть модули на каждом из промежутков и решить
полученное неравенство.
4) Из полученных решений выбрать те, которые данному
промежутку принадлежат.
5) Объединить ответы из всех промежутков.
Назад
11.
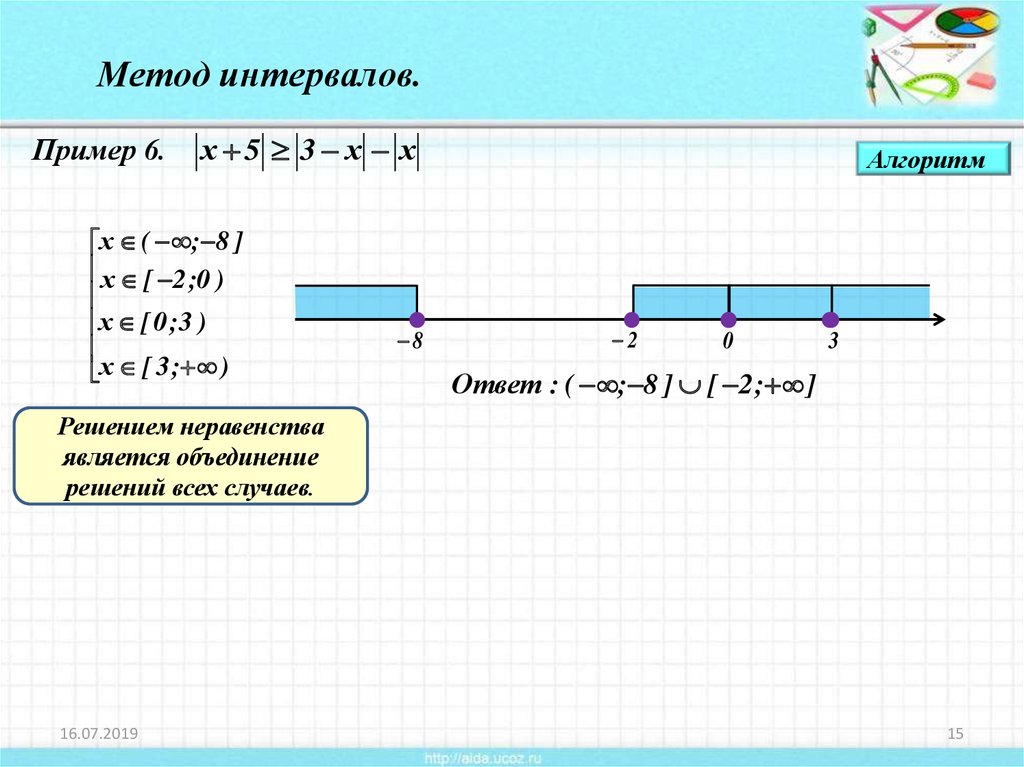
Метод интервалов.Пример 6.
х 5 3 х х
Алгоритм
Нули подмодульных выражений: х 5 ;0 ;3.
х 5
3 х
х
( ; 5 )
[ 5 ;0 )
[ 0 ;3 )
[ 3 ; )
5
0
3
1 случай.
Замечание: концевые точки (нули подмодульных выражений)
х ( ; 5 ) включать в промежутки
х ( ; 5 ) именно таким образом.
не обязательно
можно сделать и по другому.
x 8Главное, чтобы каждая точка
Это
(
х
5
)
(
3
х
)
(
х
)
5
попала в один из рассматриваемых промежутков. 8
х ( ; 8 ]
16.07.2019
11
12.
Метод интервалов.Пример 6.
х 5 3 х х
Алгоритм
Нули подмодульных выражений: х 5 ;0 ;3.
х 5
3 х
х
( ; 5 )
[ 5 ;0 )
[ 0 ;3 )
[ 3 ; )
5
0
3
2 случай.
х [ 5 ;0 )
( х 5 ) ( 3 х ) ( х )
х [ 5 ;0 )
x 2
5
2
0
х [ 2 ;0 )
16.07.2019
12
13.
Метод интервалов.Пример 6.
х 5 3 х х
Алгоритм
Нули подмодульных выражений: х 5 ;0 ;3.
х 5
3 х
х
( ; 5 )
[ 5 ;0 )
[ 0 ;3 )
[ 3 ; )
5
0
3
3 случай.
х [ 0 ;3 )
( х 5 ) ( 3 х ) ( х )
х [ 0 ;3 )
x 2
3
2
3
0
3
х [ 0 ;3 )
16.07.2019
13
14.
Метод интервалов.Пример 6.
х 5 3 х х
Алгоритм
Нули подмодульных выражений: х 5 ;0 ;3.
х 5
3 х
х
( ; 5 )
[ 5 ;0 )
[ 0 ;3 )
[ 3 ; )
5
0
3
4 случай.
х [ 3 ; )
х ( 0 ;3 )
( х 5 ) ( 3 х ) ( х ) x 8
8
3
х [ 3 ; )
16.07.2019
14
15.
Метод интервалов.Пример 6.
х 5 3 х х
х ( ; 8 ]
х [ 2 ;0 )
х [ 0 ;3 )
х [ 3 ; )
8
Алгоритм
2
0
3
Ответ : ( ; 8 ] [ 2 ; ]
Решением неравенства
является объединение
решений всех случаев.
16.07.2019
15
16.
Метод интервалов.2
2
Пример 7. х 2 x 2 х х x x( х 2 ) 2 х x( х 1 )
Нули подмодульных выражений: х 2 ;0 ;1;2.
x( x 2 )
2 х
х( x 1 )
1 случай.
( ; 2 )
[ 2 ;0 )
0
2
Алгоритм
[ 0 ;1 )
[ 1; 2 )
[ 2 ; )
2 случай.
1
2
х ( ; 2 )
2
2
(
х
2
x
)
(
2
х
)
(
x
х)
х [ 2 ;0 )
2
2
(
х
2
x
)
(
2
х
)
(
x
х)
х ( ; 2 )
x 0 ,5
х [ 2 ;0 )
2
x 1 0 - верно при любом х
2
х ( ; 2 )
16.07.2019
0 ,5
х [ 2 ;0 )
16
17.
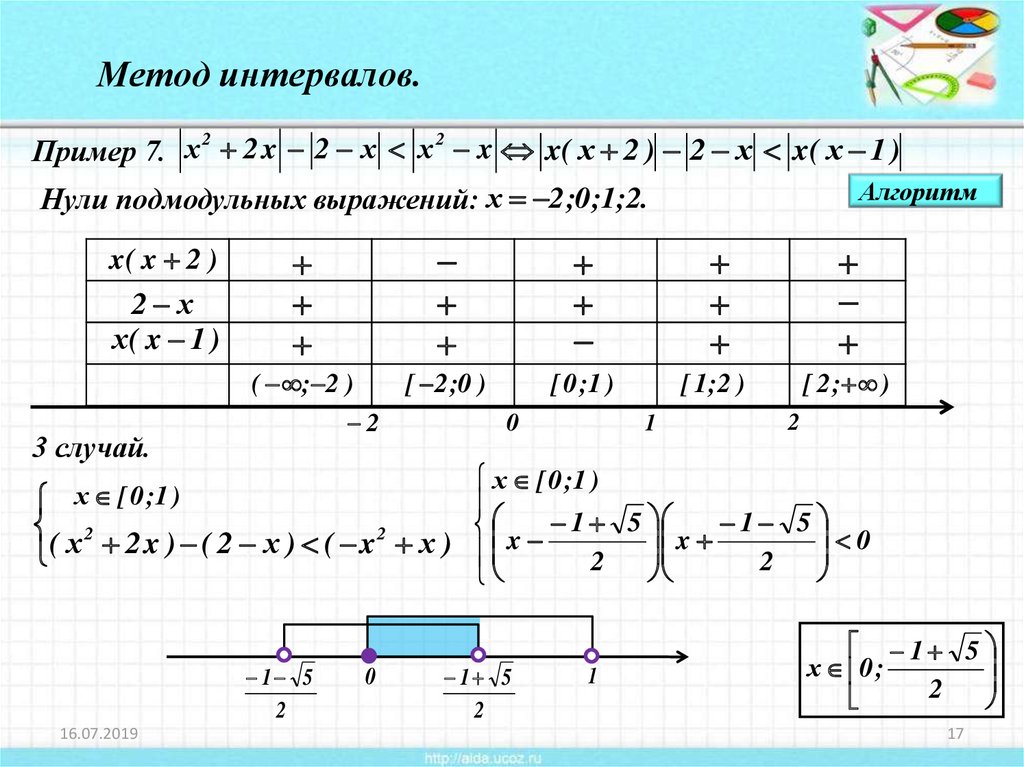
Метод интервалов.2
2
Пример 7. х 2 x 2 х х x x( х 2 ) 2 х x( х 1 )
Алгоритм
Нули подмодульных выражений: х 2 ;0 ;1;2.
x( x 2 )
2 х
х( x 1 )
3 случай.
( ; 2 )
[ 2 ;0 )
0
2
[ 0 ;1 )
[ 1; 2 )
[ 2 ; )
1
2
х [ 0 ;1 )
( х 2 2 x ) ( 2 х ) ( x 2 х ) x 1 5 x 1 5 0
2
2
х [ 0 ;1 )
1 5
2
16.07.2019
0
1 5
2
1
1 5
х 0 ;
2
17
18.
Метод интервалов.2
2
Пример 7. х 2 x 2 х х x x( х 2 ) 2 х x( х 1 )
Алгоритм
Нули подмодульных выражений: х 2 ;0 ;1;2.
2 х
х( x 1 )
4 случай.
x( x 2 )
( ; 2 )
[ 2 ;0 )
0
2
[ 0 ;1 )
[ 1; 2 )
[ 2 ; )
5 случай.
1
2
х [ 1; 2 )
2
2
(
х
2
x
)
(
2
х
)
(
x
х)
х [ 2 ; )
2
2
(
х
2
x
)
(
2
х
)
(
x
х)
х [ 1; 2 )
x 0 ,5
х [ 2 ; )
x 1
16.07.2019
0 ,5
1
2
Ø
1
2
Ø
18
19.
Метод интервалов.2
2
Пример 7. х 2 x 2 х х x
х ( ; 2 )
х [ 2 ;0 )
1 5
х
0 ;
2
Решением неравенства
является объединение
решений всех случаев.
2
Алгоритм
0
1 5
2
1 5
Ответ : ;
2
Рассмотрим возможные неприятности, которые могут возникнуть
при использовании метода интервалов.
16.07.2019
19
20.
Метод интервалов (неприятности).Пример 8. x 2 x 8 x
x x 8 ( )0 ?
1 случай.
1 33 1 33
х
;
2 2
x2 x 8 x
8
8
1 33
2
16.07.2019
2
1 33
2
1 33
2
1 33
2
1 33 1 33
х
;
2 2
( x 8 )( x 8 ) 0
1 33
8?
2
1 33
8?
2
Как
сравнить?
1 33
х 8 ;
2
20
21.
Метод интервалов (неприятности).Пример 8. x 2 x 8 x
x x 8 ( )0 ?
1 33
2
2 случай.
1 33 1 33
x 2 ; 2
x2 x 8 x
11 33
33
22
2
4
11 33
33
22
1 33
2
1 33 1 33
x 2 ; 2
( x 4 )( x 2 ) 0
2
1 33
4?
2
1 33
2?
2
Как
сравнить?
1 33
Ответ : х
; 2
2
21
22.
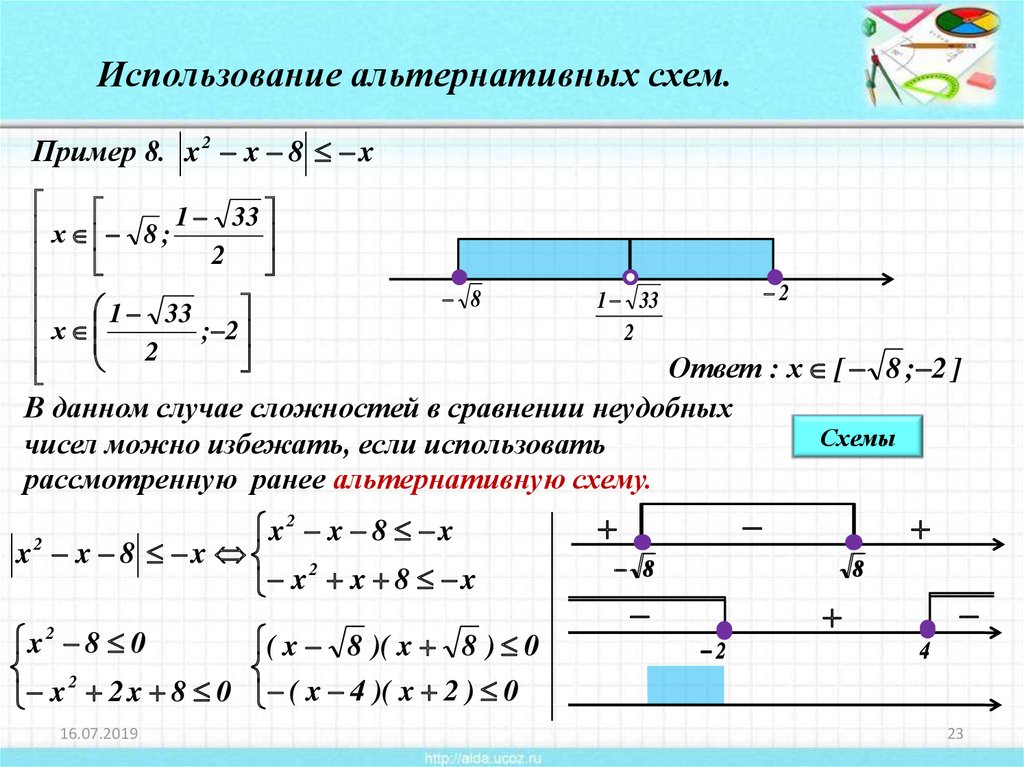
Использование альтернативных схем.Пример 8. x 2 x 8 x
1 33
х 8 ;
2
1 33
х
;
2
2
8
2
1 33
2
Ответ : х [ 8 ; 2 ]
В данном случае сложностей в сравнении неудобных
Схемы
чисел можно избежать, если использовать
рассмотренную ранее альтернативную схему.
2
x
x 8 x
2
x x 8 x 2
x x 8 x
x 8 0
( x 8 )( x 8 ) 0
2
x 2 x 8 0 ( x 4 )( x 2 ) 0
2
16.07.2019
8
8
2
4
23
23.
Использование альтернативных схем.Предыдущее неравенство, хоть и с трудностями, но все же вполне
решаемо методом интервалов. Рассмотрим неравенство, которое
маловероятно решить этим методом.
Пример 9. x7 4 x 5 x 2 2 x 3 x7 4 x 5 x 2 2 x 3
x7 4 x 5 x 2 2 x 3 x7 4 x 5 x 2 2 x 3
7
5
2
7
5
2
x 4x x 2x 3 x 4x x 2x 3
2 x2 4 x 6 0
7
5
2 x 8 x 0
( x 1 )( x 3 ) 0
2
5
2
2 x ( x 4 ) 0 ( x 4 ) 0
( x 1 )( x 3 ) 0
5
2x 0
16.07.2019
3
Схемы
1
0
Ответ : х ( ;0 ) ( 1; )
24
24.
Использование свойств модулей.Свойства модулей, которые могут значительно упрощать решение
некоторых задач.
2
2
1. a 0 ; 2. a a ; a a ; 3. a a ; 4. a a ; 5. a b a b .
Пример 10.
1 x 1 x x 2 1 ( 1 x )( 1 x ) x 2 1 (5 свойство)
1 x2 x2 1
Ответ : x R (2 свойство)
Пример 11. x 2 8 x 7 ( 2 x 2 3 x 5 ) 0
x 2 8 x 7 0 (1 свойство)
Если x 2 8 x 7 0 , то неравенство выполнено x 1, x 7 - решения
Если x 2 8 x 7 0 , то можно обе части неравенства разделить на
положительный множитель сохранив знак неравенства.
2 x2 3x 5 0
2( x 1 )( x 2 ,5 ) 0
1
1
2 ,5
7
Ответ : x [ 1;2 ,5 ] { 7 }
25.
Использование свойств модулей.Свойства модулей, которые могут значительно упростить решение задач.
2
2
1. a 0 ; 2. a a ; a a ; 3. a a ; 4. a a ; 5. a b a b .
3x 1
3x 1
Пример 12. 1 x
0 x 1
0 (3 свойство)
x 3
x 3
ОДЗ : x 3
x 1 ( x 3) 3 x 1
x 3
( x 1 )x
x 3
0
0 (5 свойство)
x 1 ( x 3) 3)
x 3
0
x 1 x
x 3
0
Если ( x 1 ) x 0 , то неравенство
выполнено x 1, x 0 - решения
Если ( x 1 ) x 0 , то можно обе части неравенства разделить на
положительный множитель сохранив знак неравенства.
x 3
1
0 x 3 0
1
3
0
3
x 3
x 3
Ответ : x ( 3 ;3 )
26.
Использование свойств модулей.Свойства модулей, которые могут значительно упростить решение задач.
2
2
1. a 0 ; 2. a a ; a a ; 3. a a ; 4. a a ; 5. a b a b .
Пример 13. x 2 x 3 0 x 2 x 3 0 (4 свойство)
Введем переменную: x a
2
2
a 2 2 a 3 0 ( a 3 )( a 1 ) 0
a 1
a 3
x 1 Ø
x 3 Схемы
x 3
x 3
x 3
3
1
3
3
Ответ : x ( ; 3 ) ( 3 ; )
27.
Метод замены множителей.Пример 14.
3x 2 2x 3
x x 8 x x
2
2
0
Очевидно, что свойства модулей нам в данном случае не помогут.
Решать методом интервалов страшновато. Хотя долгая и
кропотливая работа безусловно даст результат. Но, чем больше
действий вам придется выполнить, тем больше вероятность
устать и допустить ошибку.
Существует более простое и красивое решение.
Теорема : неравенство f(x) ≥ g(x) при f(x) ≥0 и g(x) ≥0 равносильно
неравенству f²(x) ≥ g²(x), т.е. неравенство f(x) - g(x) ≥ 0
равносильно неравенству f²(x) - g²(x) ≥ 0.
Другими словами: знак выражения f(x)-g(x) при условии, что f(x)≥0
и g(x)≥0 совпадает со знаком выражения f2(x)-g2(x).
28.
Метод замены множителей.Несколько примеров замены множителей при решении неравенств
с модулями.
Множитель
f ( x ) g( x )
f ( x ) g( x )
f ( x ) g( x )
s( x ) h( x )
f ( x ) g( x )
s( x ) h( x )
Замена
f 2( x ) g2( x )
f 2 ( x ) g 2 ( x ), если g ( x ) 0
f 2( x ) g2( x )
s 2 ( x ) h2 ( x )
f 2( x ) g2( x )
, если
2
2
s ( x ) h ( x )
g( x ) 0
h( x ) 0
29.
Метод замены множителей.Пример 14.
3x 2 2x 3
x x 8 x x
2
2
0
(( 3 x 2 ) ( 2 x 3 ))(( 3 x 2 ) ( 2 x 3 ))
( 3 x 2 )2 ( 2 x 3 )2
0
2
0
2
2
2
2
2
2
2
(( x x 8 ) ( x x ))(( x x 8 ) ( x x ))
( x x 8) ( x x)
( 3 x 2 2 x 3 )( 3 x 2 2 x 3 )
( x 1 )( 5 x 5 )
0
0
2
2
2
2
2
( x x 8 x x )( x x 8 x x )
( 2 x 8 )( 2 x 8 )
( x 1 )( x 1 )
0
( x 4 )( x 2 )( x 2 )
2
1
1
2
4
Ответ : x ( ; 2 ) [ 1;1 ] ( 2 ;4 )
30.
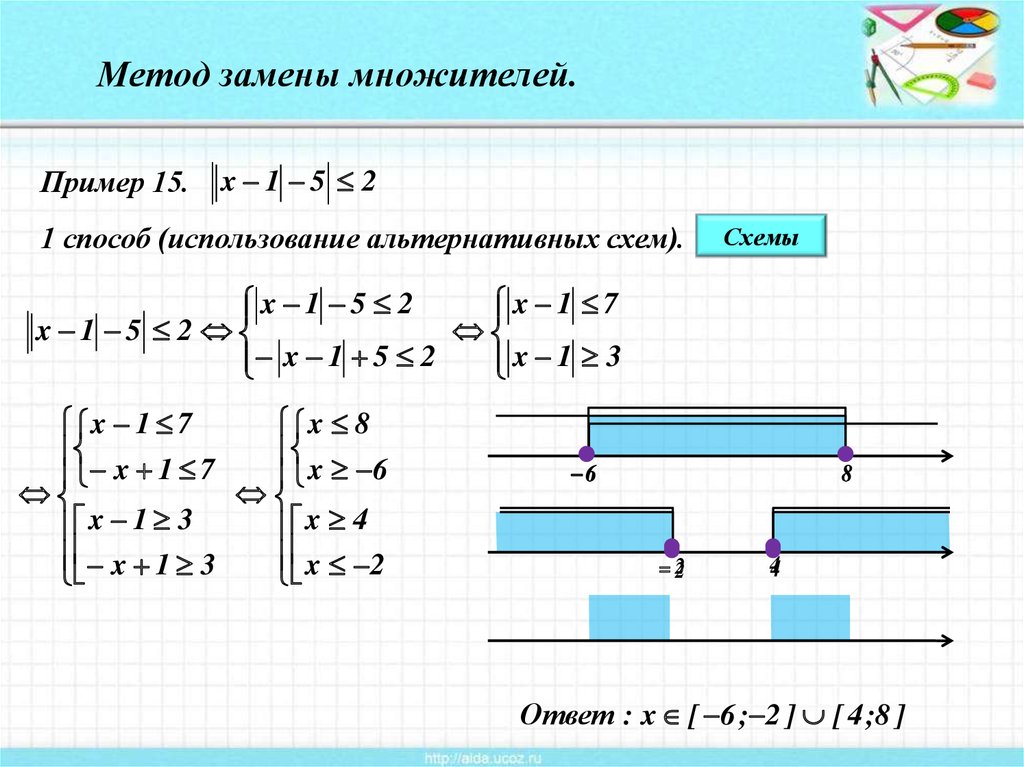
Метод замены множителей.Пример 15.
x 1 5 2
1 способ (использование альтернативных схем).
Схемы
x 1 5 2
x 1 7
x 1 5 2
x 1 5 2
x 1 3
x 1 7
x 8
x 1 7
x 6
x 1 3
x 4
x 1 3
x 2
6
8
2
4
Ответ : x [ 6 ; 2 ] [ 4 ;8 ]
31.
Метод замены множителей.Пример 15.
x 1 5 2
2 способ (замены множителей).
2
2
x 1 5 2 0 ( x 1 5 ) 2 0 (( x 1 5 ) 2 )(( x 1 5 ) 2 ) 0
( x 1 7 )( x 1 3 ) 0 (( x 1 )2 7 2 )(( x 1 )2 32 ) 0
(( x 1 ) 7 )(( x 1 ) 7 )(( x 1 ) 3 )(( x 1 ) 3 ) 0
( x 8 )( x 6 )( x 4 )( x 2 ) 0
В рассмотренной задаче
метод замены множителей
не упростил решение.
Вывод: старайтесь использовать
те или иные методы разумно!
6
2
4
8
Ответ : x [ 6 ; 2 ] [ 4 ;8 ]
32.
Метод замены множителей.f ( x ) g( x )
А если g(x)<0? (Вполне возможно при решении задач.)
В этом случае имеем сумму неотрицательного и положительного
выражений. Неотрицательный множитель не влияет на знак
произведения => на него можно разделить обе части неравенства не
меняя его знак.
В этом случае можно считать верной замену:
f ( x ) g( x ) 1
Для простоты – 1. А вообще – любое положительное число.
2
2
Пример 16. x 2 x 2 x 1 0 x 2 x ( 1 2 x ) 0
Выражение в скобке может принимать как неотрицательные,
так и отрицательные значения. Следовательно необходимо
рассмотреть два случая с разными заменами.
33.
Метод замены множителей.f ( x ) g( x ) 1, при g(x)<0
2
Пример 16. x 2 x 2 x 1 0
x 2x ( 1 2x ) 0
2
f ( x ) g( x ) f 2 ( x ) g 2 ( x ), при g(x)≥0
1 случай. 1 2 x 0
x 0 ,5
Замена : x 2 2 x ( 1 2 x ) ( x 2 2 x )2 ( 1 2 x )2
(( x 2 2 x ) ( 1 2 x ))(( x 2 2 x ) ( 1 2 x )) 0
( x 2 1 )( x 2 4 x 1 ) 0
1
( x 1 )( x 1 )( x ( 2 3 ))( x ( 2 3 )) 0
2 случай. x 0 ,5
Замена : x 2 2 x ( 1 2 x ) 1
1 0 Ø
2 3
0 ,5
1
2 3
х ( 1;2 3 )
Ответ – объединение решений
первого и второго случая.
Ответ : х ( 1;2 3 )
34.
Тренировочные упражнения.x2 3 2 x
Ответ : x ( ; 3 ] [ 3 ; )
7
x 1 4 x 4 Ответ : x ;
2
3 x 2 2 x Ответ : x [ 1; )
9 17
2
2
x 6 x 8 3 x x Ответ : x ;
4
x 2 1 x 1 0 Ответ : x { 1 } [ 0 ;2 ]
3x x 3
1
x 2
x2 2 x 2 x 1
x x x 3x
2
2
8
;
3
1
Ответ : x ( ; 2 ) ;
3
0 Ответ : x ( ; 1 ) ( 2 3 ; )
35.
ИсточникиА. С. Зеленский, И. И. Панфилов «Решение уравнений и неравенств с
модулем»
http://narod.ru/disk/11487224001/%D0%97%D0%B5%D0%BB%D0%B5%D0%BD%D1%81%D0%BA%D0%B8%D0%B9%
2C%20%D0%9F%D0%B0%D0%BD%D1%84%D0%B8%D0%BB%D0%BE%D0%B2.%20%D0%9C%D0%BE%D0%B4%D1%83
%D0%BB%D0%B8.djvu.html
КИМ ЕГЭ 2013 года
http://alexlarin.net/ege/2013/c3_2013.html
П. Н. Севрюков, А. Н. Смоляков «Уравнения и неравенства с
модулями и методика их решения» http://alexlarin.com/viewtopic.php?f=27&t=8605






























 Математика
Математика








