Решение дробно-рациональных уравнений с параметром

1. Тема урока: Решение дробно-рациональных уравнений с параметром

Цели:
1. Обобщить, углубить знания школьников по изучаемой теме.
2. Способствовать формированию умений применять приемы сравнения,
обобщения, выделения главного, переноса знаний в новую ситуацию; развитию
творческих способностей учеников путем решения заданий, содержащих
модули, параметры.
3. Побуждать учеников к самоконтролю, взаимоконтролю, самоанализу своей
учебной деятельности.
Оборудование: экран, АРМ
Урок формирования знаний и умений
Учитель Зубкова В.В.

2.

Решить уравнение с параметром – это
значит показать, каким образом для любого
значения параметра можно найти
соответствующее множество корней уравнения,
если корни существуют, или установить, что
при этом значении параметра корней нет.

3. I. Как решить дробно рациональное уравнение?

Найти общий знаменатель дробей
Умножить обе части уравнения на общий
знаменатель
Решить целое уравнение
Исключить из его корней те, которые
обращают в нуль общий знаменатель
Записать ответ.

4. II. Решить устно

1)При каких значениях x имеет смысл
выражения:
2) Решите уравнение:
3)Решите уравнения :
x
2
9 x 20
0
x 5
x2
1
x 1 x 1

5.

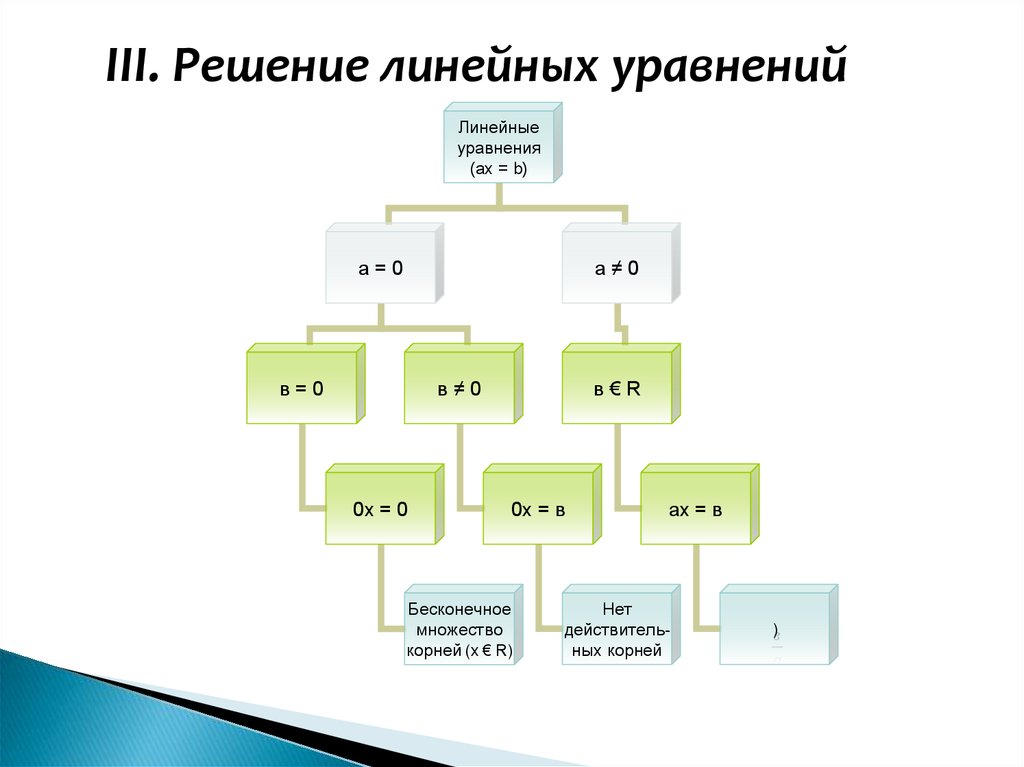
III. Решение линейных уравнений
Линейные
уравнения
(ах = b)
а=0
а≠0
в=0
в≠0
0х = 0
в€R
0х = в
Бесконечное
множество
корней (х € R)
ах = в
Нет
действительных корней
)в
а

6. Установить связь

1. 2 (х + 7) = 2х + 14
2. 3 (х – 1) – 3 (5 + х) = 7
3. (а2 – 9) х = а2 – 5а + 6
2х 5 х
4.
х
3
2

7. Установить связь

1. х2 + ах + 12 = 0
2. ах2 – 2х + 4 = 0
3. 2х2 + 4х + а = 0

8. Решите квадратное уравнение х2 -(2а+1)х+а2+а-2=0

Всегда ли это уравнение
квадратное?
Да, это уравнение всегда
квадратное.

9. Найдите дискриминант уравнения.

10. Примените формулу корней квадратного уравнения.

Ответ: х1=а+2; х2=а-1.

11. Решите уравнение: ах2+(1-а)х -1=0.

Всегда ли это уравнение
квадратное?

12.  

13. Примените формулу корней квадратного уравнения.

14. Запишите ответ.

15.  

16. Алгоритм решения «квадратного» уравнения с параметром

1.Найти значения параметра, при которых
уравнение не является квадратным
(коэффициент при х2 равен нулю).
2.Решить уравнение при этих значениях
параметра.
3.Найти дискриминант уравнения в
остальных случаях.
4.Найти корни уравнения при всех
значениях параметра.

17. Самостоятельная работа

Один из корней квадратного уравнения х2 +2ах+23а=0 равен 1. Найдите значение параметра а и
второй корень уравнения.
Алгоритм решения «квадратных» уравнений с параметром
1.Найти значения параметра, при которых уравнение не является
квадратным (коэффициент при х2 равен нулю).
2.Решить уравнение при этих значениях параметра.
3.Найти дискриминант уравнения в остальных случаях.
4.Найти корни уравнения при всех значениях параметра.

18.

Рефлексия
Я - понял…
Я – знаю…
Я – умею…