Показательная функция

1. Показательная функция

Алфимова Анастасия Андреевна
МБУ СОШ №72
Г. Тольятти

2. Цель урока

обучающий аспект:
ввести понятие показательной функции;
учить строить график показательной функции;
рассмотреть свойства показательной функции;
развивающий аспект:
развивать грамотную математическую речь при
ответе с места и у доски;
развивать мышление посредством:
анализа и синтеза при работе над выводом
алгоритма
постановки и решения проблемы (логические
умозаключения при возникновении проблемной
ситуации и ее разрешении);
воспитывающий аспект:
воспитывать соблюдение норм поведения в
коллективе, уважение к мнению окружающих при
совместной деятельности в группах.

3. Реальные процессы

Радиоактивный
распад
Вид
функция
m m0 2
t
T
Рост
Барометричес
народонаселени кая формула
я
N N 0e
t
р р0 е
h
H

4. Задание №1

1 группа
2 группа
Схематично изобразить
график функции
у 2
х
1
у
2
х

5.

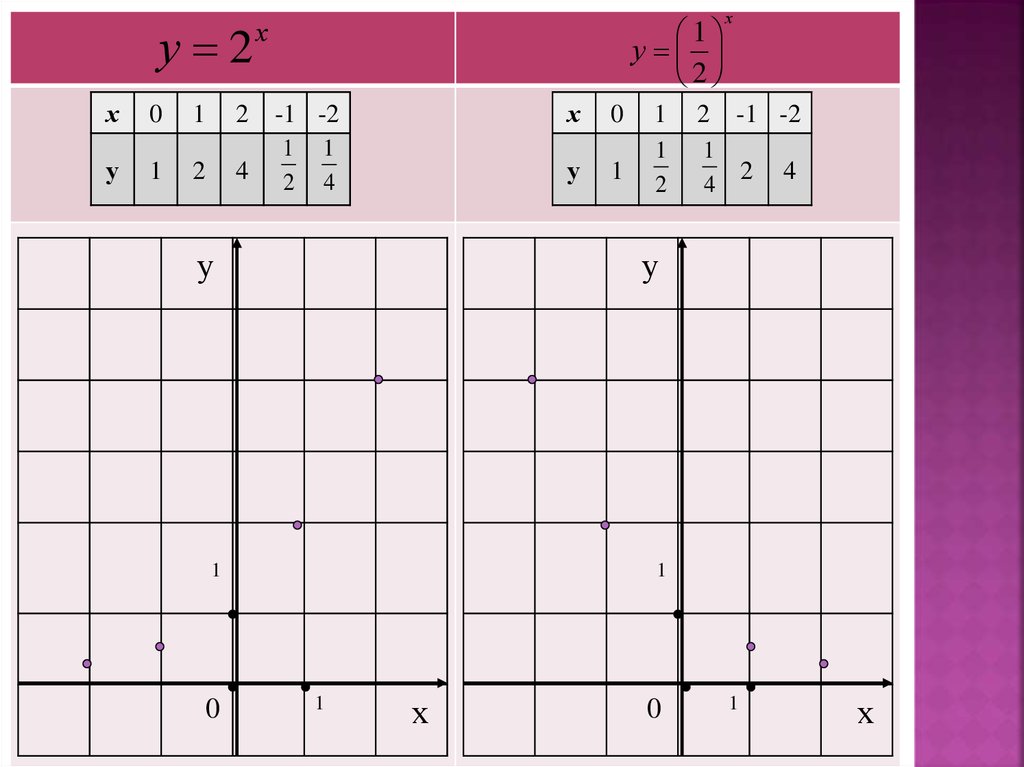
у 2
х
у
0
1
1
2
2
4
1
у
2
х
х
-1 -2
1
2
1
4
у
у
0
1
2
-1 -2
1
1
2
1
4
2
4
у
1
0
х
1
1
х
0
1
х

6.

22 4
1
2
2 2 1,41421356237
2
3
?
Зная, что 3 = 1,7320508...
Если мы рассмотрим последовательность
рациональных чисел – десятичных
приближений числа по недостатку или
по избытку, мы докажем, что эта
последовательность сходится, значит
х
функция у 2 непрерывна на
множестве действительных чисел.
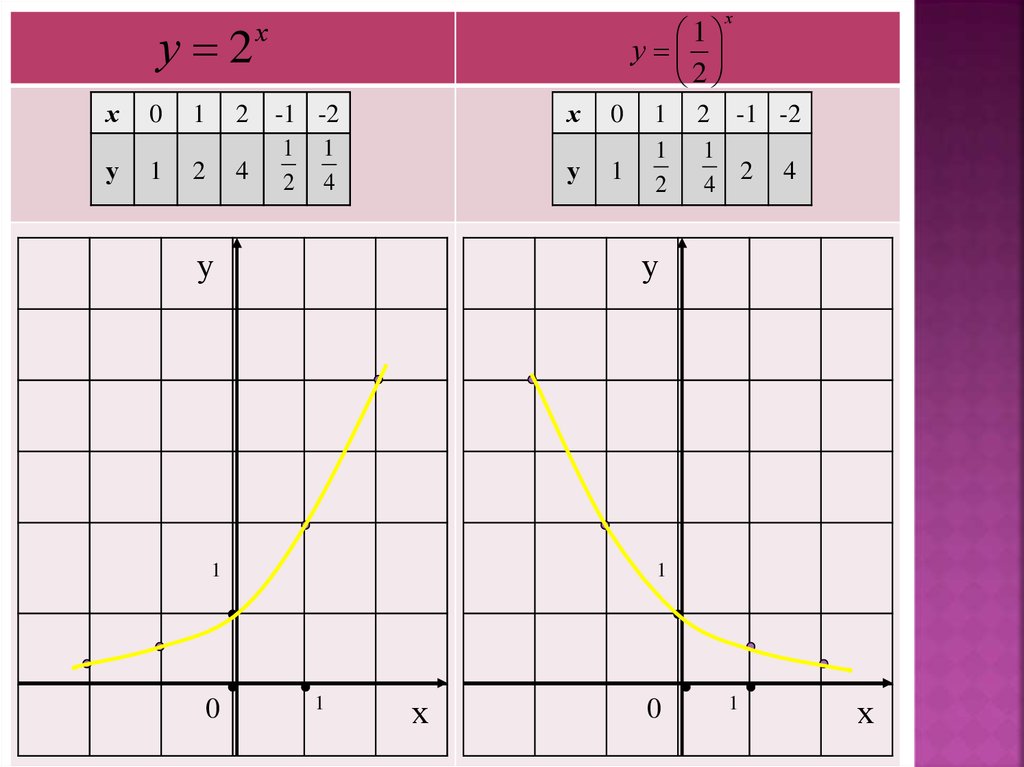
Поэтому мы можем соединить эти точки
и получим график показательной
функции.

7.

у 2
х
у
0
1
1
2
2
4
1
у
2
х
х
-1 -2
1
2
1
4
у
у
0
1
2
-1 -2
1
1
2
1
4
2
4
у
1
0
х
1
1
х
0
1
х

8. Определение показательной функции

Функция, заданная формулой y = ax
(a > 0, а ≠ 1, х R), называется
показательной функцией.

9. Легенда о шахматах

Впервые легенда о награде за изобретении шахмат
встречается в ХI веке н.э. в книге арабского
учёного Аль Бируни.
Она гласит о том, что
за первую клетку шахматной доски изобретатель
потребовал от царя 1 пшеничное зернышко,
за вторую клетку – 2,
за третью – 4,
за четвертую – 8 и т.д.
И для того чтобы найти сколько же потребовал
изобретатель, нужно сложить члены
геометрической прогрессии: 1, 2, 4, 8, …, 263. Эта
сумма равна 264 – 1, т.е. 184467440737095551615.

10. История возникновения показательной функции

В дальнейшем появляются в Западной Европе (это
ХIV – XV в.) банки, которые давали деньги под
большие проценты. И при этом приходилось
делать большие, сложные расчеты.
Вскоре появляется идея степени с дробным
показателем, потом создаются таблицы
логарифмов и антилогарифмов.
Оставался один шаг, чтобы ввести степени с
любым действительным показателем. И этот шаг, в
конце концов, был сделан в конце XVII в. Исааком
Ньютоном.
И уже после этого Иоганн Бернулли рассмотрел
степени с переменным действительным
показателем, т.е. ввёл показательную функцию.

11.

Среди
заданных функций укажите
те, которые являются
показательными:
а) y = 3х
б) y = х3
3
в) y = х 5
г) y = ( 3)
х

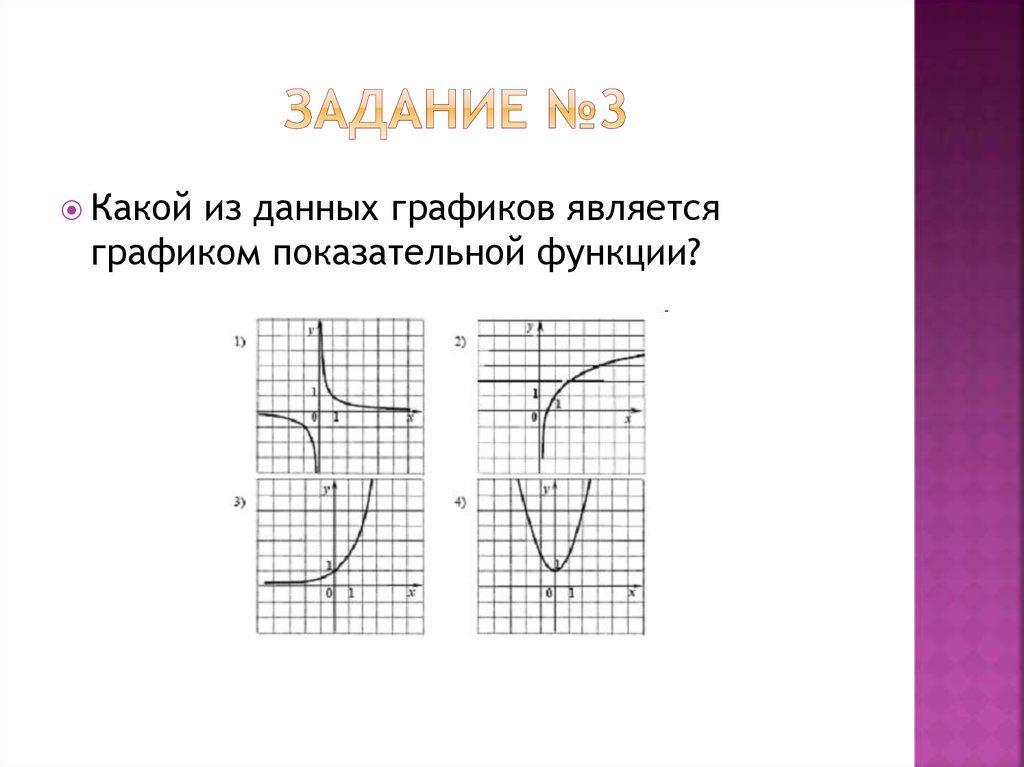
12. Задание №3

Какой
из данных графиков является
графиком показательной функции?

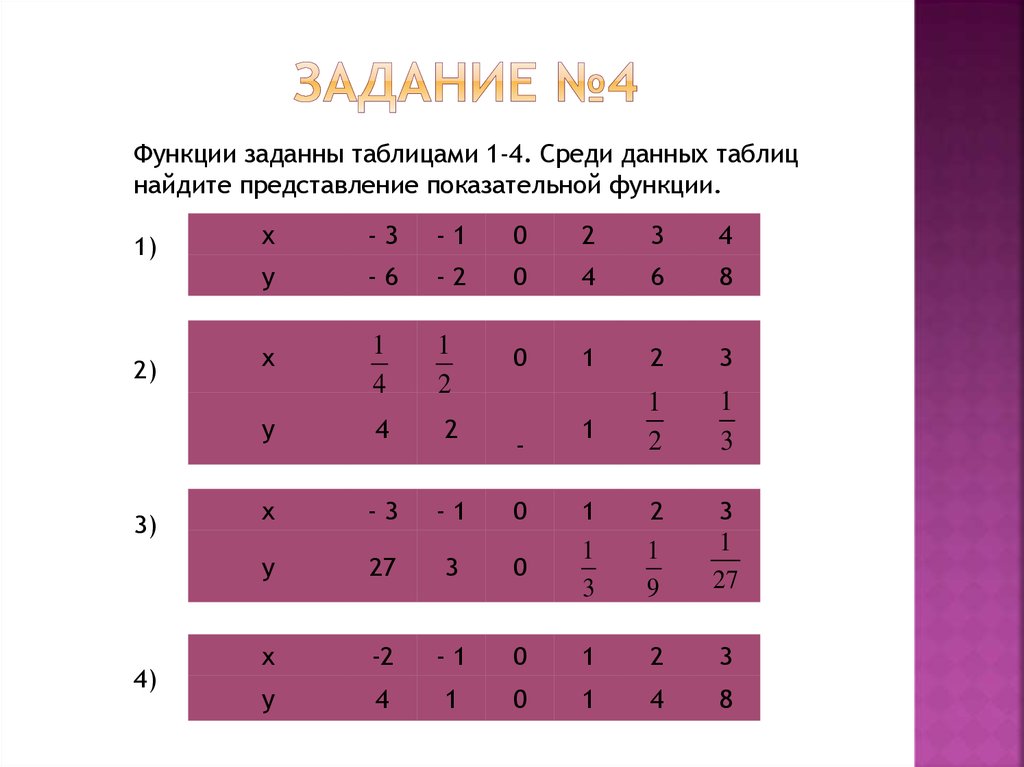
13. Задание №4

Функции заданны таблицами 1-4. Среди данных таблиц
найдите представление показательной функции.
1)
2)
3)
4)
x
-3
-1
0
2
3
4
y
-6
-2
0
4
6
8
x
1
4
1
2
0
1
2
3
y
4
2
1
1
2
1
3
x
-3
-1
0
1
2
y
27
3
0
1
3
1
9
3
1
27
x
-2
-1
0
1
2
3
y
4
1
0
1
4
8
-

14. Задание №5

Заполните
пропуски.
Функцию вида y = ax , где ____ и _____,
называется показательной функцией.

15. Задание №5

Найдите
значение показательной функции
при заданных значениях х:
a ) y 7 х , x1 3, x2 1, x3
1
;
2
х
3
1
1
б ) у , х1 1, х2 , х3 ;
2
2
2
в) у
3 , х
х
1
х
0, х2 4, х3 5;
3
4
г ) у , х1 , х2 1, х3 2,5.
2
9