Похожие презентации:
Определение показательной функции
1. Определение показательной функции
• Показательной функцией называется функциях
у = а , где а – заданное число, а>0,a ≠ 1.
Примеры:
х
1
у
3
у 0, 4
х
у 2
у 5
х
у
3
х
х
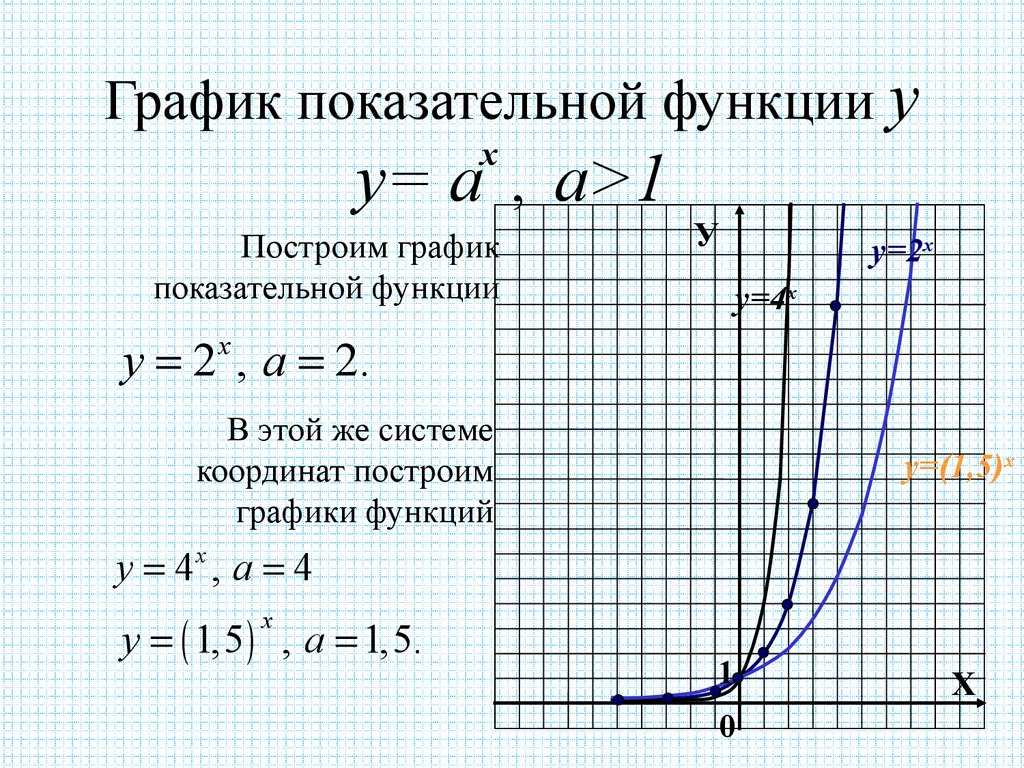
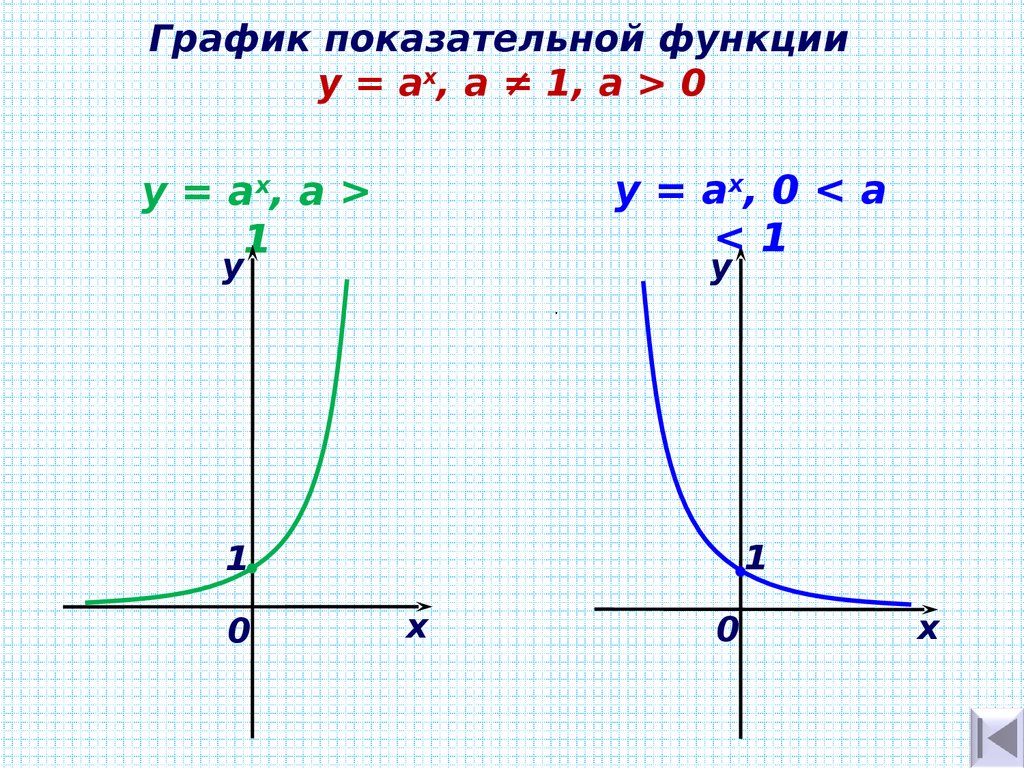
2. График показательной функции у у= а , а>1
График показательной функции ух
у= а , а>1
Построим график
показательной функции
У
у=2х
у=4х
у 2 , а 2.
х
В этой же системе
координат построим
графики функций
у=(1,5)х
у 4 , а 4
х
у 1,5 , а 1,5.
х
1
0
Х
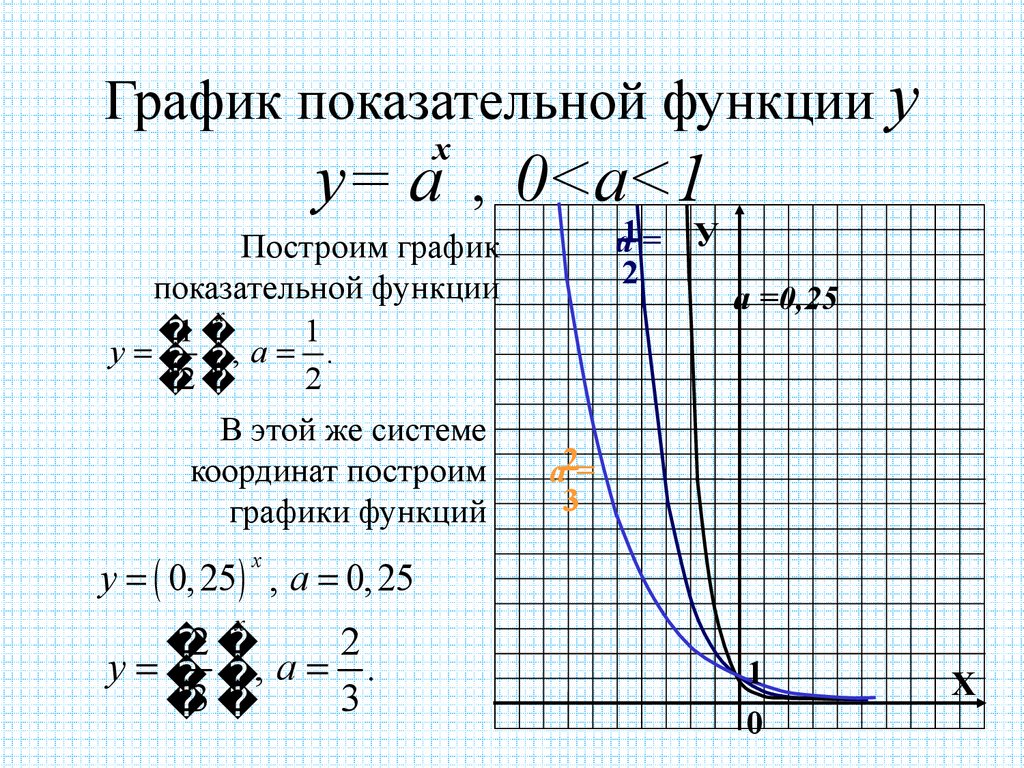
3. График показательной функции у у= а , 0<a<1
График показательной функции ух
у= а , 0<a<1
Построим график
показательной функции
х
1
1
у , а .
2
2
В этой же системе
координат построим
графики функций
а1 = У
2
а =0,25
а2=
3
у 0, 25 , а 0, 25
х
х
2
2
у , а .
3
3
1
0
Х
4. Свойства показательной функции y = ах, а ≠ 1, a > 0
Свойства показательной функции y = ах, а ≠1, a > 0
D(y) = (-∞; +∞),
E(y) = (0; +∞).
2. а) Нулей не имеет;
б) точка пересечения с осью ординат (0; 1),
т. к. у(0) = а0 = 1.
3. а) При а > 1 функция возрастает на R;
.
б) при 0 < а < 1 функция убывает на R.
4. Ни четная функция, ни нечетная.
5. Не ограничена сверху, ограничена снизу.
6. Не имеет ни наибольшего, ни наименьшего значений.
7. Непрерывна. Выпукла вниз.
8. an ∙ am = an + m
an : am = an − m
(an)m = anm
(ab)n = an ∙ bn
(a : b)n = an : bn
5. График показательной функции y = ах, а ≠ 1, a > 0
График показательной функцииy = ах, а ≠ 1, a > 0
y = ах, 0 < а
<1
y = ах, а >
1
у
у
.
1
1
0
х
0
х
6. Свойства сравнения выражений вида ах, а ≠ 1, a > 0
Свойства сравнения выражений вида ах, а ≠1, a > 0
1. Если 0 < а < 1 или а > 1, то равенство ar = as
справедливо тогда и только тогда, когда r = s.
2. Если 0 < а < 1, то
a) неравенство ax > 1 справедливо ⟺ x < 0;
.
б) неравенство ax < 1 справедливо
⟺ x > 0.
3. Если а > 1, то
a) неравенство ax > 1 справедливо ⟺ x > 0;
б) неравенство ax < 1 справедливо ⟺ x < 0.
4. Если а > 1, то
a) неравенство af(x) > ah(x) справедливо ⟺ f(x) > h(x);
б) неравенство af(x) < ah(x) справедливо ⟺ f(x) < h(x).
5. Если 0 < а < 1, то
a) неравенство af(x) > ah(x) справедливо ⟺ f(x) < h(x);
б) неравенство af(x) < ah(x) справедливо ⟺ f(x) > h(x).
7. Показательные уравнения
Уравнения вида af(x) = аh(х), где а ≠ 1, a>0
называют показательными уравнениями
⟺
af(x) = аh(х)
f(x) =
h(х)
Методы решения показательных уравнений:
1. Функционально-графический
метод.
2. Метод уравнивания показателей.
3. Метод введения новой
8. Показательные уравнения. Примеры
Пример 12x 4
2
64
22x 4 26
2x 4 6
x 5
Ответ : 5
Пример 2
1
3
2 x 3,5
Пример 3
5
1
3
2 x 3,5
1
1
3
3
2x 3,5 0,5
x 2
Ответ : 2
x 2 3 x
5 3 x 8
x 2 3x 3x 8
0,5
x 2 6x 8 0
x1 2,
x 4
2
Ответ : 2; 4
9. Показательные уравнения. Примеры
Пример 40,2
x 0,5
5
1
5
5
4x 2х 1 24 0
5 0,04 x 2
x 0,5
0,5 x 0,5
Пример 5
:5
0,5
1
5
25
5 5
5 x 51 2x 4
2 x 2
x 2
2
2
2 х
2 2х 24 0
х 2
2 2х 24 0
Пусть 2х t , где t 0 тогда
t 2 2t 24 0
5 x 55 2 x
t1 6,
t 4
2
x 5 2x
t1 6 не уд ет условию t 0
x 5
Вернемся к исходной переменной
Ответ : 5
2х 4
х 2
Ответ : 2
10. Показательные уравнения. Примеры
Пример 62 x х 2 2
2
5
2x
2
x х 2 2
Пусть 2
5
2
t t 6 0
2
3
t
,
1
2
t 2 4
х 2 2
ОДЗ :
6
х2 2 0
t, t 0
х2 2
х 2
х ( ; 2 ] [ 2 : )
3
не уд ет условию t 0
2
Вернемся к исходной переменной
t1
2
x х 2 2
4
2
x х 2 2
2
x х2 2 2
х2 2 2 х
х 2 2 4 4х х 2
4х 6
х 1,5
2
Ответ : 1,5.
11. Показательные уравнения. Примеры
Пример 7х
64 х 23 х 3 12 0
6
х
3х 3
х
6
х
3
2 2
2 2
6
х
3
х
12 0
12 0
3
х
2 8 2 12 0
3
х
Вернемся к исходной переменной
3
х
2 2
3
1
х
или
х 3
Пусть 2 t , t 0
t 2 8t 12 0
t1 2,
t 6;
2
3
Ответ : 3;
.
log 2 6
3
х
2 6
3
log 2 6
х
3
х
log 2 6
12. Показательные уравнения. Примеры
2х
3
2
9х 2 9
81
27 х
2
х
2
9
9
9
9
2
81
3
27
27 х
9
2 9х 9
9
27 х 2 9 х 9 0
9 27
Пример 8
Вернемся к исходной переменной
3х 3
х 1
Пусть 3 х t , где t 0, тогда
t 3 2t 2 9 0
t 3 3t 2 t 2 9 0
t 2 t 3 t 3 t 3 0
t 3 t 2 t 3 0
t 3
2
t t 3 0 нет корней
Ответ : 1.
13. Показательные уравнения. Примеры
Пример 9 (однородное уравнение)52x 1 13 15 х 54 9 х 1 0
5 5
2x
5 52x
9х
13 15 54
0
9
13 15 х 6 9х 0
х
Разделим на 9х , тогда
5 5
9х
2x
5
5
3
2х
х
х
13 15
6 9
0
х
х
9
9
х
5
13 6 0
3
5t 2 13t 6 0
3
t1 5 ,
t 2 2
Вернемся к исходной переменной
х
х
3
5
5
3
х 1
или
5
2
3
х log 5 2
3
х
5
Пусть t , где t 0, тогда
3
Ответ : 1; log 5 2.
3
14. Показательные уравнения. Примеры
Пример 10 (составление отношения)4 x 3 х 1 4 х 1 3x
4 x 4 х 1 3 x 3x 1
4 x 1 4 1 3x 1 3 1
4 x 1 3 3x 1 4
: 3 х 1 3 , т.к . 3х 1 3 0
4x 1 3 3x 1 4
х 1
х 1
3 3 3 3
x 1
4
4
3
3
x 1 1
x 2
Ответ : 2.
15. Показательные уравнения. Примеры
+Показательные уравнения.
Примеры
=4
Пример 11 (скрытая замена переменной)
x
x
2 3 2 3 4
Заметим , что 2 3 2 3
2 3 2 3
4 3 1
х
х
1
1
Пусть 2 3 t , где t 0, тогда 2 3
х
t
2 3
уравнение примет вид :
1
t 4,
t
t
t 2 4t 1 0, D 16 4 12
t1
4 2 3
2 3
2
t2
4 2 3
2 3
2
16. Показательные уравнения. Примеры
+Показательные уравнения.
Примеры
=4
Пример 11 (скрытая замена переменной)
Вернемся к исходной переменной :
х
2 3 2 3
х
1
2 3
2 3
2 3 2 3
x
2
x
1
2
x 2
1
или
х
2 3 2 3
2 3
x
1
2
x 2
Ответ : 2; 2.
x
2
2 3
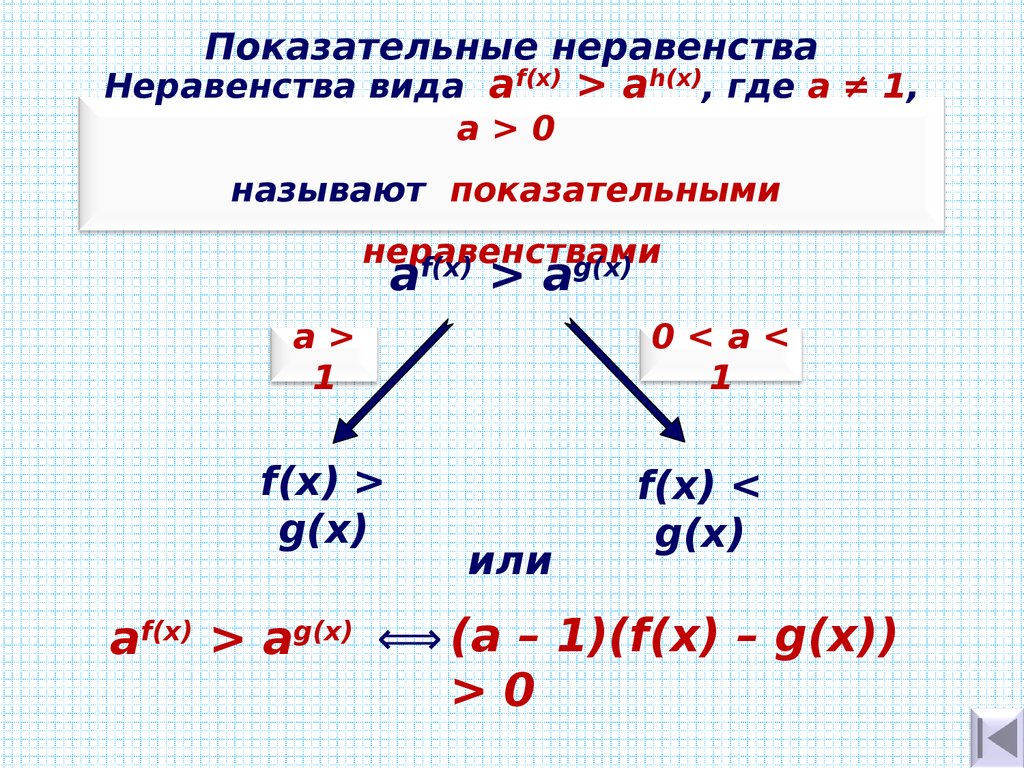
17. Показательные неравенства
Неравенства вида af(x) > аh(х), где а ≠ 1,a>0
называют показательными
неравенствами
f(x)
g(х)
a
>а
а>
1
f(x) >
g(х)
0<а<
1
или
f(x) <
g(х)
af(x) > аg(х) ⟺ (а – 1)(f(x) – g(x))
>0
18. Показательные неравенства. Примеры
Пример 122 x 4 64
22 x 4 26
т.к . функция у 2t монотонно
возрастает на R , то
2x 4 6
x 5
Ответ : 5;
Пример 2
1
3
2 x 3 ,5
1
3
2 x 3 ,5
1
3
1
3
0 ,5
t
1
т.к . функция у
3
монотонно убывает на R , то
2x 3 ,5 0 ,5
x 2
Ответ : 2;
19. Показательные неравенства. Примеры
Пример 30,5
x 2 3 x
0,53 x 8
т.к . функция у 0,5 t
монотонно убывает на R , то
x 2 3 x 3x 8
x 2 6x 8 0
н .ф. : x 2 6x 8 0
x1 2,
x 4
+
2
2
х ; 2 4;
Ответ : ; 2 4;
+
−
4
х
20. Показательные неравенства. Примеры
Пример 48 x 18 х 2 27 x
23 x 2х 32x 2 33 x
: 33 х , т.к . 33 х 0
23 x 2х 32x 2 33 x
3х
3х
3
3
33 х
2
3
3x
x
2
2
3
x
2
Пусть t , где t 0
3
t3 t 2 0
t 3 t 2 t 3 t 1 1 t 3 1 t 1 t 1 t 2 t 2
т.к . t 2 t 2 0 для любых t , то t 1 0
t 1
21. Показательные неравенства. Примеры
Пример 4Вернемся к исходной переменной :
x
2
1
3
x
0
2
2
,
3
3
x
т.к . а
2
2
1, то ф ция у убывает на R
3
3
x 0
Ответ : ; 0 .

















 Математика
Математика