Формула квадрат суммы двух выражений:

1. Устная работа

• Найти квадраты выражений y; 4; 3m; 8xy; 5a2b.
Как можно назвать эти выражения?
• Найти произведение одночленов 6x и 3y
Чему равно их удвоенное произведение?
• Прочитать выражение:
a) m + n
б) (m+n)2
в) m2+n2
г) 2mn
д) (m-n)2
е) m2 - n2
• Выполнить умножение многочленов (а+в)(а+в).
Как можно назвать полученное выражение?

2.

ФОРМУЛА
КВАДРАТ СУММЫ ДВУХ
ВЫРАЖЕНИЙ:
(а +
2
b) =
2
а
+ 2аb +
2
b

3. ПРИМЕНЕНИЕ ФОРМУЛЫ КВАДРАТА СУММЫ (а + b)2 = а2 + 2аb + b2

Вместо a и b в эту формулу можно подставить любые
выражения

4. Остров исследований

Результат умножения
1) (m + n) (m + n) =
=
2) (c + d) (c + d) =
=
3) (p + q) (p + q) =
=
4) (k + 3) (k + 3) =
=
5) ( 5 + m)( 5 + m) =
=

5. Остров исследований

Результат умножения
1) (m + n) (m + n) =
= m2 + 2 m n + n2
2) (c + d) (c + d) =
= c2 + 2 c d + d2
3) (p + q) (p + q) =
= p2 + 2qp + q2
4) (k + 3) (k + 3) =
= k2 + 6 k + 9
5) ( 5 + m)( 5 + m) =
= n2 + 10 n + 25

6. Остров исследований

1) (m + n) (m + n) =
(m + n)2
= m2 + 2 m n + n2
2) (c + d) (c + d) =
(c + d) 2
= c2 + 2 c d + d2
3) (p + q) (p + q) =
(p + q)2
= p2 + 2qp + q2
4) (k + 3) (k + 3) =
(k + 9)2
= k2 + 6 k + 9
5) ( 5 + m)( 5 + m) =
( 5 + m)2
= n2 + 10 n + 25

7. Остров исследований

Результат умножения
1) (m - n) (m - n) =
=
2) (c - d) (c - d) =
=
3) (p - q) (p - q) =
=
4) (k - 3) (k - 3) =
=
5) ( 5 - m)( 5 - m) =
=

8. Остров исследований

Результат умножения
1) (m - n) (m - n) =
= m2 - 2 m n + n2
2) (c - d) (c - d) =
= c2 - 2 c d + d2
3) (p - q) (p - q) =
= p2 - 2qp + q2
4) (k - 3) (k - 3) =
= k2 - 6 k + 9
5) ( 5 - m)( 5 - m) =
= n2 - 10 n + 25

9. Остров исследований

1) (m - n) (m - n) =
(m - n)2
= m2 - 2 m n + n2
2) (c - d) (c - d) =
(c - d) 2
= c2 - 2 c d + d2
3) (p - q) (p - q) =
(p - q)2
= p2 - 2qp + q2
4) (k - 3) (k - 3) =
(k - 9)2
= k2 - 6 k + 9
5) ( 5 - m)( 5 - m) =
( 5 - m)2
= n2 - 10 n + 25

10.

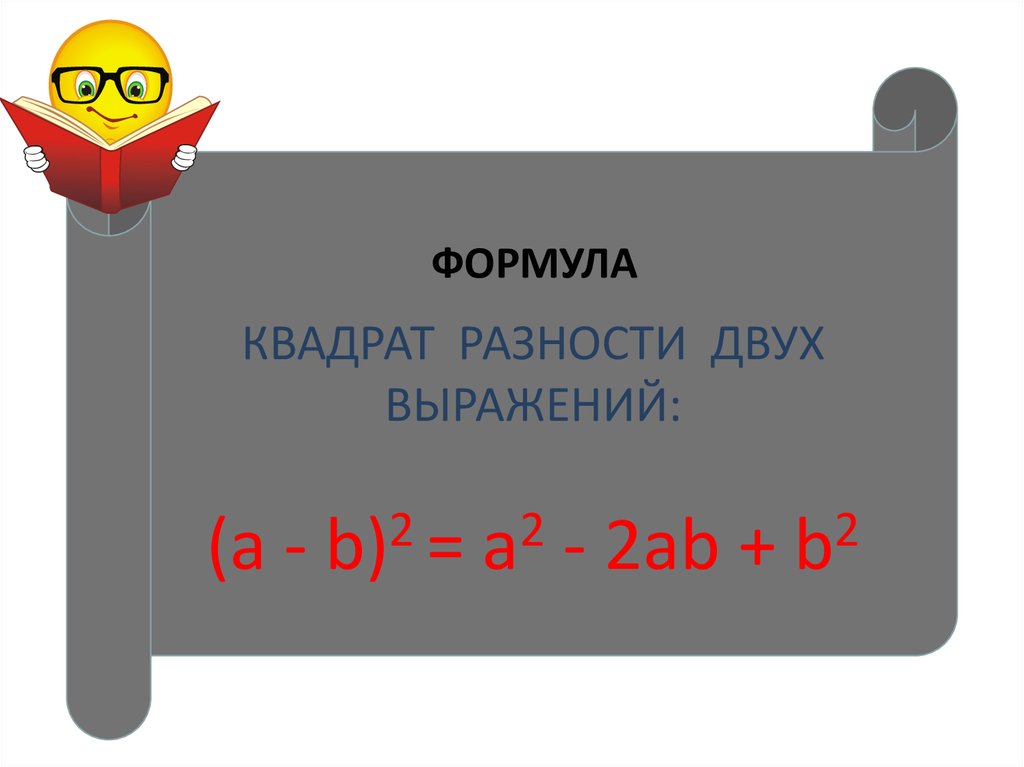
ФОРМУЛА
КВАДРАТ РАЗНОСТИ ДВУХ
ВЫРАЖЕНИЙ:
(а -
2
b) =
2
а
- 2аb +
2
b

11. ПРИМЕНЕНИЕ ФОРМУЛЫ КВАДРАТА РАЗНОСТИ (а - b)2 = а2 - 2аb + b2

ШИФРОГРАММЫ:

12. НАЙДИ ОШИБКИ:

2
у)
2
2
у
(b = b – 2bу +
2
2
(6 + с) = 36 -+12с + с
2
2
(р - 10) = р - 20р + 10 0
2
2
4 +1
(2а + 1) = 4а + 2а

13.

Геометрическая интерпретация
Дневнегреческий ученый Евклид доказывал формулы
квадрата суммы и квадрата разности геометрически.
Пользуясь рисунками, восстановите его
доказательство.

14.

Геометрический смысл формулы
(а + b)² = а² + 2аb + b²
геометрический смысл выражения (а+в) ²
- Чему равна площадь полученного квадрата?

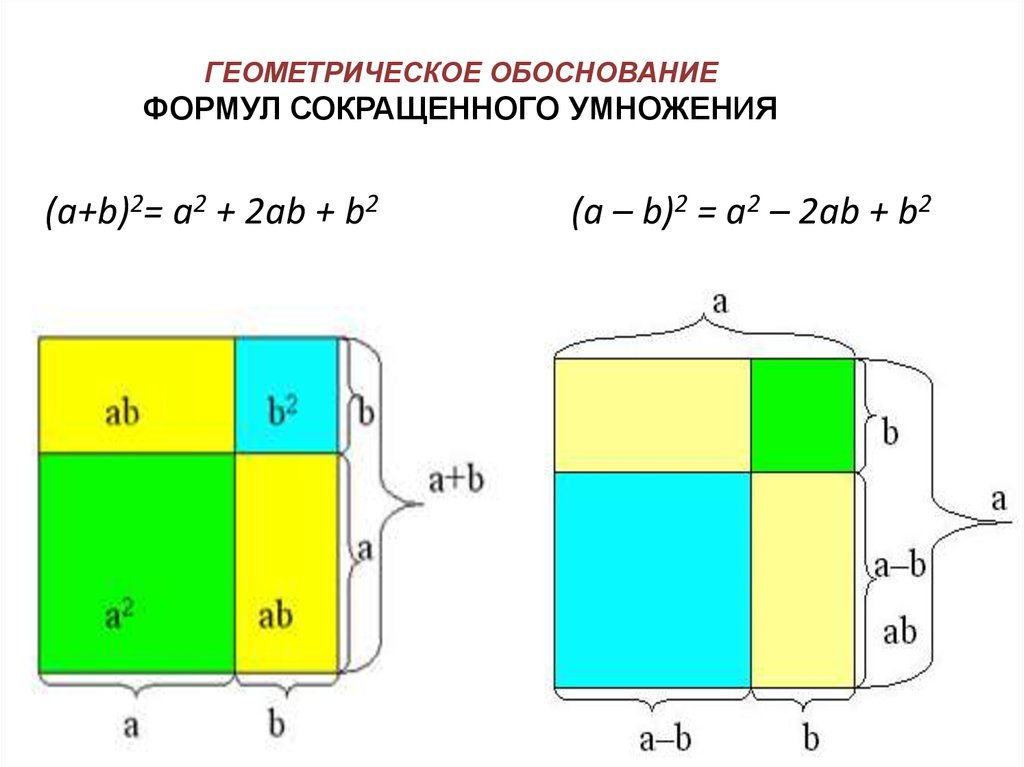
15. ГЕОМЕТРИЧЕСКОЕ ОБОСНОВАНИЕ ФОРМУЛ СОКРАЩЕННОГО УМНОЖЕНИЯ

(a+b)2= a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2

16.

Квадрат суммы нескольких выражений равен
сумме квадратов этих выражений плюс
удвоенные произведения каждого из них на
каждое последующее
• (a + b + c)² = a² + b² + c² + 2ab + 2ac +2bc
• (a + b + c + d) ² = a² + b² + c² + d² + 2ab +
+2ac + 2ad + 2bc + 2bd + 2cd

17.

Представить в виде многочлена:
f 2 fd d
2
1) f d
2
m 2m 1
2
2) m 1
2
9k 24k 16
2
3) 3k 4
2
4) 2 x 7 y
2
6) b d
7) 5 p 4q
5) c k
2 2
3 2
2
3
4 2
2
4 x 28 xy 49 y
4
c 2ck k
2
2
4
b 2b d d
4
2
3
2
6
25 p 40 p q 16q
6
3
4
8

18.

Представить в виде многочлена:
1) s z
2
2) m 1
2
3) 4 3k
2
4) 5 x 2 y
2
6) t c
7) 3m 4n
2
5) k p
2
7 2
4
6
3 2
s 2 sz z
2
2
m 2m 1
2
16 24k 9k
2
25 x 20 xy 4 y
2
k 2k p p
4
2
2
2
t 2t c c
8
4 7
14
9m 24m n 16n
12
6
3
6