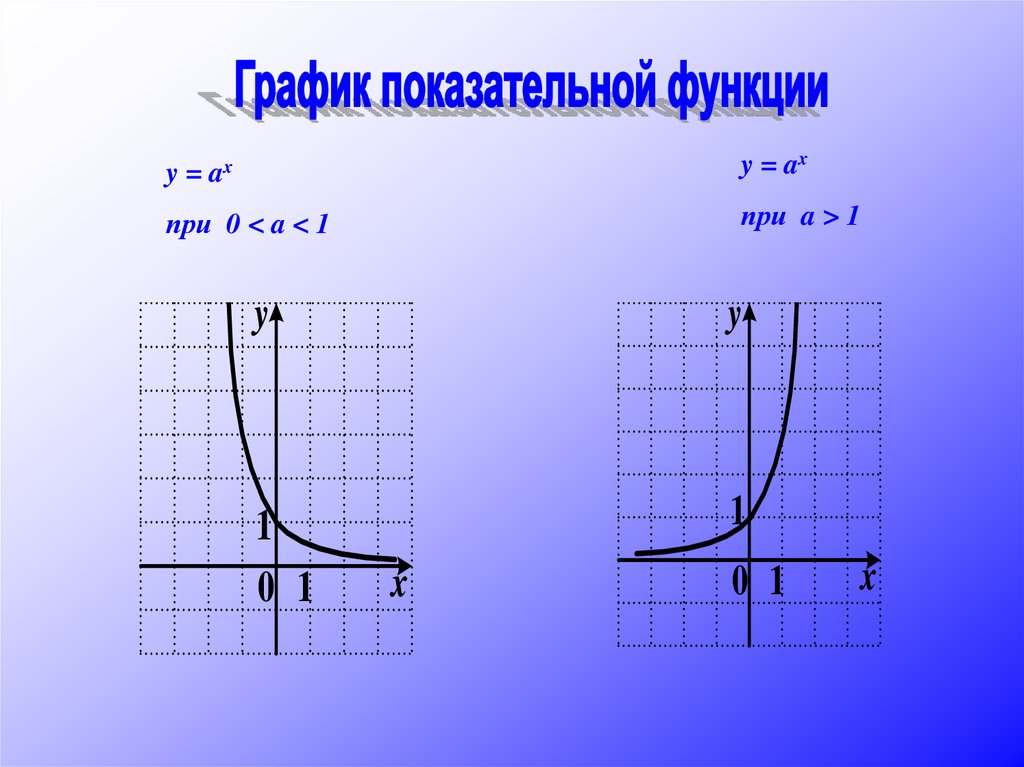
График показательной функции

1.

2.

Какую функцию
называют
показательной?
Показательной
функцией
называется
функция y=ax,
где х-переменная,
a-заданное число,
a>0, a≠1.

3.

Перечислите
основные свойства
показательной
функции?
Показательная функция обладает
следующими свойствами:
Област ь определения функции –
множест во R всех дейст вит ельных
чисел.
Множест во значений функции –
множест во всех положит ельных
чисел.
Показат ельная функция y=ax
являет ся возраст ающей на множест ве
всех дейст вит ельных чисел, если
a>1, и убывающей, если 0<a<1.

4.

y = ax
y = ax
при 0 < a < 1
при a > 1
y
y
1
0 1
1
x
0 1
x

5.

Основные свойства степени
с действительным показателем
Если a>0, b>0, x, x1 и x2 - любые действительные
числа, то справедливы следующие свойства:
a
a
x1
a
x1 x2
x2
a
a
x1 x2
x1 x2
,
ab x
,
x
a xb x ,
a x 0,
ax
a
x,
b
b
a x 1, если
a x1
x1 x2
a
,
x2
a
a 1, x 0,
a x1 a x2 , если
a 1, x1 x2 ,
a x1 a x2 , если
0 a 1, x1 x2 .

6.

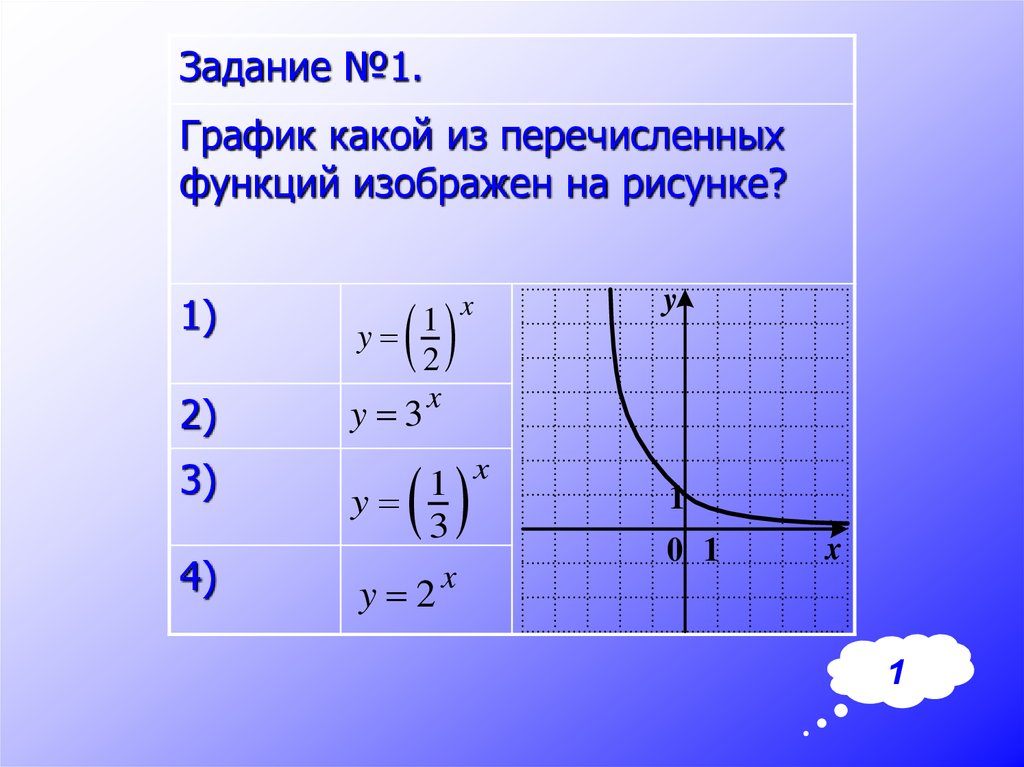
Задание №1.
График какой из перечисленных
функций изображен на рисунке?
1)
x
y
1
y 1
2
x
2)
y 3
3)
x
1
y
3
4)
y 2
x
0 1
x
1

7.

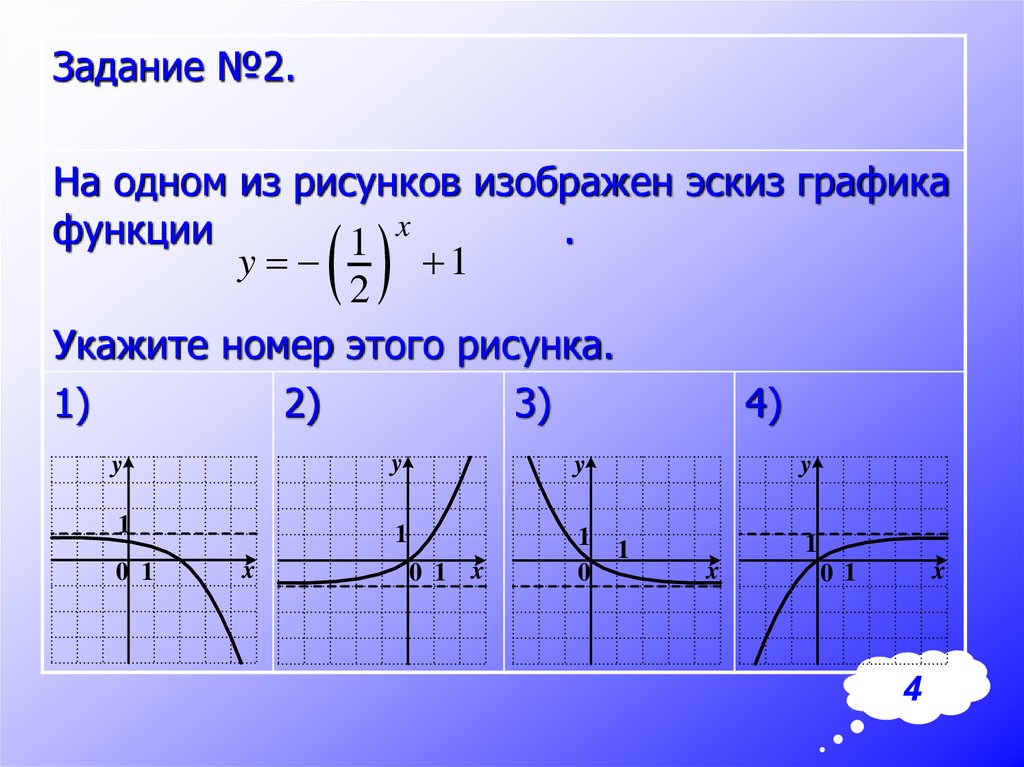
Задание №2.
На одном из рисунков изображен эскиз графика
x
функции
.
1
y
1
2
Укажите номер этого рисунка.
1)
2)
3)
4)
y
y
y
1
1
1
0
0 1
x
0 1 x
y
1
1
x
x
0 1
4

8.

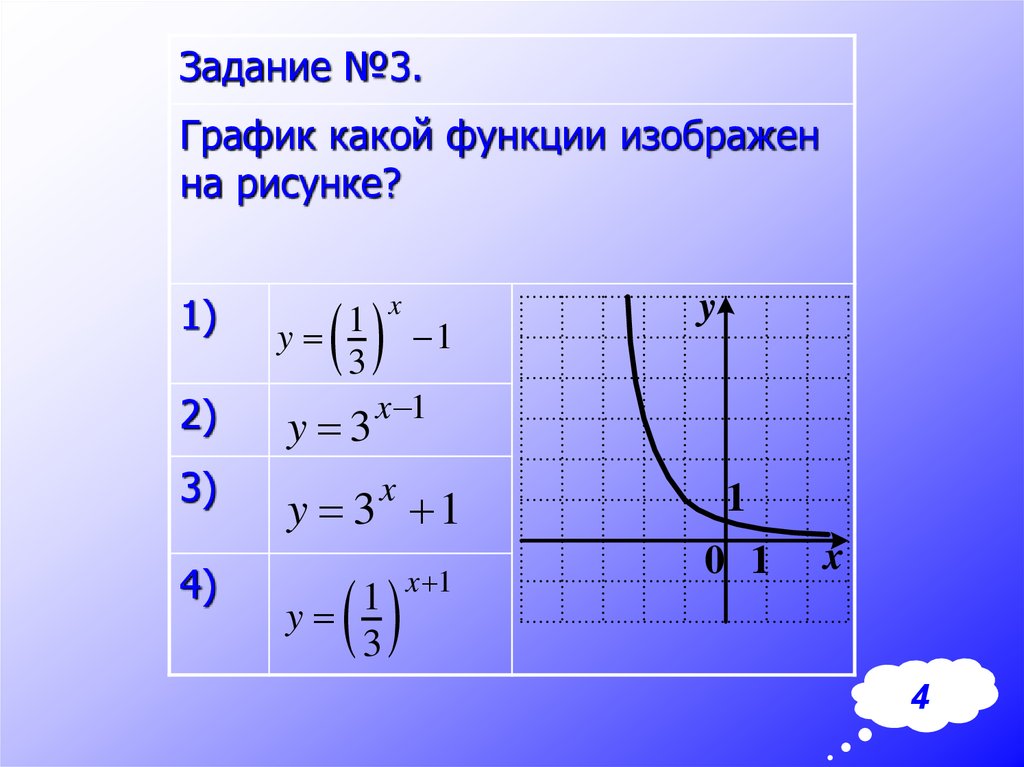
Задание №3.
График какой функции изображен
на рисунке?
1)
2)
3)
4)
y 1
3
x
y 3
x 1
1
x
y
y 3 1
1
0 1
y 1
3
x 1
x
4

9.

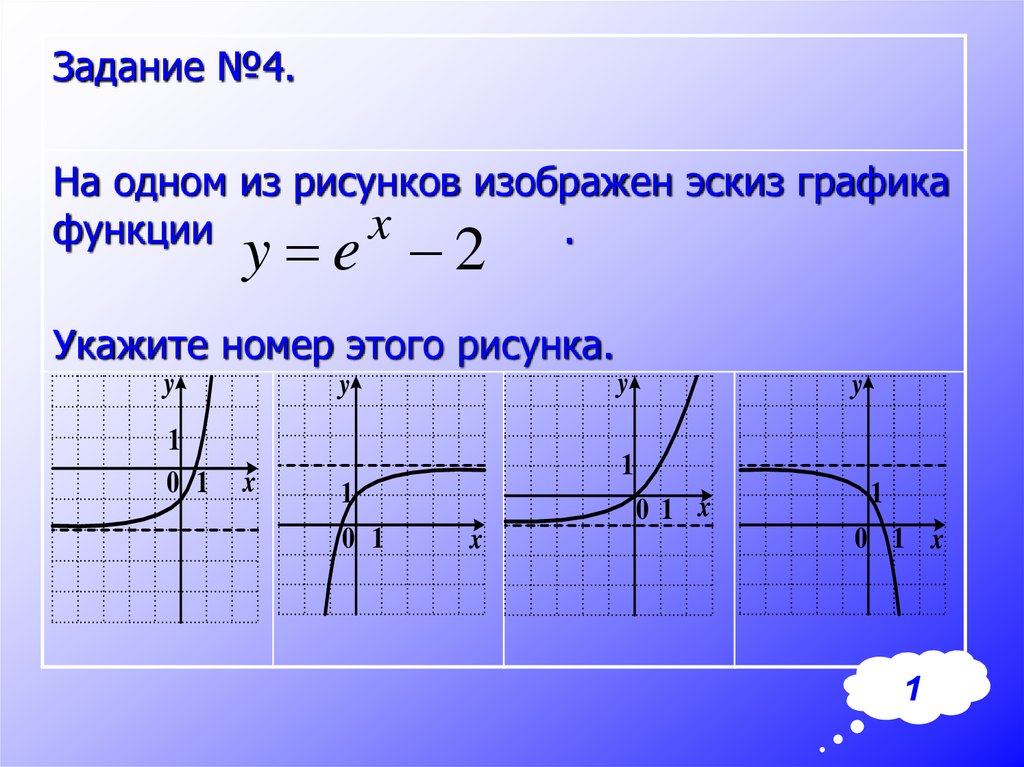
Задание №4.
На одном из рисунков изображен эскиз графика
x
функции
.
y e 2
Укажите номер этого рисунка.
y
1
0 1
y
y
x
y
1
1
0 1
0 1 x
x
1
0 1 x
1

10.

Задание №5.
Какое из следующих чисел входит в множество
значений функции ?
х
4
у 5
7
1) -9;
2) -7;
3) -5;
4) -3.
4

11.

Задание №6.
Укажите характер монотонности функции:
1)
1
у
7
Функция
убывае
т
х
2)
у 3
Функция
возрастает
х
3)
у 5
Функция
возрастает
х 2
4)
1
у
5
Функция
убывае
т
х 1

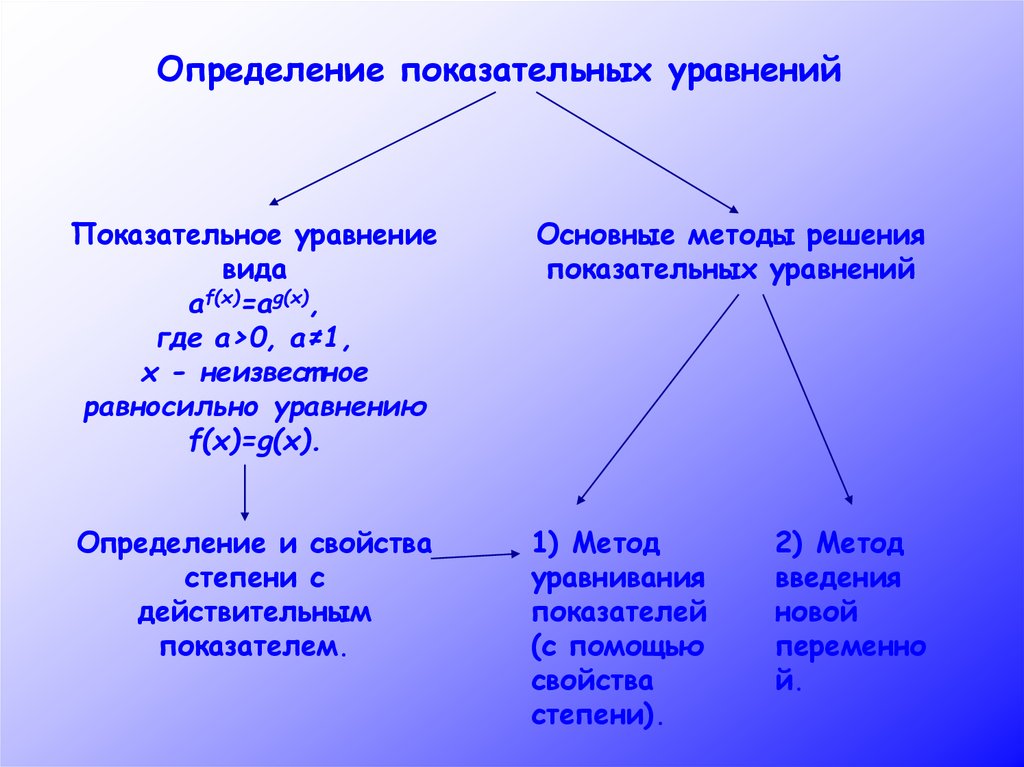
12.

Определение показательных уравнений
Показательное уравнение
вида
af(x)=ag(x),
где a>0, a≠1,
х - неизвест ное
равносильно уравнению
f(x)=g(x).
Основные методы решения
показательных уравнений
Определение и свойства
степени с
действительным
показателем.
1) Метод
уравнивания
показателей
(с помощью
свойства
степени).
2) Метод
введения
новой
переменно
й.

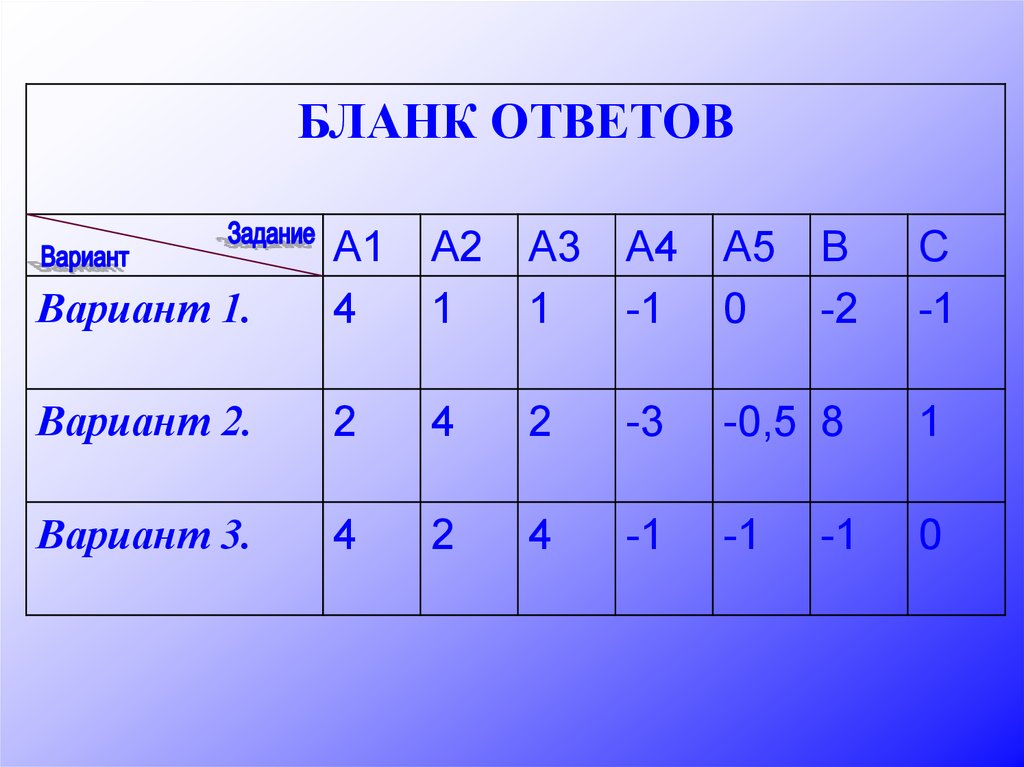
13.

БЛАНК ОТВЕТОВ
Вариант 1.
А1
4
А2
1
А3
1
А4
-1
А5
0
В
-2
Вариант 2.
2
4
2
-3
-0,5 8
1
Вариант 3.
4
2
4
-1
-1
0
-1
С
-1