Устные методы решения квадратных уравнений. Урок алгебры в 8 классе

1. Устные методы решения квадратных уравнений

Урок алгебры в 8 классе

2. СВОЙСТВА КОЭФФИЦИЕНТОВ

ax 2 bx c 0, a 0
Пусть дано квадратное уравнение
1. Если a b c 0 (сумма коэффициентов
x1 1, x2
равна нулю), то
2. Если
b . a c
.
c
a
, то x1 1, x2
.
c
a
Пример:
а) 4 x 2 13 x 9 0 , 4 – 13 + 9 =0, значит, x1 1, x2
9
4
б) 3 x 2 10 x 7 0 , 10 = 3 + 7, значит, x1 1, x2
7
3

3.

Решите уравнения:
1) 2x² + 3x + 1 = 0
2) 5x² – 4x – 9 = 0
3) 7x² + 2x – 5 = 0
4) х² + 17x – 18 = 0
5) 100x² – 97x – 197 = 0
6) 319х2 + 1988х + 1669 = 0
7) 313х2 + 326х + 13 = 0
8) 345х2 – 137х – 208 = 0
9) 339х2 + 378х + 39 = 0
10) 83х2 – 448х – 391 = 0;

4. Метод переброски

a b c 0 , то используют прием «переброски».
Пусть x1 и x2
- корни уравнения ax 2 bx c 0.
Если же
.
b
x1 x2 a
По теореме Виета
x x c
1 2 a
b
x1 x2 a
x x c
1 2 a
a
. Домножим первое уравнение
ax1 ax2 b
ax1 ax2 ac
2
a
на a , а второе на a 2
По теореме обратной
теореме Виета числа
y1 ax1, y2 ax2
являются корнями квадратного уравнения x 2 bx ac 0

5. Метод переброски

Таким образом, получаем следующий алгоритм
решения квадратного уравнения:
1. Если для коэффициентов уравнения ax 2 bx c 0
верно a b c 0, то составляем уравнение x 2 bx ac 0
(перебрасываем старший коэффициент).
2. По теореме обратной теореме Виета подбираем
корни уравнения y1, y2
3. Корнями исходного уравнения будут числа x1
y1
y
, x2 2
a
a
Пример:
2 x 2 11x 5 0
Перебрасываем старший коэффициент, получаем уравнение
x 2 11x 10 0 Его корни 10 и 1, делим их на 2.
1
Ответ: 5 ;
2

6.

Решите уравнения:
11) 4 x 2 24 x 32 0
12) 2 x 2 6 x 56 0
13) 2 x 13 x 24 0
2
14) 6 x 7 x 3 0
2
15) 4 x 17 x 15 0
2
16)
3 x 5 x 12 0
2

7.

8.

Группа А
3 x 10 x 3 0
2
6 x 37 x 6 0
2
4x 4 1 x 4 0
2
2
ax a 1 x a 0
2
2
x1 a
1
x2
a

9.

Группа В
2x 5x 2 0
2
3 x 10 x 3 0
2
4x 4 1 x 4 0
2
2
ax a 1 x a 0
2
2
x1 a
1
x2
a

10.

Группа С
3x 8 x 3 0
2
4 x 15 x 4 0
2
5x 5 1 x 5 0
2
2
ax a 1 x a 0
2
2
x1 a
1
x2
a

11.

Группа D
3x 8 x 3 0
2
4 x 15 x 4 0
2
5x 5 1 x 5 0
2
2
ax a 1 x a 0
2
2
x1 a
1
x2
a

12.

1) 11x 122 x 11 0
2
2) 9 x 82 x 9 0
2
3) 7 x 48 x 7 0
2
4) 5 x 24 x 5 0
2
5) 12 x 145 x 12 0
2
6) 12 x 2 143 x 12 0
7) 10 x 2 99 x 10 0
8) 8 x 2 65 x 8 0

13.

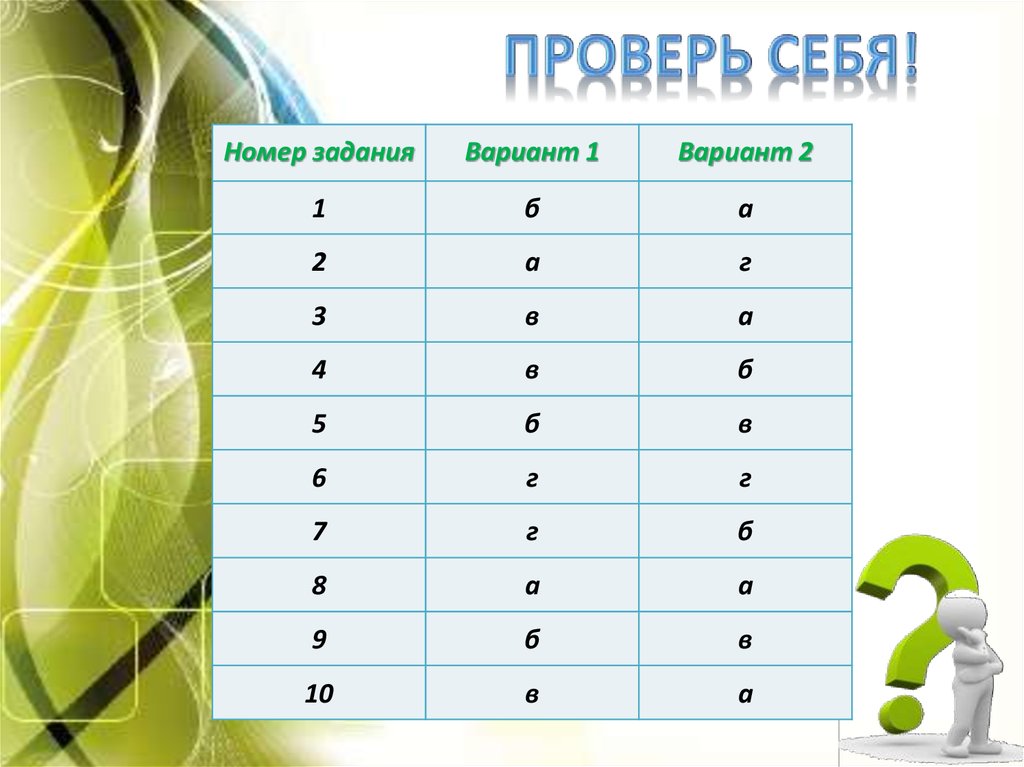
14.

Номер задания
Вариант 1
Вариант 2
1
б
а
2
а
г
3
в
а
4
в
б
5
б
в
6
г
г
7
г
б
8
а
а
9
б
в
10
в
а