Похожие презентации:
Координатная плоскость. 6 класс
1. МАОУ «Сладковская СОШ»
Координатная плоскость6 класс
Автор: Кайгородова С.В.
2. Цели урока:
• познакомить учащихся с понятием«Координатная плоскость», с историей
возникновения координат и координатной
плоскости;
• научить строить и находить координаты
точек;
• развивать абстрактное мышление; умения
сравнивать, выявлять закономерности;
• воспитывать ответственное отношение к
учебе; интерес к предмету.
3. Координаты в нашей жизни
Чтобы правильно занять свое место в кинотеатре, нужнознать две координаты – ряд и место.
4.
С помощью координатной сетки летчики, морякиопределяют местоположение объектов.
4
5.
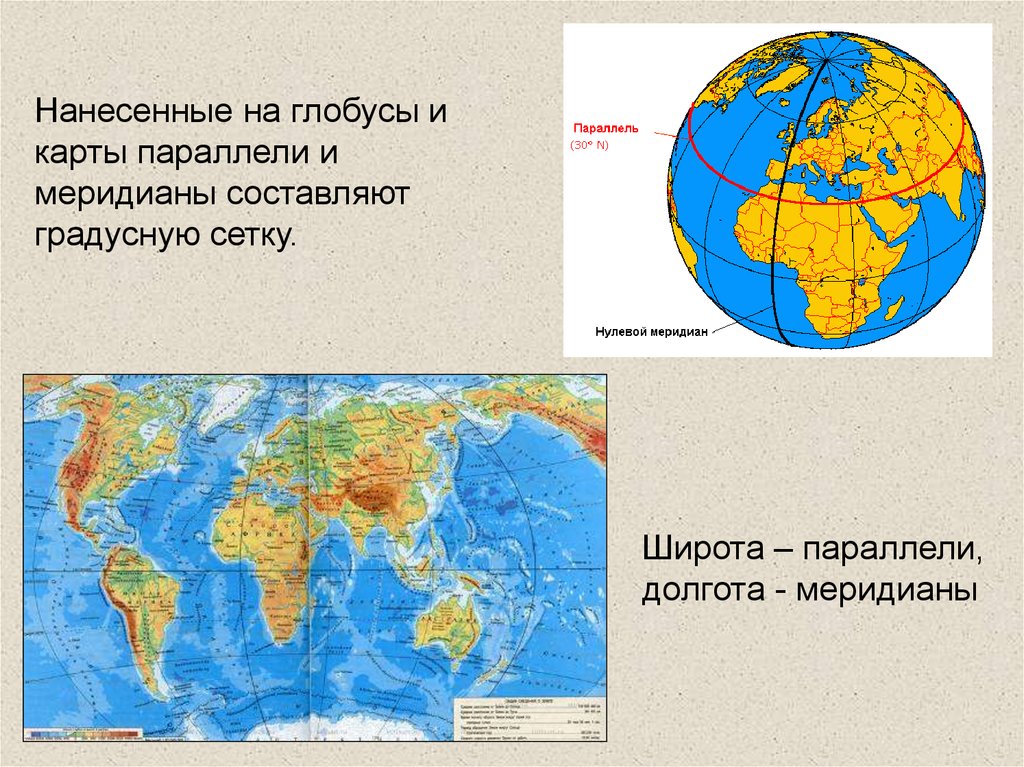
Нанесенные на глобусы икарты параллели и
меридианы составляют
градусную сетку.
Широта – параллели,
долгота - меридианы
6.
Вертикали – цифры,горизонтали – латинские
буквы.
Чтобы найти свое место в
поезде сначала мы ищем
свой вагон, затем номер
своего места.
7.
Историческая справкаИдея координат зародилась ещё в древности.
Первоначальное их применение связано с астрономией
и географией, с потребностью определить положение
светил на небе и объектов на поверхности Земли.
• Уже во II в. древнегреческий астроном Клавдий
Птоломей пользовался широтой и долготой в качестве
координат.
• Более чем за 100 лет до нашей эры греческий ученый
Гиппарх предложил провести на карте Земли параллели
и меридианы.
8.
• В ХIV веке французский ученый Оресле поаналогии с географическими координатами
создал координатную плоскость. Он поместил на
плоскость прямоугольную сетку и назвал широтой
и долготой то, что сейчас мы называем абсциссой
и ординатой.
• Однако основная роль в создании метода
координат принадлежит французскому ученому
Рене Декарту (1596 –1650). Введенные на
плоскости координаты х, у называют
декартовыми.
Термины «абсцисса» и «ордината»
(образованные от латинских слов «отсекаемый» и
«упорядоченный») были введены в 70-80 гг. XVII в.
немецким математиком Вильгельмом Лейбницем.
Рене Декарт
Готфрид
Вильгельм
фон Лейбниц
9.
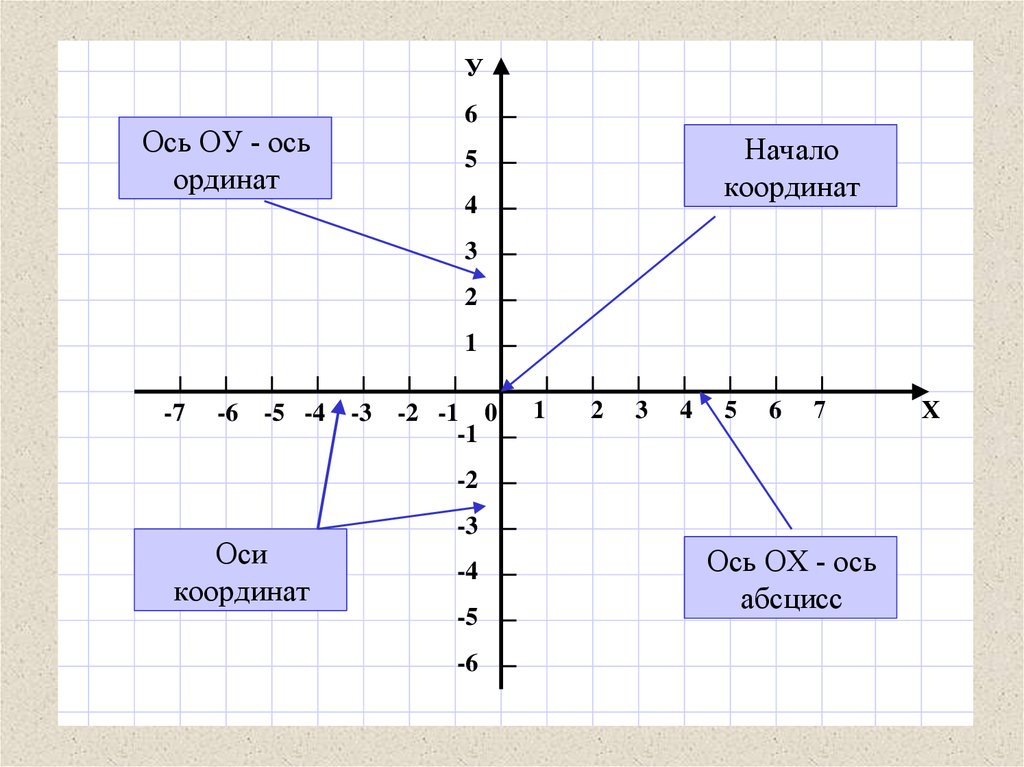
У6
Ось ОУ - ось
ординат
Начало
координат
5
4
3
2
1
-7
-6
-5 -4
-3
-2 -1 0
-1
1
2
3
4
5
6
7
-2
Оси
координат
-3
-4
-5
-6
Ось ОХ - ось
абсцисс
Х
10.
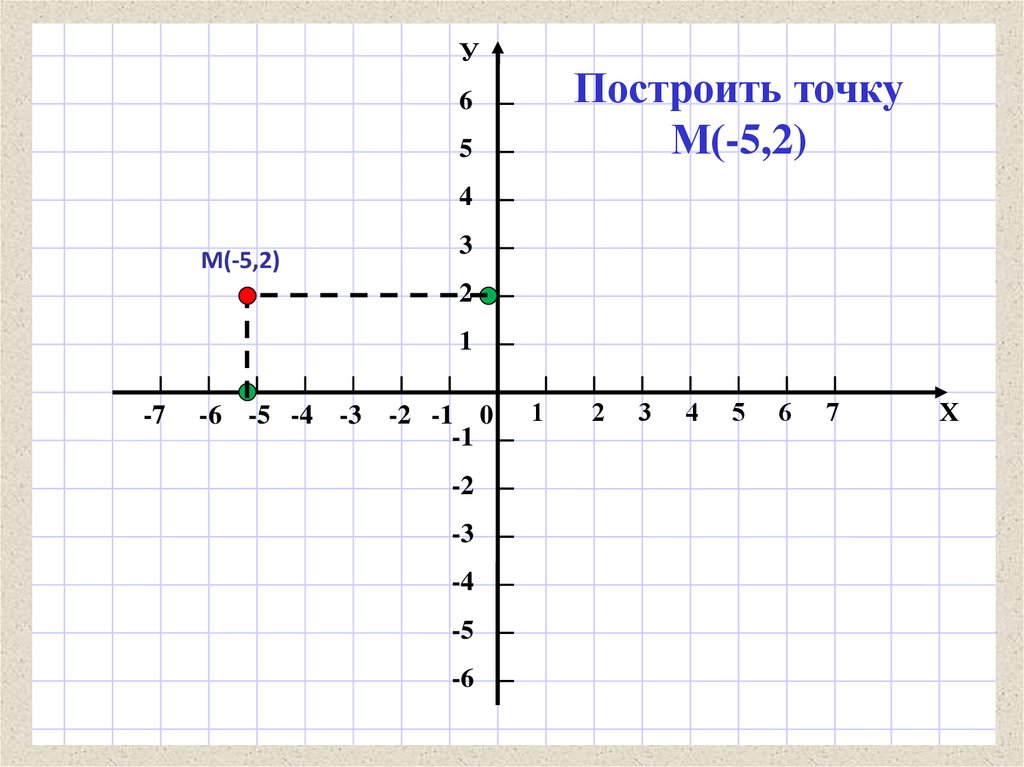
УПостроить точку
М(-5,2)
6
5
4
М(-5,2)
3
2
1
-7
-6
-5 -4 -3 -2 -1 0
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
7
Х
11.
В координатной плоскости xOy построить точки:A (-3; 1); B (-1; -2); C (-2: 4); D (2; 3); F (6: 4); K (4; 0)
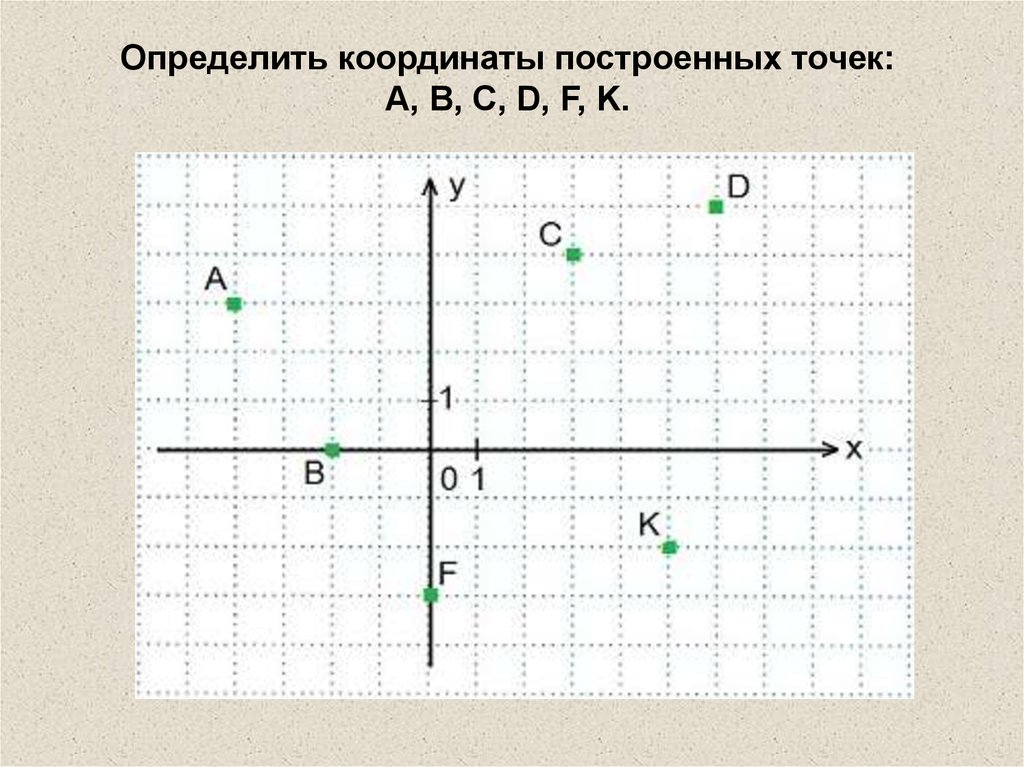
12. Определить координаты построенных точек: A, B, C, D, F, K.
13.
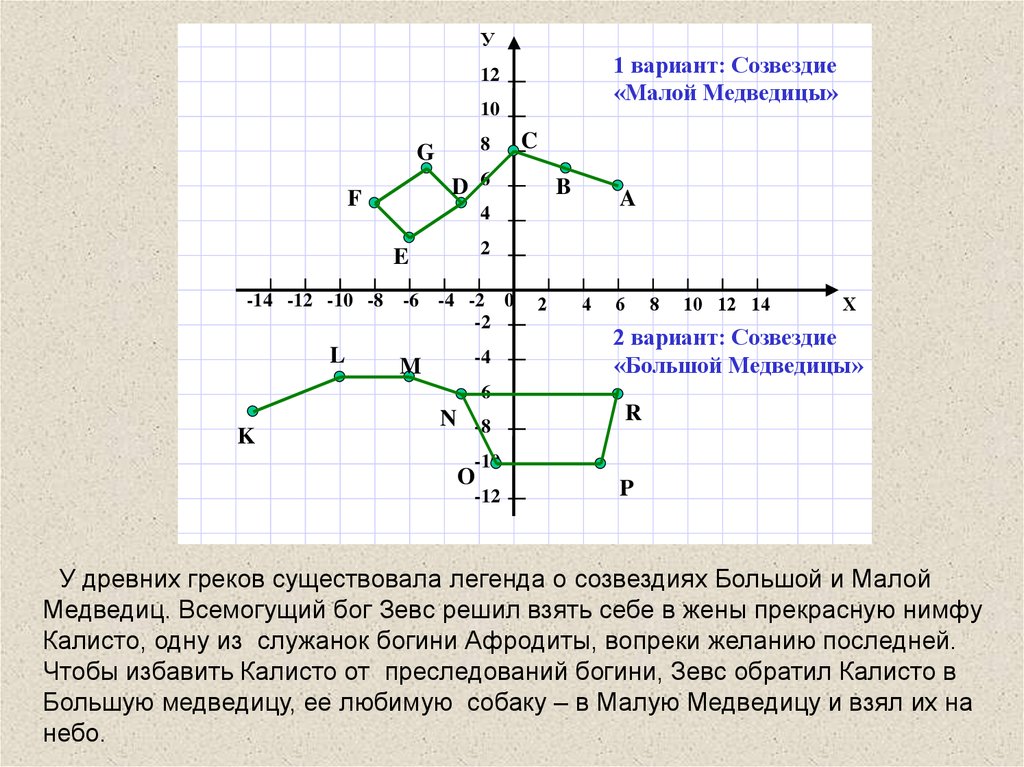
СозвездиеСозвездие
«Малой Медведицы»
«Большой Медведицы»
A(6;6),
B(3;7),
C(0;8),
D(-3;5),
E(-6;3),
F(-8;5),
G(-5;7),
D(-3,5).
K(-15;-7),
L(-10;-5),
M(-6;-5),
N(-3;-6),
O(-1;-10),
P(5;- 10),
R(6;-6),
N(-3;-6).
14.
У1 вариант: Созвездие
«Малой Медведицы»
12
10
8
G
D 6
F
L
B
A
4
2
E
-14 -12 -10 -8
C
-6
M
-4 -2 0
-2
-4
2
4
6
8
10 12 14
Х
2 вариант: Созвездие
«Большой Медведицы»
-6
K
N -8
R
-10
O
-12
P
У древних греков существовала легенда о созвездиях Большой и Малой
Медведиц. Всемогущий бог Зевс решил взять себе в жены прекрасную нимфу
Калисто, одну из служанок богини Афродиты, вопреки желанию последней.
Чтобы избавить Калисто от преследований богини, Зевс обратил Калисто в
Большую медведицу, ее любимую собаку – в Малую Медведицу и взял их на
небо.









 Математика
Математика








