Похожие презентации:
Угловой коэффициент прямой
1.
2. Угловой коэффициент прямой.
Прямая проходит через началокоординат и точку Р(3; -1).
Чему равен ее угловой
коэффициент?
k tg
у kх b
у kх
1 3k
1
k
3
3. Найдите угловые коэффициенты прямых:
k tg2
1
4
1
2
3
3
4
k 0,5
k 3
k 0
k 1
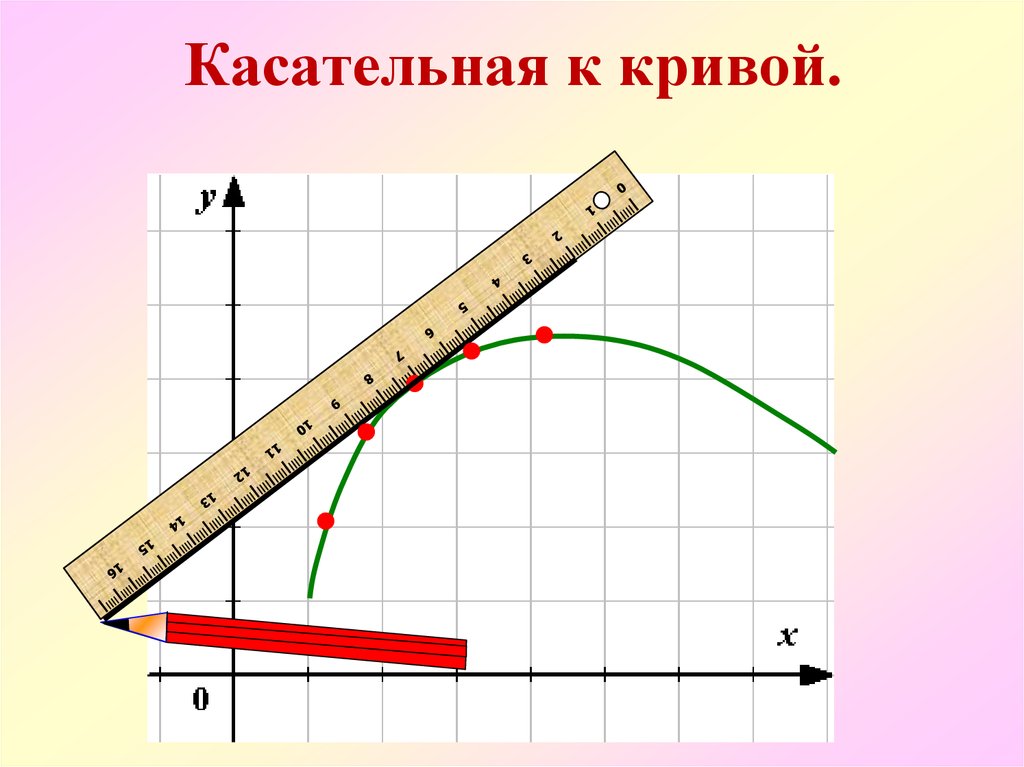
4. Касательная к кривой.
5.
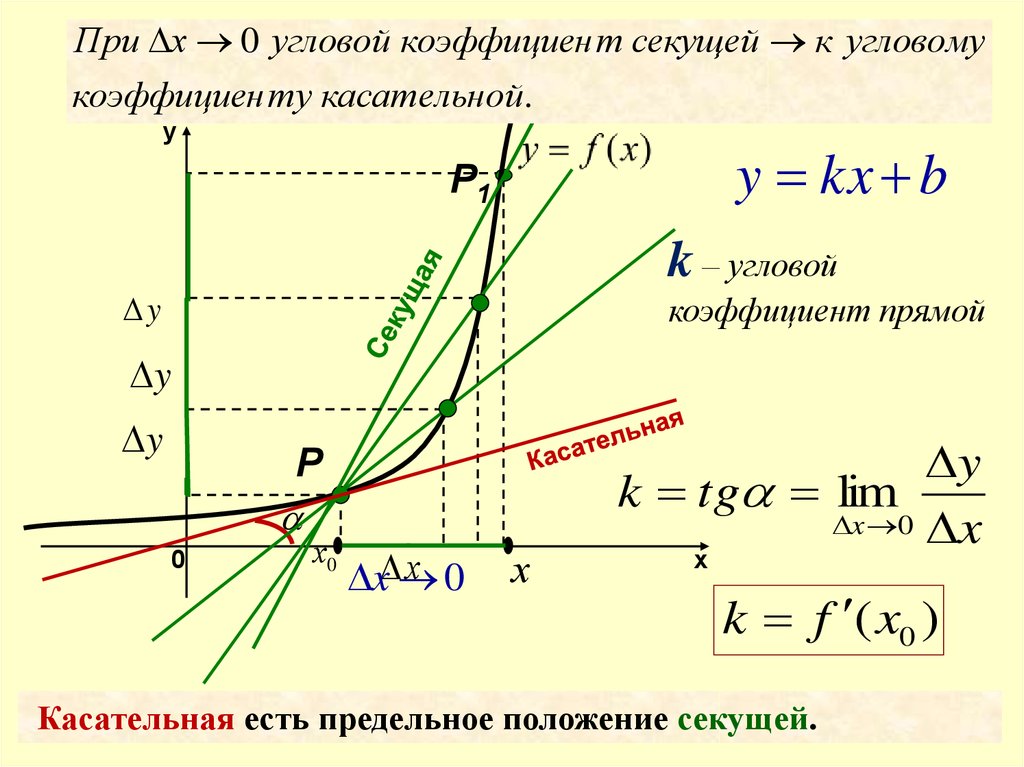
При х 0 угловой коэффициен т секущей к угловомукоэффициен ту касательной.
y
y kx b
Р1
k – угловой
y
коэффициент прямой
y
y
Р
0
х0
х 0
x
х
y
k tg lim
x 0 x
х
k f ( x0 )
Касательная есть предельное положение секущей.
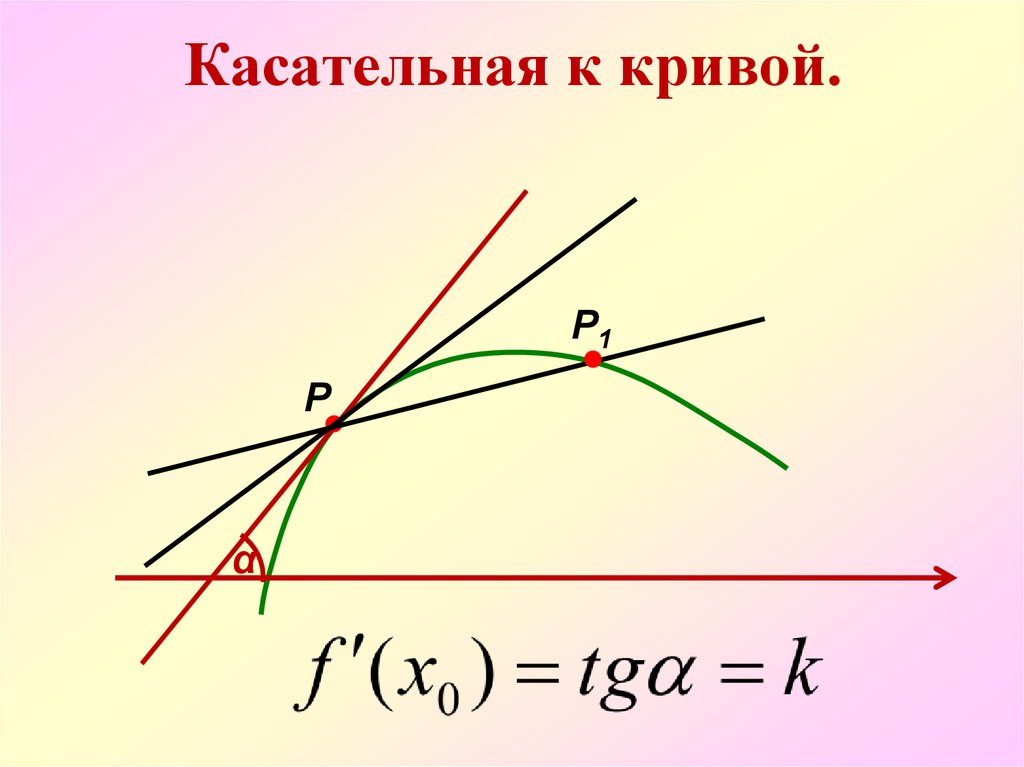
6. Касательная к кривой.
Р1Р
α
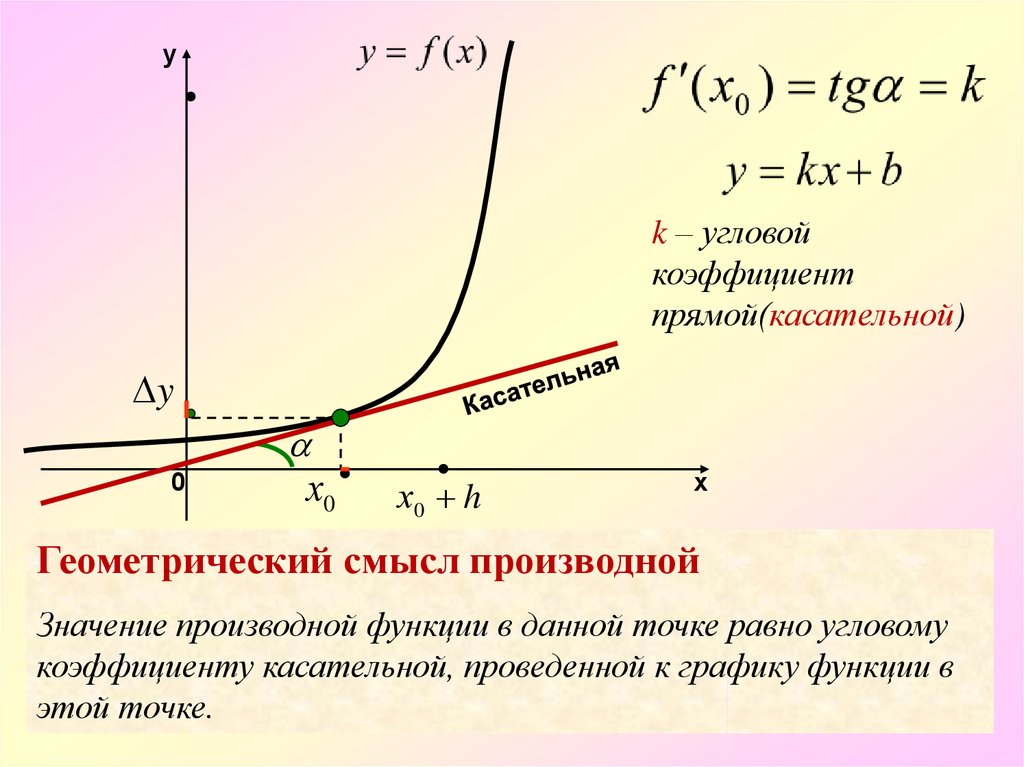
7.
yk – угловой
коэффициент
прямой(касательной)
y
0
х0
х0 h
х
Геометрический смысл производной
Значение производной функции в данной точке равно угловому
коэффициенту касательной, проведенной к графику функции в
этой точке.
8.
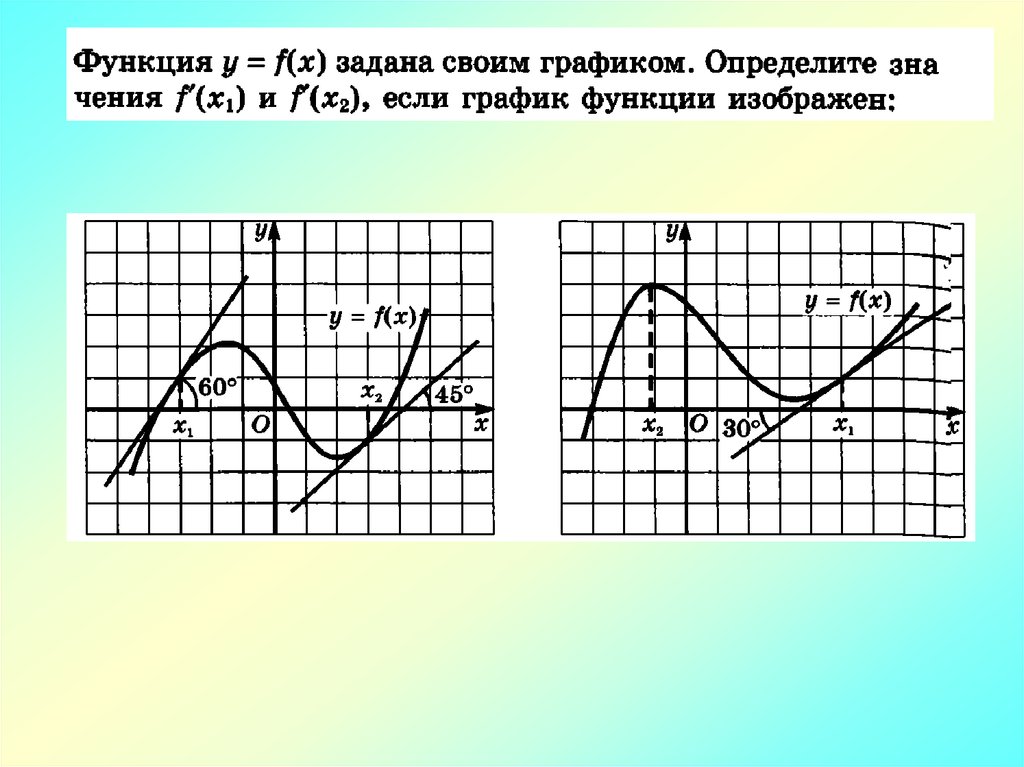
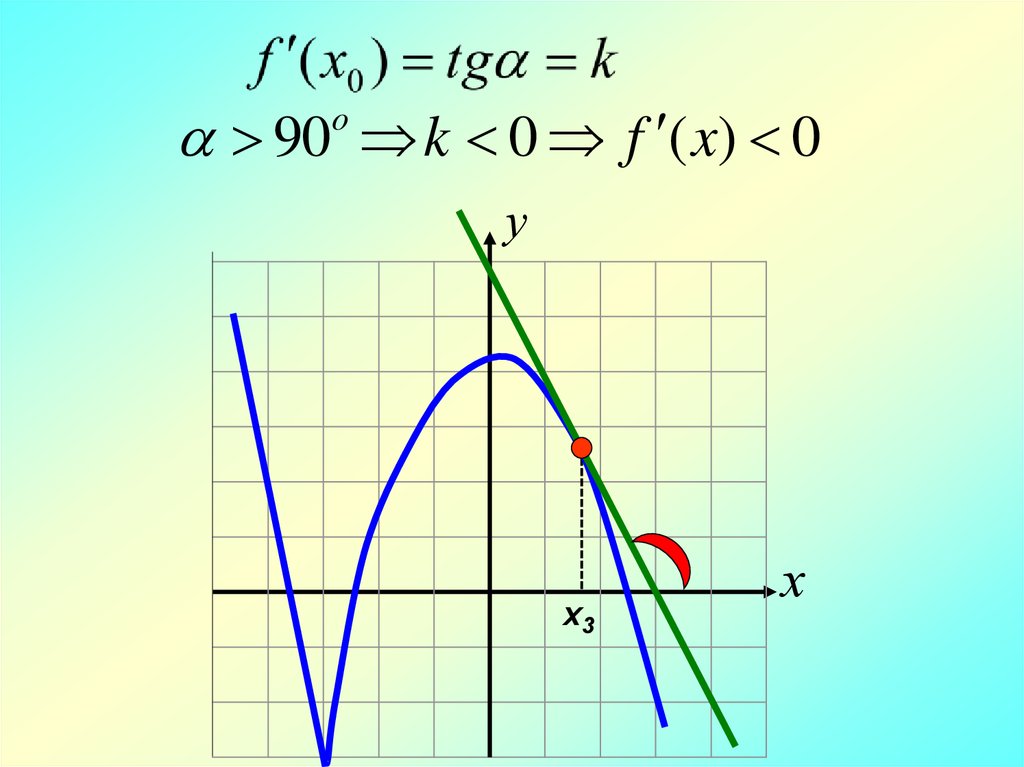
90 k 090 k 0
o
o
0 k 0, касательная параллельна ОХ
o
у
х1 х3
х2
х
9.
Нахождение производной.y
f ( x) lim
x 0 x
у f ( х х) f ( х)
f ( x) С
f ( x х) С
у С С 0
0
С lim
0
x 0 x
3 0
С 0
( 1,8) 0
10.
Нахождение производной.y
f ( x) lim
x 0 x
f ( x) х
f ( x х) х х
у х х х х
х
x lim
1
x 0 x
х 1
у f ( х х) f ( х)
11.
Нахождение производной.y
f ( x) lim
x 0 x
у f ( х х) f ( х)
f ( x) kх b
f ( x х) k ( х х) b kx k x b
у kх k х b kх b k х
k х
(kx b) lim
k
x 0 x
kx b k
3
3
х 7
4
4
5 х 5
12.
Нахождение производной.y
f ( x) lim
x 0 x
f ( x) х
у f ( х х) f ( х)
2
f ( x х) ( х х) 2 x 2 2 х x ( х) 2
у х 2 х х ( х) х 2 х х ( х)
2
2
2
2
х(2 х х)
х(2 х х)
( x ) lim
lim 2 x x 2 x
x 0
x 0
x
2
( х ) 2 х
2
13.
Нахождение производной.y
f ( x) lim
x 0 x
f ( x) х
у f ( х х) f ( х)
3
f ( x х) ( х х) x 3х x 3х( х) х
3
3
2
3
2
у x 3х x 3х( х) х х
3
2
3
2
3
3х х 3х х х х 3х 3х х ( х)
2
2
3
2
х 3х 3х х х
( x ) lim
x 0
x
3
2
( x ) 3х
3
2
2
3х
2
2
14.
С 0kx b k
х 1
( х ) 2 х
2
( x ) 3х
3
2
( x ) nх
n
n 1
15.
16.
ДЗ : 40, 5, 6;41, 1 3, 5 11
17.
С 0kx b k
х 1
( х ) 2 х
2
( x ) 3х
3
2
( x ) nх
n
n 1
18.
19.
20.
21.
22.
23.
Проверочная работа24.
25.
26.
Решение задач на касательную27.
28.
29.
30.
31.
32.
33. Повторение:
Линейныеуравнения
Алгебраическое
условие
y = к1х+b1
к1 = к2 , b1 ≠ b2
y = к2х+b2
к1 = к2, b1= b2
к1 ≠ к2
к1 ∙ к2 = -1
Геометрический
вывод
Прямые
параллельны
Прямые
совпадают
Прямые
пересекаются
Прямые
перпендикулярны
34.
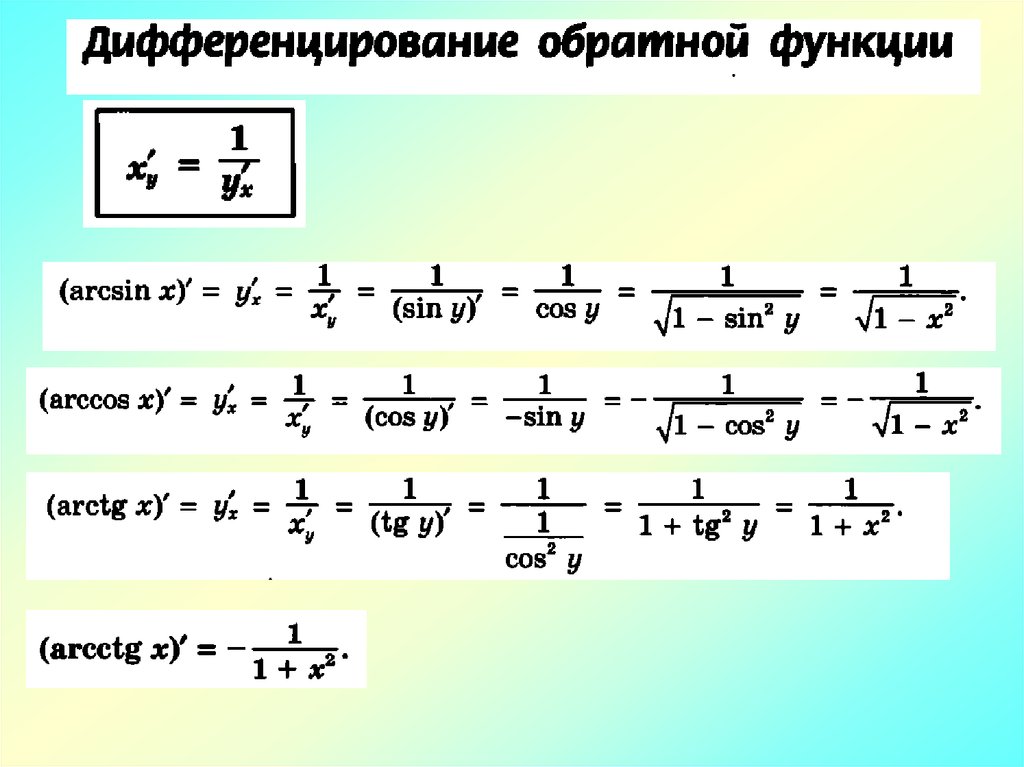
90 k 0 f ( x) 0o
у
х1
х
35.
0 k 0, касательная параллельна ОХo
у
х2
х
36.
90 k 0 f ( x) 0o
у
х3
х
37.
38.
39.
Теорема 1Пусть f ( x) дифференцируема на (а; b).
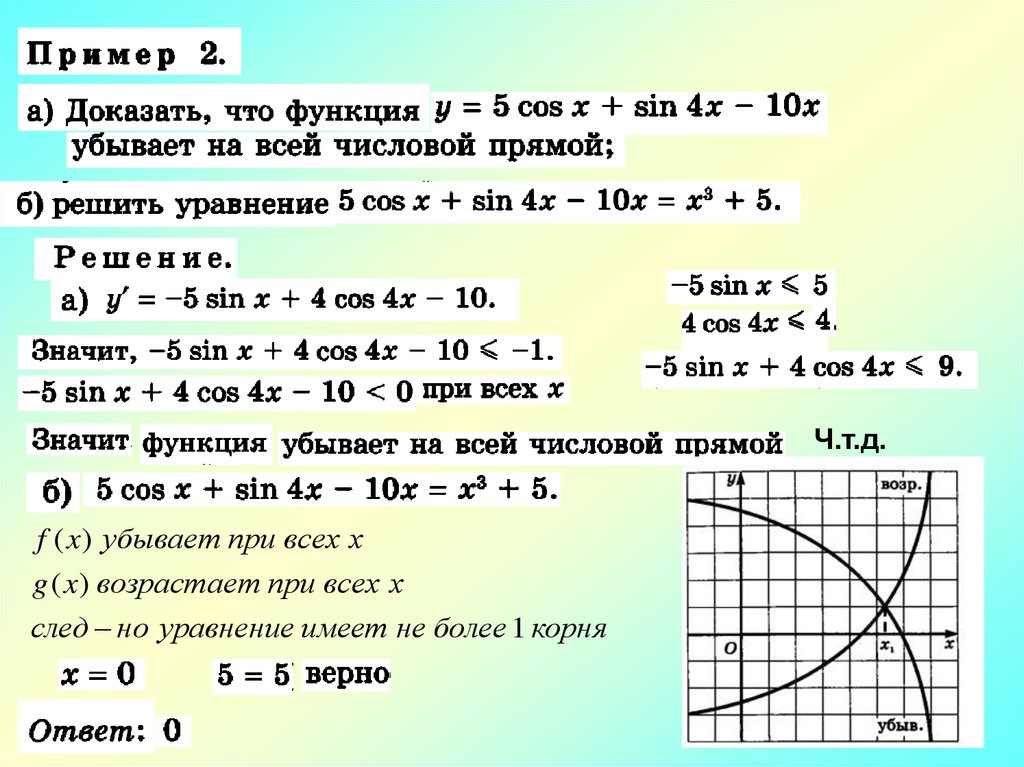
Если f ( x) 0 на (a; b), то f ( x) возрастает на (a; b).
Если f ( x) 0 на (a; b), то f ( x) убывает на (a; b).
40.
Ч.т.д.41.
Ч.т.д.f ( x) убывает при всех х
g ( x) возрастает при всех х
след но уравнение имеет не более 1 корня
42.
43.
Теорема 2 (условие постоянства функции)Пусть f ( x) дифференцируема на (а; b) и непрерывна на a; b .
Для того, чтобы непрерывная функция f ( x) была постоянна
на a; b необходимо и достаточно, чтобы f ( x) 0 на (a; b).
44.
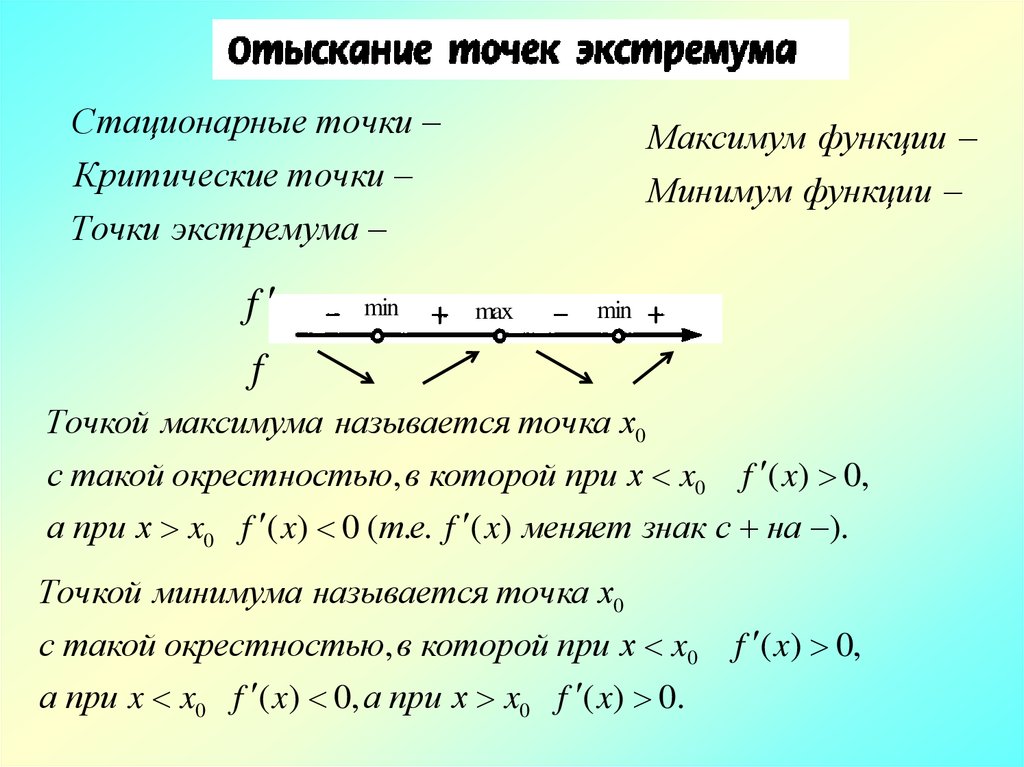
Стационарные точкиМаксимум функции
Критические точки
Минимум функции
Точки экстремума
f
min
max
min
f
Точкой максимума называется точка х0
с такой окрестностью, в которой при х x0 f ( x) 0,
а при х x0 f ( x) 0 (т.е. f ( x) меняет знак с на ).
Точкой минимума называется точка х0
с такой окрестностью, в которой при х x0
а при x x0 f ( x) 0, а при х x0 f ( x) 0.
f ( x) 0,
45.
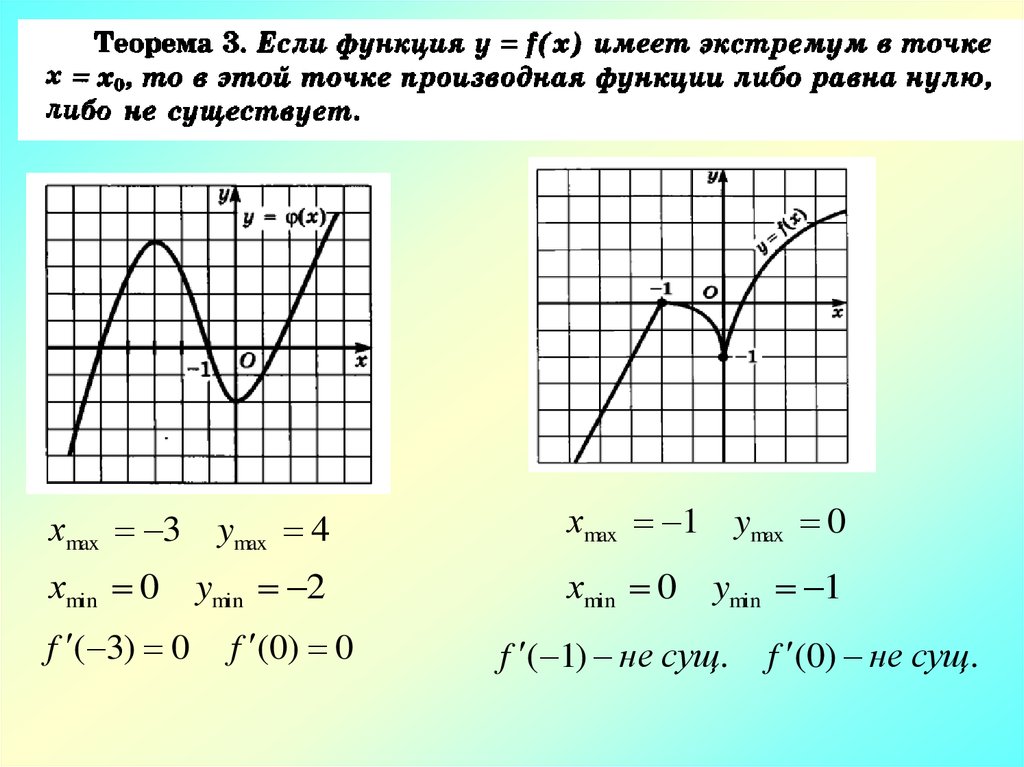
хmax 3 ymax 4хmax 1 ymax 0
хmin 0
хmin 0 ymin 1
f ( 3) 0
ymin 2
f (0) 0
f ( 1) не сущ.
f (0) не сущ.
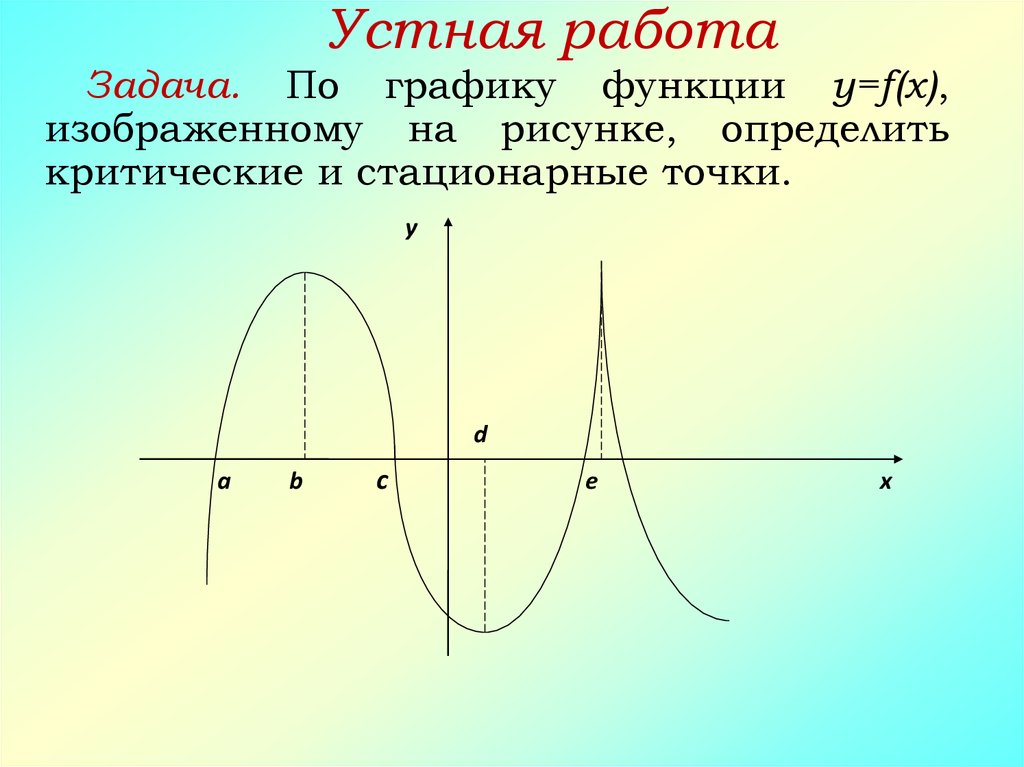
46. Устная работа
Задача. По графику функции y=f(x),изображенному на рисунке, определить
критические и стационарные точки.
y
d
а
b
c
e
x
47.
ff
х1 точка перегиба
х2 точка излома графика
х1
х2
48.
Теорема 4 (необходимое и достаточное условия экстремума)Для того, чтобы точка x0 была точкой экстремума f ( x) :
1)необходимо, чтобы х0 была стационарной или критической;
2)достаточно, чтобы при переходе через х0 f ( x) меняла знак.
Замечание
Если в точке x0 , где f ( x0 ) 0 не происходит смены знака ,
то точка х0 называется точкой перегиба.
49.
Алгоритм отыскания точек экстремума1)найти f ( x0 );
2)найти стационарные и критические точки;
3)определить знаки f ( x) на интервалах;
4)определить промежутки монотонности функции ;
5)определить точки экстремума , перегиба.
12 х ( х 2) 2 0
х 0
х 2
x min 0
min
f
f
хmin 0, х 2 точка перегиба
(не является экстремумом)
50.
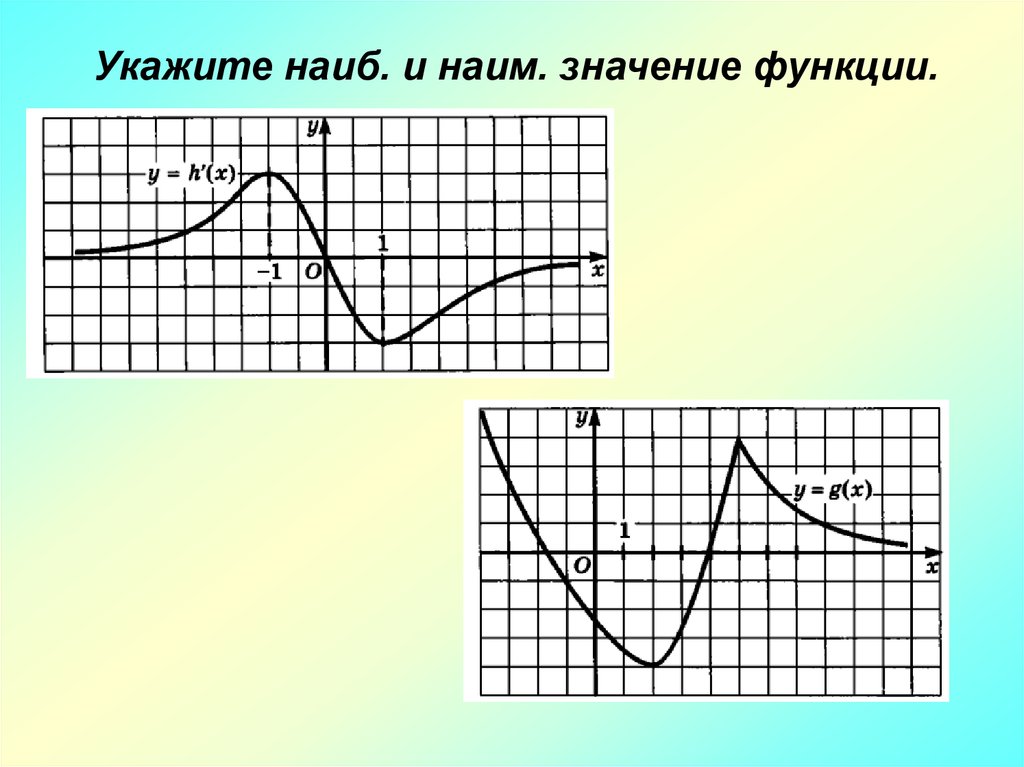
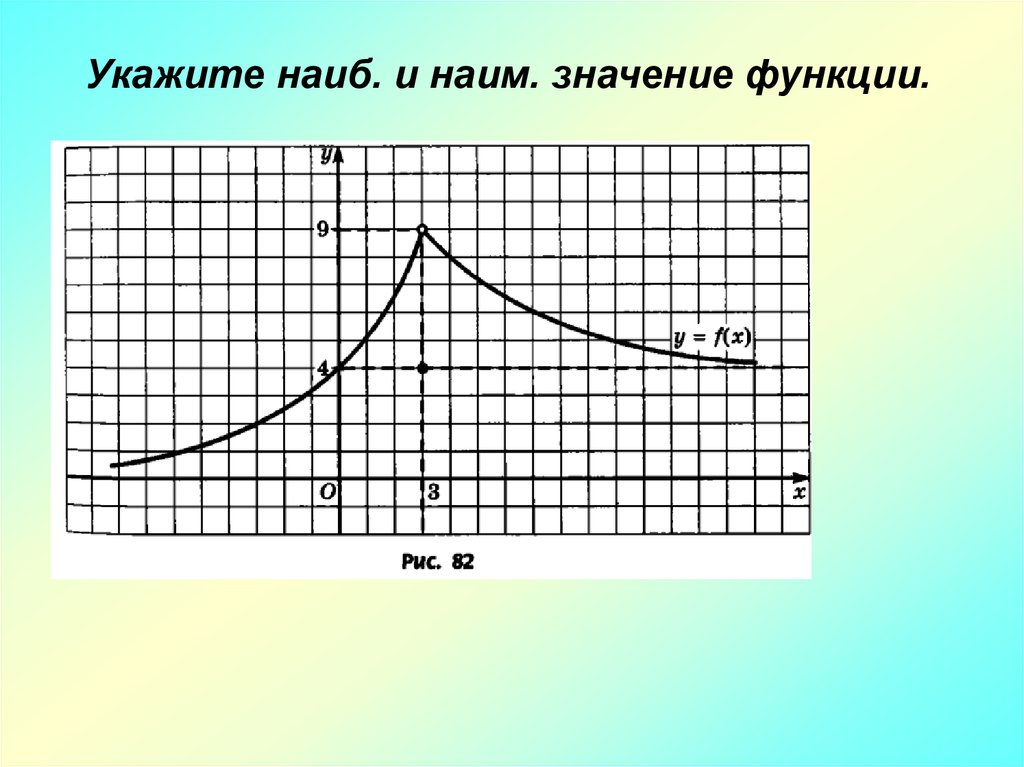
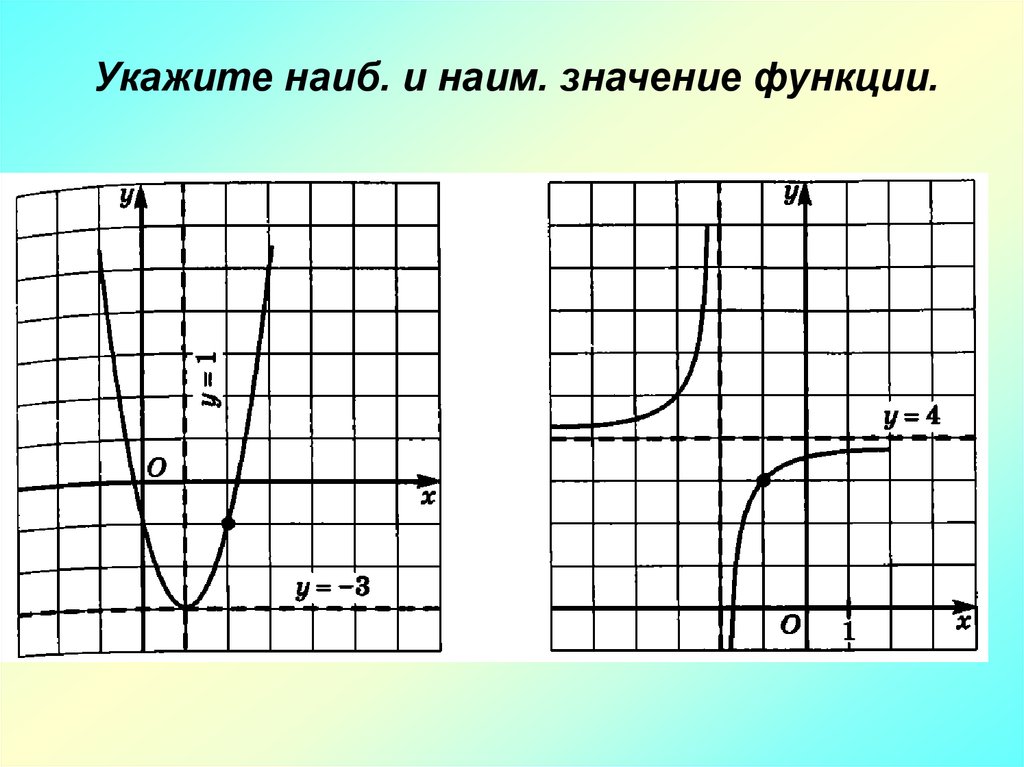
Алгоритм нахождения наибольшего инаименьшего значений функции на отрезке
1 )найти f ( x0 );
2 )найти стационарные и критические точки , лежащие
внутри отрезка ;
3 )вычислить значения f ( х ) на концах отрезка и в точках п.2 );
4 )выбрать среди этих значений у наиб или у наим .
2)
51.
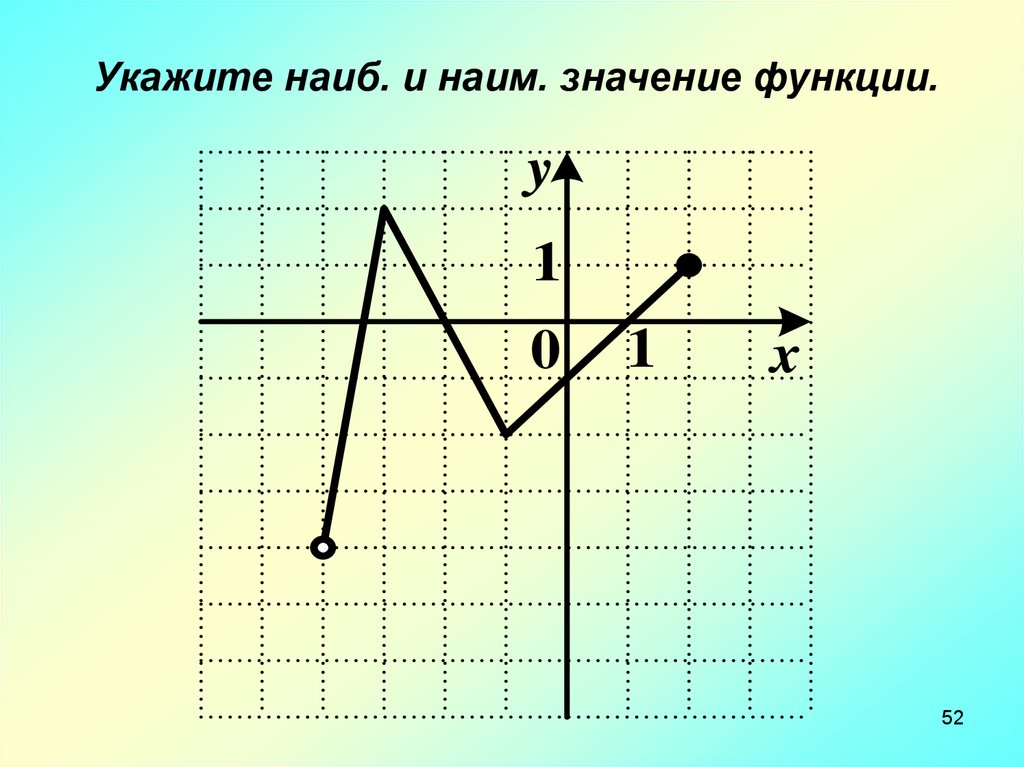
Укажите наиб. и наим. значение функции.y
1
01
x
51
52.
Укажите наиб. и наим. значение функции.y
1
0
1
x
52
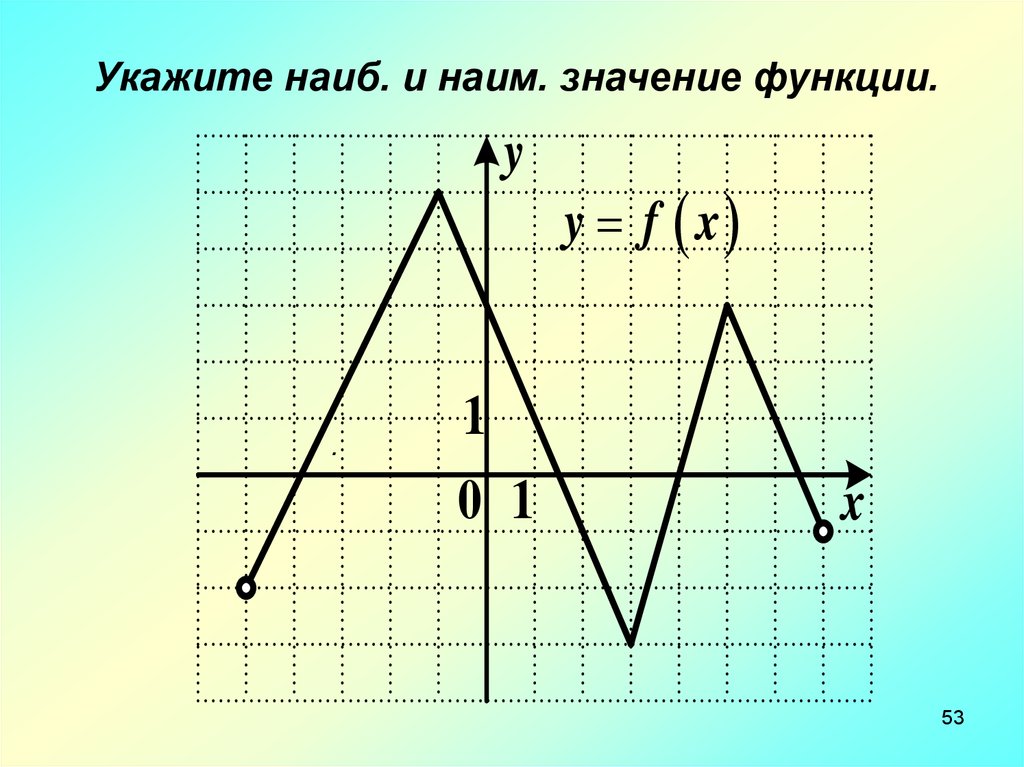
53.
Укажите наиб. и наим. значение функции.y
.
y f x
1
0 1
x
53









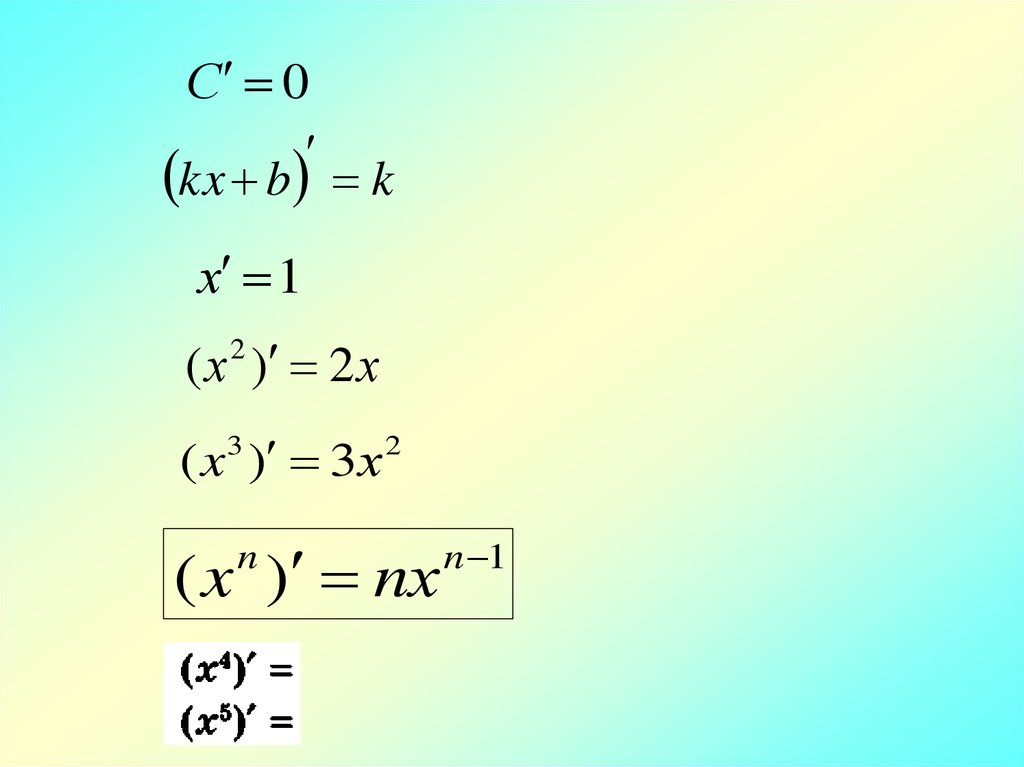
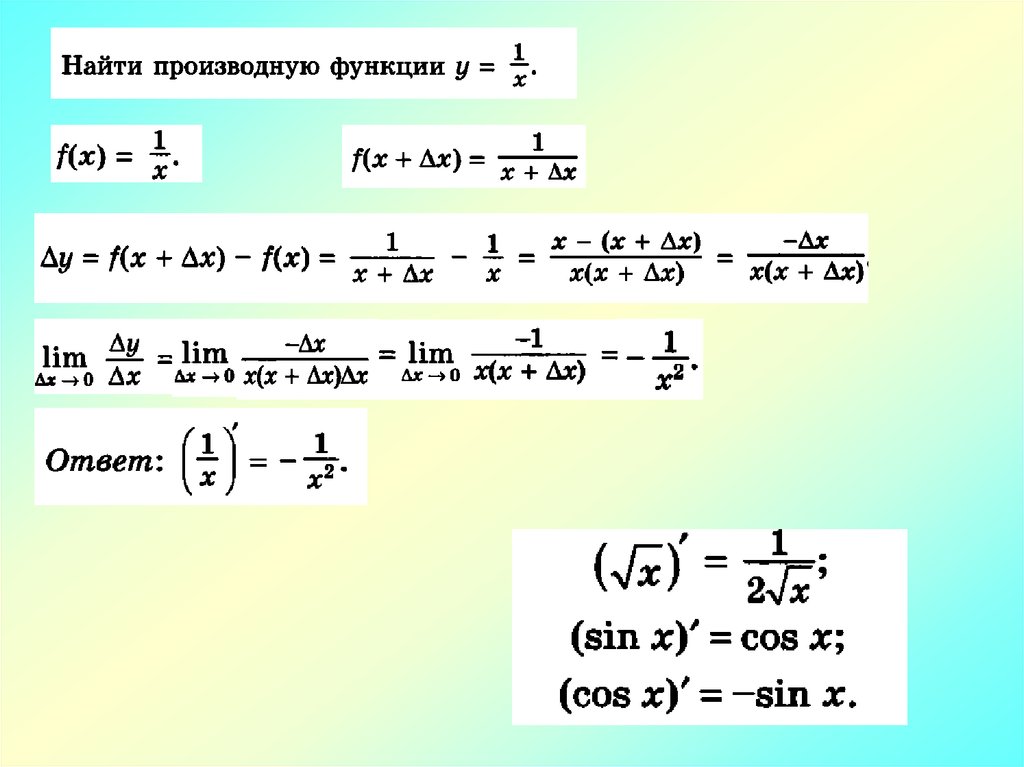










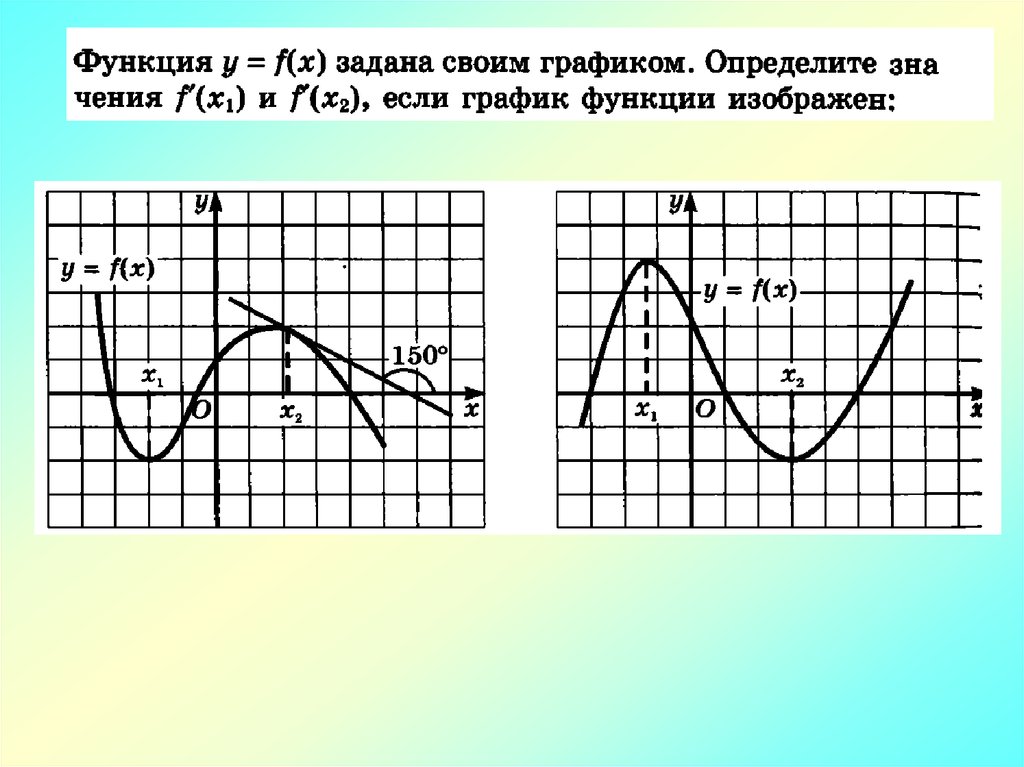
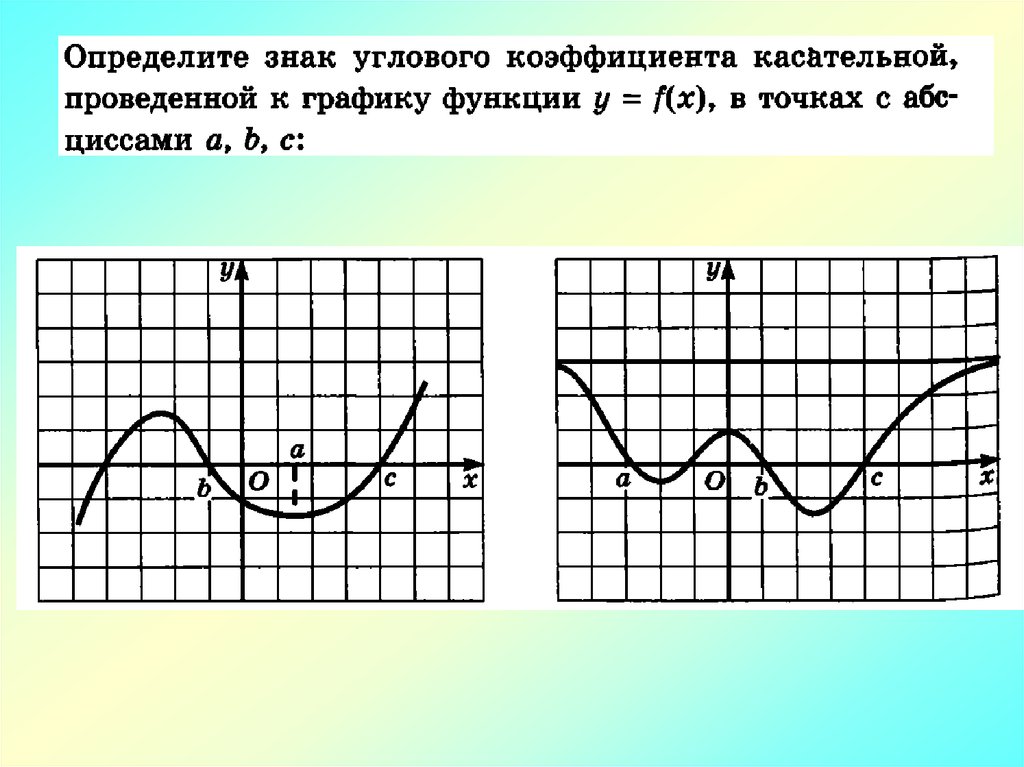
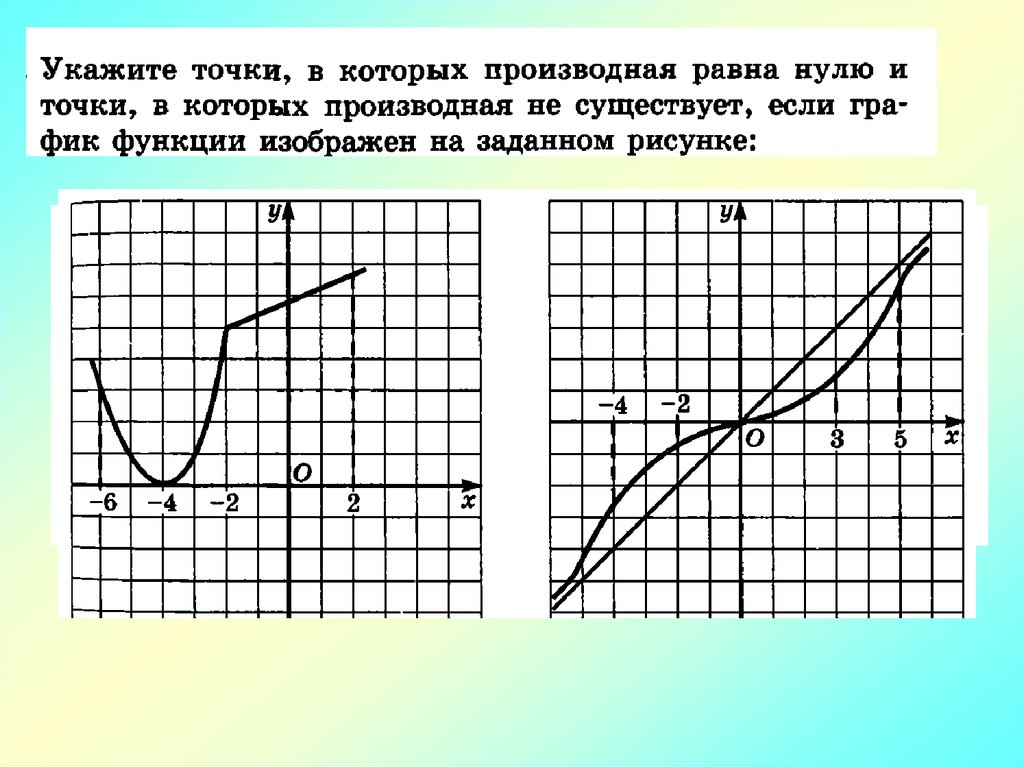

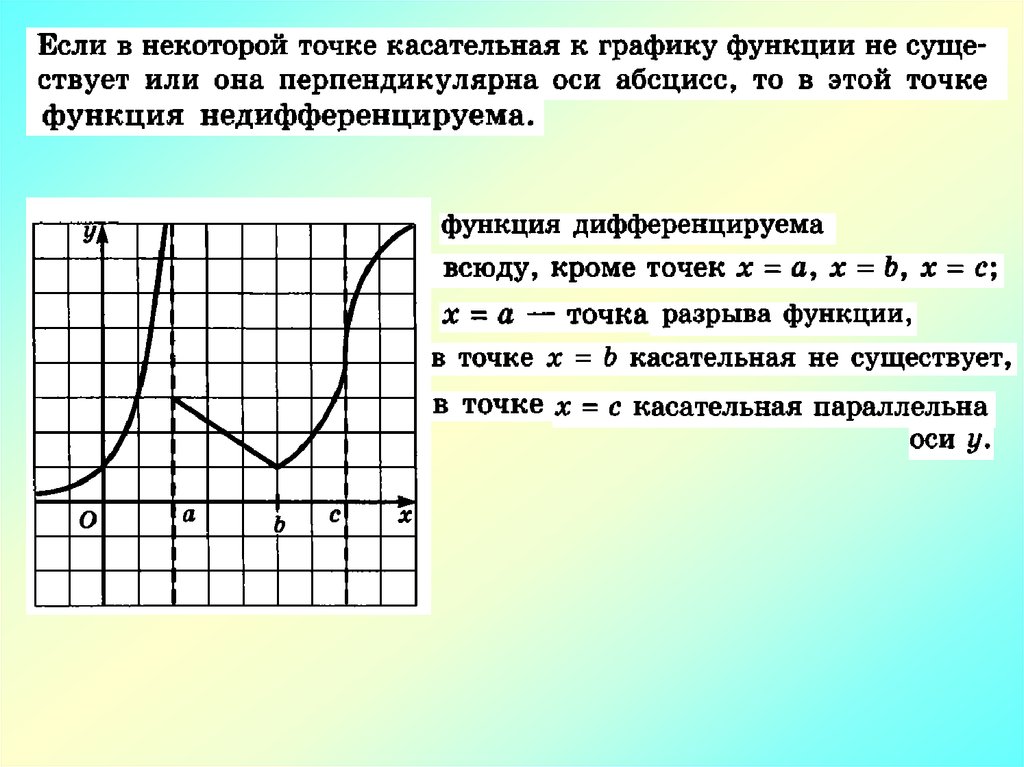



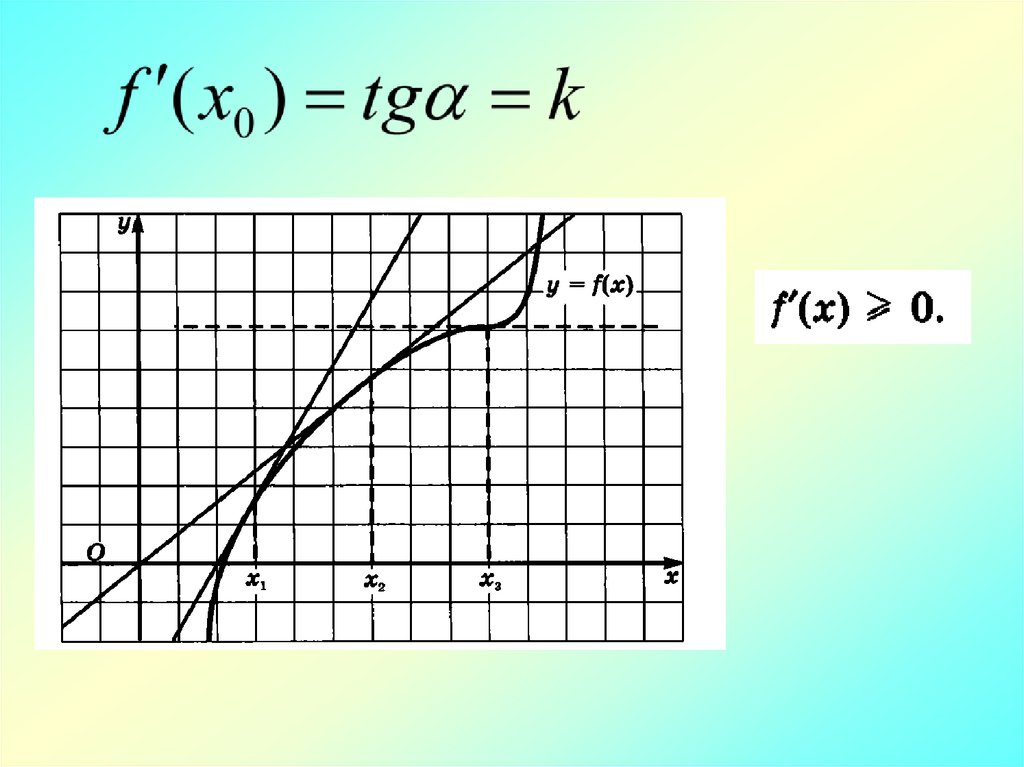
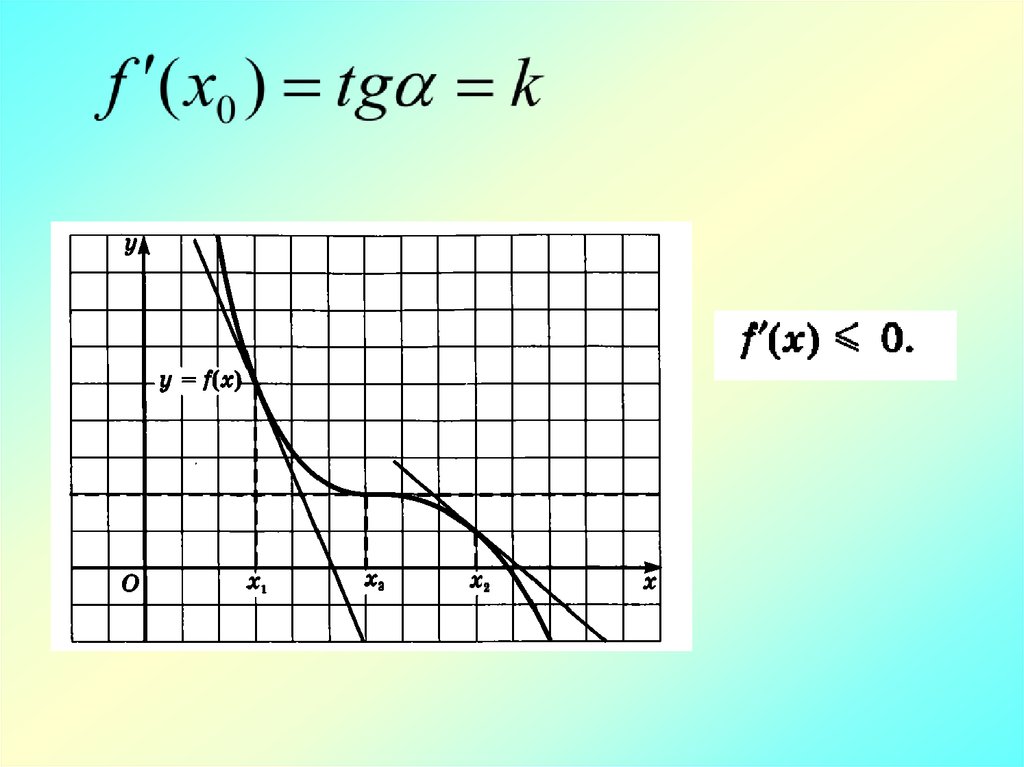











 Математика
Математика








