Похожие презентации:
Решение задачи Бхаскары
1.
В Древней Индии были распрост раненыпубличные соревнования в решении
трудных задач. Задачи част о
облекались в ст ихот ворную форму.
Вот задача Бхаскары:
Обезьянок резвых ст ая, всласт ь
поевши, развлекалась.
Их в квадрат е част ь восьмая на
полянке забавлялась.
А двенадцат ь по лианам ст али
прыгат ь, повисая.
Сколько ж было обезьянок, т ы скажи
мне, в эт ой ст ае?
2. Решение задачи Бхаскары
Пусть было х обезьянок, тогда на полянеx
забавлялось 8 обезьянок,
а 12 – прыгали по лианам.
Получим уравнение
2
x
12 x
8
х ² – 64х + 12∙64 = 0,
х1 = 16 или х2 = 48.
Задача имеет два решения.
3.
Теория без практики мертва или бесплодна,практика без теории невозможна или пагубна.
Для теории нужны знания, для практики,
сверх всего того, и умение.
А.Н. Крылов
4.
Ист орические сведения:Квадрат ные уравнения впервые вст речают ся в
работ е индийского мат емат ика и аст ронома
Ариабхатты.
Другой индийский ученый Брахмагупт а (VII в)
изложил общее правило решения квадрат ных
уравнений, кот орое практ ически совпадает с
современным.
5. Цель
Отработка общихумений и навыков при
решении квадратных
уравнений.
6. Задачи
-Повторить определениеквадратного уравнения и его виды,
- формулы решения полного
квадратного уравнения
-Решение квадратных уравнений по
теореме Виета,
-Развивать внимание навыки
самоконтроля и самооценки,
-Развивать мышление, творческие
способности.
7. Разбейте следующие уравнения на группы по какому-либо признаку: Изобразите информацию в виде графического приема «гроздья»
1) 3х²+8х-7=07) 3х2 – 5х – 4 =0
2) х2 + 3х+ 1 = 0
8) х2 - 24x = 0
3) 7-5х+х²=0
9) 16х2 – 4 = 0
4) 5х2 = 0
10) – 0,1х2 + 10 = 0
5) 169 –х2 = 0
11) - x2 – 3x + 15 = 0
6) 7х + 13 -6х²=0
12) x2 – 5x = 0
8. Квадратные уравнения
Квадратные уравненияах²+bх+с = 0
9. Разбейте следующие уравнения на группы по какому-либо признаку: Изобразите информацию в виде графического приема «гроздья»
1) 3х²+8х-7=07) 3х2 – 5х – 4 =0
2) х2 + 3х+ 1 = 0
8) х2 - 24x = 0
3) 7-5х+х²=0
9) 16х2 – 4 = 0
4) 5х2 = 0
10) – 0,1х2 + 10 = 0
5) 169 –х2 = 0
11) - x2 – 3x + 15 = 0
6) 7х + 13 -6х²=0
12) x2 – 5x = 0
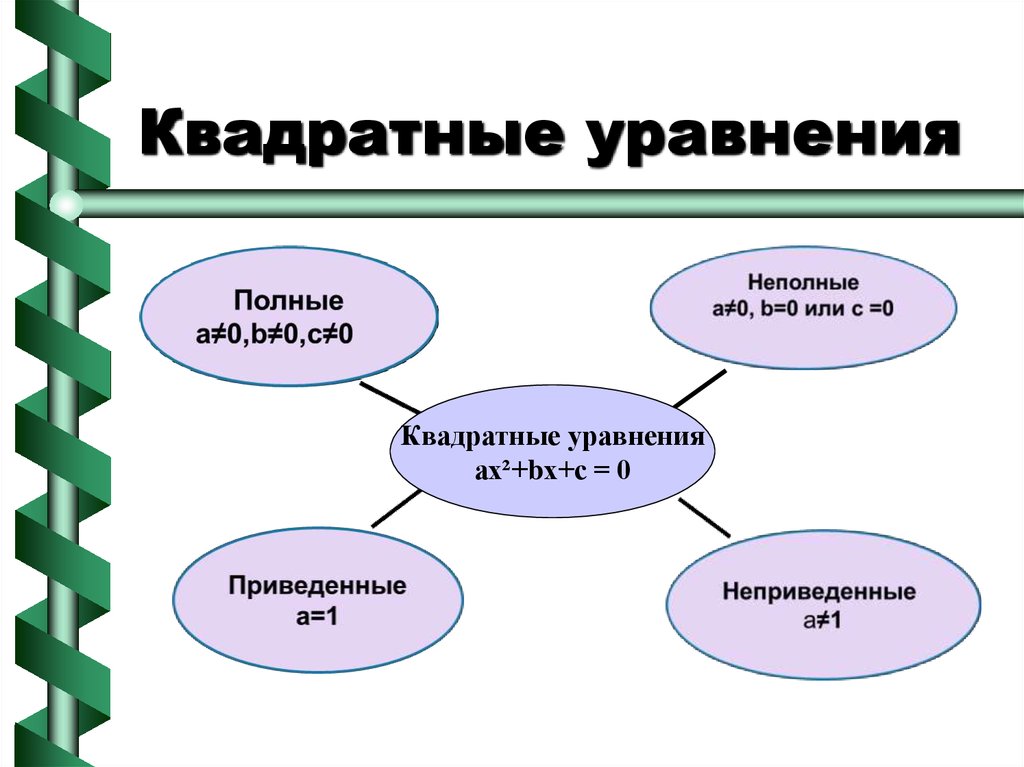
10. Квадратные уравнения
Квадратные уравненияах²+bх+с = 0
11. Разбейте следующие уравнения на группы по какому-либо признаку: Изобразите информацию в виде графического приема «гроздья»
1) 3х²+8х-7=07) 3х2 – 5х – 4 =0
2) х2 + 3х+ 1 = 0
8) х2 - 24x = 0
3) 7-5х+х²=0
9) 16х2 – 4 = 0
4) 5х2 = 0
10) – 0,1х2 + 10 = 0
5) 169 –х2 = 0
11) - x2 – 3x + 15 = 0
6) 7х + 13 -6х²=0
12) x2 – 5x = 0
12.
Приведенныех2 + 3х+ 1 = 0
7-5х+х²=0
Полные
1) 3х²+8х-7=0
2) х2 + 3х+ 1 = 0
3) 7-5х+х²=0
7х + 13 -6х²=0
3х2 – 5х – 4 =0
- x2 – 3x + 15 = 0
Неприведенные
3х²+8х-7=0
- x2 – 3x + 15 = 0
Неполные
5х2 = 0
169 –х2 = 0
х2 - 24x = 0
16х2 – 4 = 0
– 0,1х2 + 10 = 0
x2 – 5x = 0
13.
14.
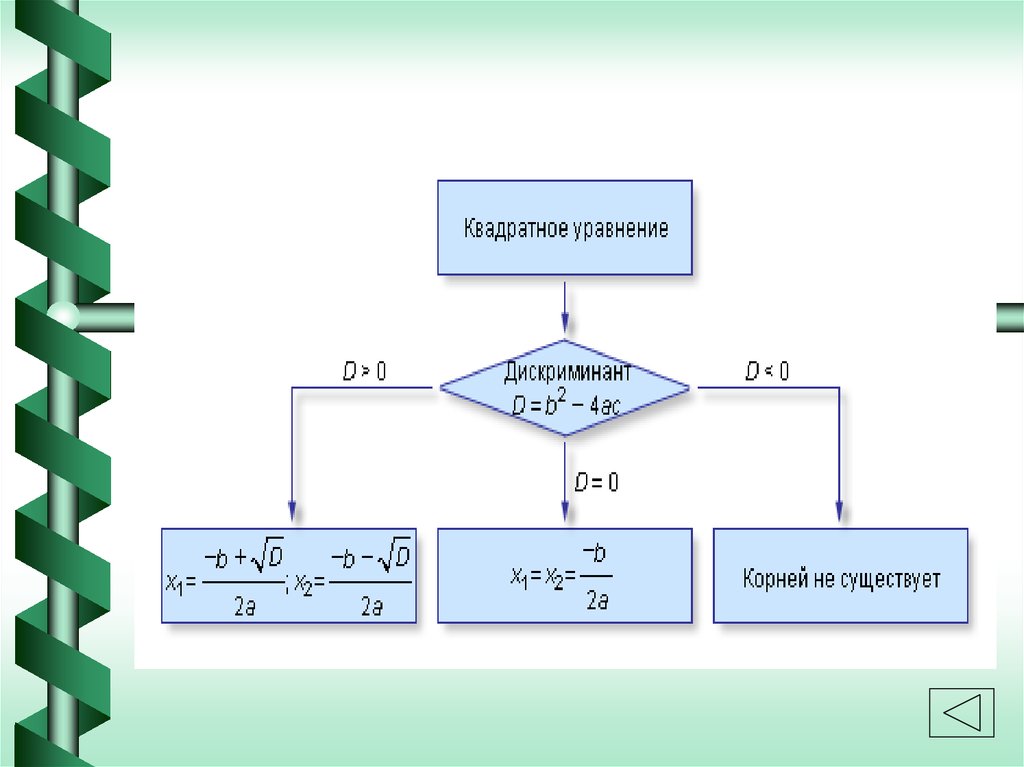
ах2+вх+с=01. Найди значения а, b и с;
2. Вычисли дискриминант: D = b2 – 4ac;
D < 0 корней нет;
D = 0 один корень (два одинаковых);
D > 0 два различных корня.
15.
16.
Теорема ВиетаСумма корней приведённого квадратного уравнения
x2 + px + q = 0 равна его второму коэффициенту p
с противоположным знаком,
а произведение – свободному члену q.
x1 + x2 = –p;
x1 x2 = q.
В случае неприведённого квадратного
уравнения ax2 + bx + c = 0 :
c
b
x1+x2 =
x1x2 =
a
a
17. Тренажёр
• Внимательно читайтезадание.
• Время ограничено. На
выполнение тренажёра 10
минут.
18. Самостоятельная работа
• 1. В работе 4 задания. Определикритерии оценки
Каждое верно решенное задание оценивается в 1 балл,
неверное – 0 баллов.
4 баллов – «5»
3 балла – «4»
2 балла - «3»
0-1 баллов – «2».
• 2. Выбери вариант (их четыре)
• 3. Реши уравнения.
• 4. Оцени свою работу.
19. А1. Определите количество корней квадратного уравнения:
Вариант х2-8х-84=01
1) 0 2) 1 3) 2 4) 3
Вариант 36х2-12х+1=0
2
1) 0 2) 1 3) 2 4) 3
Вариант х2-22х-23=0
3
1) 0 2) 1 3) 2 4) 3
Вариант х2-2х+5=0
4
1) 0 2) 1 3) 2 4) 3
20. А2. Решите уравнение:
Вариант1
х2+5х=0
1)0;5 2) 1;5 3) 0;-5 4) 1;-5
Вариант
2
х2-49=0
1)0;49 2)±49 3)±74)нет корней
Вариант
3
-х2+7х=0
1) 7;0 2) -7;0 3) 1;7 4)-1;7
Вариант
4
4х2+17=0
1) 17/4
3)
2) -17/4
17
4
4) нет корней
21. А3. Найдите больший корень уравнения:
Вариант 1 2х2-7х+5=01) 1 2) 2,5 3) 3 4) 3,5
Вариант 2 3х2-2х-1=0
1) 1 2) -1/3 3) -1 4) 3
Вариант 3 4х2-7х+3=0
1) 1 2) -3/4 3) 3/4 4) 3
Вариант 4 2х2-9х+7=0
1) 0 2) 1 3) 7/2 4) 2
22. А4. Решите уравнение:
Вариант 1Вариант 2
4х²-1 - 3х²+8
3
5
2х-3х²
-
7х²-х
5
4
=1
= х² 1) ±5; ±√2
2
3) нет корней
Вариант 3 х²- 3 х+ 1 =0
4
Вариант 4
Х-3
4
1) 1\2;1\4
3) нет корней
8
+ 2х+3 = х²-11
6
1) ±1;±4
3) ±1; ±17
12
1) ±2
3) 8; -1
2) ±2
4) нет корней
2) 0; 13\57
4) ±√2
2) ±√5
4) ±5
2) -9; 4
4) нет корней
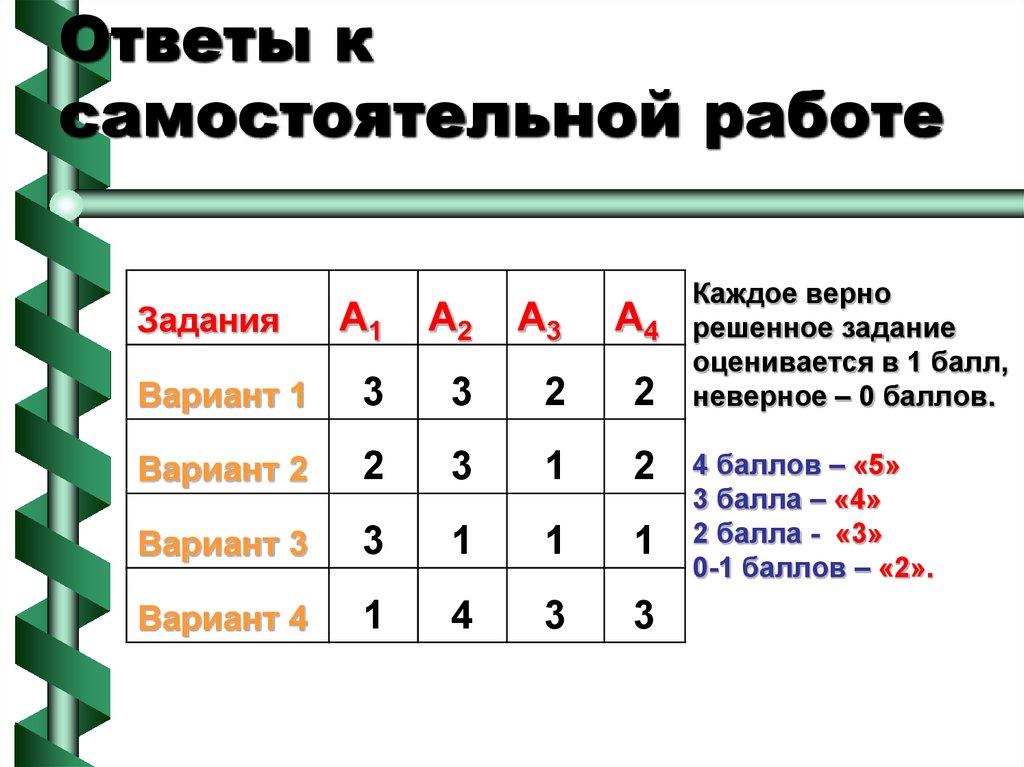
23. Ответы к самостоятельной работе
А1А2
А3
А4
Вариант 1
3
3
2
2
Вариант 2
2
3
1
2
Вариант 3
3
1
1
1
Вариант 4
1
4
3
3
Задания
Каждое верно
решенное задание
оценивается в 1 балл,
неверное – 0 баллов.
4 баллов – «5»
3 балла – «4»
2 балла - «3»
0-1 баллов – «2».
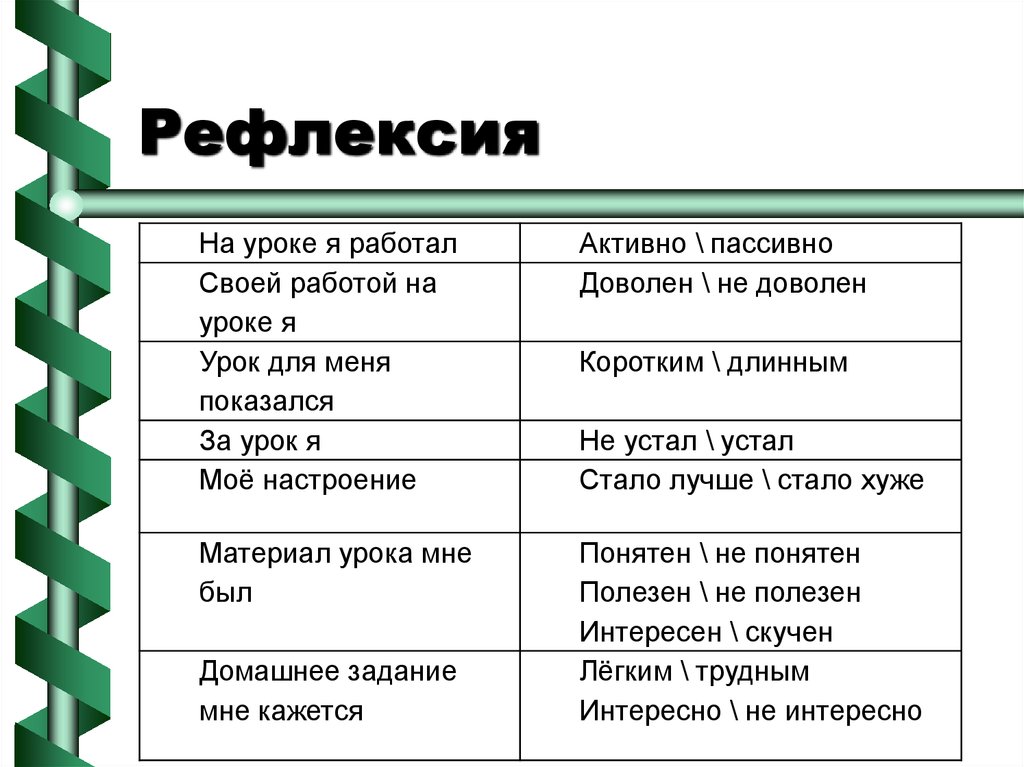
24. Рефлексия
На уроке я работалСвоей работой на
уроке я
Урок для меня
показался
За урок я
Моё настроение
Активно \ пассивно
Доволен \ не доволен
Материал урока мне
был
Понятен \ не понятен
Полезен \ не полезен
Интересен \ скучен
Лёгким \ трудным
Интересно \ не интересно
Домашнее задание
мне кажется
Коротким \ длинным
Не устал \ устал
Стало лучше \ стало хуже
25. Домашнее задание (выбор)
• Тест 8• №596 (д,е); 650 (а,б);
656 (а-в)
26.
Урок сегодня завершён.Дружней вас не сыскать.
Но каждый должен знать:
Познание, упорство, труд
К прогрессу приведут!





















 Математика
Математика








