Задачи с параметрами

1. Задачи с параметрами

2. Определение

Уравнение f(x;a)=0, где хпеременная, а – произвольное
действительное число,
называют уравнением с
параметром а.

3. Аналитический способ решения задач с параметрами

Этот способ повторяет стандартные
процедуры нахождения ответа в
задачах без параметра.
Аналитический способ решения задач с
параметрами – самый трудный, он
требует высокой грамотности и
наибольших усилий по овладению им.

4. 1) Решить уравнение: ax=1

На первый взгляд представляется
возможным сразу дать ответ: х = 1/а
Однако при a=0 данное уравнение
решений не имеет.
Ответ:
Если a=0, то нет решений;
Если a≠0, то
х = 1/а

5. 2) Решить уравнение

x ≠ ±2,
ax+2a = x+1,
a
x+ 1
= 2
x− 2 x − 4
(a-1)x=1-2a, a≠1.
1 − 2a
x=
a− 1
Найдем значения a, которые приводят к недопустимым
значениям x.
1− 2a
x= 2, 2=
a− 1
2a − 2= 1− 2a
3
4a= 3, a=
4
3
Следовательно, а не может равняться 4 .

6.

1− 2a
x = − 2, − 2 =
,
a− 1
− 2a + 2= 1− 2a , 0a = −1,
0а = - 1 невозможно ни при каких значениях а
Ответ:
3
1− 2a
Если a≠ 1 и a ≠ 4 , то x= a− 1
Если
3
a ≠ 1 и при a= , решений нет.
4

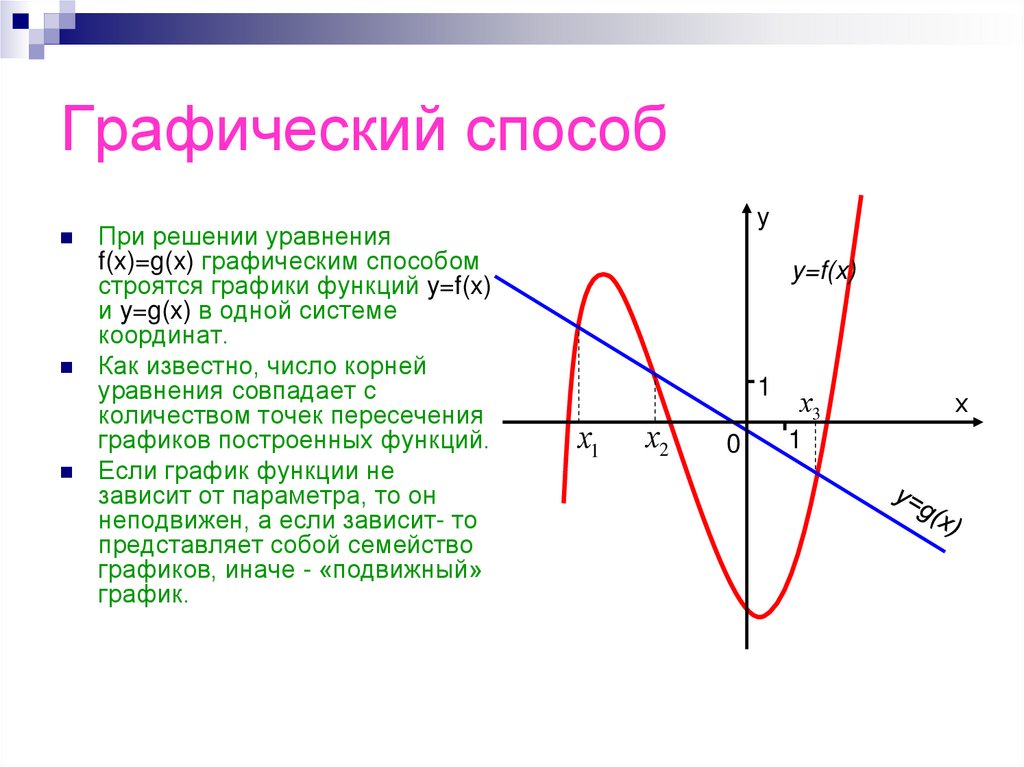
7. Графический способ

При решении уравнения
f(x)=g(x) графическим способом
строятся графики функций y=f(x)
и y=g(x) в одной системе
координат.
Как известно, число корней
уравнения совпадает с
количеством точек пересечения
графиков построенных функций.
Если график функции не
зависит от параметра, то он
неподвижен, а если зависит- то
представляет собой семейство
графиков, иначе - «подвижный»
график.
у
y=f(x)
1
х1
х2
0
х3
1
х

8.

у
Функция
у=b
Графики
таких функций –
семейство
параллельных
оси Ох прямых.
b=4
b=2
1
0
1
х
b=0
b = -2
b = -4

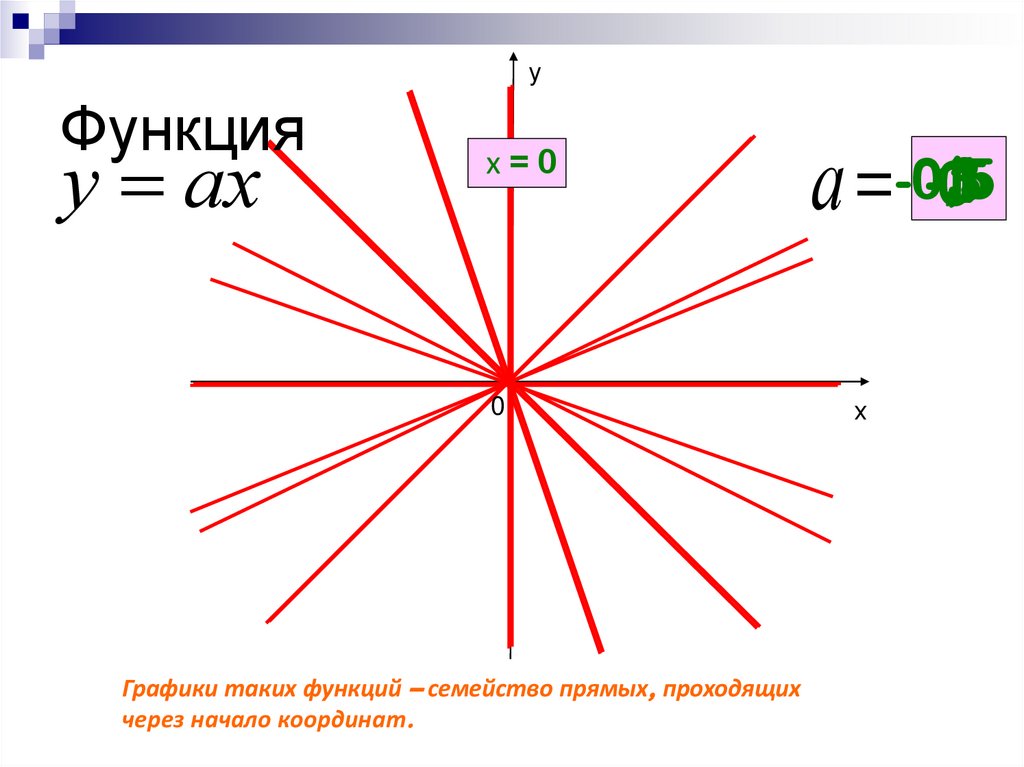
9. Функция

у
Функция
у ах
х=0
0
Графики таких функций – семейство прямых, проходящих
через начало координат.
0,5
1
-3
-1
0
а -0,5
х

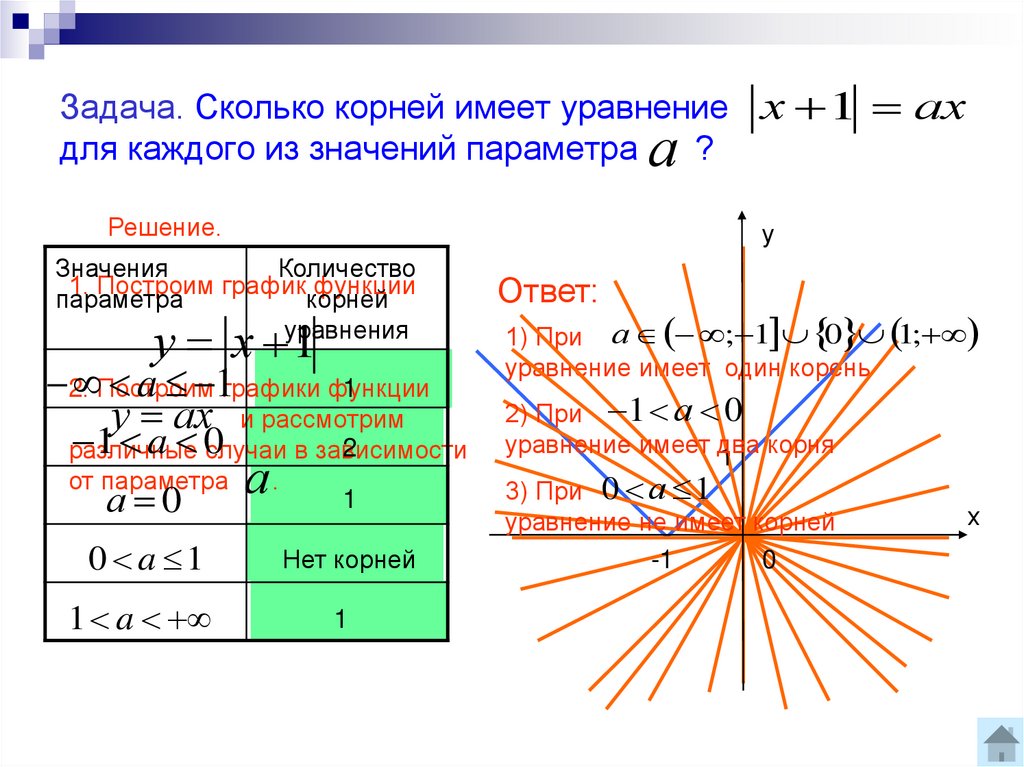
10. Задача. Сколько корней имеет уравнение для каждого из значений параметра ?

Задача. Сколько корней имеет уравнение х 1 ах
для каждого из значений параметра
?
а
Решение.
у
Значения
Количество
1. Построим график функции
параметра
корней
уравнения
у х 1
2. Построим
a 1графики функции
1
у ах и рассмотрим
1 a 0случаи в зависимости
2
различные
от параметра
.
1
а 0
а
0 a 1
1 a
Нет корней
1
Ответ:
1) При а ; 1 0 1;
уравнение имеет один корень
2) При 1 а 0
уравнение имеет два
1 корня
3) При 0 а 1
уравнение не имеет корней
-1
0
х

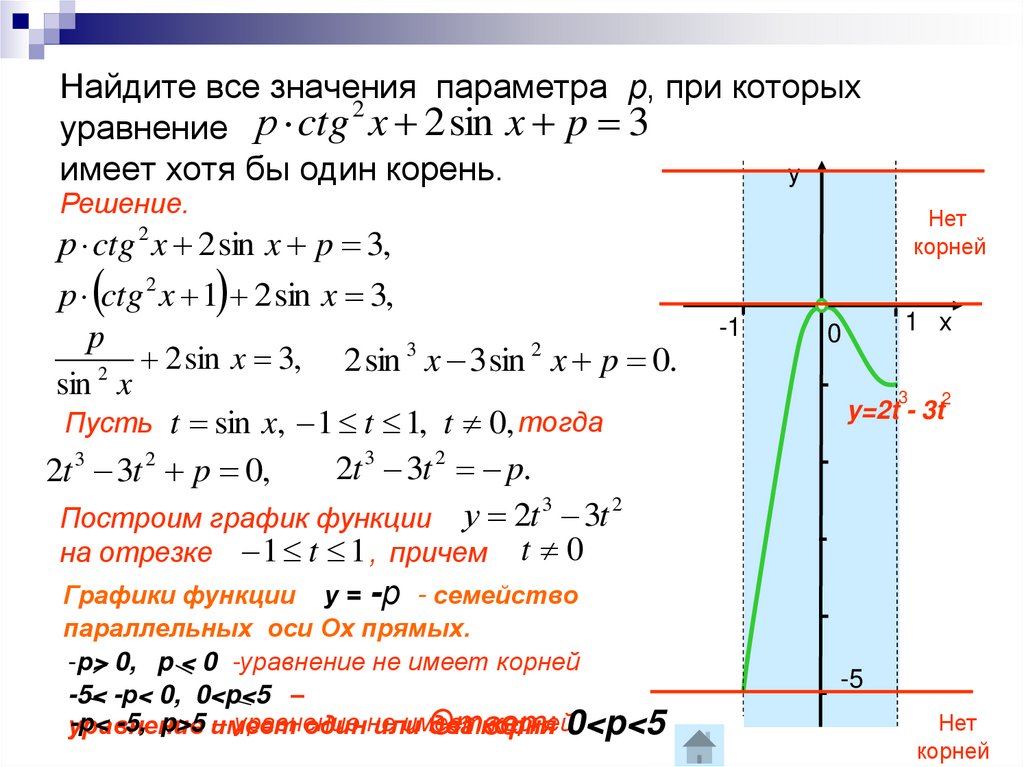
11. Найдите все значения параметра р, при которых уравнение имеет хотя бы один корень.

Найдите все значения параметра р, при которых
2
уравнение р ctg x 2 sin x p 3
имеет хотя бы один корень.
у
Решение.
Нет
корней
р ctg x 2 sin x p 3,
2
р ctg 2 x 1 2 sin x 3,
р
3
2
2
sin
x
3
,
2
sin
x
3
sin
x p 0.
2
sin x
Пусть t sin x, 1 t 1, t 0, тогда
2t 3 3t 2 p.
2t 3 3t 2 p 0,
3
2
Построим график функции у 2t 3t
на отрезке 1 t 1 , причем t 0
Графики функции у = -р - семейство
параллельных оси Ох прямых.
-р> 0, p < 0 -уравнение не имеет корней
-5< -р< 0, 0<p<5 –
-р< -5, p>5 имеет
– уравнение
имеет
корней0<p<5
уравнение
одинне
или
два корня
Ответ:
-1
1 х
0
3
2
y=2t - 3t
-5
Нет
корней

12. Решение уравнений относительно параметра

При решении задач этим способом
переменные х и а принимаются
равноправными и выбирается та переменная,
относительно которой аналитическое
решение признается более простым. После
естественных упрощений возвращаемся к
исходному смыслу переменных х и а и
заканчиваем решение.

13. Задача. Решить уравнение

х - 2а х + а - 1 = 0
2
4
2
Решение.
Данное уравнение четвертой степени
относительно переменной х и является
квадратным относительно параметра а .
2ах + а - 1 = 0
х - 2а
а - 2х а + х - 1 = 0
22
4
2
2
2
4
2
а
х
1,
2 х4 2 4
аD
1 4. 2
1, 2 4 x 4 x ,
2
а х 1;
2
х 2 а 1,
2
х а 1.

14.

Возможны различные случаи. Результаты
исследования этих случаев запишем в таблицу:
а
; 1 1
х2 а 1
2
х а 1
х
Ответ:
Нет
действительных
0
х 0
1;1
1
1;
+
0
+
+
+
х1 а 1,
х1 0
х1, 2 а 1,
х2 а 1
х2 2 , х3, 4 а 1
х3 2
если а<-1, то действительных корней нет;
если а= -1, то
х 0 ;
если -1<a<1, то х1
а 1, х2 а 1 ;
если а=1, то х1 0, х2 2 , х3 2 ;
если а>1, то х1, 2 а 1, х3, 4 а 1.

15. Задача 1. Найдите все значения а, при которых область определения функции содержит ровно три целых числа.

а, при которых область определения функции
Задача 1. Найдите все значения
у а х х ( х 3) logx a а8 3loga x
содержит ровно три целых числа
.
x
3
9 6 x logx a
a
0, 5
22
Решение.
Преобразуем выражение в скобках:
х 3 logx a
8 3 loga x
9 6 x logx a
а х
a
x
a 22
а х а х 3 а 8 х 3 х 3 а 2 х а11 а 2 х а 3 а 8 х 3 х 3 а 2 х а11
х
3
а 2 х а 3 х 3 а8 х 3 а 3 а 3 х 3 а 2 х а8 .
Областью определения данной функции
является множество решений системы неравенств:
а 3 х 3 а 2 х а 8 0,
х 0,
x 1.

16.

Решим первое неравенство: а 3 х 3 а 2 х а8 0.
f ( x) a a .
Пусть
g ( x) a 3 x 3 ,
Функция
g (x )- убывающая при любом значении параметра а.
2x
8
g ( x) 0 при х а .
Функция f (x ) - монотонно убывает или возрастает в зависимости от
f ( x) 0 при х 4 .
значения параметра а.
Рассмотрим различные случаи в зависимости от значений параметра
а.
1. 0<a<1, х (0; а ) ( 4; )
Это множество включает в себя
бесконечное число целых чисел.
х (а;4)
2. 1<a<4
g (x )
Это множество может
содержать только два целых числа.
3. а>4,
х (4; а)
+
f (x)
Данное множество содержит
три целых числа, если 7 а 8
Ответ: а 7;8
а
+
0
a
+
1
_
_
4
_
_
х
х

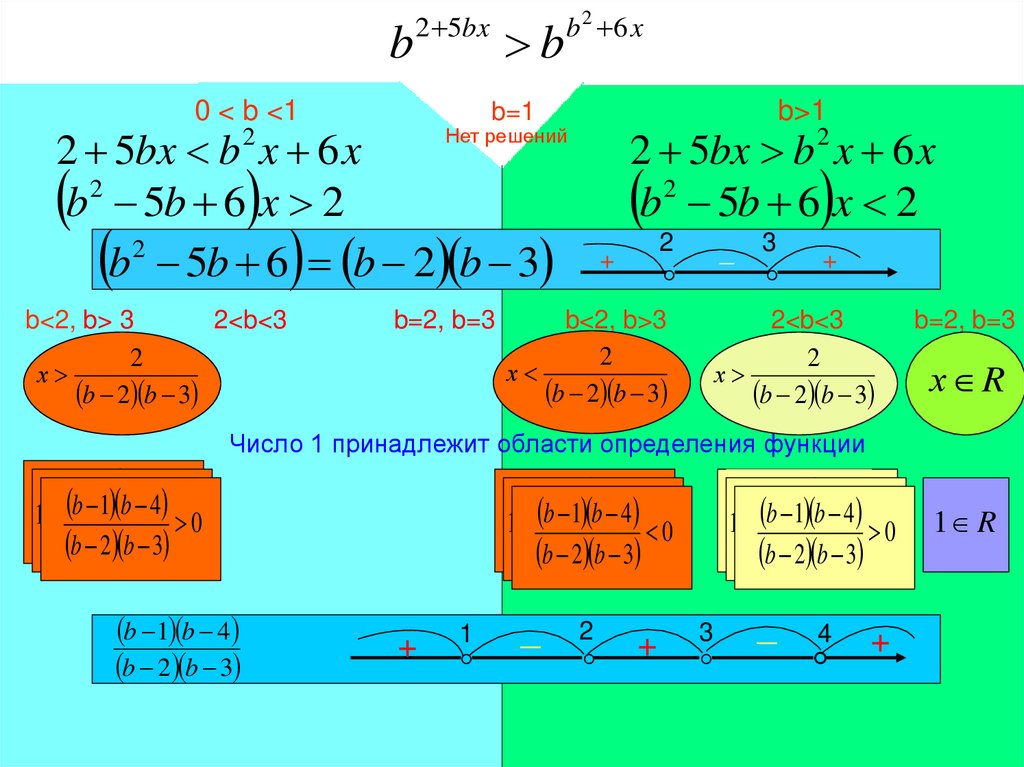
17. Задача 2. Найдите все положительные значения параметра b, при которых число 1 принадлежит области определения функции

у b2 5bx bb x 6 x
2
52
Решение.
Найдем область определения данной функции.
b
2 5bx
b
b
2 5bx
b 2 x 6 x
b
0
b2 6 x
Для положительных значений b рассмотрим три различных случая

18.

b
2 5bx
0 < b <1
b
b2 6 x
b>1
b=1
2 5bx b x 6 x
2
b 5b 6 x 2
b 2 5b 6 b 2 b 3
b<2, b> 3
2<b<3
2
х
b 2 b 3
2 5bx b x 6 x
2
b 5b 6 x 2
Нет решений
2
b=2, b=3
2
2
+
_
b<2, b>3
2
х
b 2 b 3
3
+
2<b<3
2
х
b 2 b 3
b=2, b=3
х R
Число 1 принадлежит области определения функции
2
1 b 1 2b 4
1 b 2 b 3 00
bb 22 bb 33
b 1 b 4
b 2 b 3
2
1 b 1 2b 4
1 b 2 b 3 00
b b 22 bb 33
+
1
_
2
+
2
1 b 1 2b 4
1 b 2 b 3 00
bb 22 bb 33
3
_
4
+
1 R

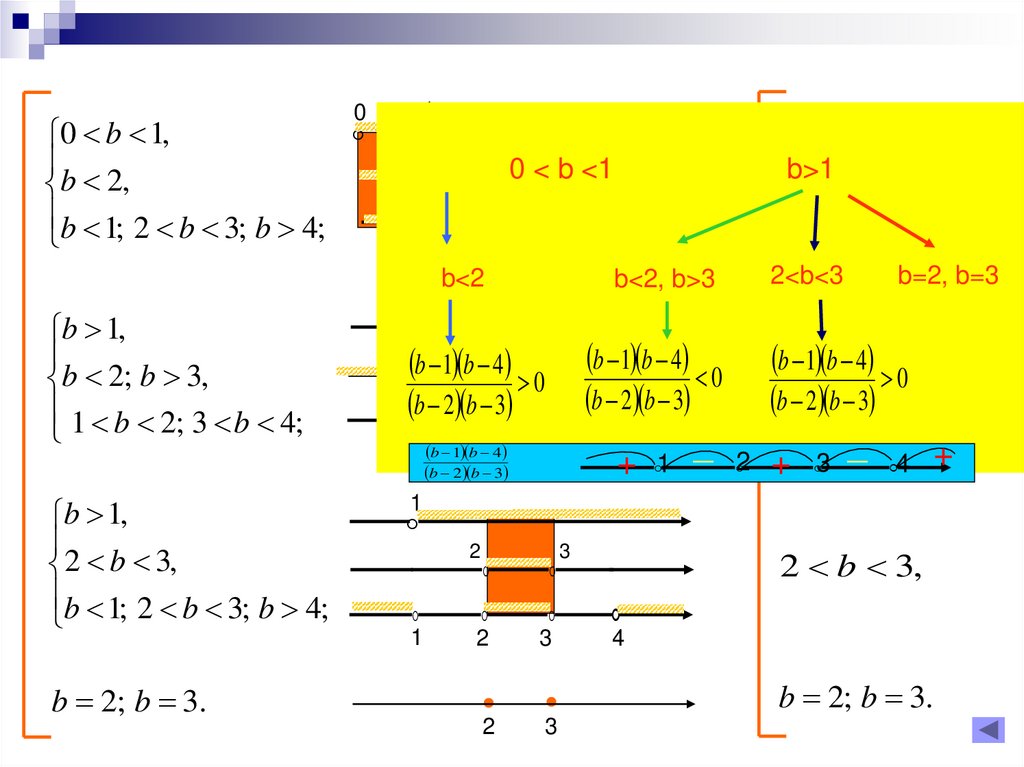
19.

0
0 b 1,
b 2,
b 1; 2 b 3; b 4;
1
1
2
b 2; b 3.
2<b<3
b<2, b>3
b=2, b=3
1
b 1 b2 4 0 3 b 1 b 4 0
b 2 b 3 b 2 b 3
1 b 1 b2 4
4
3
+
b 2 b 3
b 1,
2 b 3,
b 1; 2 b 3; b 4;
4
3
b<2
b 1,
b 2; b 3,
1 b 2; 3 b 4;
0b>1
b 1,
0 < b <1
1
_
1 b 1b b 42 ; 30 b 4,
b 2 b 3
2
+
3
_
4
+
1
2
1
2
3
3
2 b 3,
4
b 2; b 3.
2
3

20.

Ответ: при
b 0;1 1;4
число 1 принадлежит
области
определения функции.

21.

Решение
а х
х
х 3 logx a
a
8 3 loga x
x
3
9 6 x logx a
у
a
22
х
х 3
8
3
3
2х
11
= а а а х х а а
2х
3
8
3
3
2х
11
= а а а х х а а
2х
3
3
8
3
3
= а а х а х а
=
а
3
х3 а 2 х а8
а х х х 3 logx a a 8 3 loga x
x
3
9 6 x logx a
a 22
х
х 3
8
3
3
2х
11
= а а а х х а а
1
2х
3
8
3
3
2х
11
= а а а х х а а
2х
3
3
8
3
3
= а а х а х а
=
а
3
х3 а 2 х а8
0
Ответ: а=5
.
а
х
1
х