Похожие презентации:
Решение квадратных уравнений
1.
Тема : «Решение квадратных уравнений»Учитель: Казьмин А.Н.
2.
Квадратным уравнением называютуравнение вида
2
ax
+ bx + c = 0,
где коэффициенты a, b, с – любые
действительные числа, причем a ≠ 0
3.
Если a = 0, тоbx + с = 0 – линейное уравнение
4.
b=0ax2 + с = 0;
с=0
квадратные
ax2 + bx = 0;
неполные
уравнения
b = 0, с = 0
ax2 = 0
5.
а) 6a 2 3a5
б) 5x 2 x
2
7
7
в) x 2 x
6
3
b
b
x
г) x 2
a
2a
6.
1) x 2 – 6x x 2 – 6x 32 (x – 3)27 2
7
7 2
7
2
x ( ) (x )
2) x
x x
3
6
3
6
2
b 2
b
b
b 2
2
)
3) x x x
x ( ) (x
a
2a
a
2a
2
7.
x 7x 02
x (x 7) 0
x 0 èëè x 7 0,
x 0 èëè x 7.
8.
9x 4 02
9x 4
2
4
x
9
2
x
3
2
9.
x2 – 6x 5 0,(x2 – 2 • 3x + 32) – 9 +
5 = 0,
(x – 3)2 – 4 = 0 ,
(x – 3)2 – 22 = 0 ,
(x – 3 – 2)(x – 3 + 2) =
0,
(x – 5)(x – 1) = 0,
x – 5 = 0 или x – 1 = 0,
x=5
или x = 1.
10.
3x2 + 7x + 1 = 011.
63x2 - 109x + 133 = 0?
12.
3x 2 7x 1 0,3x 7x 1 0, |: 3
ax bx c 0
2
ax bx c 0 |: a
7
1
x x
0,
3
3
7
49 49
1
x2 2 x
–
0,
6
36 36
3
b
c
x x 0
a
a
b
b 2 b 2 c
2
x 2 x ( ) ( ) 0
2a 2a
2a
a
7
49 1
(x )2
6
36 3
b 2 b2 c
(x ) 2
2a
4a
a
7
37
(x )2
6
36
b 2 b2 4ac
(x )
2a
4a 2
2
2
x
7
6
x
37
36
7
37
6
6
x 1,2
x
7
37
6
36
x
7 37
6
7
37
6
6
2
2
13.
b 2 b2 4ac(x )
2a
4a 2
(x
b 2
D
) 2
2a
4a
D b 2 4ac
если D < 0, то корней нет
если D = 0, то один корень
b
0,
2a
b
x
2a
x
если D > 0, то два корня
x
b
D
2a
4a2
x
b
D
2a 2a
b
D
2a
4a2
x
b
D
2a
2a
b
D
2a 2a
x
b D
2a
x
x
x
x
x 1,2
b D
2a
b
D
2a 2a
b D
2a
14. Алгоритм решения квадратных уравнений:
ax2 + bx + c = 0b=,
с=
1) a = ,
2) D = b2 – 4ac;
3) если D < 0, то корней нет
если D = 0, то один корень
x
b
2a
если D > 0, то два корня.
x 1,2
b D
2a
15.
3x 2 7x 1 0;a 3, b 7, c 1;
D b2 4ac
D 49 4 3 1 49 12 37, D 0, два корня
b D
x 1,2
2a
x 1,2
x1
7 37
6
7 37
6
7 37
x2
6
16. № 810 (б)
3х2 – 3х + 4 = 0а = 3, b = –3, с = 4
D = b2 – 4ас,
D (–3)2 – 4 3 4 9 – 48 – 39 , D 0
корней нет
17. Самостоятельная работа
№807(a)№807(в)
№807(б)
Решить уравнение: 3x2 + 2x – 5 = 0
Самостоятельная работа
18. Эталон для самопроверки
№807(а)№807(б)
№807(в)
x 2 3x 24 0
x 2 16x 64 0
x 2 2x 5 0
a 1, b 3, c 24
a 1, b 16, c 64
a 1, b 2, c 5
D b 2 4ac
D b 2 4ac
D b 2 4ac
D 32 4 1 ( 24)
D ( 16)2 4 1 64
D ( 2)2 4 1 5
105
0
-16
D 0, 2 корня
D 0, 1 корень
D 0, корней нет
19.
3x 2 2x 5 0a 3, b 2, c 5
D b 2 4ac
D 2 2 4 3 ( 5) 4 60 64, D 0, 2 корня
b D
x 1,2
2a
2 64
x 1,2
2 3
2 8
x 1,2
6
5
x 1 ;
x2 1
3
20. Составьте задачу по чертежу
x дм70 дм2
(x 3) дм
21.
x(x 3) 70x 2 3x 70
x 2 3x 70 0
a 1, b 3, c 70
D b2 4ac
D 32 4 1 ( 70) 9 280 289,D 0, 2 корня
b D
x 1,2
2a
3 289
2 1
3 17
x 1,2
2
x 1,2
x1 10;
x2 7
22. Домашнее задание
§20, №№ 806(б, г), 810(в, г), 819(б),830*
Домашнее задание
23.
№830x – гипотенуза
x – 32 – один катет
x – 9 – другой катет
Теорема Пифагора: с2 = a2 + b2
x2 = (x – 32)2 + (x – 9)2
24.
x 2 (x 32)2 (x 9)2x 2 64x 1024 x 2 18x 81 x 2 0
x 2 82x 1105 0
a 1, b 82, c 1105
D b 2 4ac
D ( 82)2 4 1 1105 6724 4420 2304,D 0, 2 корня
b D
x 1,2
2a
82 2304 82 48
x 1,2
2 1
2
34
x 1
17;
2
130
x2
65
2







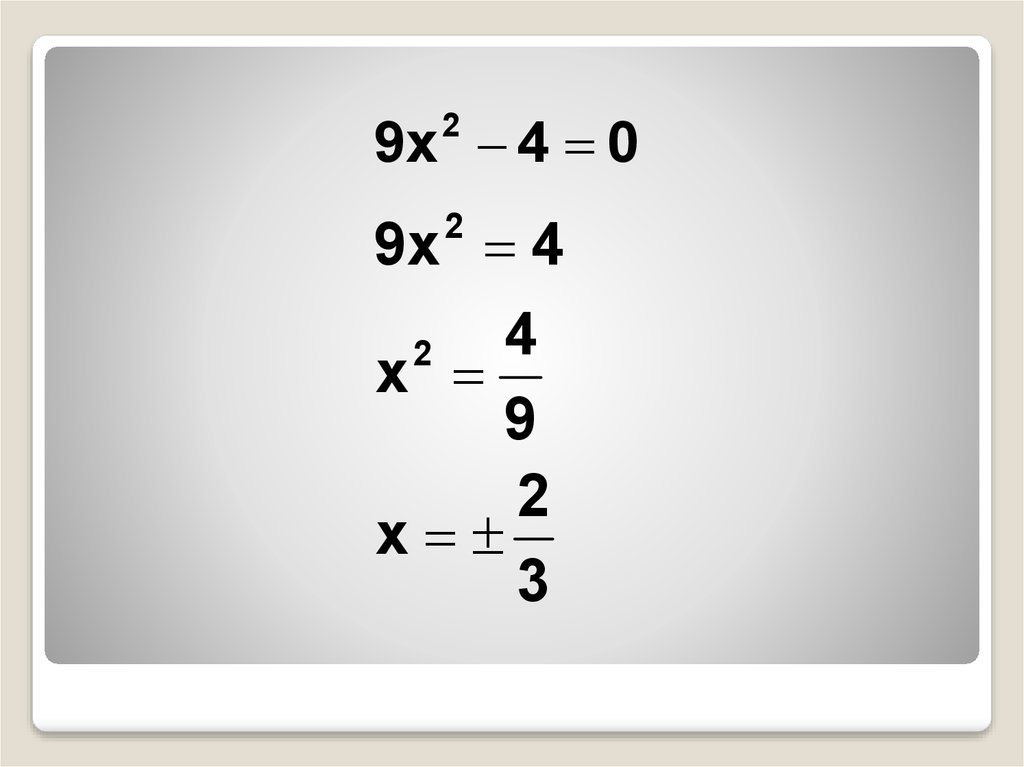
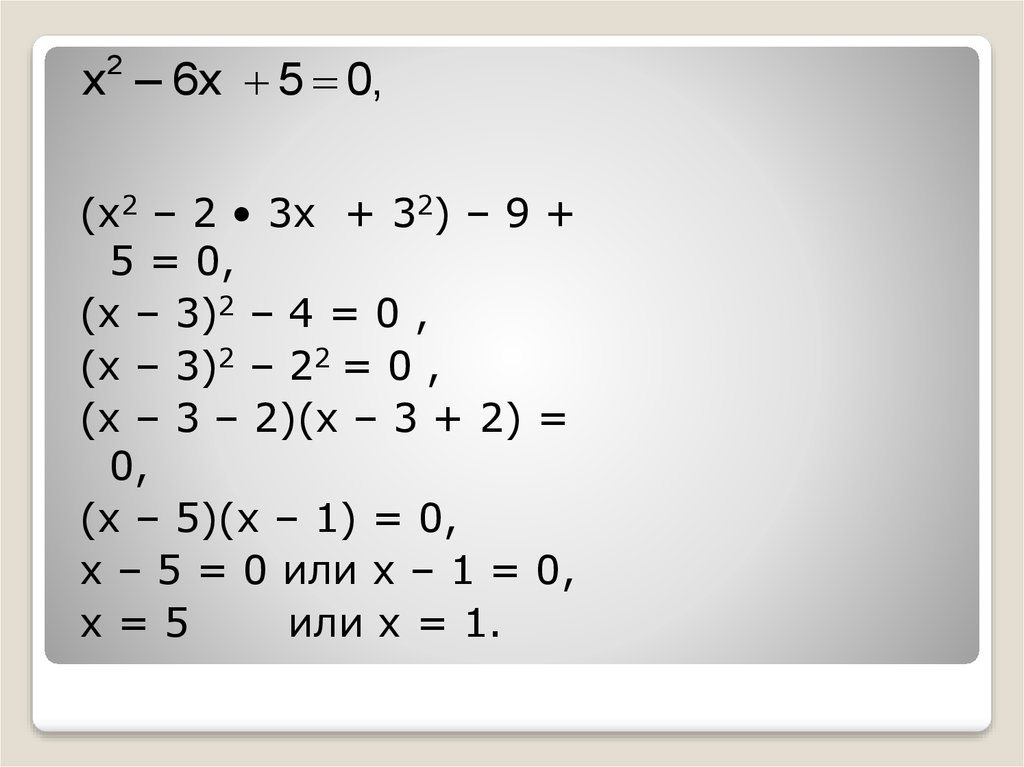
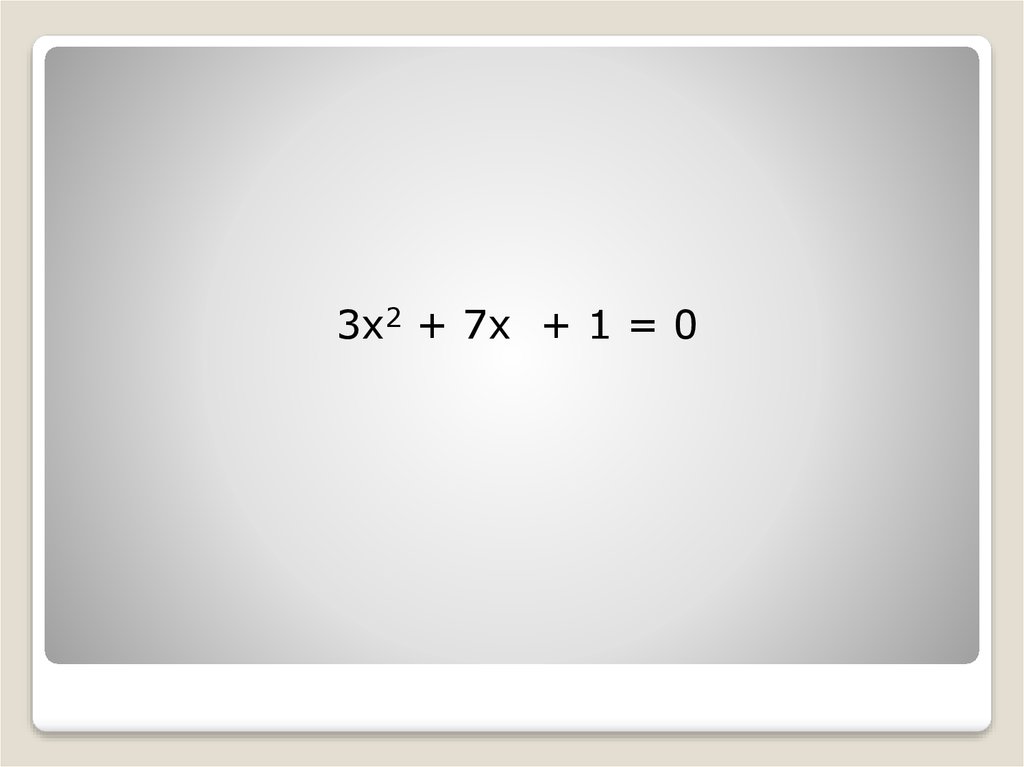














 Математика
Математика








