Похожие презентации:
Основы логики
1.
Муниципальное общеобразовательное учреждениеЛицей №10 имени Д.И. Менделеева
Выполнила:
учитель информатики и ИКТ
Чеснокова Татьяна Сергеевна
Клин, 2009
2. Цель презентации:
познакомиться с основами логики.Задачи презентации:
• дать определение терминам “логика”,
основных форм мышления,
логических операций;
• составить таблицы истинности
логических операций;
• познакомиться с логическими законами.
3. Содержание
1. Историческая справка.Слайд 4
2. Логика. Алгебра логики.
Слайд 5
3. Формы мышления (понятие, высказывание,
умозаключение). Слайды 6 – 8. Слайд 6
4. Алгебра высказываний.
3.1. Логическое умножение.
3.2. Логическое сложение.
3.3. Логическое отрицание.
3.4. Логическое следование.
3.5. Логическое равенство.
Слайд 9
Слайд 10
Слайд 11
Слайд 12
Слайд 13
5. Логические законы. Слайды 14 – 17.
Слайд 14
4. Историческая справка
Английский математикДжордж Буль
разработал основы
алгебры, в которой
используются только 0 и 1
(алгебра логики, булева
алгебра).
(1815 -1864)
К содержанию
5.
Логика – это наука о способах и формахмышления.
Алгебра логики – это математический
аппарат, с помощью которого
записывают (кодируют), упрощают,
вычисляют и преобразовывают
логические высказывания.
К содержанию
6. Формы мышления
1. Понятие.2. Высказывание.
3. Умозаключение.
Понятие – форма мышления,
фиксирующая основные,
существенные признаки объекта.
К содержанию
7.
Высказывание – повествовательноепредложение, о котором можно
сказать, истинно оно или ложно.
Умозаключение – это форма мышления,
с помощью которой из одного или
нескольких суждений может быть
получено новое суждение.
Задание. Приведите примеры простых
и сложных высказываний.
8.
Высказывание или нет?Сейчас светит солнце.
Сократ – человек.
История – интересный предмет.
Луна является спутником Земли.
Превосходно!
Как пройти к музею Чайковского?
У меня есть кошка.
9. Алгебра высказываний
Логическоеумножение
(конъюнкция,
операция “и”).
sign: Λ
Истинно тогда и
только
тогда,
когда истинны все
входящие в него
простые
высказывания.
A
B
АΛB
0
0
0
0
1
0
1
0
0
1
1
1
К содержанию
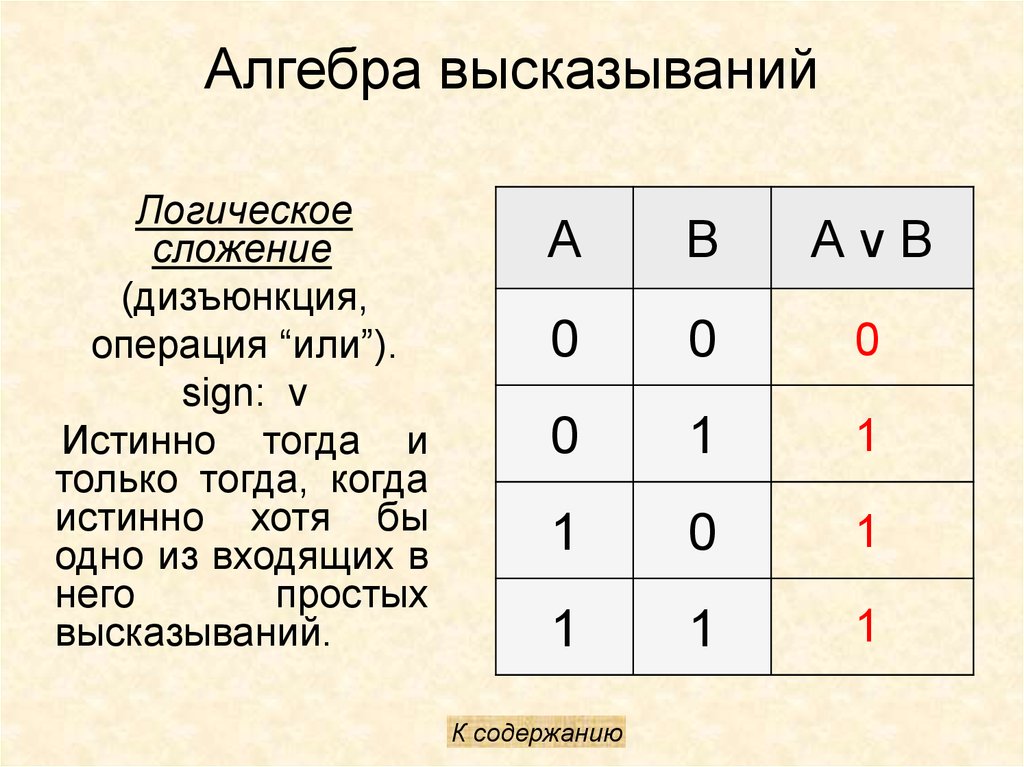
10. Алгебра высказываний
Логическоесложение
(дизъюнкция,
операция “или”).
sign: v
Истинно тогда и
только тогда, когда
истинно хотя бы
одно из входящих в
него
простых
высказываний.
A
B
АvB
0
0
0
0
1
1
1
0
1
1
1
1
К содержанию
11. Алгебра высказываний
Логическое отрицание(инверсия,
операция “не”).
sign: А
Инверсия делает
истинное высказывание
ложным и ,наоборот,
ложное – истинным.
К содержанию
А
А
0
1
1
0
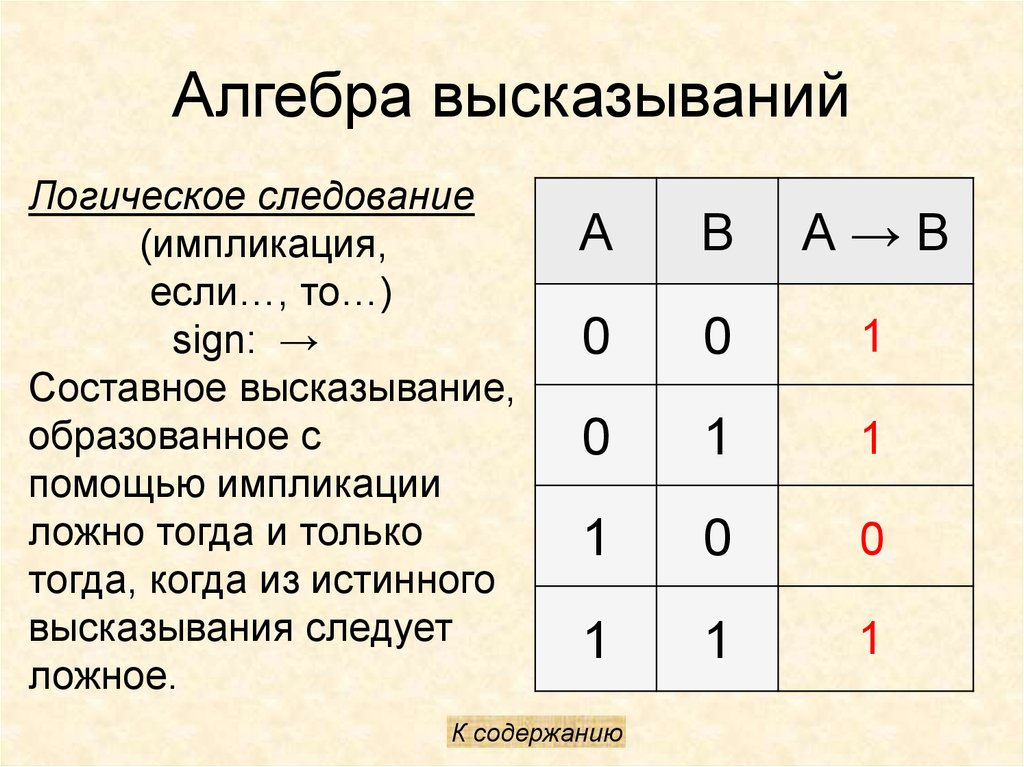
12. Алгебра высказываний
Логическое следование(импликация,
если…, то…)
sign: →
Составное высказывание,
образованное с
помощью импликации
ложно тогда и только
тогда, когда из истинного
высказывания следует
ложное.
A
B
А→B
0
0
1
0
1
1
1
0
0
1
1
1
К содержанию
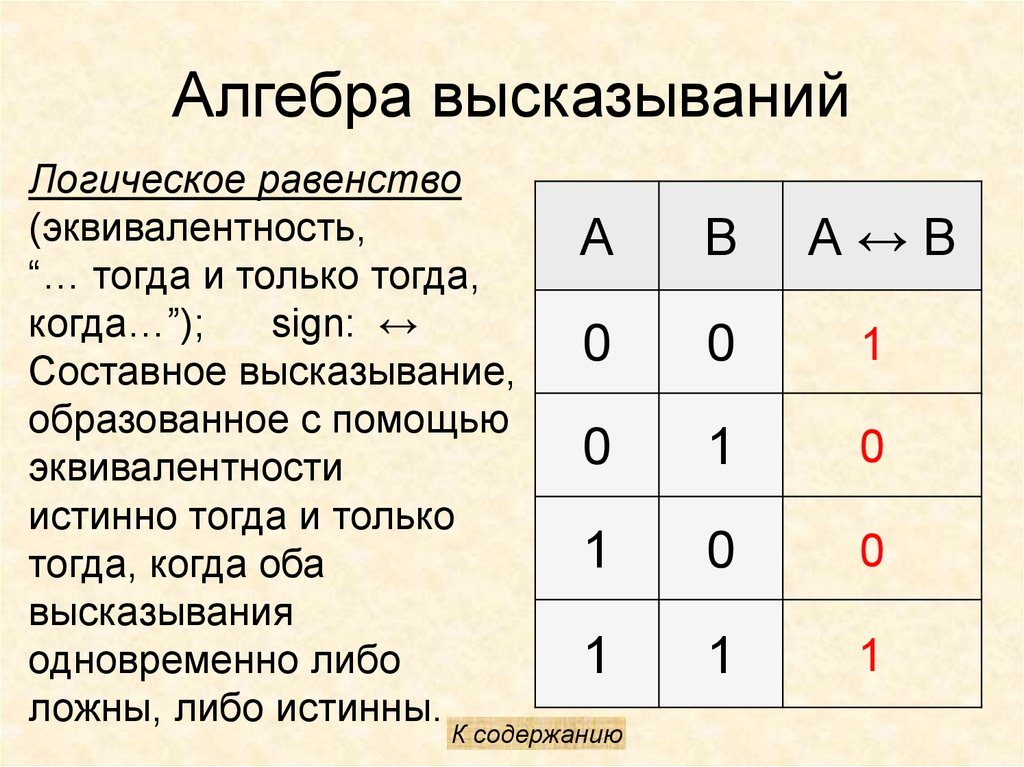
13. Алгебра высказываний
Логическое равенство(эквивалентность,
“… тогда и только тогда,
когда…”);
sign: ↔
Составное высказывание,
образованное с помощью
эквивалентности
истинно тогда и только
тогда, когда оба
высказывания
одновременно либо
ложны, либо истинны.
A
B
А↔B
0
0
1
0
1
0
1
0
0
1
1
1
К содержанию
14. Логические законы
1. Закон тождества: А А2. Закон противоречия:
А А 0
3. Закон исключения третьего:
4. Закон двойного отрицания:
А А 1
А А
5. Законы де Моргана:
А В А В
А В А В
К содержанию
15. Логические законы
6. Закон коммутативности:А В В А
А В В А
7. Закон ассоциативности:
А В С А В С
А В С А В С
8. Закон дистрибутивности:
А В С А В А С
А В С А В А С
16. Логические законы
9. Закон идемпотентности:А А А
А А А
10. Законы исключения констант:
А 1 1
А 1 А
А 0 0
А 0 А
11. Закон поглощения:
А А В А
А А В А
17. Логические законы
12. Закон исключения (склеивания):А В А В В
А В А В В
13. Закон контрапозиции:
А В В А














 Информатика
Информатика








