Похожие презентации:
Модели статистического прогнозирования
1.
Моделистатистического
прогнозирования
2.
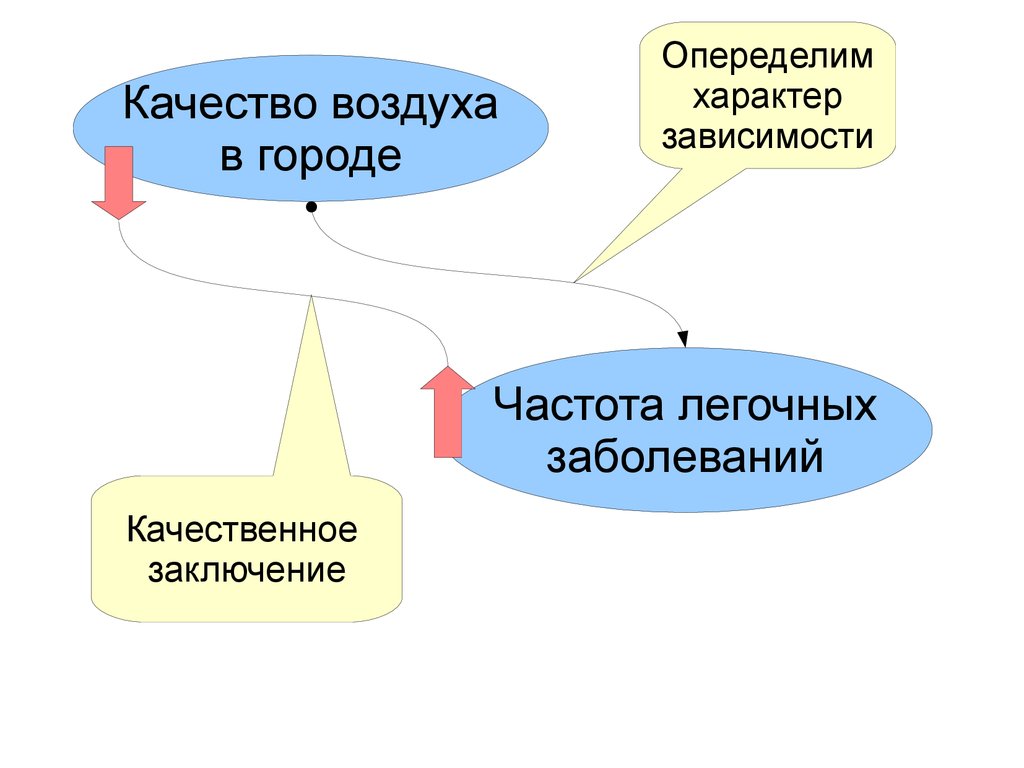
Качество воздухав городе
Опеределим
характер
зависимости
Частота легочных
заболеваний
Качественное
заключение
3.
Уточнение характера зависимостиПримеси в воздухе,
влияющие на
здоровье
Число заболеваний
Сильно влияющие
Оксид
углерода
Несильно влияющие
Обобщение
Анализ
Сбор
экспериментальных
данных
Должно
быть
много
4.
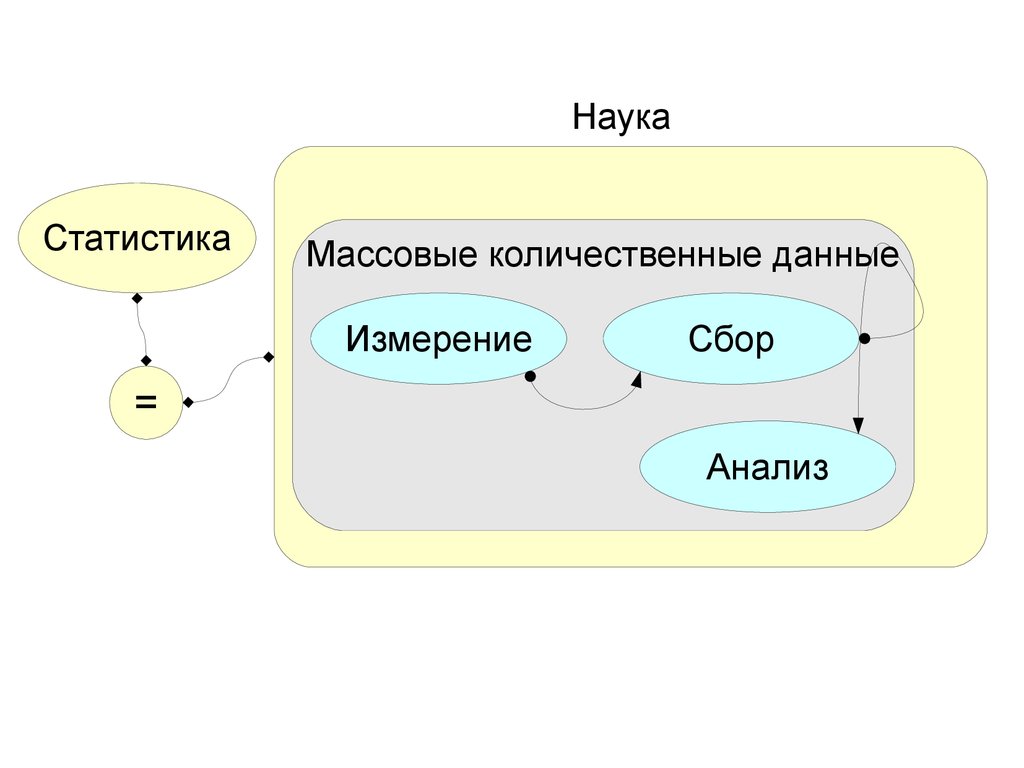
НаукаСтатистика
Массовые количественные данные
Измерение
Сбор
=
Анализ
5.
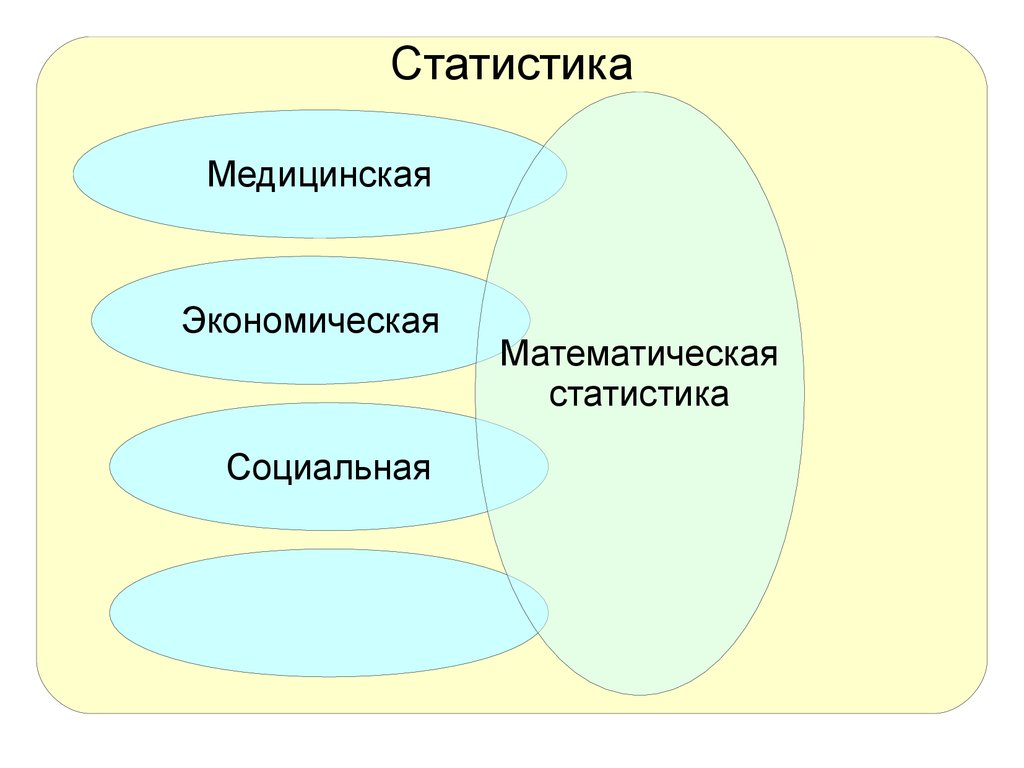
СтатистикаМедицинская
Экономическая
Социальная
Математическая
статистика
6.
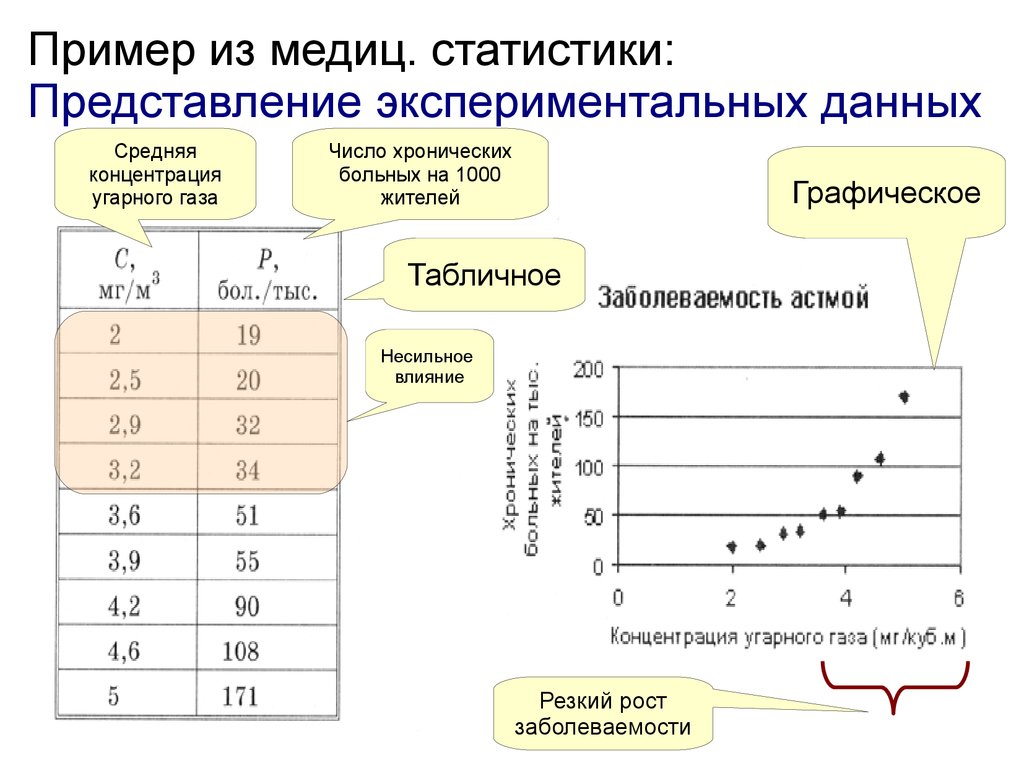
Пример из медиц. статистики:Представление экспериментальных данных
Средняя
концентрация
угарного газа
Число хронических
больных на 1000
жителей
Графическое
Табличное
Несильное
влияние
Резкий рост
заболеваемости
7.
Носят оценочныйхарактер
Приближённые,
усреднённые
Статистические данные
Верно
отражают
подбор
Оценочная
модель
Характер зависимости
величины
Матем. методы
Математическая модель
P=f(C)
Формульное
выражение
функциональной
зависимости
График должен
проходить близко
к экспер. точкам
8.
Приближенныеданные
Искомая функция
График проходит
через все
экспериментальные
точки
Основные требования
Достаточная простота
Отклонения точек от
графика
Минимальны
Равномерны
Нет смысла
Слишком сложный
вид функции
Регрессионная
модель
Удобно использовать
в дальнейших вычислениях
9.
Получение регрессионноймодели
Методы
Подбор вида функции
Наиболее используемые функции
y=ax+b
вычисления
параметров
Не имеет
строгого
решения
Метод
наименьших
квадратов
y=aln(x)+b
y=ax2+bx+c
y=axb
y=ax3+bx2+cx+d
y=aebx
18 век,
К. Гаусс
Вычисление
параметров функции
Опыт
Интуиция
a
Слепой
перебор
b
c
d
10.
у = ах + b ― линейная функция;2
у = ах + bх + с ― квадратичная
функция;
у = а ln(х) + b ― логарифмическая
функция;
bx
у = ае
― экспоненциальная
функция;
b
у = ах ― степенная функция.
11.
Квадратичная функция называется вматематике полиномом второй степени.
Иногда используются полиномы и
более высоких степеней, например
полином третьей степени имеет вид:
3
2
у = ах + bх + сх + d.
12.
Во всех этих формулах:х ― аргумент,
у ― значение функции,
а, b, с, d ― параметры функции,
ln(х) ― натуральный логарифм,
е ― константа, основание
натурального логарифма.
13.
Искомая функция должна бытьпостроена так, чтобы
сумма квадратов отклонений y-координат
всех экспериментальных точек
от y-координат графика функции
была минимальной
МНК
Искомая функция
(y1э-y1ф)2
(yiэ-yiф)2
k
Σ
(y
-y
)
iЭ
iф
i=1
1
2
min
(y2э-y2ф)2
14.
Статистическая обработка данныхИспользуемые
математические
пакеты
программ
МНК
Критерии соответствия
Построение любой
функции
Регрессионная
модель
График
Тренд
15.
С первого взгляда хочется отбраковатьвариант линейного тренда.
График линейной функции ― это прямая.
Полученная по МНК прямая
отражает факт роста заболеваемости от
концентрации угарного газа,
но по этому графику трудно что-либо
сказать о характере этого роста.
А вот квадратичный и экспоненциальный
тренды правдоподобны.
16.
Полученные функции:линейная функция: у = 46,361х - 99,881;
экспоненциальная функция:
у = 3,4302 е 0,7555х ;
квадратичная функция:
у = 21,845х2 - 106,97х + 150,21.
17.
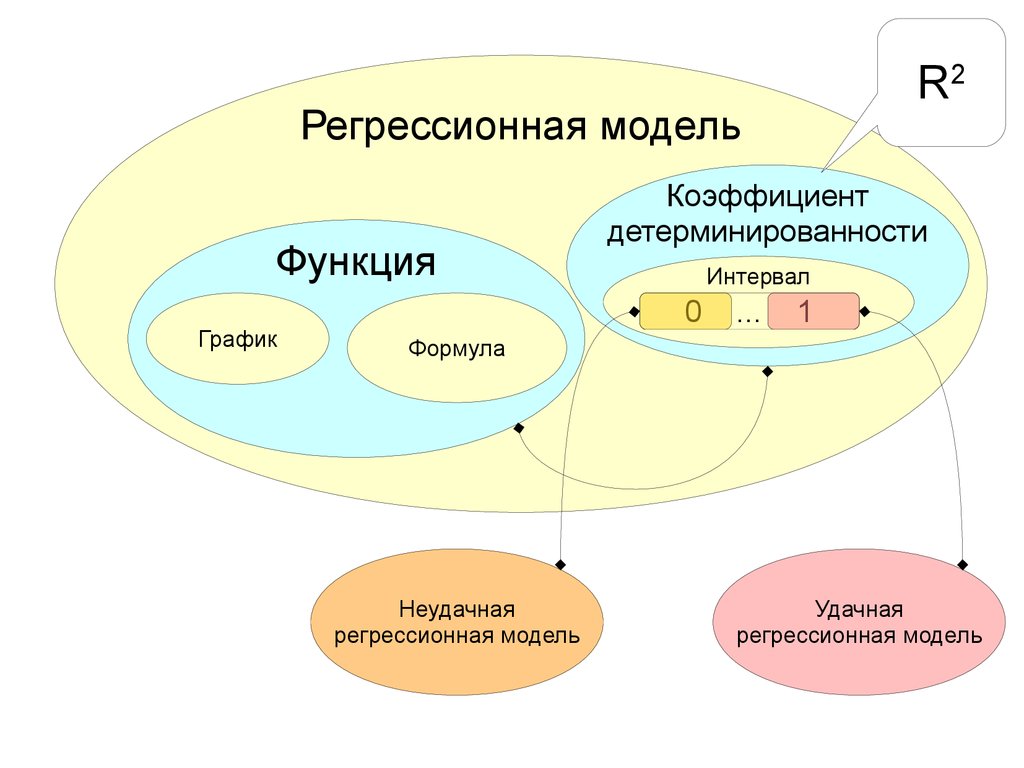
R2Регрессионная модель
Функция
График
Коэффициент
детерминированности
Интервал
0
...
1
Формула
Неудачная
регрессионная модель
Удачная
регрессионная модель
18.
Значения,полученные путём
измерений
В том числе
с помощью ЭТ
Регрессионная
математическая модель
В пределах
экспериментальных
значений
Прогнозирование процесса
для других значений аргумента
Восстановление
значения
За пределами
экспериментальных
данных
Экстраполяция
Графическим
способом
держится на
гипотезе:
предположим, что
за пределами
экспериментально
й области
закономерность
сохраняется
19.
ен
о
К
ф
ц
а
м
ь
л
и














 Математика
Математика








