Похожие презентации:
Решение плоской задачи наследственной теории старения методом конечных элементов
1.
IV СимпозиумАктуальные проблемы компьютерного моделирования
конструкций и сооружений
Г. Челябинск, 2012 год
РЕШЕНИЕ ПЛОСКОЙ ЗАДАЧИ
НАСЛЕДСТВЕННОЙ ТЕОРИИ СТАРЕНИЯ
МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Авторы: научный руководитель Гайджуров П.П.,
аспирантка
Исхакова Э.Р.
студент С-IV-1
Петросян П.Д.
Организация: Южно-Российский государственный
технический университет (НПИ), г. Новочеркасск
2.
ПроблемаВ настоящее время накоплен значительный экспериментальный и
теоретический материал по ползучести бетона. Вместе с тем
известные подходы к расчету бетонных и железобетонных
конструкций с учетом ползучести ориентированы главным образом
на решение задач с относительно простой геометрией изделия и при
неизменной внешней нагрузке. В литературе отсутствуют данные о
конечноэлементном моделировании напряженно-деформированного
состояния бетонных конструкций с учетом старения материала и
истории нагружения.
В работе J.T. Boyle и J. Spence приведен численный алгоритм
решения краевых задач ползучести (I и II стадии), основанный на
использовании уравнения состояния cr f ( , t , T ) , где σ –
напряжение, t – время, Т – температура . Данный подход не
учитывает изменение деформационных характеристик материала во
времени, не описывает обратной ползучести при разгрузке и
ориентирован на конструкции из металла и металлических сплавов.
Неявная схема численного интегрирования реализована ANSYSе.
3.
Цель исследованийРазработка и программная реализация алгоритма метода конечных
элементов для решения плоской задачи теории наследственного
старения с учетом переменного квазистатического нагружения,
позволяющего проектировать железобетонные конструкции на
стадии монтажа, включая технологию непрерывного
бетонирования, а также рассчитывать потерю предварительного
натяжения арматуры, обусловленную ползучестью бетона.
Направления исследований
Адаптация наследственных функций второго рода («функций
памяти»), предложенных Н.Х. Арутюняном
и С.В. Александровским, применительно к методу конечных
элементов в форме перемещений.
Построение конечноэлементного алгоритма и создание
соответствующего пакета программ для решения плоской задачи
теории наследственного старения.
4.
Наследственные функции II рода для бетонаОператорно-матричной форма физических соотношений
{ } [ E (t ) ] (1 R ){ } ,
где векторы напряжений и деформаций для плоской задачи
{ } { 11 2 2 12 } T , { } { 11 2 2 2 12 } T ,
[ E (t ) ] - матрица модулей упругости материала (3×3),
R (t , ) - ядро релаксации (наследственная функция II рода),
t
R i j R (t , ) i j ( ) d
- интегральный оператор,
τ – «возраст» материала в момент приложения нагрузки,
t – временная координата, отсчитываемая от момента времени τ.
Вид функции R (t , ) базируется на принятой механикоматематической модели ползучести бетона и применяемой
функции меры ползучести Ñ (t , ) .
5.
Теория старенияЯдро релаксации
t
E ( ) C ( , 1 ) d
1
R (t , )
E ( t ) e
E (t )
,
(1)
где функция меры ползучести Н.Х. Арутюняна
A1
[1 e ( t ) ]
Ñ (t , ) C 1
,
закон изменения модуля упругости материала
E ( t ) E 0 (1 e ) ,
C 1, A1 , , E 0 , - константы материала, определяемые
из опытов на ползучесть при одноосной деформации
Величину 1 принимаем равной 2 сут.
Достоинством представления наследственной функции в форме
(1) является то, что после обработки этого выражения в среде
символьного процессора системы Maple 12, получаем
следующую, легко программируемую формулу:
6.
R (t , )1 2 [ 1 (t ) ( ) 1 (t , ) 1 ( ) ( ) 2 (t , ) ] 3 (t , )
1
E
(
)
e
E (t )
E ( ) [ 3 2 3 (t , ) [ 1(t , ) 1( ) ( ) 2 (t , ) 2 ]
(2)
2 3 3 (t , )[ 1(t ) ( ) 1(t , ) 1( ) ( ) 2 (t , ) ] ]
,
1 2 3 (t , )[ 1(t ) ( ) 1(t , ) 1( ) ( ) 2 (t , ) ]
где введены обозначения:
E ( ) E 0 e ; 1 e
1 ( x) e
( x 1 )
1
1 ( )
; 1 (t , ) e
3 (t , ) e ( t) .
; 2 E 0 ( 1 C 1 A 1) ; 3
(t 1 )
; 2 ( t , ) e
( 1 ) t
;
1
;
1 ( )
7.
Теория наследственного старенияФункция меры ползучести С.В. Александровского
e A
2
C ( t , ) ( ) ( t )
( ) [1 e ( t ) ]
e t A
2
A3
.
Здесь обозначено: ( ) Ñ 3 ; ( ) C1 C 3
- опытные константы.
A1 , A 2 , A 3 , C 1, C 3, ,
(3)
A1 A 3
;
Выражение для ядра релаксации, полученное на основе
функции (3) имеет вид:
R (t , )
t
1
K 2 ( ) F ( ) (e A 2 ) K ( ) [ K ( ) (e A 2 )e ( ) ]
E (t )
K ( ) F ( ) e
( )
d B 3 (t ) e
(t ) (t )
,
(4)
8.
tE ( )
F ( )
; K ( )
; ( ) K ( ) F ( ) (e A 2 ) d ;
1 ( ) E ( )
e A2
1
( )
где
B 3 (t ) F (t ) (e t A 2 )[ E 2 (t ) K 2 (t ) ] E 2 (t ) K (t ) E (t ) ;
(t )
1
B 3 (t ) e t F (t )[ E 2 (t ) K 2 (t )] F 2 (t ) (e t A 2 ) 2
B 3 (t )
[ E 3 (t ) K 3 (t ) ] E (t )[ E (t ) (t ) ] 2 E 3 (t )
(t ) 1
F (t ) (e t A 2 )
K (t ) 2
[ E 2 (t ) K 2 (t )] 2 E 3 (t ) (t ) F (t ) (e t A 2 )
.
После обработки выражения (4) символьным процессором
системы Maple 12 и группировки членов получим следующую
формулу для наследственной функции:
E ( ) ( e A ) e
1
2
2
R (t , )
K ( ) F ( ) ( e A 2 ) K ( )
E (t )
1
(
)
E
(
)
( A1 A 3 ) E ( )
( )
E ( ) ( e A 2 ) e
1 ( ) E ( ) 2
( ) E ( )
2
E ( ) e e
(t ) ( t )
u ( ) B 3 (t ) e
,
1 ( ) E ( )
(5)
9.
tгде u ( ) K ( ) F ( ) e ( ) d ;
2 A3
2 A3 e t
3 ( t ) 2 e t 2 3 (t ) 2 e 2 t
1
(t ) B 3 (t )
3
t
2
t
2
t
2
t
3
(e A 2 )
( e A 2 )
t ( e A 2 ) t (e A 2 )
2
2
E 2 (t )
E 2 (t )
t
t
t
(e A 2 ) E (t )
F (t ) e E ( t )
F (t) (e A 2 )
1 (t )
1 (t )
2 (t )
E (t )
2
2 ( t ) E( t ) E (t )
2 E (t ) E (t ) 2 E ( t )
2 E ( )
2
3
1 (t )
1 (t)
2 ( A1 A 3 )
E (t)
t2
22 (t )
2
t
2 t
(t ) e
2 E(t ) 3 E 0 e
1 (t)
e F (t ) E 2 (t ) K 2 ( t ) F 2 ( t ) ( e t A 2 ) 2 E 3 ( t ) K 3 ( t )
E (t)
(t ) 1
E (t) (t ) E(t ) A1 A3 2 2 E3 (t)
F ( t) ( e t A 2 )
K (t ) 2
t
2 (t )
E (t )
2
3
t
2 E ( t) (t) F (t ) (e A 2 ) ;
2 E (t) E (t) E (t)
E (t )
12 (t)
13 (t)
1( ) 1 ( ) E ( ) ; 2 ( ) ( ) E ( )
( A1 A3 ) E ( )
2
; 3 ( ) C 3
A3
.
10.
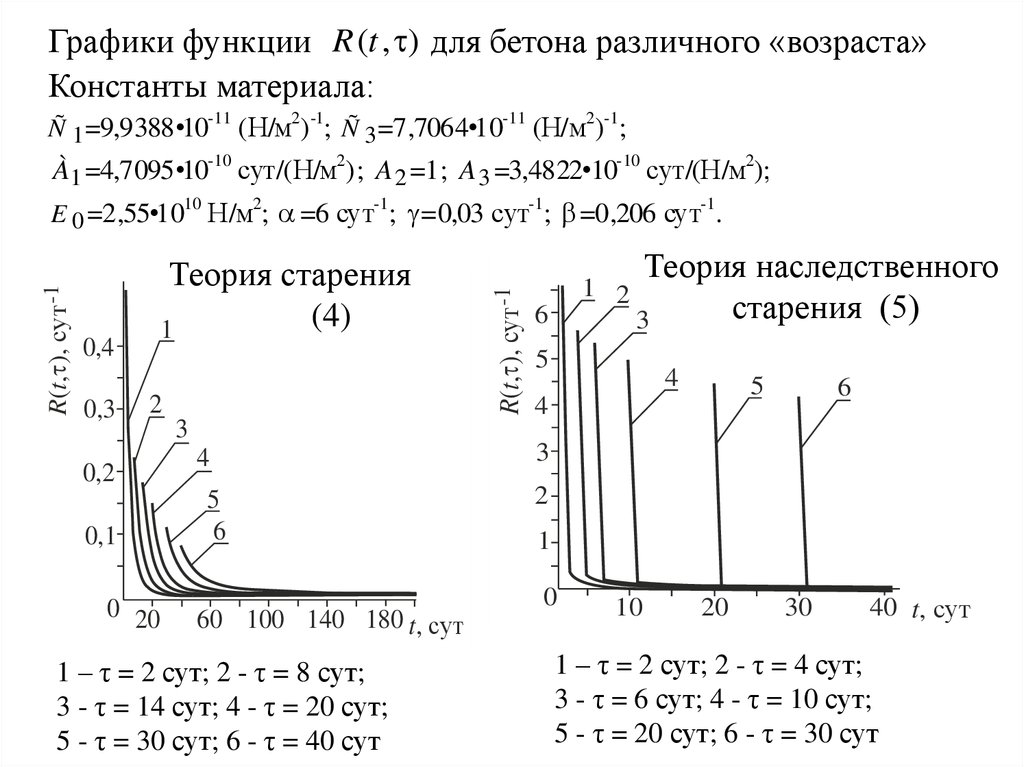
Графики функции R (t , ) для бетона различного «возраста»Константы материала:
-11
(Н/м2) -1; Ñ 3 =7,7064•10-11 (Н/м2)-1;
À1 =4,7095•10-10 сут/(Н/м2); A 2 =1; A 3 =3,4822•10-10 сут/(Н/м2);
Ñ 1 =9,9388•10
E 0 =2,55•10 Н/м ; =6 сут ; =0,03 сут ; =0,206 сут .
-1
Теория старения
(4)
1
0,4
0,3
2
2
0,2
0,1
0 20
3
4
5
6
60 100 140 180 t, сут
1 – τ = 2 сут; 2 - τ = 8 сут;
3 - τ = 14 сут; 4 - τ = 20 сут;
5 - τ = 30 сут; 6 - τ = 40 сут
-1
R(t, ), сут -1
R(t, ), сут -1
10
-1
1
6
Теория наследственного
2
старения (5)
3
5
4
5
4
6
3
2
1
0
10
20
30
40 t, сут
1 – τ = 2 сут; 2 - τ = 4 сут;
3 - τ = 6 сут; 4 - τ = 10 сут;
5 - τ = 20 сут; 6 - τ = 30 сут
11.
Конечноэлементная реализация плоской задачитеории ползучести
Векторы-столбцы наследственных деформаций и перемещений
{ } ( 1 R ){ } , {u } (1 R ){u} , { w} (1 R ){w} .
Отсюда
{u } (1 R ) [ F ]{ w} ,
где [ F ] - матрица, образованная из функций формы.
В соответствии с принципом возможных перемещений имеем
(6)
U
A 0,
где вариация энергии деформации
~ }T [ D ]T [ E ][ D ]{ w
~}d v ,
U {~ }T { }d v { w
ve
ve
возможная работа внешних сил
~ }T [ F ]{ q } d v { w
~ }T [ F ]{ p } d s .
A { w
ve
se
12.
Здесь обозначено: [ D ] - матрица, устанавливающая связь{ } [ D ] (1 R ) {w} ;
ve - объем, занимаемый КЭ;
s e -поверхность КЭ, к которой приложена
распределенная нагрузка;
{ q } { q 1 q 2 }T
- вектор-столбец объемной нагрузки;
{ p } { p 1 p 2 }T - вектор-столбец распределенной нагрузки.
Из уравнения (6) следует матричное соотношение
(7)
[ k ]{w} { r } 0 ,
T
[
k
]
[
D
]
[ E ][ D ] d v
где матрица жесткости КЭ
ve
T
T
и вектор-столбец узловых сил КЭ { r } [ F ] { q }d v [ F ] { p }d s .
ve
Подставляя в выражение (7) {w} получим
[ k ] (1 R ){w} { r } 0 .
se
(8)
13.
tДля вычисления интеграла R{w} R ( t , ){w ( )}d
воспользуемся численным методом, основанном на формуле
трапеций. Разобьем рассматриваемый временной интервал
[ , t ] на m равноотстоящих временных шагов t , так чтобы
t m t . Тогда, выражение (8) можно записать в форме
m 1
R {w m } R ( t , t ){w m } t / 2 R ( t , (m j ) t ) {w j } t
j 1
R ( t , ){w 1 } t / 2 { r } 0 .
Или в компактном виде
[ k m ]{ w m } { r } [ k 1 ]{ w1} [ k j ]{ w j } j 1, m 1 ,
(9)
где [ k m ] [ k ] (1 R (t , t ) t / 2 ; [ k 1 ] [ k ] (1 R ( t , ) t / 2 ;
[ k j ] [ k ] (1 R ( t , ( m j ) t ) t .
В выражении (9) вектор-столбец { w1 } соответствует упруго
мгновенному решению задачи.
14.
Числовые примерыq , МПа
Пример 1. Мгновенное нагружение и последующая
ступенчатая разгрузка призматического бетонного образца с
размерами 6×6×30 см (опыт А. Д. Росса ). “Возраст” бетона в
момент нагружения образца τ = 28 сут, момент времени
распалубки 1 = 2сут. Конечноэлементная разбивка 2×8 (2 КЭ
по ширине и 8 КЭ по высоте). Шаг интегрирования t = 1 сут.
15,2
11,4 7,6
3
v .10 , м
0
-2
3,8
q
1
1 – теория упругой
наследственности;
2 – теория старения;
3 – теория наследственного старения
2
-4
-6
20
3
60 100 140 180 t, сут
15.
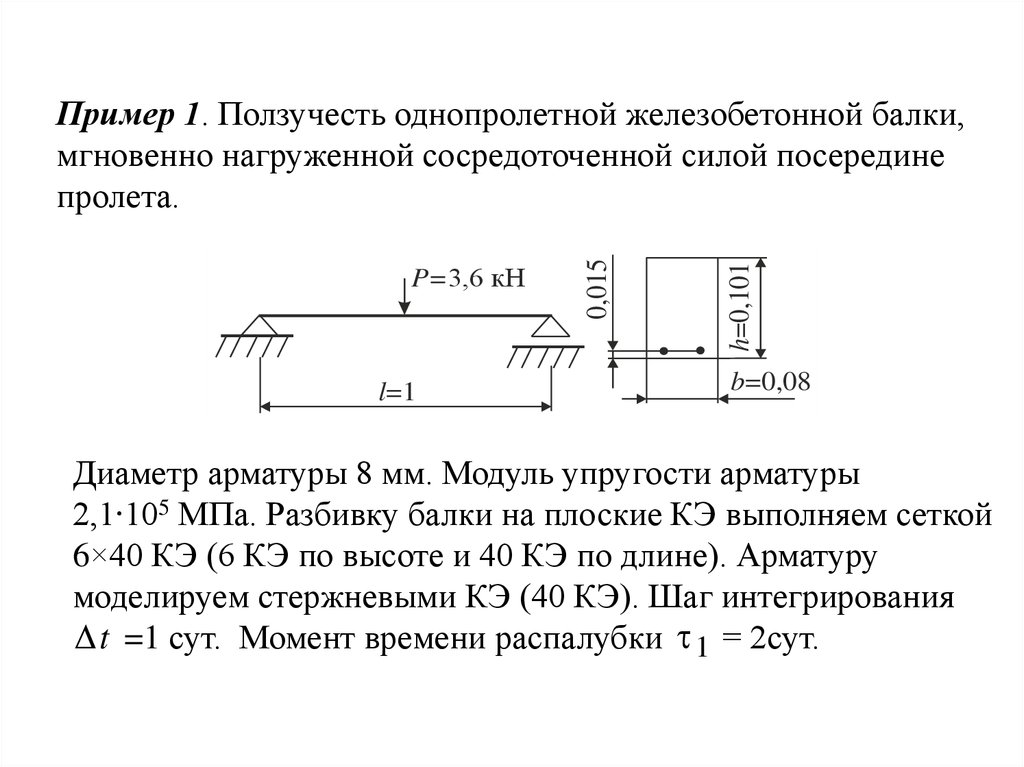
l=1h=0,101
P=3,6 кН
0,015
Пример 1. Ползучесть однопролетной железобетонной балки,
мгновенно нагруженной сосредоточенной силой посередине
пролета.
b=0,08
Диаметр арматуры 8 мм. Модуль упругости арматуры
2,1∙105 МПа. Разбивку балки на плоские КЭ выполняем сеткой
6×40 КЭ (6 КЭ по высоте и 40 КЭ по длине). Арматуру
моделируем стержневыми КЭ (40 КЭ). Шаг интегрирования
t =1 сут. Момент времени распалубки 1 = 2сут.
16.
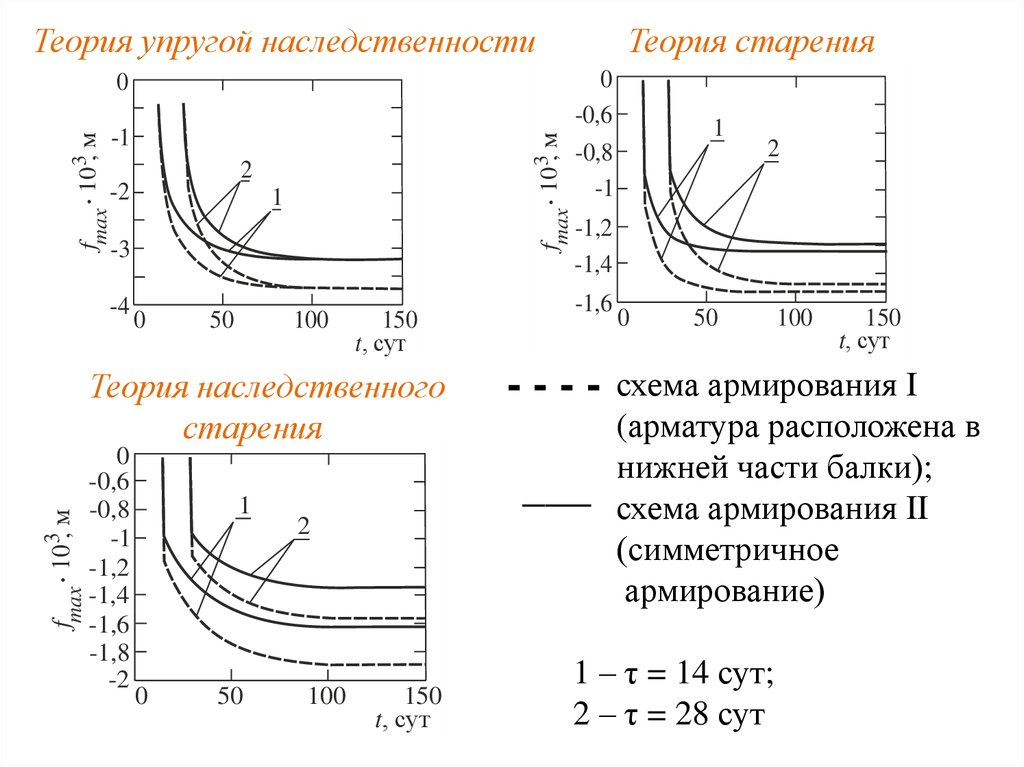
Теория упругой наследственности-1
fmax . 10 3, м
fmax . 10 3, м
0
2
-2
1
-3
-4
0
50
100
150
t, сут
fmax . 10 3, м
Теория наследственного
старения
0
-0,6
-0,8
-1
-1,2
-1,4
-1,6
-1,8
-2
1
0
50
Теория старения
0
-0,6
-0,8
-1
100
150
t, сут
2
-1,2
-1,4
-1,6
---___
2
1
0
50
100
150
t, сут
схема армирования I
(арматура расположена в
нижней части балки);
схема армирования II
(симметричное
армирование)
1 – τ = 14 сут;
2 – τ = 28 сут
17.
Выводы:1. В рамках теории старения и теории наследственного
старения с помощью символьного процессора системы
Maple 12 получены выражения для ядер релаксации
удобные для программирования.
2. Разработана и программно реализована шаговая процедура
метода конечных элементов, позволяющая моделировать
процессы последействия в бетонных и железобетонных
конструкциях с учетом старения бетона.
3. На тестовых примерах выполнена численная апробация
разработанной конечноэлементной программы.
18.
Благодарю за внимание!«… то что движется, есть материя.»
Г.Р. Кирхгоф





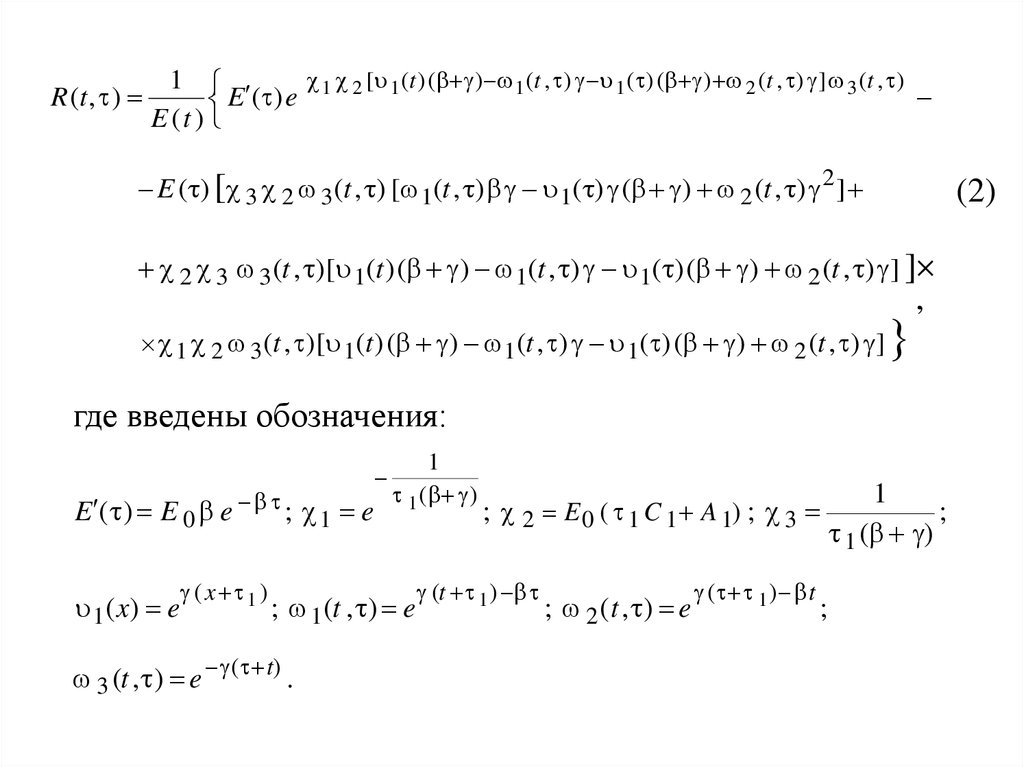









 Биология
Биология Программирование
Программирование








