Похожие презентации:
Показатели вариации. Задачи, решаемые при изучение вариации
1. Показатели вариации
2.
Вариация – этоизменения значений
признака во времени или
пространстве
3. Задачи, решаемые при изучение вариации:
1.Отражение дифференциации вариации впространстве.
2.Изменение вариации во времени.
3.Изучение специфических особенностей в
вариации отдельных частей целого .
4. Исследование вариации данного признака с
учетом его взаимосвязи с другими признаками.
4.
Показатели вариации1. Размах вариации
2. Среднее линейное отклонение
3. Дисперсия
4. Среднее квадратическое отклонение
5. Коэффициент вариации
5. Размах вариации
R Xmax minРазмах вариации
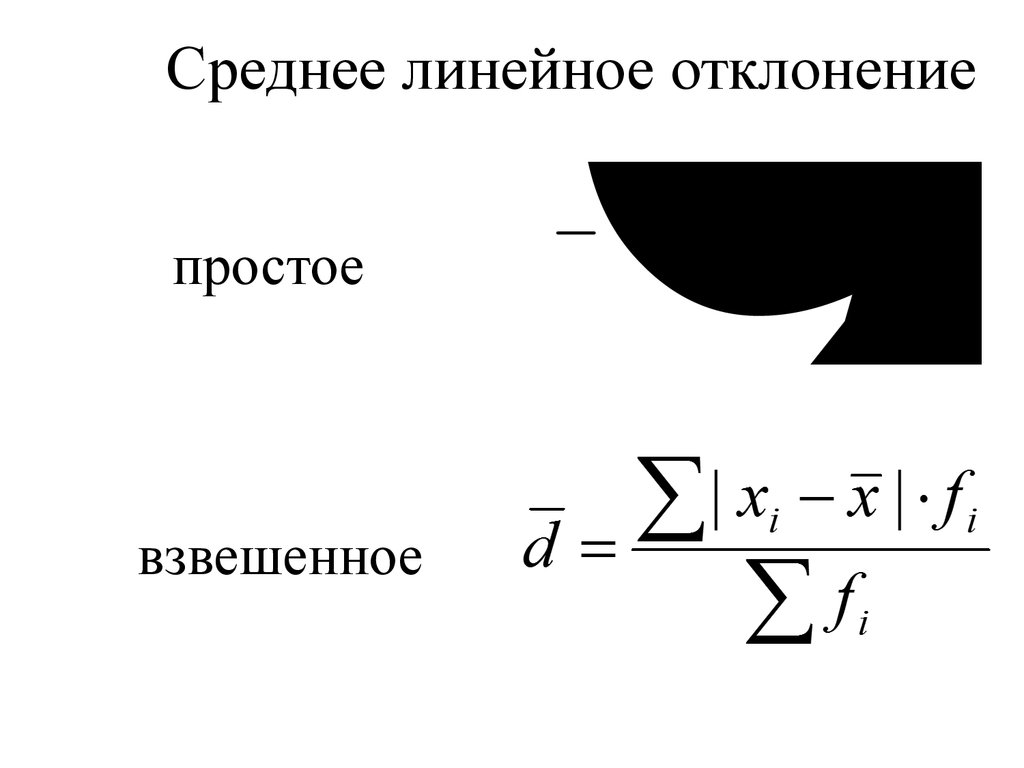
6. Среднее линейное отклонение
|d xn |i
Среднее линейное отклонение
простое
взвешенное
7. Дисперсия
(x
)
f
(
x
)
n2
2
2
x ()
2
2
2i 2iii
Дисперсия
простая
взвешенная
или
8. Среднее квадратическое отклонение
22
(
x
)
i
n
2
( xi i) fi
Среднее квадратическое
отклонение
простое
взвешенное
9. Линейный коэффициент вариации
dV 100
x
10. Коэффициент вариации
Vx 10
Коэффициент вариации
11. Пример:
Имеется распределение семей почислу детей
Группы семей по
числу детей, чел
Число семей
0
1
2
3
4
10
20
30
17
3
Всего
80
12. Решение:
2 fi|R
x
|4
i
f0
(
x4
)iч
xxi 18f40i3 x, 8fix
ел
Решение:
0
1
2
3
4
10
20
30
17
3
0
20
60
51
12
-1,8
-0,8
0,2
1,2
2,2
18
16
6
20,4
6,6
32,4
12,8
1,2
24,5
14,5
Всего 80
143
-
67
85,4
13.
67
dV
,
0
8
4
8
5
2
1
0
7
2
, x 0 1,0830 3 57,2%
1
14. Виды дисперсий и правило их сложения.
15. Виды дисперсий
• Общая дисперсия• внутригрупповые дисперсии
• межгрупповая дисперсия
16. Общая дисперсия
(f
x
)
2
2iii
Общая дисперсия
17.
Общая дисперсия измеряет вариациюпризнака во всей совокупности под
влиянием всех факторов
18. Внутригрупповая дисперсия
(n
x
)
2
2
i
i
i
i
Внутригрупповая дисперсия
19.
Внутригрупповая дисперсия, отражаетслучайную вариацию, т.е. ту часть
вариации, которая складывается под
влиянием неучтенных фактов и
независящую от признака-фактора
20. Средняя из внутригрупповых дисперсий
n2
2
i
i
i
Средняя из внутригрупповых дисперсий
21. Межгрупповая дисперсия
( x ) n2
2iii
Межгрупповая дисперсия
22.
Межгрупповая дисперсия характеризуетсистематическую вариацию, т.е. различия в
величине изучаемого признака,
возникающие под воздействием признакафактора положенного в основание
группировки
23. Правило сложения дисперсий
222Правило сложения дисперсий
24. Эмпирический коэффициент детерминации
22
Эмпирический коэффициент
детерминации
25.
Этот коэффициент представляет собой долюмежгрупповой дисперсии в общей
дисперсии изучаемого признака
Показывает удельный вес общей вариации
изучаемого признака, обусловленную
вариацией группировочного признака.
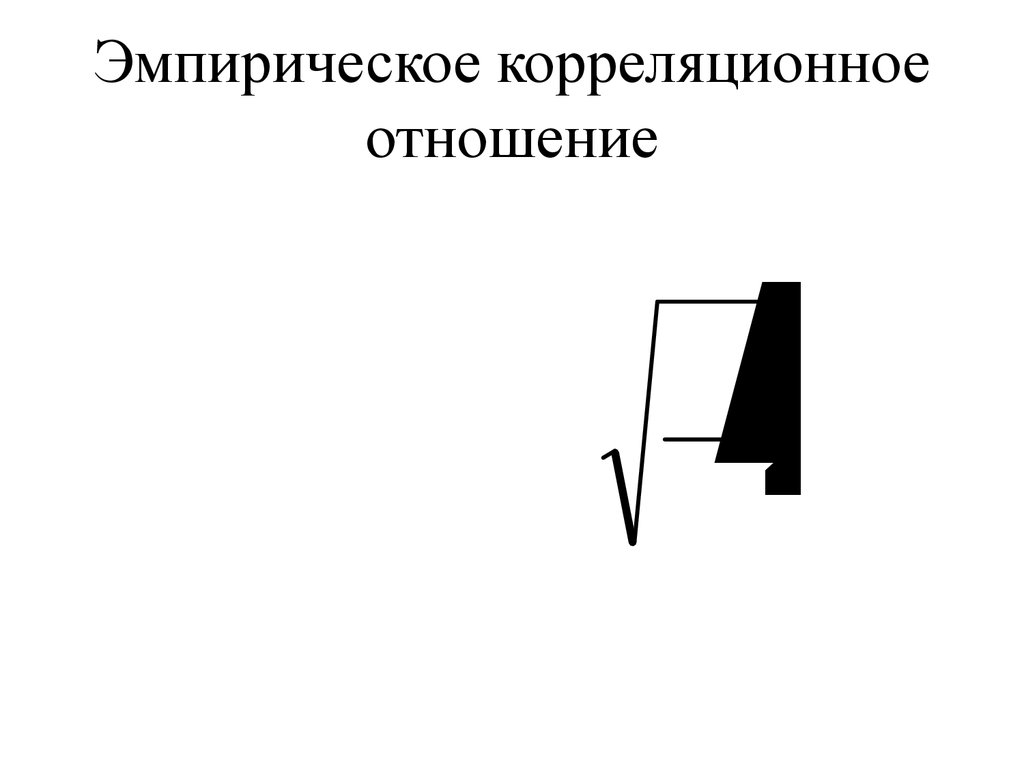
26. Эмпирическое корреляционное отношение
2Эмпирическое корреляционное
отношение
27.
Он характеризует влияние признака,положенного в основание группировки, на
вариацию результативного признака, с его
помощью оценивают тесноту связи между
признаками.
28.
Если , равен 1 то результативный признакизменяется только в зависимости от
признака, положенного в основании
группировки, а влияние прочих
факторных признаков равно нулю.
Если , равен 0 то группировочный признак
не оказывает влияние на результативный.
Промежуточные значения оцениваются в
зависимости от их близости к
предельным значениям.
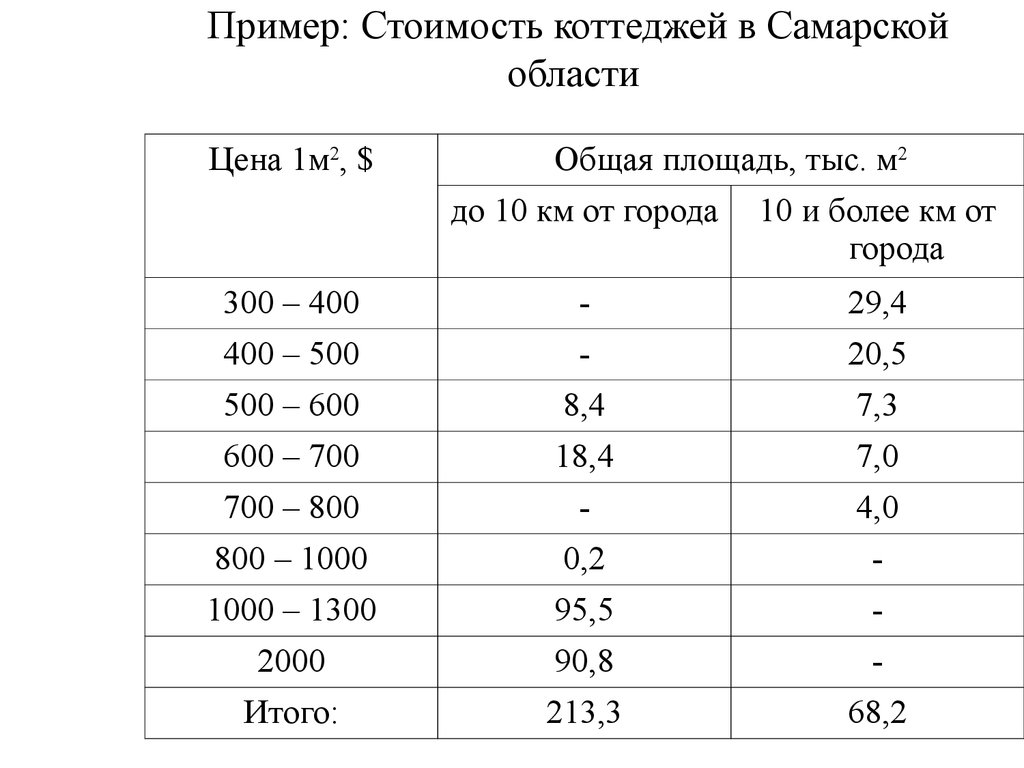
29. Пример: Стоимость коттеджей в Самарской области
Цена 1м2, $Общая площадь, тыс. м2
до 10 км от города
10 и более км от
города
300 – 400
400 – 500
-
29,4
20,5
500 – 600
600 – 700
700 – 800
800 – 1000
8,4
18,4
0,2
7,3
7,0
4,0
-
1000 – 1300
2000
Итого:
95,5
90,8
213,3
68,2
30. 1. Определяем объем каждой группы
31. 2. Рассчитываем среднее значение цены для каждой группы
32. 3. Рассчитаем внутригрупповые дисперсии
21 256431
2
2 14733
33. 4. Рассчитываем среднюю из внутригрупповых дисперсий
2256431* 213.3 14733 * 68.2
197874
213.3 68.2
34. 5. Определяем межгрупповую дисперсию
1795612
35. Общая дисперсия
2o 197874 179561 377435
36. Корреляционное отношение
1795610.69
377435

































 Математика
Математика








