Трёхгранный угол

1.

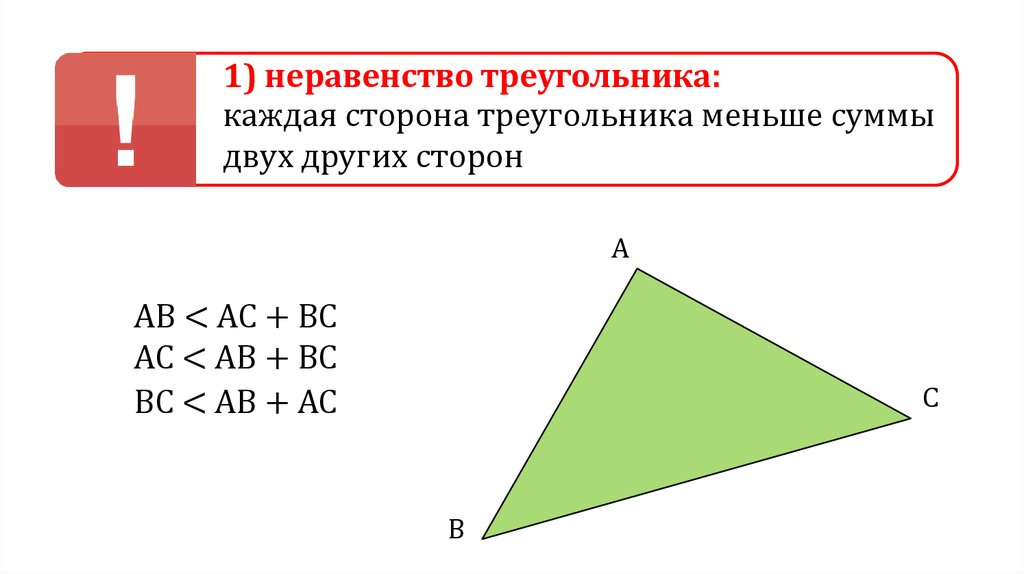
1) неравенство треугольника:
каждая сторона треугольника меньше суммы
двух других сторон
А
AB < AC + BC
AC < AB + BC
BC < AB + AC
С
B

2.

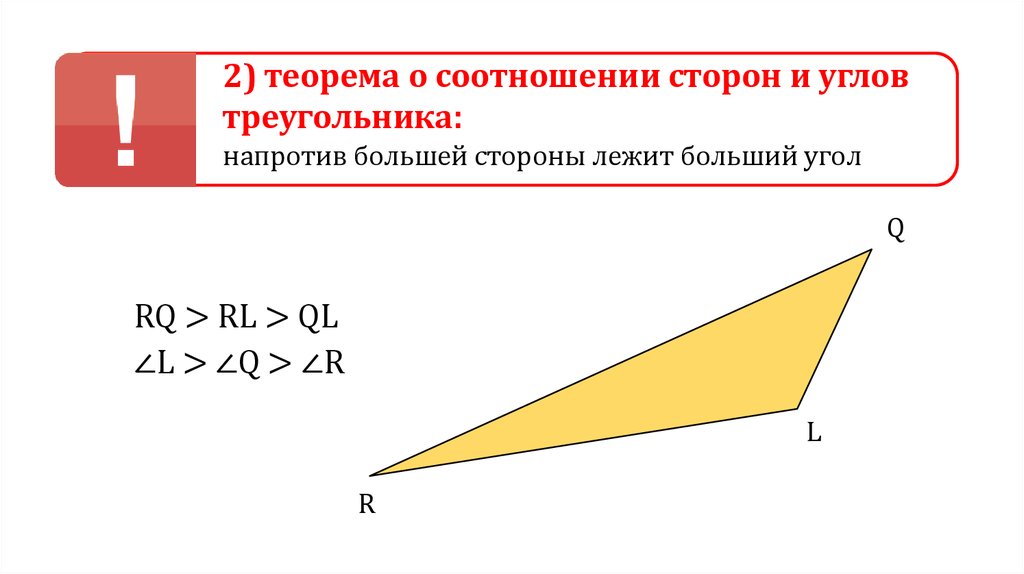
2) теорема о соотношении сторон и углов
треугольника:
напротив большей стороны лежит больший угол
Q
RQ > RL > QL
∠L > ∠Q > ∠R
L
R

3.

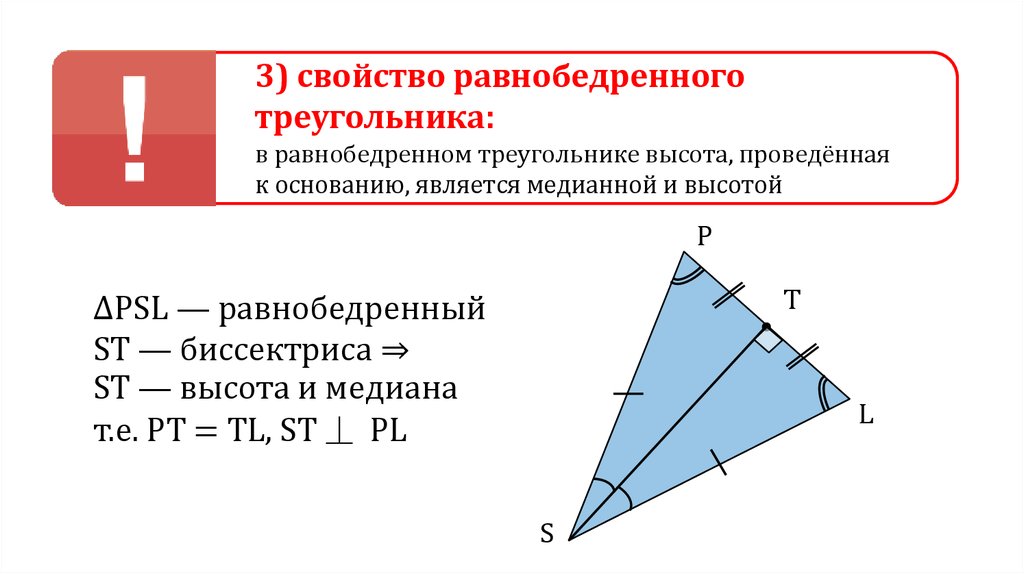
3) свойство равнобедренного
треугольника:
в равнобедренном треугольнике высота, проведённая
к основанию, является медианной и высотой
P
T
∆PSL — равнобедренный
ST — биссектриса ⇒
ST — высота и медиана
т.е. PT = TL, ST ⏊ PL
L
S

4.

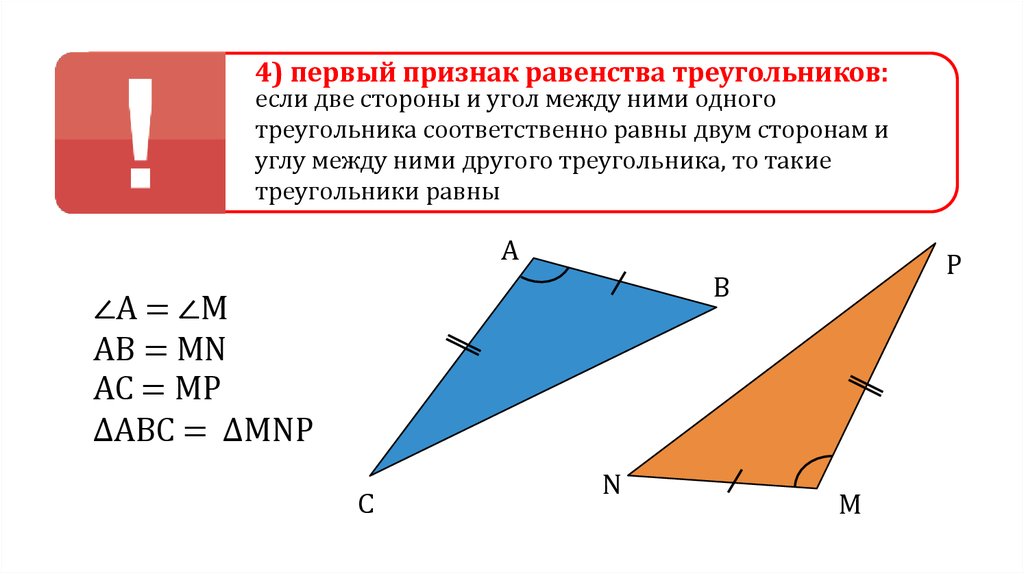
4) первый признак равенства треугольников:
если две стороны и угол между ними одного
треугольника соответственно равны двум сторонам и
углу между ними другого треугольника, то такие
треугольники равны
A
P
B
∠А = ∠М
AB = MN
AC = MP
∆ABC = ∆MNP
C
N
M

5.

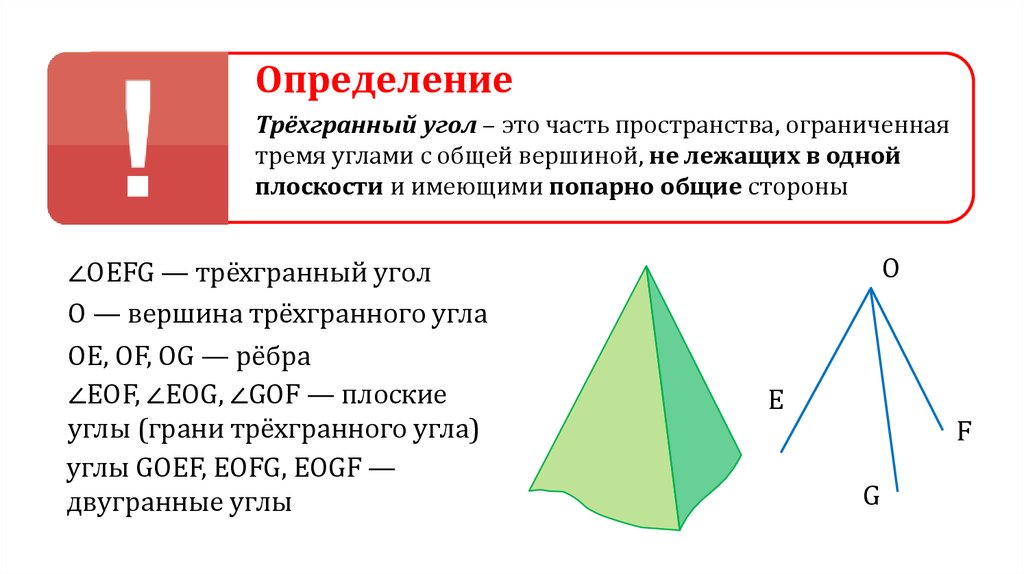
Определение
Трёхгранный угол – это часть пространства, ограниченная
тремя углами с общей вершиной, не лежащих в одной
плоскости и имеющими попарно общие стороны
∠OEFG — трёхгранный угол
О — вершина трёхгранного угла
OE, OF, OG — рёбра
∠EOF, ∠EOG, ∠GOF — плоские
углы (грани трёхгранного угла)
углы GOEF, EOFG, EOGF —
двугранные углы
O
E
F
G

6.

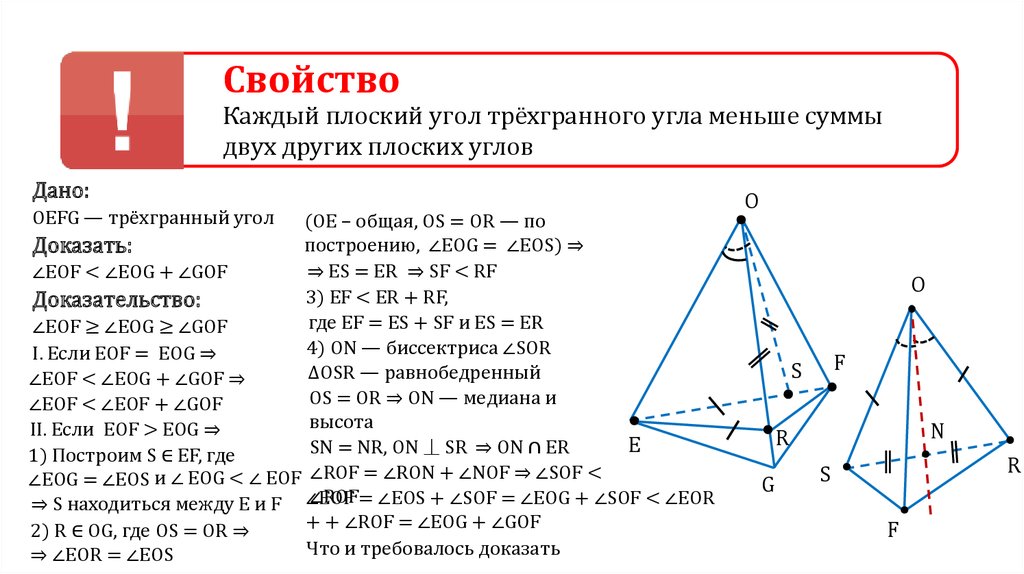
Свойство
Каждый плоский угол трёхгранного угла меньше суммы
двух других плоских углов
Дано:
OEFG — трёхгранный угол
(OE – общая, OS = OR — по
построению, ∠EOG = ∠EOS) ⇒
Доказать:
⇒ ES = ER ⇒ SF < RF
∠EOF < ∠EOG + ∠GOF
3) EF < ER + RF,
Доказательство:
где EF = ES + SF и ES = ER
∠EOF ≥ ∠EOG ≥ ∠GOF
4) ON — биссектриса ∠SOR
I. Если EOF = EOG ⇒
∆OSR — равнобедренный
∠EOF < ∠EOG + ∠GOF ⇒
OS = OR ⇒ ON — медиана и
∠EOF < ∠EOF + ∠GOF
высота
II. Если EOF > EOG ⇒
E
SN = NR, ON ⏊ SR ⇒ ON ∩ ER
1) Построим S ∈ EF, где
∠EOG = ∠EOS и ∠ EOG < ∠ EOF ∠ROF = ∠RON + ∠NOF ⇒ ∠SOF <
∠ROF= ∠EOS + ∠SOF = ∠EOG + ∠SOF < ∠EOR
⇒ S находиться между E и F ∠EOF
+ + ∠ROF = ∠EOG + ∠GOF
2) R ∈ OG, где OS = OR ⇒
Что и требовалось доказать
⇒ ∠EOR = ∠EOS
O
O
F
S
N
R
G
R
S
F

7.

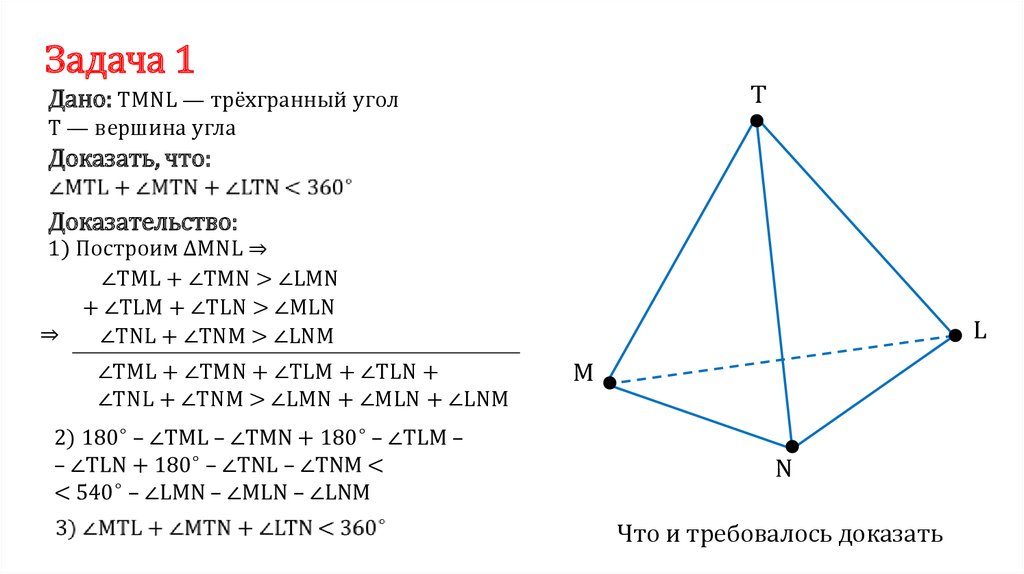
Задача 1
T
Дано: TMNL — трёхгранный угол
T — вершина угла
Доказать, что:
Доказательство:
1) Построим ∆MNL ⇒
∠TML + ∠TMN > ∠LMN
+ ∠TLM + ∠TLN > ∠MLN
⇒
∠TNL + ∠TNM > ∠LNM
∠TML + ∠TMN + ∠TLM + ∠TLN +
∠TNL + ∠TNM > ∠LMN + ∠MLN + ∠LNM
L
M
N
Что и требовалось доказать