Похожие презентации:
Понятие. Характеристики понятий
1. ПОНЯТИЕ
Понятие – это мысль, которая посредством указанияна некоторый признак выделяет из некоторого
универсума (области рассмотрения) и собирает в
класс (обобщает) предметы, обладающие этим
признаком (все такие и только их).
Примеры выражения понятий в языке
Предмет мебели, предназначенный для сидения (СТУЛ)
Геометрическое тело, образованное вращением прямоугольного
треугольника вокруг одного из его катетов (КОНУС)
Государство, возглавляемое, как правило, пожизненно, одним
человеком, получающим это право по наследству (МОНАРХИЯ)
2. ХАРАКТЕРИСТИКИ ПОНЯТИЙ
Прежде всего, это объем и содержаниеОбъем понятия – это само множество предметов,
выделяемых из универсума и обобщаемых в
данном понятии.
Это экстенсиональная характеристика.
Содержание понятия – это признак, на
основании которого в понятии осуществляется
операция обобщения.
Это интенсиональная характеристика.
3. ХАРАКТЕРИСТИКИ ПОНЯТИЙ
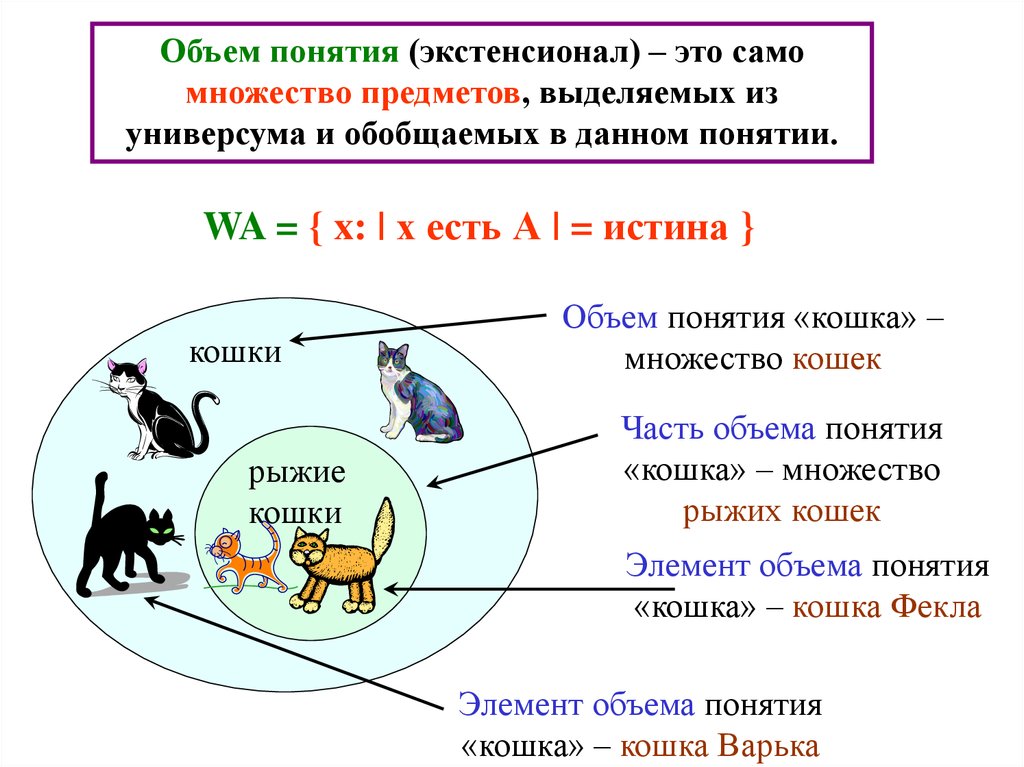
Объем понятия (экстенсионал) – это самомножество предметов, выделяемых из
универсума и обобщаемых в данном понятии.
Содержание понятия (интенсионал) – это
признак, на основании которого в понятии
осуществляется операция обобщения.
Очевидно, что два понятия могут иметь одинаковый объем,
но разное содержание.
Геометрическая фигура, являющаяся равноугольным ромбом
(КВАДРАТ)
Геометрическая фигура, являющаяся равносторонним
прямоугольником (КВАДРАТ)
4. ХАРАКТЕРИСТИКИ ПОНЯТИЙ
Объем понятия (экстенсионал) – это самомножество предметов, выделяемых из
универсума и обобщаемых в данном понятии.
Содержание понятия (интенсионал) – это
признак, на основании которого в понятии
осуществляется операция обобщения.
Очевидно, что два понятия могут иметь одинаковый объем,
но разное содержание.
Писатель, автор «Анны Карениной» (Лев Толстой)
Писатель, автор «Войны и мира» (Лев Толстой)
5.
Объем понятия (экстенсионал) – это самомножество предметов, выделяемых из
универсума и обобщаемых в данном понятии.
WA = { x: | х есть А | = истина }
кошки
рыжие
кошки
Объем понятия «кошка» –
множество кошек
Часть объема понятия
«кошка» – множество
рыжих кошек
Элемент объема понятия
«кошка» – кошка Фекла
Элемент объема понятия
«кошка» – кошка Варька
6. ЗАКОН ОБРАТНОГО ОТНОШЕНИЯ МЕЖДУ ОБЪЕМАМИ И СОДЕРЖАНИЯМИ ПОНЯТИЙ
Понятие А ýже по объему, чем понятие В(объем А есть собственная часть объема В),
тогда и только тогда, когда
А богаче по содержанию, чем В.
WA WB I (A) ╞ I (B), но I (B) ╞ I (A)
WA – объем понятия А
I (A) – информация, заключенная в содержании А
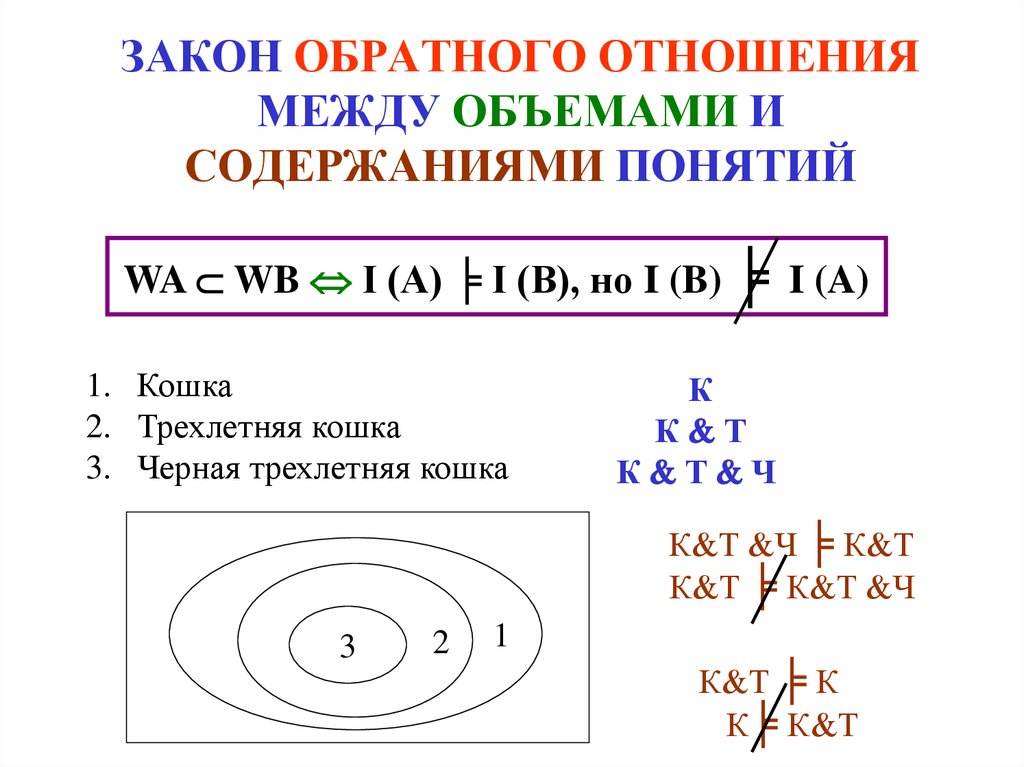
7. ЗАКОН ОБРАТНОГО ОТНОШЕНИЯ МЕЖДУ ОБЪЕМАМИ И СОДЕРЖАНИЯМИ ПОНЯТИЙ
WA WB I (A) ╞ I (B), но I (B) ╞ I (A)1. Кошка
2. Трехлетняя кошка
3. Черная трехлетняя кошка
К
К Т
К Т Ч
К Т Ч ╞ К Т
К Т ╞ К Т Ч
3
2
1
К Т ╞ К
К╞ К Т
8. ЗАКОН ОБРАТНОГО ОТНОШЕНИЯ МЕЖДУ ОБЪЕМАМИ И СОДЕРЖАНИЯМИ ПОНЯТИЙ
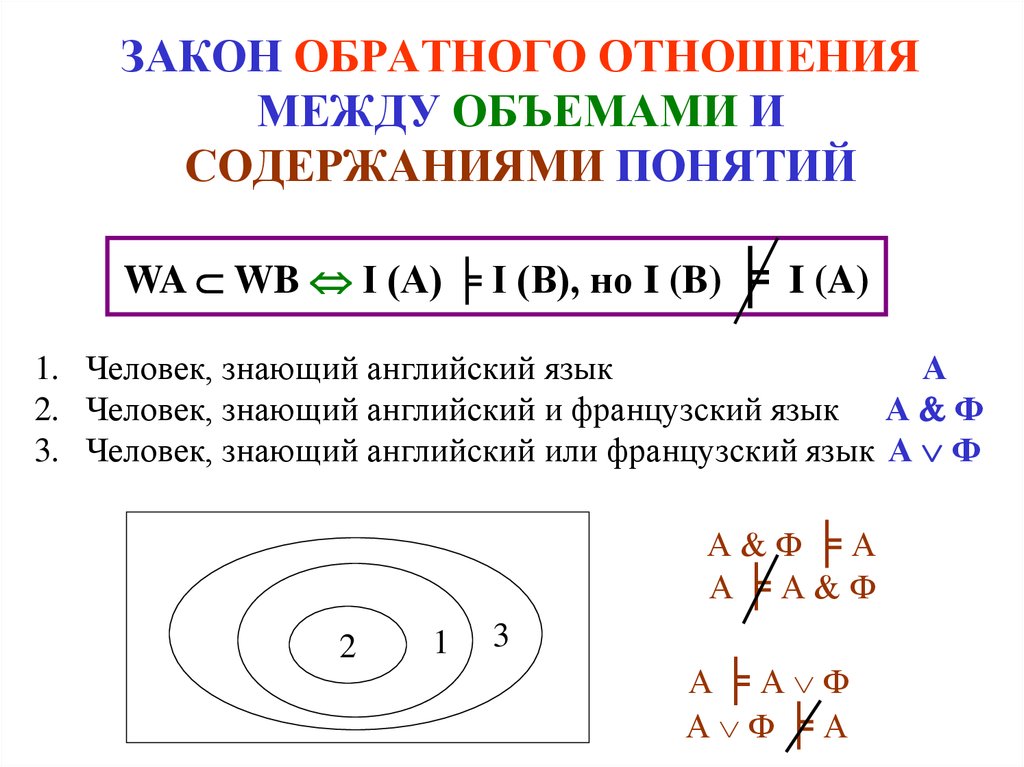
WA WB I (A) ╞ I (B), но I (B) ╞ I (A)1. Человек, знающий английский язык
А
2. Человек, знающий английский и французский язык А Ф
3. Человек, знающий английский или французский язык А Ф
А Ф╞А
А╞А Ф
2
1
3
А╞А Ф
А Ф╞А
9. ЗАКОН ОБРАТНОГО ОТНОШЕНИЯ МЕЖДУ ОБЪЕМАМИ И СОДЕРЖАНИЯМИ ПОНЯТИЙ
WA WB I (A) ╞ I (B), но I (B) ╞ I (A)1. Человек, сдавший некоторые экзамены в эту сессию Некот. x
2. Человек, сдавший логику в эту сессию
Конкретное a
3. Человек, сдавший все экзамены в эту сессию
Все х
Все ╞ Конкретный
Конкретный ╞ Все
3
2
1
Конкретный ╞ Некоторые
Некоторые ╞ конкретный
10. ЗАКОН ОБРАТНОГО ОТНОШЕНИЯ
WA WB I (A) ╞ I (B), но I (B) ╞ I (A)1.
2.
3.
4.
5.
6.
7.
Человек, знающий все европейские языки
Человек, знающий все живые европейские языки
Человек, знающий английский язык
Человек, знающий английский и французский язык
Человек, знающий английский или французский язык
Человек, знающий некоторые европейские языки
Человек, знающий некоторые живые европейские языки
1╞ 2 ╞ 4 ╞ 3 ╞ 5 ╞ 7╞ 6
1
2 4 3 5 7
6
(но не наоборот)
11. КЛАССИФИКАЦИИ ПОНЯТИЙ
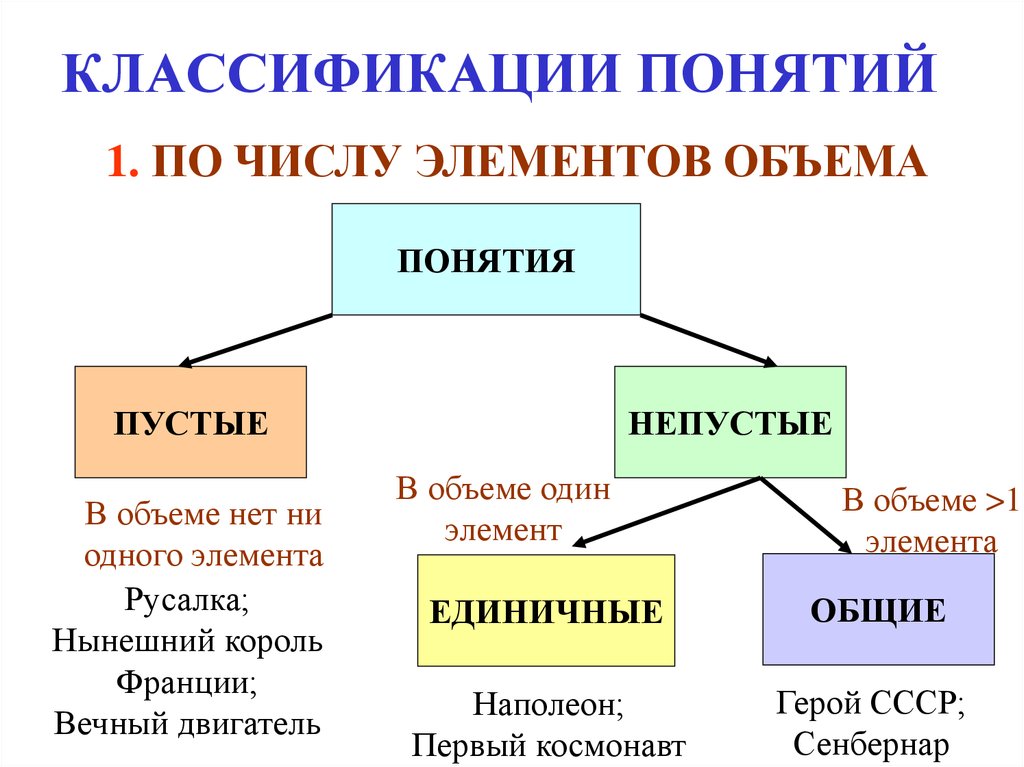
1. ПО ЧИСЛУ ЭЛЕМЕНТОВ ОБЪЕМАПОНЯТИЯ
ПУСТЫЕ
В объеме нет ни
одного элемента
Русалка;
Нынешний король
Франции;
Вечный двигатель
НЕПУСТЫЕ
В объеме один
элемент
В объеме >1
элемента
ЕДИНИЧНЫЕ
ОБЩИЕ
Наполеон;
Первый космонавт
Герой СССР;
Сенбернар
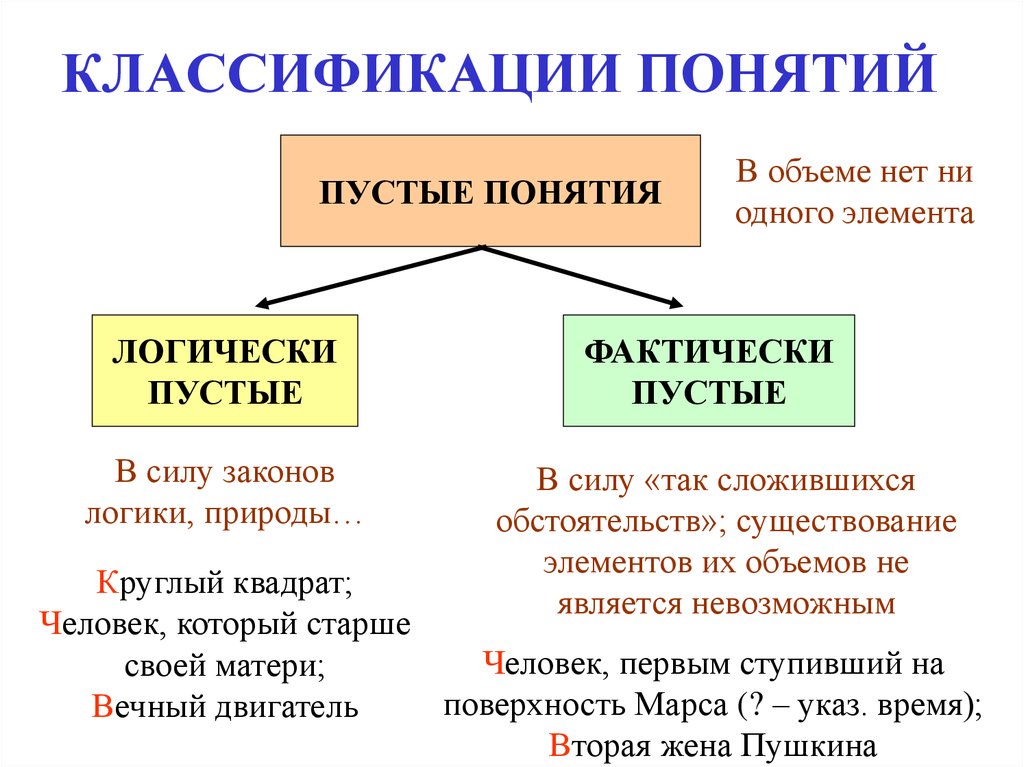
12. КЛАССИФИКАЦИИ ПОНЯТИЙ
ПУСТЫЕ ПОНЯТИЯЛОГИЧЕСКИ
ПУСТЫЕ
В силу законов
логики, природы…
В объеме нет ни
одного элемента
ФАКТИЧЕСКИ
ПУСТЫЕ
В силу «так сложившихся
обстоятельств»; существование
элементов их объемов не
является невозможным
Круглый квадрат;
Человек, который старше
Человек, первым ступивший на
своей матери;
поверхность Марса (? – указ. время);
Вечный двигатель
Вторая жена Пушкина
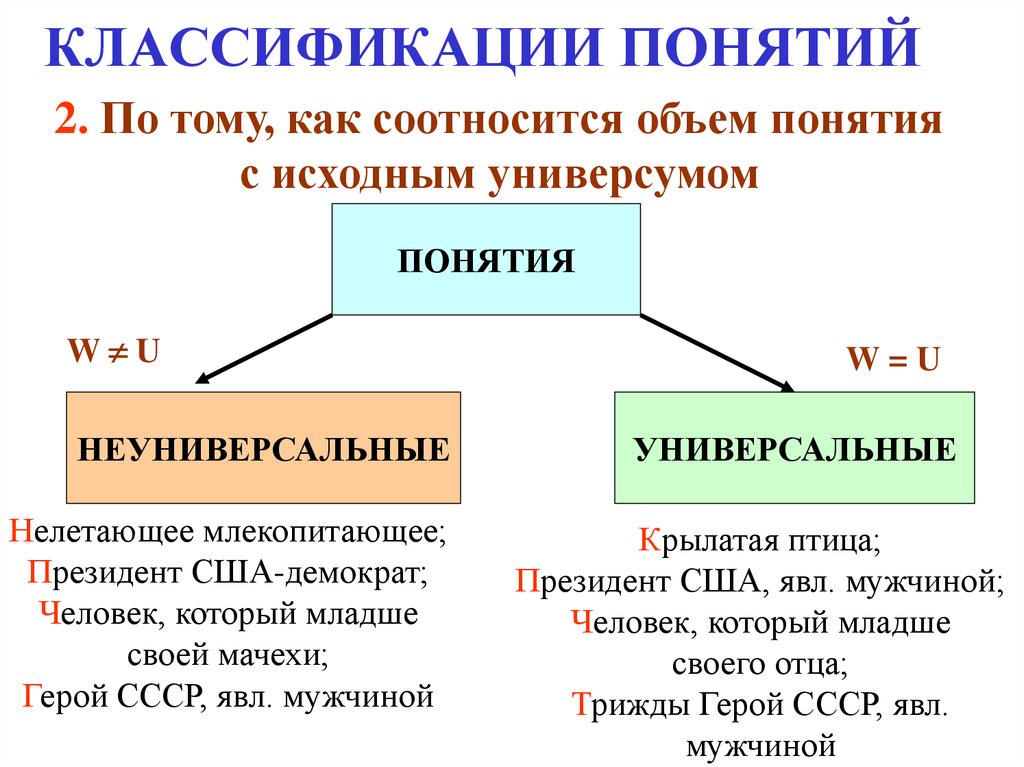
13. КЛАССИФИКАЦИИ ПОНЯТИЙ
2. По тому, как соотносится объем понятияс исходным универсумом
ПОНЯТИЯ
W U
НЕУНИВЕРСАЛЬНЫЕ
Нелетающее млекопитающее;
Президент США-демократ;
Человек, который младше
своей мачехи;
Герой СССР, явл. мужчиной
W=U
УНИВЕРСАЛЬНЫЕ
Крылатая птица;
Президент США, явл. мужчиной;
Человек, который младше
своего отца;
Трижды Герой СССР, явл.
мужчиной
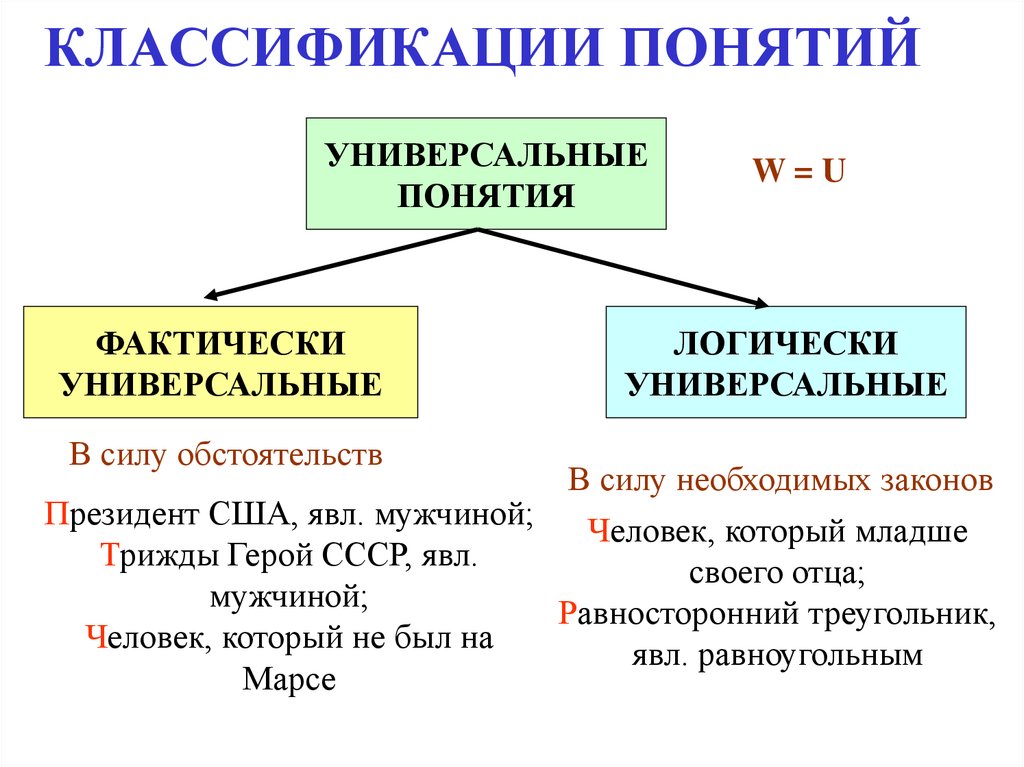
14. КЛАССИФИКАЦИИ ПОНЯТИЙ
УНИВЕРСАЛЬНЫЕПОНЯТИЯ
ФАКТИЧЕСКИ
УНИВЕРСАЛЬНЫЕ
В силу обстоятельств
W=U
ЛОГИЧЕСКИ
УНИВЕРСАЛЬНЫЕ
В силу необходимых законов
Президент США, явл. мужчиной;
Человек, который младше
Трижды Герой СССР, явл.
своего отца;
мужчиной;
Равносторонний треугольник,
Человек, который не был на
явл. равноугольным
Марсе
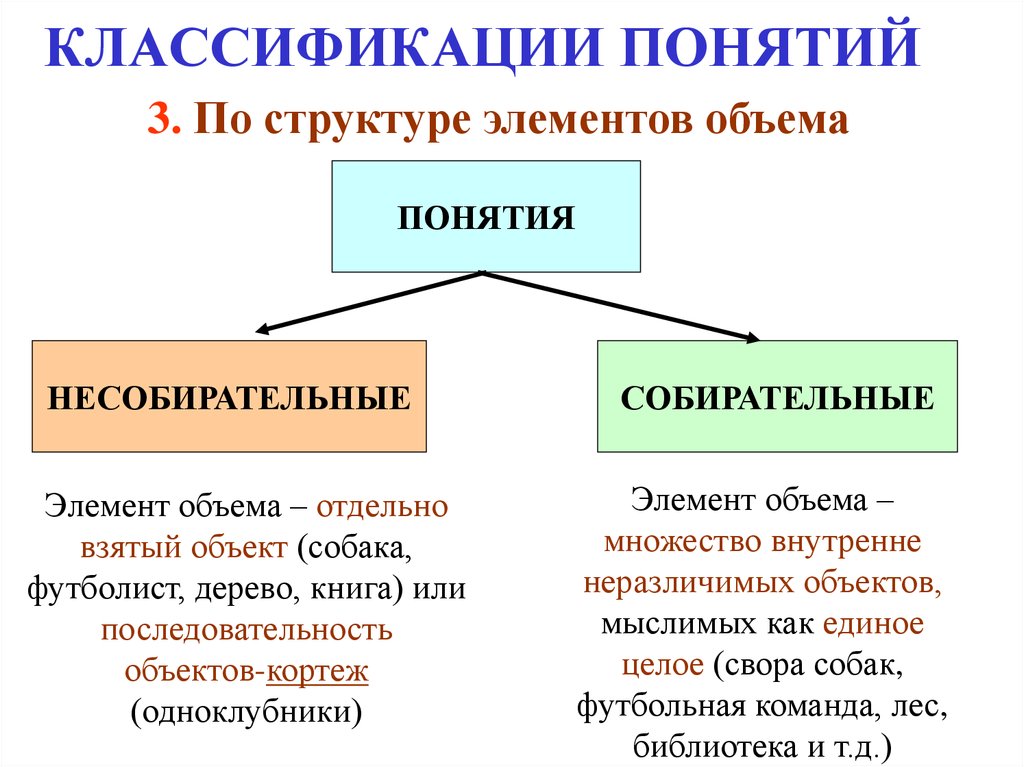
15. КЛАССИФИКАЦИИ ПОНЯТИЙ
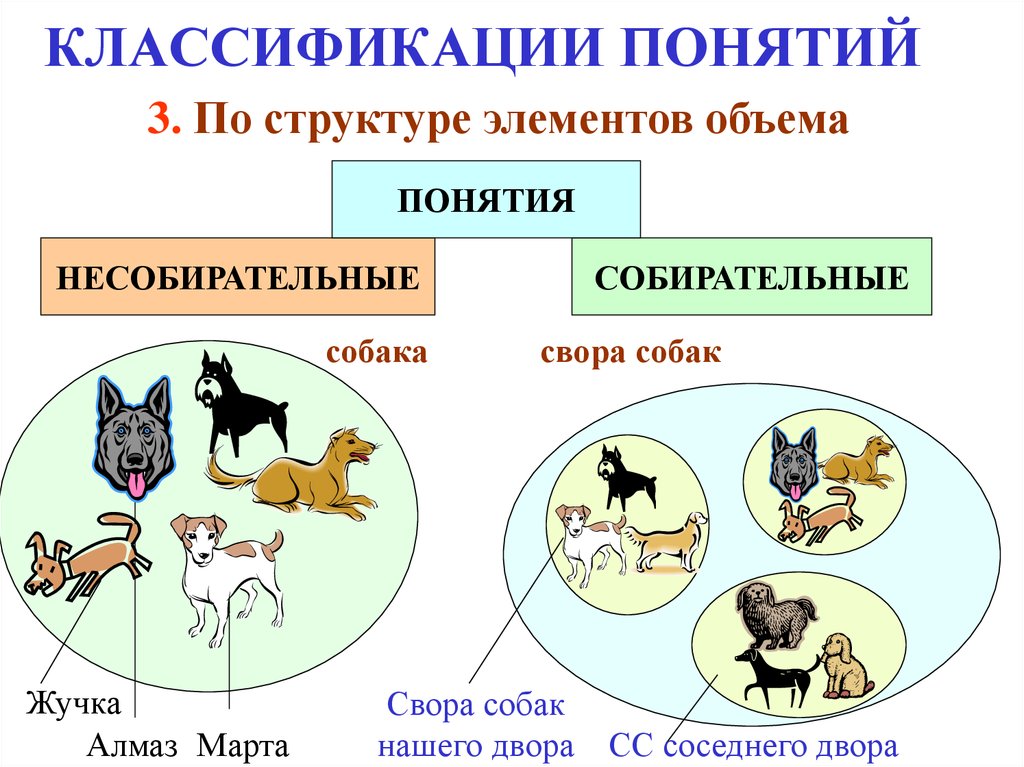
3. По структуре элементов объемаПОНЯТИЯ
НЕСОБИРАТЕЛЬНЫЕ
Элемент объема – отдельно
взятый объект (собака,
футболист, дерево, книга) или
последовательность
объектов-кортеж
(одноклубники)
СОБИРАТЕЛЬНЫЕ
Элемент объема –
множество внутренне
неразличимых объектов,
мыслимых как единое
целое (свора собак,
футбольная команда, лес,
библиотека и т.д.)
16. КЛАССИФИКАЦИИ ПОНЯТИЙ
3. По структуре элементов объемаПОНЯТИЯ
НЕСОБИРАТЕЛЬНЫЕ
собака
Жучка
Алмаз Марта
СОБИРАТЕЛЬНЫЕ
свора собак
Свора собак
нашего двора СС соседнего двора
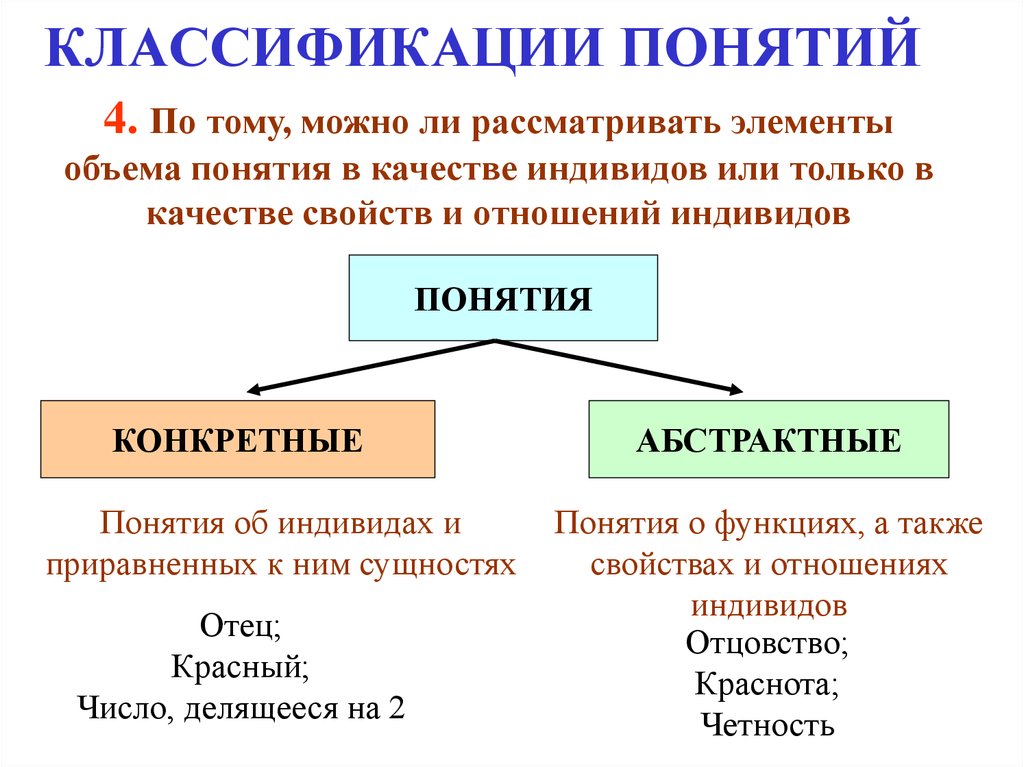
17. КЛАССИФИКАЦИИ ПОНЯТИЙ
4. По тому, можно ли рассматривать элементыобъема понятия в качестве индивидов или только в
качестве свойств и отношений индивидов
ПОНЯТИЯ
КОНКРЕТНЫЕ
Понятия об индивидах и
приравненных к ним сущностях
Отец;
Красный;
Число, делящееся на 2
АБСТРАКТНЫЕ
Понятия о функциях, а также
свойствах и отношениях
индивидов
Отцовство;
Краснота;
Четность
18. ЛОГИЧЕСКИЕ ОПЕРАЦИИ НАД ПОНЯТИЯМИ
Классы операцийI. Обобщение и ограничение.
II. Булевы операции над объемами понятий
(дополнение, объединение, пересечение,
вычитание).
III.Деление (ступенчатая система делений –
классификация).
19. I. ОБОБЩЕНИЕ И ОГРАНИЧЕНИЕ
Обобщение (понятия А) –это переход (от понятия А) к такому понятию В,
что WA WB.
Ограничение (понятия А) –
это переход (от понятия А) к такому непустому
понятию В, что WВ WА.
20.
Обобщение (понятия А) –это переход (от понятия А) к такому понятию В,
что WA WB.
Ограничение (понятия А) –
это переход (от понятия А) к такому непустому
понятию В, что WВ WА.
…
позвоночное
млекопитающее
Хищное млекопитающее
Кошка
Черная кошка
Черная трехлетняя кошка
…
ограничение
обобщение
21.
Обобщение (понятия А) –это переход к такому понятию В, что WA WB.
Ограничение (понятия А) –
это переход к непустому понятию В, что WВ WА.
…
реальная группа
добровольное объединение людей
спортивная команда
спортивная команда по олимп. виду спорта
спорт. команда по летнему олимп. виду спорта
футбольная команда
российская футбольная команда
российская ФК, играющая в Премьер-лиге
московская ФК, играющая в Премьер-лиге
ФК «Локомотив» (Москва)
обобщение
ограничение
…
22. I. ОБОБЩЕНИЕ И ОГРАНИЧЕНИЕ
Обобщение (понятия А) –это переход (от понятия А) к такому понятию В,
что WA WB.
Ограничение (понятия А) –
это переход (от понятия А) к такому непустому
понятию В, что WВ WА.
ВНИМАНИЕ !!!
Пределом обобщения служит универсальное понятие,
пределом ограничения – единичное. Собирательные
понятия обобщаются и ограничиваются только до
собирательных.
23. II. Булевы операции над объемами понятий.
1. ДополнениеЭто унарная операция порождения по данному
множеству А множества С, состоящего из тех и
только тех элементов универсума,
которые не принадлежат множеству А.
С = А
С: { x: х А }
Добрый человек недобрый человек
Летающее животное нелетающее животное
Собака не-собака
U
А
А
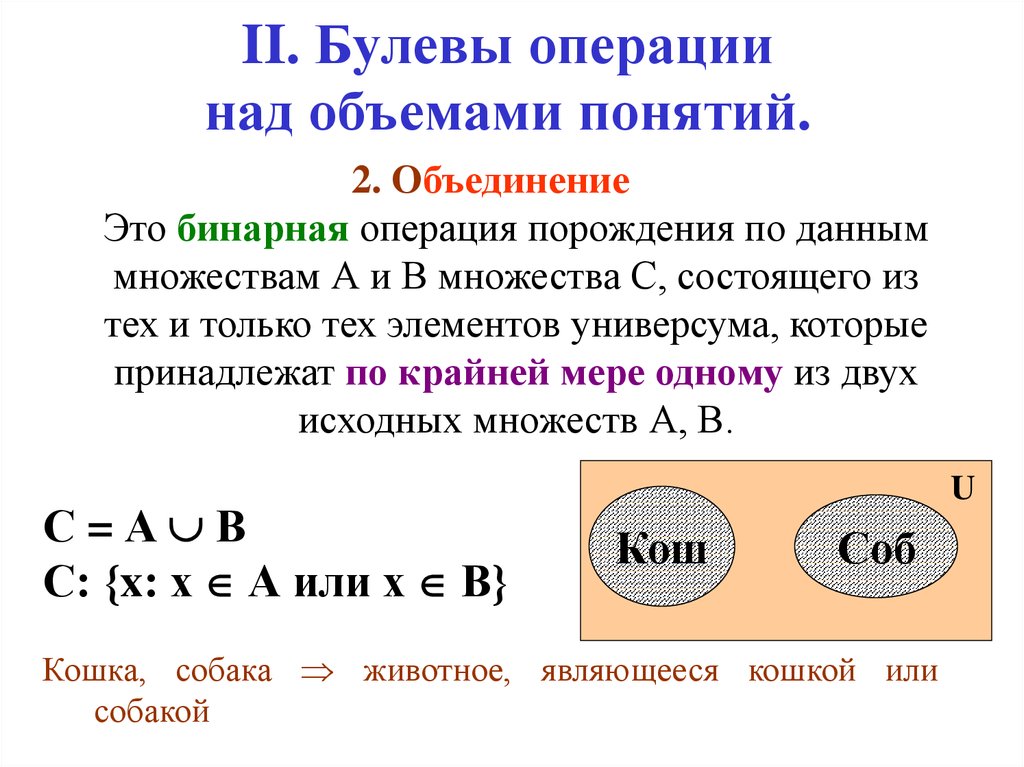
24. II. Булевы операции над объемами понятий.
2. ОбъединениеЭто бинарная операция порождения по данным
множествам А и В множества С, состоящего из
тех и только тех элементов универсума, которые
принадлежат по крайней мере одному из двух
исходных множеств А, В.
С=А В
С: {x: х А или х В}
U
Кош
Соб
Кошка, собака животное, являющееся кошкой или
собакой
25. II. Булевы операции над объемами понятий.
2. ОбъединениеЭто бинарная операция порождения по данным
множествам А и В множества С, состоящего из
тех и только тех элементов универсума, которые
принадлежат по крайней мере одному из двух
исходных множеств А, В.
С=А В
С: {x: х А или х В}
U
Муж
Шоф
Мужчина, шофер человек, являющийся мужчиной или
шофером
26. II. Булевы операции над объемами понятий.
2. ОбъединениеЭто бинарная операция порождения по данным
множествам А и В множества С, состоящего из
тех и только тех элементов универсума, которые
принадлежат по крайней мере одному из двух
исходных множеств А, В.
С=А В
С: {x: х А или х В}
ВМл
Кит
Кит, водное млекопитающее водное млекопитающее
U
27. II. Булевы операции над объемами понятий.
3. ПересечениеЭто бинарная операция порождения по данным
множествам А и В множества С, состоящего из
тех и только тех элементов универсума, которые
принадлежат одновременно двум исходным
множествам А, В.
С=А В
С: {x: х А и х В}
U
Кош
Соб
Кошка, собака (животное, являющееся кошкой и
собакой)
28. II. Булевы операции над объемами понятий.
3. ПересечениеЭто бинарная операция порождения по данным
множествам А и В множества С, состоящего из
тех и только тех элементов универсума, которые
принадлежат одновременно двум исходным
множествам А, В.
С=А В
С: {x: х А и х В}
U
М
М Ш
Ш
Мужчина, шофер человек, являющийся мужчиной и
шофером
29. II. Булевы операции над объемами понятий.
3. ПересечениеЭто бинарная операция порождения по данным
множествам А и В множества С, состоящего из
тех и только тех элементов универсума, которые
принадлежат одновременно двум исходным
множествам А, В.
С=А В
С: {x: х А и х В}
Кит, водное млекопитающее кит
ВМл
К
U
30. II. Булевы операции над объемами понятий.
4. Вычитание (из множества А множества В)Это бинарная операция порождения по данным
множествам А и В множества С, состоящего из
тех и только тех элементов универсума, которые
принадлежат множеству А и не принадлежат
множеству В. Очевидно, что данная операция
некоммутативна (А/В В/А)
С=А/В
С: {x: х А и х В}
U
К
С
Кошка, собака животное, являющееся кошкой и не
являющееся собакой (кошка)
31. II. Булевы операции над объемами понятий.
4. Вычитание (из множества А множества В)Это бинарная операция порождения по данным
множествам А и В множества С, состоящего из
тех и только тех элементов универсума, которые
принадлежат множеству А и не принадлежат
множеству В. Очевидно, что данная операция
некоммутативна (А/В В/А)
С=А/В
С: {x: х А и х В}
М
М/Ш
U
М Ш
Ш
Мужчина, шофер человек, являющийся мужчиной и не
являющийся шофером (белый цвет)
32. II. Булевы операции над объемами понятий.
4. Вычитание (из множества А множества В)Это бинарная операция порождения по данным
множествам А и В множества С, состоящего из
тех и только тех элементов универсума, которые
принадлежат множеству А и не принадлежат
множеству В. Очевидно, что данная операция
некоммутативна (А/В В/А)
С=А/В
С: {x: х А и х В}
Вмл
К
Кит, водное млекопитающее животное, являющееся
китом и не являющееся водным млекопитающим ( )
U
33. II. Булевы операции над объемами понятий.
4. Вычитание (из множества А множества В)Это бинарная операция порождения по данным
множествам А и В множества С, состоящего из
тех и только тех элементов универсума, которые
принадлежат множеству А и не принадлежат
множеству В. Очевидно, что данная операция
некоммутативна (А/В В/А)
С=А/В
С: {x: х А и х В}
ВМл
К
Водное млекопитающее, кит животное, являющееся
водным млекопитающим, но не китом
U
34. II. Булевы операции над объемами понятий.
4. Вычитание (из множества А множества В)Это бинарная операция порождения по данным
множествам А и В множества С, состоящего из
тех и только тех элементов универсума, которые
принадлежат множеству А и не принадлежат
множеству В. Очевидно, что данная операция
некоммутативна (А/В В/А)
С=А/В
С: {x: х А и х В}
U
БГ
Белый гриб, ножка белого гриба белый гриб
НБГ
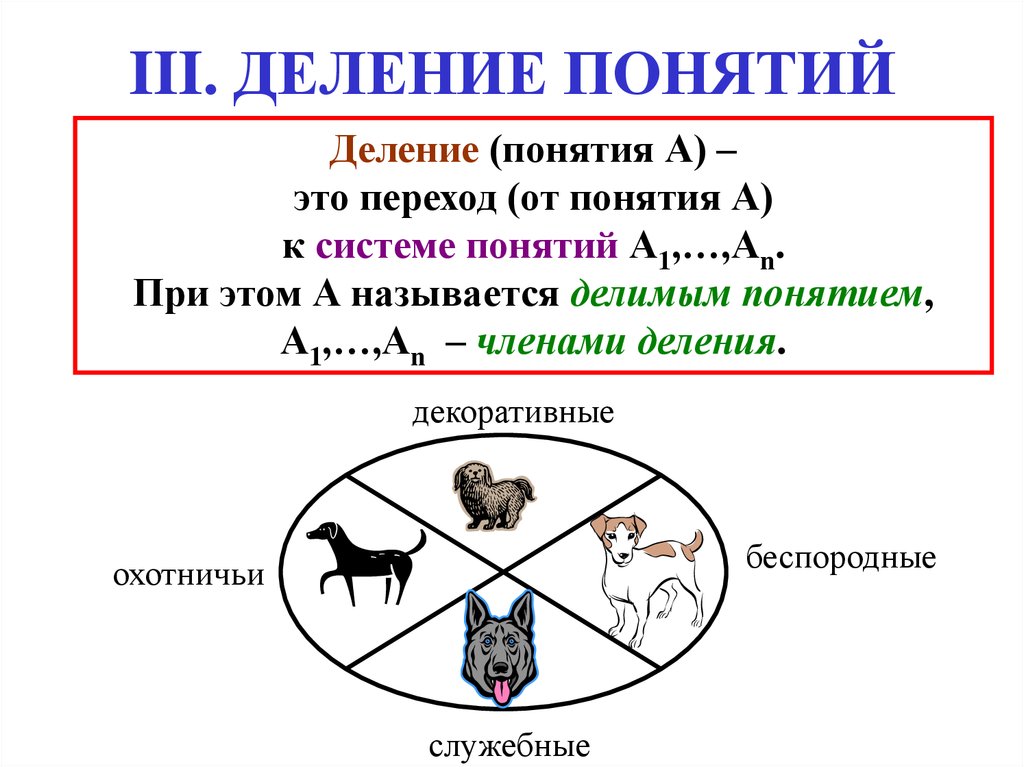
35. III. ДЕЛЕНИЕ ПОНЯТИЙ
Деление (понятия А) –это переход (от понятия А)
к системе понятий А1,…,Аn.
При этом А называется делимым понятием,
А1,…,Аn – членами деления.
декоративные
беспородные
охотничьи
служебные
36. III. ДЕЛЕНИЕ ПОНЯТИЙ
Деление (понятия А) –это переход (от понятия А) к системе понятий А1,…,Аn.
Деление называется квазиправильным,
если и только если выполняются следующие условия:
1. Каждое из понятий А1… Аn должно быть видовым для А: для
любого j WАj WA (логическое vs. мереологическое).
2. Каждое из видовых понятий А1… Аn должно быть непустым:
для любого j WАj .
3. Понятия из А1… Аn должны быть попарно несовместимы
(«Объемы членов деления не должны пересекаться»): для любых
i, j, где i j, WАi WAj .
4. Сумма объемов членов деления должна давать объем делимого
понятия: WА1 … WАn = WA (полнота деления).
37. III. ДЕЛЕНИЕ ПОНЯТИЙ
Деление (понятия А) –это переход (от понятия А) к системе понятий А1,…,Аn.
Деление называется квазиправильным,
если и только если выполняются следующие условия:
1.
2.
3.
4.
Требование «логического принципа»: WАj WA
Требование непустоты: WАj
Требование несовместимости: WАi WAj
Требование полноты: WА1 … WАn = WA
Деление называется правильным, если оно
квазиправильно, и осуществляется по одному основанию
(5-е требование).
5. Требование единства принципа деления
38. III. ДЕЛЕНИЕ ПОНЯТИЙ
Деление называется правильным, если оно удовлетворяетвсем пяти нижеследующим требованиям:
1.
2.
3.
4.
5.
Требование «логического принципа»: WАj WA
Требование непустоты: WАj
Требование несовместимости: WАi WAj
Требование полноты: WА1 … WАn = WA
Требование единства принципа деления
Основание деления –
это такая характеристика предметов
из объема делимого понятия, изменение которой
порождает систему членов деления.
39. III. ДЕЛЕНИЕ ПОНЯТИЙ
Основные типы деления1. Дихотомическое (деление надвое):
Предметы из А, обладающие свойством В
Предметы из А, не обладающие свойством В
Русские – Нерусские, Собаки – Не-собаки, Белые – Не-белые
и т.д.
2. По видоизменению основания
Рассматриваются все возможные модификации некоторой
содержательной (в смысле не исчерпываемой бинарной
оппозицией «есть – нет») характеристики (цвет глаз,
национальность и т.д.)
40. ОПРЕДЕЛЕНИЕ
Определение –это придание точного смысла
(содержания) языковому выражению.
В зависимости от роли и функций в
познавательном процессе выделяют
такие виды определений, как
номинальные и реальные.
41. ОПРЕДЕЛЕНИЕ
Реальное определение – это попытка придатьточный смысл/содержание (и, соответственно,
точно задать объем) термину (выражению),
который имеет, как правило, широкое
употребление и интуитивно очерченный объем.
Человек – это смеющееся животное
Номинальное определение - это введение нового термина
(выражения) или выбор (конвенционального характера) из
множества различных оттенков значения некоторого выражения
какого-то одного для каких-то конкретных целей.
Позитроном называется античастица по отношению к электрону.
Революцией будем называть социальный переворот, который…
42. ОПРЕДЕЛЕНИЕ
По своей структуре определения подразделяютсяна явные и неявные.
Явные определения имеют структуру
«А есть В»,
где А – определяемое выражение, В – определяющее.
Неявные определения такой структуры не имеют.
Например:
А есть то, что удовлетворяет условиям В1, В2,…, Вn.
43. ЯВНЫЕ ОПРЕДЕЛЕНИЯ
Как правило, это родо-видовые определения:А – это такое В, которое есть С.
Виды явных определений
1. Генетические: С есть указание на способ порождения
(образования) предметов А. («Окружность есть
замкнутая кривая линия, образованная вращением отрезка
вокруг одного из его концов»).
2. Операциональные: С есть указание на процедуру,
позволяющую распознать предметы А («Кислота –
жидкость, окрашивающая лакмус в красный цвет»).
3. Целевые (функциональные): С есть указание на функции
предметов А («Транспорт – средство, с помощью которого
осуществляется транспортировка людей и грузов») .
44. ЯВНЫЕ ОПРЕДЕЛЕНИЯ
Как правило, это родо-видовые определения:А – это такое В, которое есть С.
Виды явных определений
4. Атрибутивно-реляционные (квалифицирующие): С есть
описание особенностей самих предметов А, их свойств,
отношений («Полиглот – человек, знающий много
языков»; «Ромб – это равносторонний параллелограмм»).
5. Перечислительные (для общих терминов): С есть
перечисление всех объектов типа А («День недели – это
понедельник, вторник…воскресенье»).
45. НЕЯВНЫЕ ОПРЕДЕЛЕНИЯ
Процедура явных определений ведет либо к порочномукругу, либо в дурную бесконечность. Поэтому базовые
термины надо определять иначе. Например:
А есть то, что удовлетворяет условиям В1, В2,…, Вn.
Некоторые виды неявных определений
1. Индуктивные.
а) Х1,…, Хn есть А – базис индукции
б) Если Y есть А, то и Y* (Y’ и т.д.) есть А – индуктивный
переход
в) Ничто иное не есть А – ограничительный пункт
2. Аксиоматические
А есть то, что обладает свойствами, которые описываются
аксиомами В1, В2,…, Вn.
46. ТРЕБОВАНИЯ К ОПРЕДЕЛЕНИЯМ
Логические требования к определениям(зависят от вида и структуры)
Определение должно быть ясным: все термины,
входящие в определяющую часть уже должны иметь
четкий, определенный, прямой (а не метафорический)
смысл.
2. Определение должно быть соразмерным (для
реальных и явных): объемы определяемого и
определяющего терминов должны совпадать.
3. В определении не должно быть порочного круга
(для явных): определяемый термин не должен
встречаться в определяющей части.
1.
47. ОШИБКИ В ОПРЕДЕЛЕНИЯХ
Эго-транцендированием называется экзистенциальнаявнутренняя деструкция имманентных границ единства
апперцепции экстатического характера, сопровождаемая
элиминацией демаркационных полюсов рациональной
субъективности.
Коммунизм – это молодость мира.
Собака – это домашнее животное.
Смерть – это естественный конец всякого живого существа.
Бочка – это деревянный сосуд для хранения сыпучих тел.
Кит – это крупнейшая на Земле рыба, выкармливающая
детенышей молоком.
Светлая комната – комната, в которой светло.
Математика – это то, чем занимаются математики (??? –
круг ли?)



































 Математика
Математика








