Похожие презентации:
Алгебра матриц. Комплексные числа
1. Алгебра
Лекции – 36часовПр. зан. – 36 часов
Зачет
Лектор: доц. Жмурова Ирина Юньевна
Ассистент: ст. пр. Игнатова Анна Васильевна
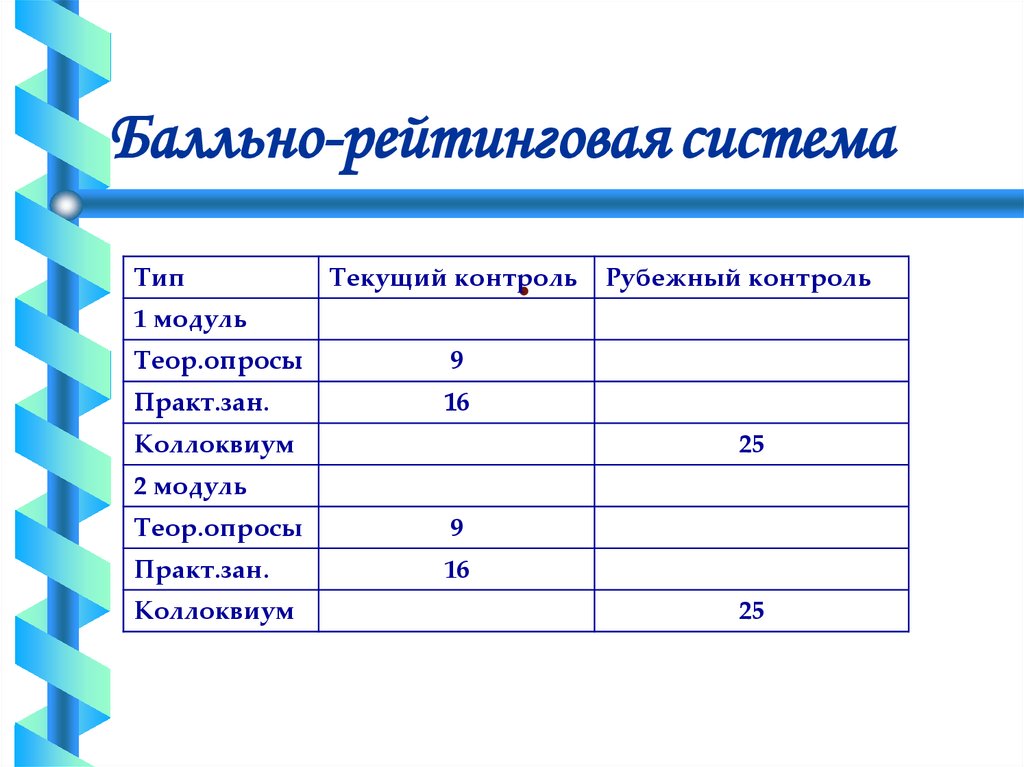
2. Балльно-рейтинговая система
Тип.
Текущий контроль
Рубежный контроль
1 модуль
Теор.опросы
9
Практ.зан.
16
Коллоквиум
25
2 модуль
Теор.опросы
9
Практ.зан.
16
Коллоквиум
25
3. Требования
Опросына лекциях: 0; 0,25; 0,5; 1
Отсутствие на лекции: – 1
Итого (max): 18
Коллоквиум (max): 2 25 =50
Практические занятия: 32
Бонусные баллы (max): 10
4. Литература (учебники)
А.Г.Курош.Курс высшей алгебры
Варпаховский
Ф.Л., Солодовников А.С.
Алгебра. Ч. 1.
Кострикин А.И. Введение в алгебру
Б. Ван дер Варден. Алгебра
5. Литература (задачники)
ПроскуряковИ.В. Сборник задач по
линейной алгебре
Варпаховский
Ф.Л., Солодовников А.С.
Задачник-практикум по алгебре и
теории чисел
6.
Модуль1. Алгебра матриц
Модуль 2. Комплексные числа
7. Модуль 1. Алгебра матриц
8. Системы линейных алгебраических уравнений
Def1. Система линейных алгебраических
уравнений (СЛАУ):
a11 x1 a12 x2 a1n xn b1
a x a x a x b
21 1 22 2
2n n
2
(1)
am1 x1 am 2 x2 amn xn bm
9. Системы линейных алгебраических уравнений
Def 2. Набор чисел ω1,ω2,…,ωп называетсярешением системы (1), если при подстановке
чисел ωi в каждое уравнение системы (1)
получается система верных равенств.
Def 3. Две СЛАУ называются
эквивалентными, если они имеют одинаковые
решения, либо не имеют решений
10. Системы линейны алгебраических уравнений
4. Матрицей системы (1) называетсяматрица следующего вида:
Def
а11
а21
А
а т1
а12
а22
ат 2
а1п
а2 п
атп
11. Системы линейны алгебраических уравнений
5. Расширенной матрицей системы(1) называется матрица следующего вида:
Def
а11 а12
а21 а22
А
а
т1 ат 2
а1п b1
а2 п b2
атп bm
12. Метод Гаусса
Элементарными преобразованиямиСЛАУ называются следующие:
1. Перемена местами двух уравнений
2. Умножение уравнения на число,
отличное от нуля
3. Прибавление к одному уравнению
другого, умноженного на число
Def.
13. Метод Гаусса
Теорема1. Если одна СЛАУ получена из
другой с помощью конечного числа
элементарных преобразований, то она
эквивалентна данной.
14. Метод Гаусса
Теорема2. Любую СЛАУ с помощью
конечного
числа
элементарных
преобразований можно привести к
ступенчатому виду.
NB Этот алгоритм называют алгоритмом
Гаусса
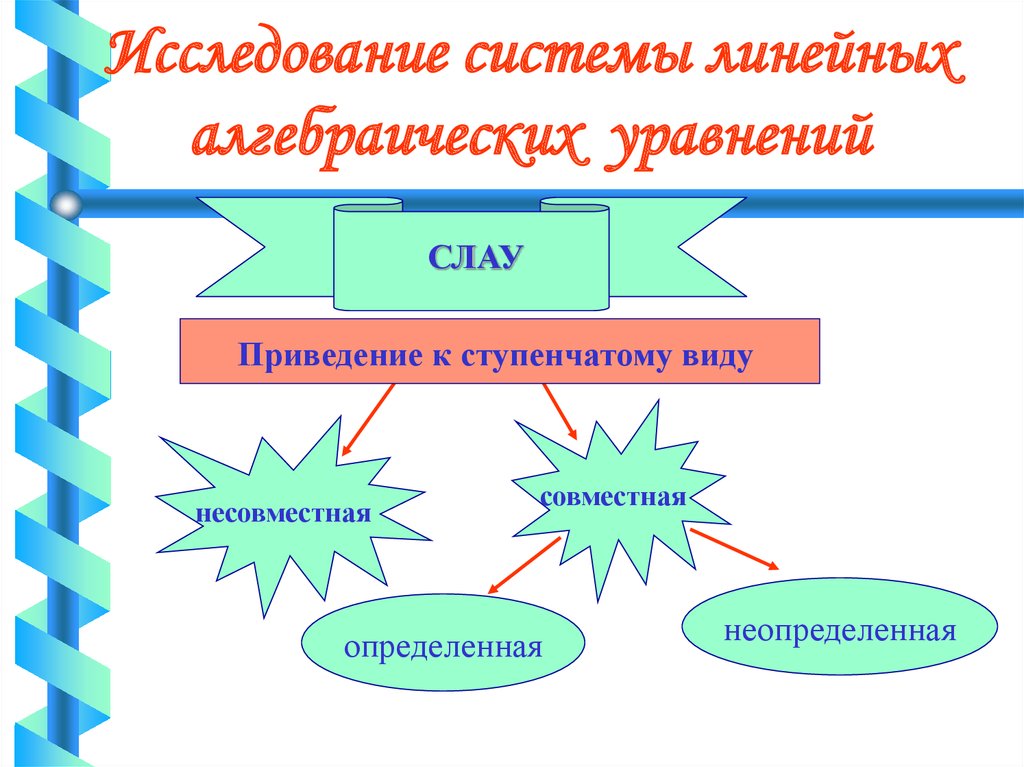
15. Исследование системы линейных алгебраических уравнений
СЛАУПриведение к ступенчатому виду
несовместная
совместная
определенная
неопределенная
16. Критерий совместности системы
Теорема3. Для того, чтобы СЛАУ была
совместна, необходимо и достаточно,
чтобы
после
приведения
ее
к
ступенчатому виду в ней отсутствовали
бы уравнения вида 0=b, где b 0
17. Решение неопределенной СЛАУ
Привести систему (1) к ступенчатомувиду.
2.
Выделить свободные и главные
неизвестные.
3. Свободные неизвестные перенести в
правую часть с противоположным
знаком.
1.
18. Решение неопределенной СЛАУ
4. В левой части провести обратный ход методаГаусса.
5. Записать общее решение системы.
6. При необходимости найти частные решения
системы
NB 1. Если система неопределенная, то она
имеет бесконечное множество решений.
NB 2. Однородная система всегда совместна.
19. Примеры решения систем
х1 х2 х3 33 х1 х2 4 х3 6
2 х 8 х х 7
1
2
3
3 х1 5 х2 2 х3 4 х4 2
7 х1 4 х2 х3 3 х4 5
5 х 7 х 4 х 6 х 3
2
3
4
1
20. Примеры решения систем
2 х1 х2 х3 2 х4 3 х5 26 х 3 х 2 х 4 х 5 х 3
2
3
4
5
1
6 х1 3 х2 4 х3 8 х4 13 х5 9
4 х 2 х х х 2 х 1
2
3
4
5
1
4 х1 2 х2 2 х3 4 х4 6 х5 4
21. Операции над матрицами
M m n ( R) { A матрица т п}b11 b12 b1п
а11 а12 а1п
А В
а
b
b
b
тп
т1 т 2
т1 ат 2 атп
A aij
т n
i 1 j 1
B bij
A, B M m n ( R)
т n
i 1 j 1
22. Условие равенства матриц
Две матрицы из Mmxn(R) называютсяравными, если все элементы, стоящие на
одних и тех же местах равны
Def.
23. Сложение матриц
1. Суммой матриц А и В из Mmxn(R)называются матрица, элементы которой
равны сумме соответствующих элементов
матриц А и В
Def
24. Свойства операции сложения
10. Коммутативность20. Ассоциативность
30. Наличие нейтрального элемента
40. Наличие нейтрализующего элемента
NB 1. Матрица –А называется матрицей,
противоположной к А, или противоположной
матрицей.
NB 2. Алгебраическая структура, обладающая
свойствами 10 – 40, называется абелевой
(коммутативной) группой.
25. Умножение матрицы на число
def.Пусть
А Мm n(R),
λ R.
Произведением матрицы А и числа λ
называется матрица, каждый элемент
которой
получается
произведением
элемента матрицы А и числа λ
26. Свойства операции умножения матрицы на число
10.1·А=А
20. λ(μА)=(λμ)А
30. λ(А+В)=λА+λВ
40. (λ+μ)А=λА+μА
50. (λА)В=λ(АВ)=А(λВ)
27. Умножение матриц
R арифметические векторып
а а1 , а2 , , ап , ai R
b b1 , b2 , , bп , bi R
(a, b) скалярное произведение векторов
n
(a , b) a1b1 a 2b2 a n bn ai bi
i 1
28. Свойства скалярного произведения арифметических векторов
Коммутативность20. Однородность
30. Аддитивность
40. Неотрицательность
10.
29. Определение произведения квадратных матриц
A, B M 2 2 ( R) M 2 ( R)А
АВ
x
z
x
В
z
y
t
y
t
x z y t
x z y t
30. Определение произведения матриц
A, B M 2 2 ( R) M 2 ( R)x
y
2
В B
z
t
А1 ( , )
А2 ( , )
1
А1 , В
АВ
1
А2 , В
1
А , В
А , В
2
1
2
2
31. Определение произведения матриц
A aijB bij
n n
i 1 j 1
A1 , B
1
A2 , B
AB
A , B1
п
1
n n
i 1 j 1
A , B
A , B
2
A , B
A , B
2
1
2
A , B
2
п
п
1
п
2
п
Aп , B
32. Определение произведения матриц
1 1 43 2 3
A 2
7 9 B 4 1
1
2 0 4
0 1
2
33. Свойства операции умножения квадратных матриц
Коммутативность20. Ассоциативность
30. Существование нейтрального элемента
40. Существование обратного элемента
10.
34. Умножение прямоугольных матриц
Условиесогласования
Число столбцов левой матрицы должно
быть равно числу строк правой
35. Умножение прямоугольных матриц
def. Пусть А Мm n(R), B Mn r(R).Произведением матриц А и В называется
матрица С Мm r(R), вычисляемая по
правилу:
36. Умножение прямоугольных матриц
A aijB bij
т n
i 1 j 1
A1 , B
1
A2 , B
AB
A , B1
т
1
n r
i 1 j 1
A , B
A , B
2
A , B
A , B
2
1
2
A , B
2
т
r
1
r
2
r
Aт , B
37. Свойства операции умножения матриц (в общем виде)
Коммутативность20. Ассоциативность
30. Существование нейтральных
элементов: левого и правого
40. Дистрибутивность относительно
сложения
10.
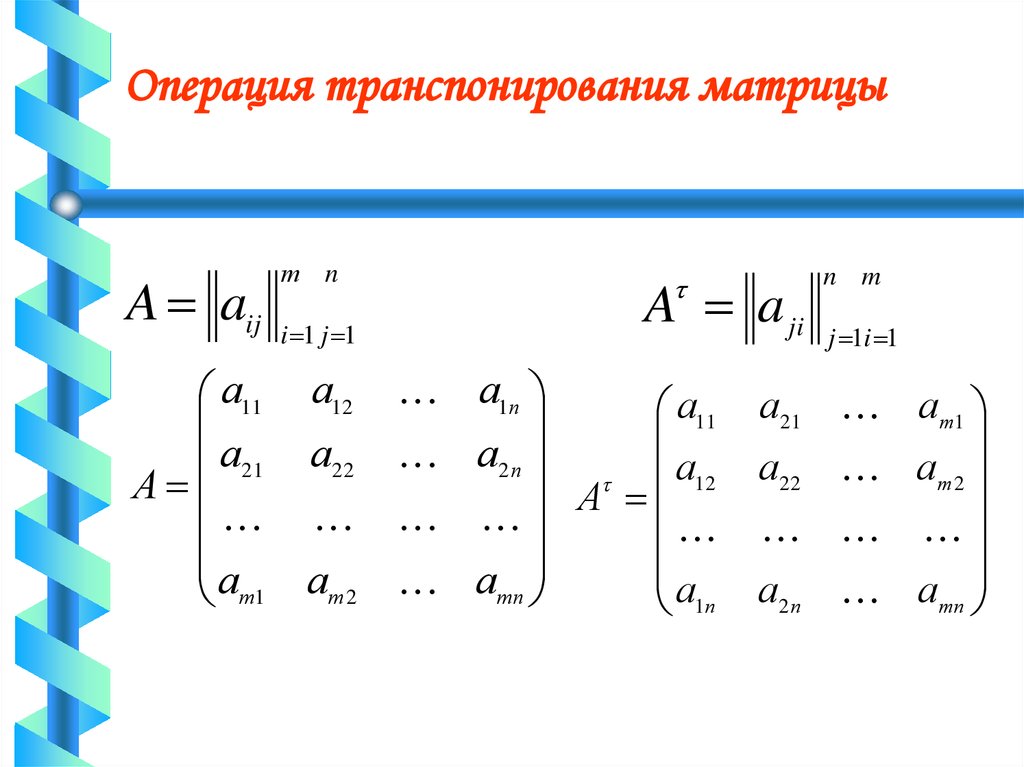
38. Операция транспонирования матрицы
A aijа11
а21
А
ат1
т n
i 1 j 1
A a ji
а1п
а11 а21
а22 а2 п
а12 а22
А
ат 2 атп
а1п а2 п
а12
n m
j 1i 1
ат1
ат 2
атп
39. Свойства операции транспонирования
10. (А+В)τ=Аτ + Вτ20. (λА)τ =λАτ
30. (Аτ)τ =А
40. (АВ)τ=ВτАτ
40.
Определитель квадратной матрицыОпределителем квадратной матрицы А Мп(R)
называют ее числовую характеристику,
a11
det A A
a12 a1n
a21 a22 a2 n
an1 an 2 ann
41.
Определитель квадратной матрицыОпределитель квадратной матрицы А Мп(R) – ее
числовая характеристика
a11
det A A
a12 a1n
a21 a22 a2 n
an1 an 2 ann
42.
Определитель квадратной матрицыОпределитель матрицы второго порядка:
а11
а12
а21 а22
а11а22 а12а21
43. Определитель 3-го порядка
а11а12
а13
а21 а22
а23
а31 а32
а33
а11а22а33 а13а21а32 а12а23а31
а13а22а31 а12а21а33 а11а23а32
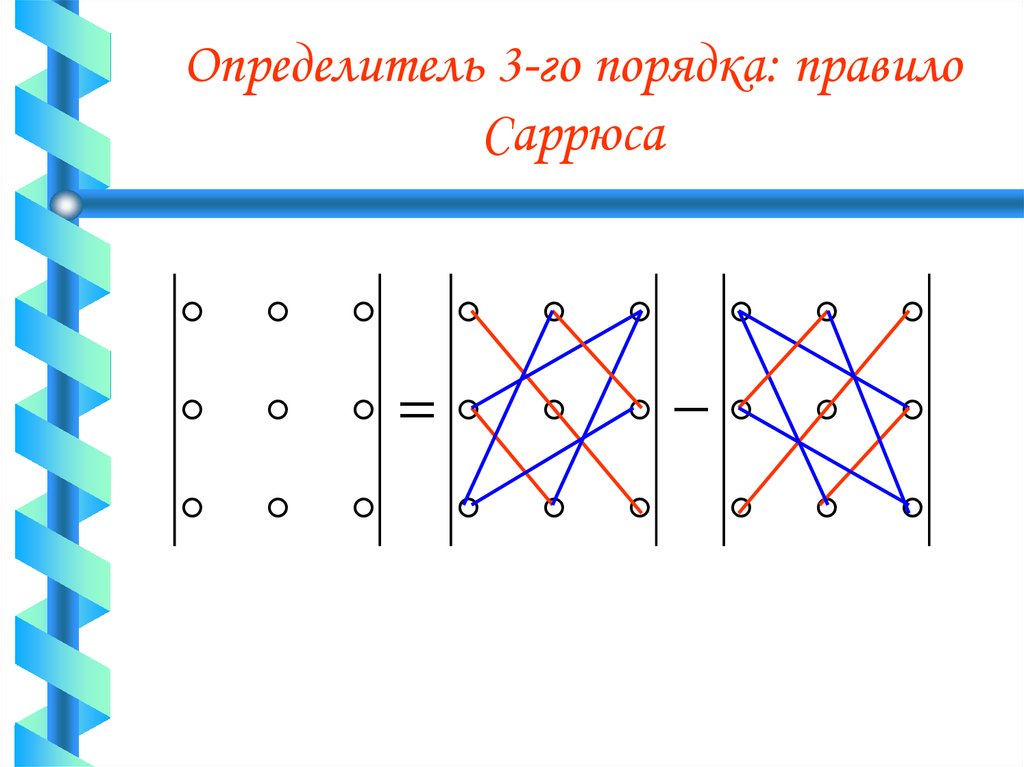
44. Определитель 3-го порядка: правило Саррюса
45. Определитель n-го порядка
а11 а1nаn1 аnn
n
sgn a
i
S n
i
i 1
sgn а а а
S n
1 1
2
2
n
n
46. Свойства определителей
Определитель п-го порядкасодержит п! слагаемых, из которых
половина берется со знаком «+», а
половина – со знаком «–»
10
47. Свойства определителей
При транспонированииопределитель матрицы не меняется
NB Из свойства 20 следует, что все
свойства определителей можно
формулировать как для строк, так и
для столбцов
20
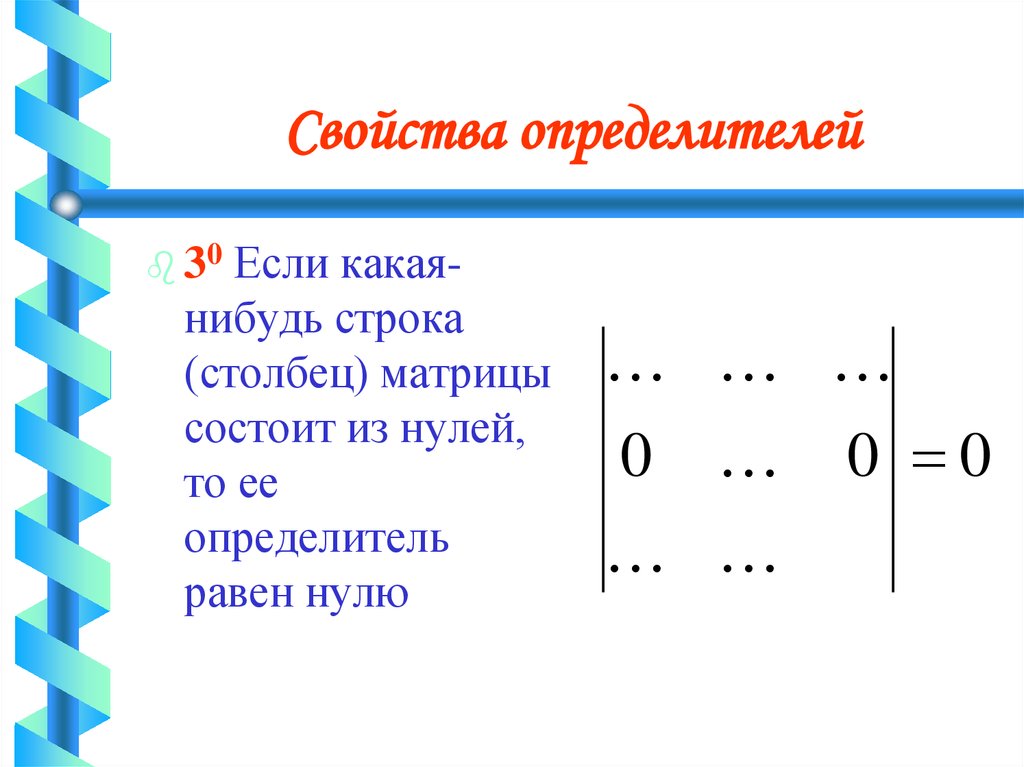
48. Свойства определителей
Если какаянибудь строка(столбец) матрицы
состоит из нулей,
то ее
определитель
равен нулю
30
0
0 0
49. Свойства определителей
40 Если матрица В получена из матрицы А элементарным преобразованием 1 типа, то det B = – det A.ai 1
ai 2
ain
a j1 a j 2
a jn
ai 1
ain
aj1
aj 2
a jn
ai 2
50. Свойства определителей
50 Если матрица В получена из матрицы Аэлементарным преобразованием 2 типа, то
det B = λ det A.
ai1 aiт ai1 aiт
51. Свойства определителей
60 Если строки (столбцы) матрицыпропорциональны, то ее определитель равен
нулю.
ai1
ai 2
ain
0
kai1 kai 2 kain
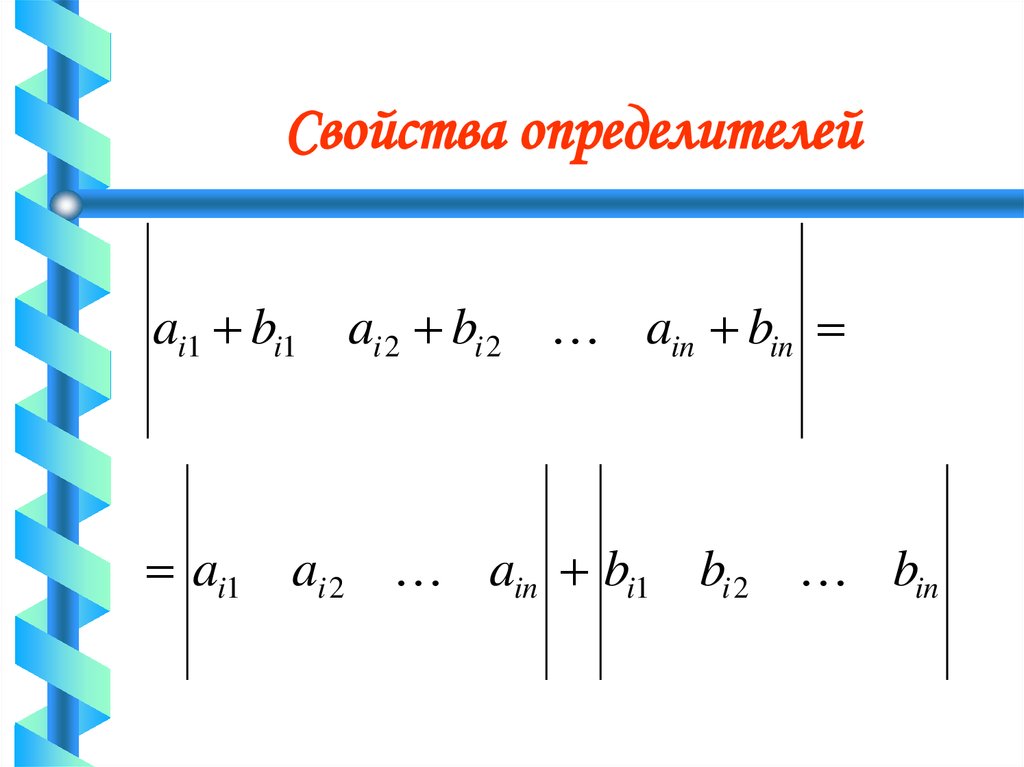
52. Свойства определителей
70 Если какая-нибудь строка (столбец)матрицы есть сумма двух
арифметических векторов, то ее
определитель равен сумме
определителей, которые получаются из
исходной матрицы заменой на
соответствующие строки.
53. Свойства определителей
ai1 bi1 ai 2 bi 2 ain binai1 ai 2 ain bi1 bi 2 bin
54. Свойства определителей
Если матрица В получена изматрицы А элементарным
преобразованием 3 типа, то ее
определитель не изменится:
det B = det A.
80
55. Свойства определителей
ai1ain
a j1 ai1 a jn ain
ai1 ain
a j1 a jn
56. Разложение определителя по элементам строки или столбца
Def. МиноромMij, дополнительным к
элементу aij называется определитель
п-1-го порядка, полученный из
определителя матрицы вычеркиванием
строки и столбца, содержащего
элемент aij
57. Разложение определителя по элементам строки или столбца
M ija11
a1 j 1
a1 j 1
a1n
ai 11 ai 1 j 1
ai 1 j 1 ai 1 n
ai 11 ai 1 j 1
ai 1 j 1 ai 1 n
an1
an j 1
an j 1
ann
58. Разложение определителя по элементам строки или столбца
Def. Алгебраическим дополнением элементаaij называется его дополнительный минор,
взятый с определенным знаком:
Aij=(–1)i+jMij
Ех.
1
2
1
А 3
5
7
3 4 2
59. Малая теорема Лапласа
Определитель п-го порядка равен суммепроизведений элементов какой-нибудь строки
(столбца) и их алгебраических дополнений.
n
det A aij Aij
j 1
n
det A aij Aij
i 1
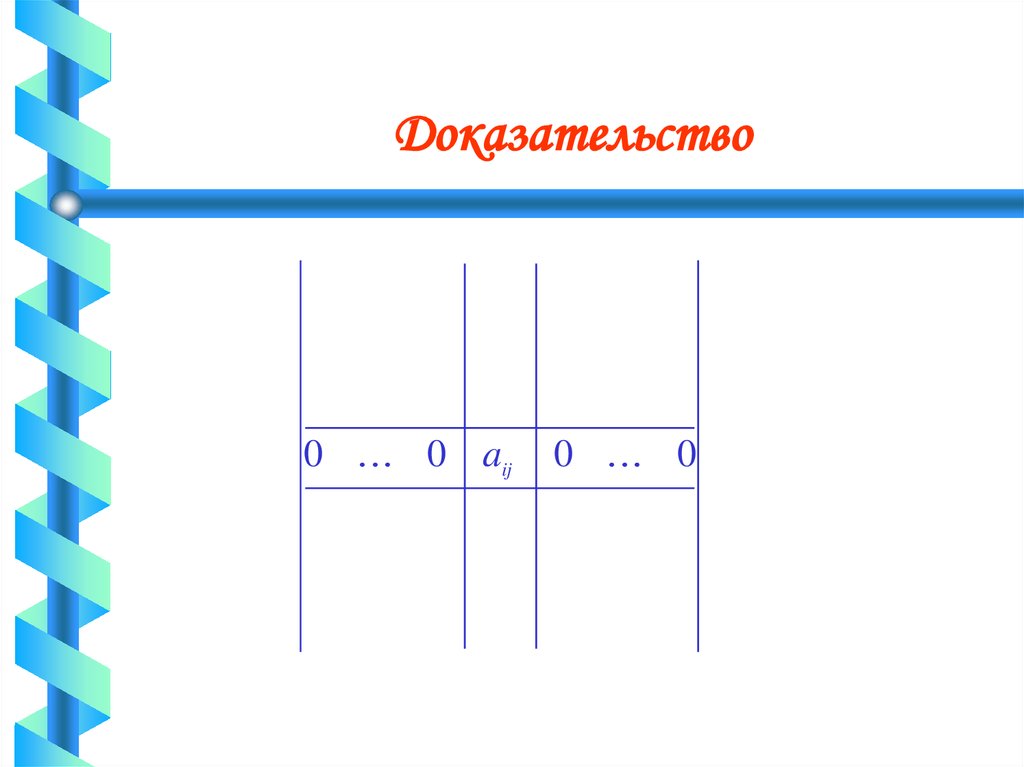
60. Доказательство
a11a21
an 1,1
0
a12
a22
an 1, 2
0
a1, n 1
a2 , n 1
an 1, n 1
0
a1n
a2 n
an 1, n
ann
61. Доказательство
0 0 aij0 0
62. Доказательство
аi 1ai 2 ain
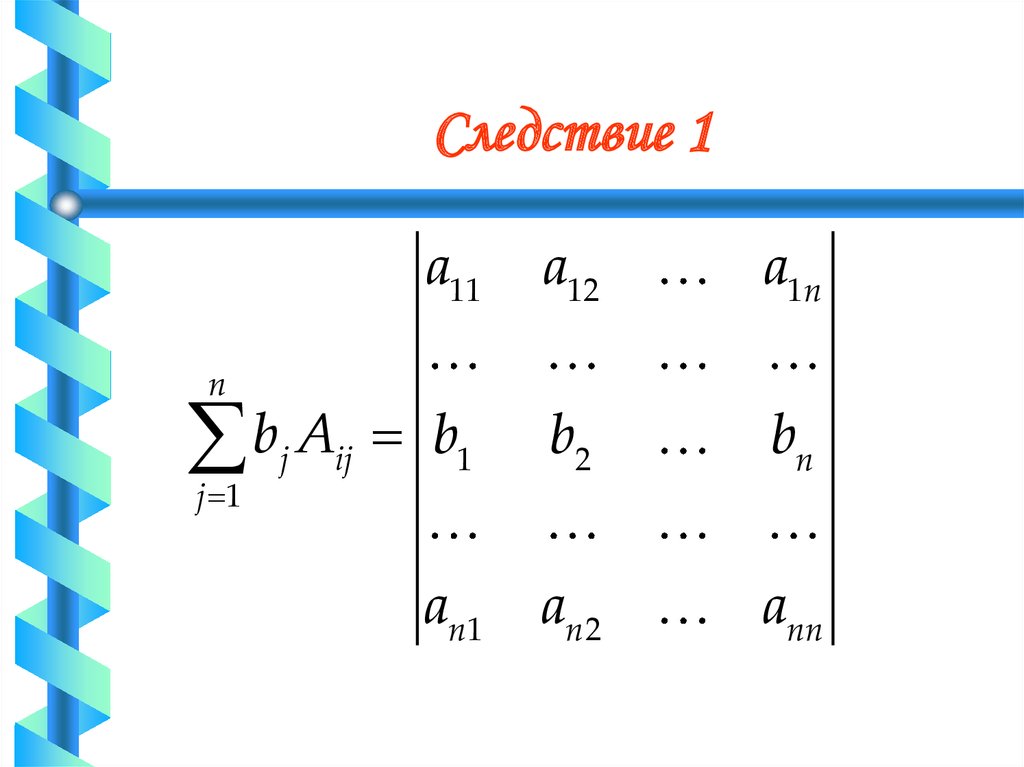
63. Следствие 1
Пусть b1,b2,…,bn – произвольные числа.Сумма
n
b A
j
ij
j 1
равна определителю матрицы В, которая
получена из матрицы А заменой i-й строки
числами b1,b2,…,bn
64. Следствие 1
nb A
j 1
j
ij
a11
a12
a1n
b1
b2
bn
an1
an 2
ann
65. Следствие 2
Сумма произведений элементов какой-нибудьстроки (столбца) и алгебраических элементов
другой строки (столбца) равна нулю
n
a
j 1
kj
Aij 0, k i
66. Следствие 3
k i0,
j 1 akj Aij det A, k i
n
67. Обратная матрица
А Мп(R)def. Матрица А–1 Мп(R) называется
обратной к матрице А, если
А А А А Е
1
1
def. Матрица, имеющая обратную, называется
обратимой
68. Свойства обратной матрицы
(А–1 )–1 =А20 Произведение обратимых матриц
обратимо, причем (АВ)–1 = В–1А–1
30 Если матрица А обратима, то
уравнения (1) АХ=В и (2) ХА=В имеют
решение
1
0
–1
–1
4 det A = (det A) =
10
det A
69. Свойства обратной матрицы
Теорема(критерий обратимости
матрицы) Для того, чтобы матрица А
была обратима, необходимо и
достаточно, чтобы ее определитель был
отличен от нуля
def Если определитель матрицы
отличен от нуля, матрицу называют
невырожденной
70. 2 способа нахождения обратной матрицы
1 ˆ1 способ : А
A
det A
2 способ : метод Гаусса
1
А Е ~ E A
1
1 1 1
А 2 1 1
1 2 1
71. Теорема Крамера
Пусть(1)
–
система
линейных
алгебраических уравнений с квадратной
матрицей
a11 x1 a12 x2 a1n xn b1
a x a x a x b
21 1 22 2
2n n
2
(1)
aп1 x1 aп 2 x2 aпn xn bп
72. Теорема Крамера
Если определитель матрицы системы (1)отличен от нуля, то система (1) является
определенной, а ее единственное решение
определяется формулами
det Ai
xi
det A
где Аi – матрица, полученная из матрицы А
заменой i-го стоблца столбцом свободных
членов
73. Пример решения системы по правилу Крамера
x1 x2 x3 33 x1 x2 4 x3 6
2 x 8 x x 7
1
2
3
74. Модуль 2. Комплексные числа
2i
+ 1= 0
75. 1. Историческая справка
Впервые мнимые величины появились вработе Дж. Кардано «Великое искусство,
или об алгебраических правилах» в 1545
году.
Пользу мнимых чисел при решении
кубических уравнений впервые оценил
итальянский ученый Р. Бомбелли (1572).
Символ i предложил российский ученый Л.
Эйлер (1777, опубликовано1794).
Задача о выражении степени n из комплексного
числа была в основном решена в работах
английских ученых А. Муавра (1707, 1724) и Р.
Котеса (1722).
76. 1. Историческая справка
Термин«комплексное
число»
ввел
французский ученый Л. Карно (1803).
В употребление термин вошел после работ
К. Гаусса (1831).
Полное
геометрическое
истолкование
комплексных чисел и действий над ними
появилось впервые в работе датского ученого
К. Весселя (1799).
Геометрическое
представление
комплексных
чисел
называют
иногда
«диаграммой Аргана» в честь швейцарского
ученого Ж. Аргана.
77. Абрахам Муавр (Moivre) (1667 – 1754)
2. Требования, предъявляемые ксистеме комплексных чисел
1. <C, +, > – поле
2. Уравнение x2 + 1 = 0 имеет решение в
поле С
3. Множество действительных чисел –
подмножество множества комплексных
чисел и все операции согласованы.
78. Карл Фридрих Гаусс (Gauss) (1777 – 1855)
Построение множества комплексныхчисел
C = R2={(a,b): a,b R}
Условие равенства:
(a,b)=(a1,b1) a=a1, b=b1
Операция сложения:
(a,b)+(a1,b1)=(a +a1,b +b1)
Операция умножения:
(a,b) (a1,b1)=(aa1 –bb1, ab1+ba1)
79. Леонард Эйлер (Eular) (1707 – 17830)
Классическая (алгебраическая) формакомплексного числа
z=(a,b)=(a,0)+(0,b)=(a,0)+(b,0)(0,1) ,
(a,0) →a, (b,0)→ b, (0,1)→i, i2= – 1.
z=a+bi, a,b – действительные числа,
i – мнимая единица, определяемая равенством
i2= – 1.
a=Re z - действительная часть комплексного
числа z.
b=Im z - мнимая часть комплексного числа z.
(иногда мнимой частью называют bi)
80. 2. Требования, предъявляемые к системе комплексных чисел
Равные комплексные числаz1=a+bi, z2=c+di
z1=z2, если a=c, b=d.
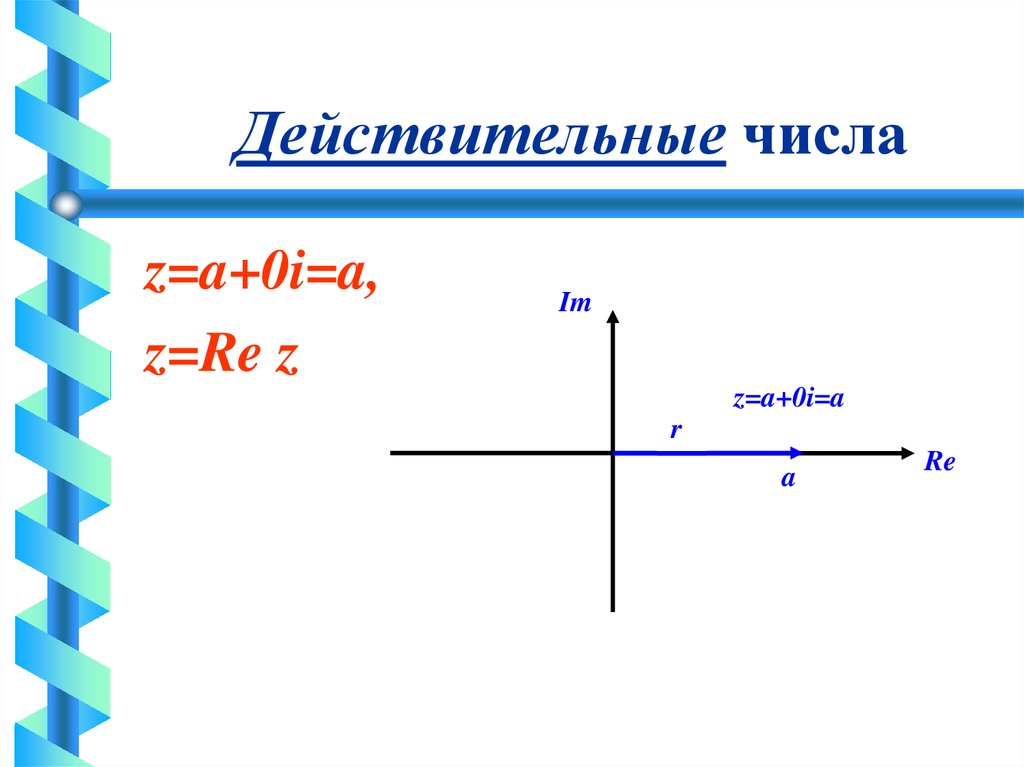
81. Построение множества комплексных чисел
Действительные числаz=a+0i=a,
z=Re z
Im
z=a+0i=a
r
a
Re
82. Классическая (алгебраическая) форма комплексного числа
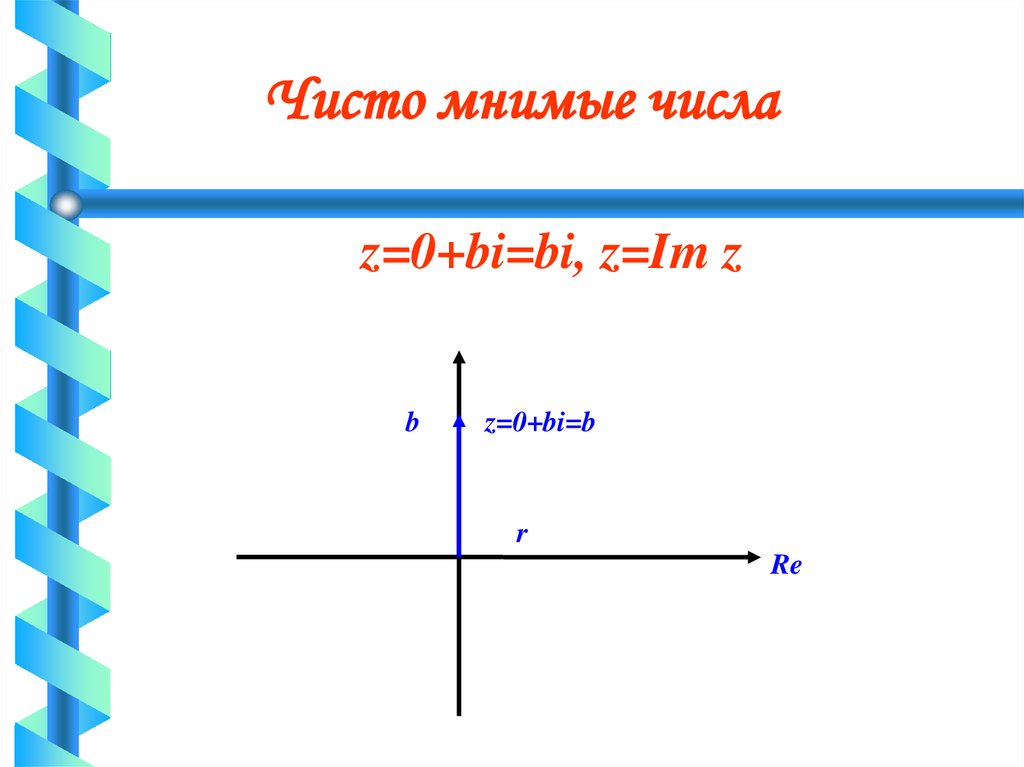
Чисто мнимые числаz=0+bi=bi, z=Im z
b
z=0+bi=b
r
Re
83. Равные комплексные числа
Действия над комплексными числамив алгебраической форме
Сложение: (a+bi) + (c+di) = (a+c) + (b+d)i
Вычитание: (a+bi) – (c+di) = (a – c) + (b – d)i
Умножение: (a+bi) (c+di) = (ac – bd) + (ad+bc)i
Деление:
a bi ( ac bd ) (bc ad )i
2
2
c di
c d
84. Действительные числа
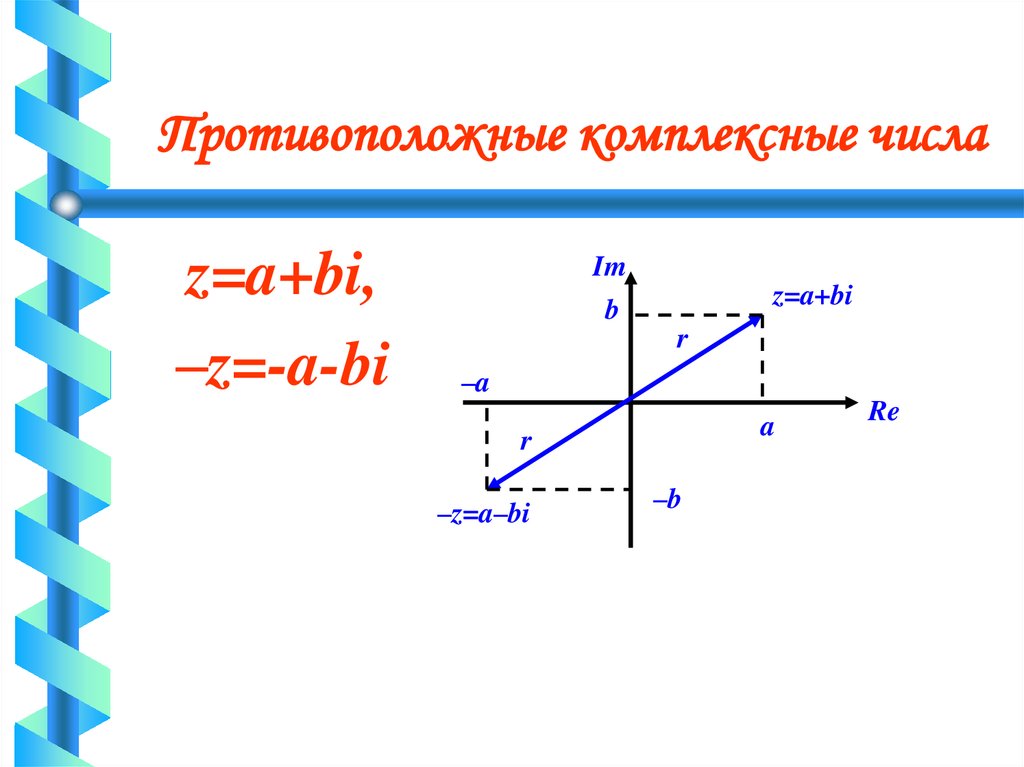
Противоположные комплексные числаz=a+bi,
–z=-a-bi
Im
z=a+bi
b
r
–a
a
r
–z=a–bi
–b
Re
85. Чисто мнимые числа
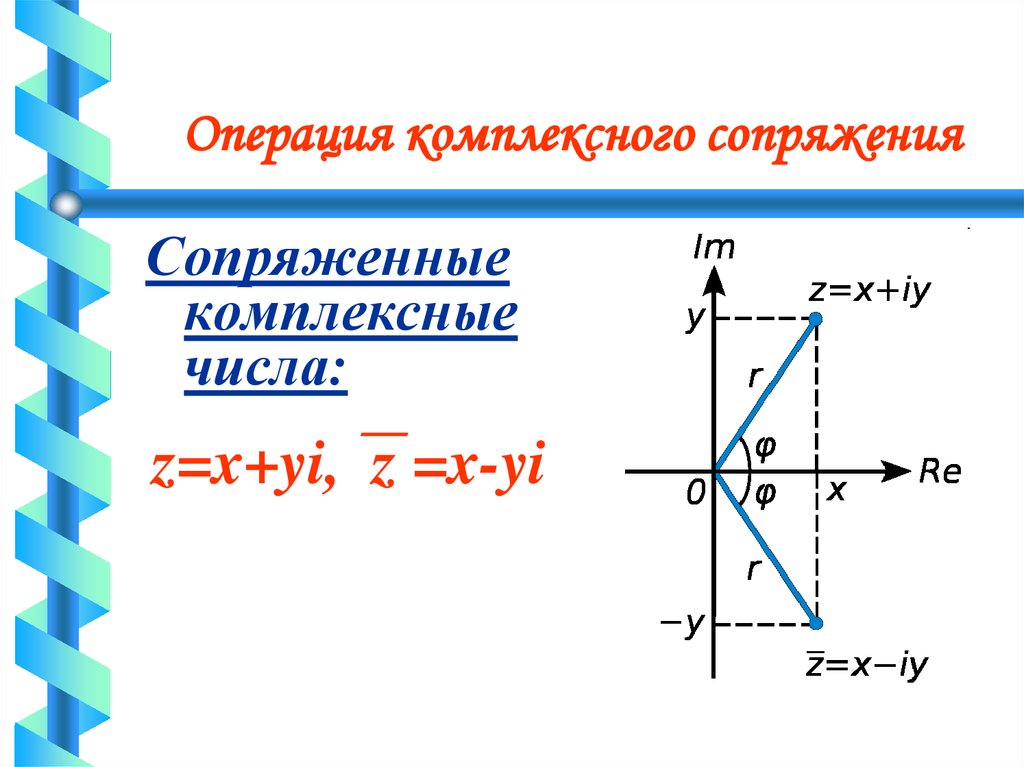
Операция комплексного сопряженияСопряженные
комплексные
числа:
z=x+yi, z =x-yi
86. Действия над комплексными числами в алгебраической форме
Свойства операции комплексногосопряжения
1 . z1 z 2 z1 z 2
5 . z z z R
2 . z1 z2 z1 z2
6 . z z 2 Re z
0
0
0
3.
z1 z1
z2 z2
4. z z
0
0
0
7 . z z 2 Im z
0
8 . zz z
0
2
87. Противоположные комплексные числа
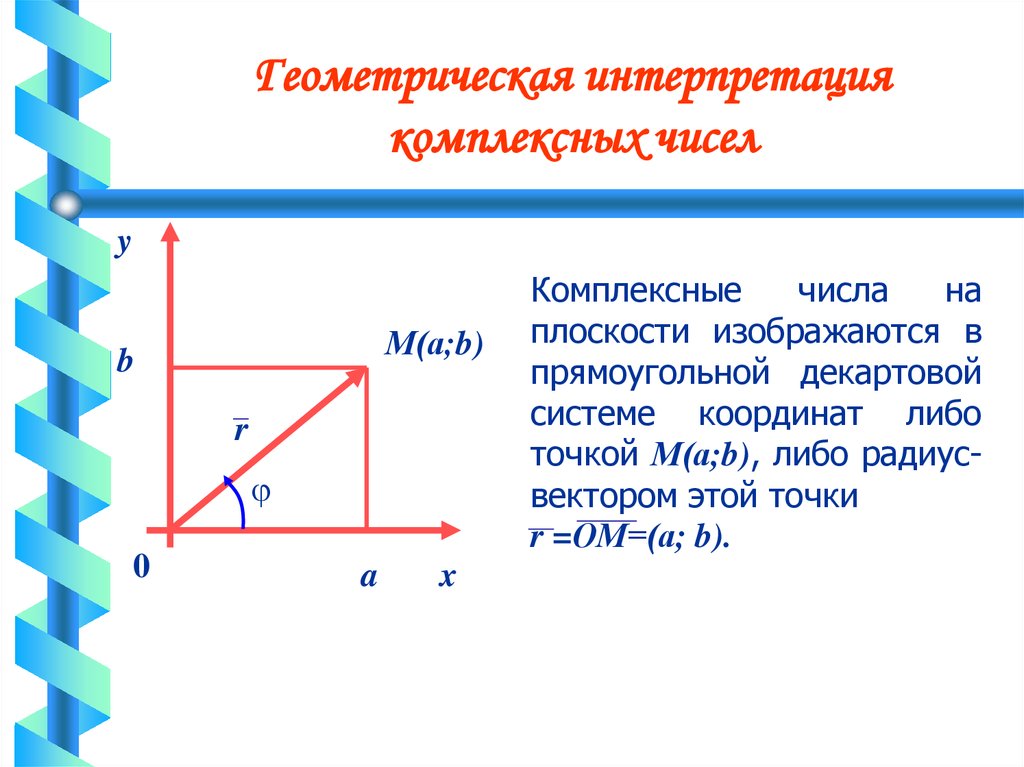
Геометрическая интерпретациякомплексных чисел
y
М(а;b)
b
r
0
a
x
Комплексные
числа
на
плоскости изображаются в
прямоугольной декартовой
системе координат либо
точкой М(а;b), либо радиусвектором этой точки
r =ОМ=(а; b).
88. Операция комплексного сопряжения
3. Геометрическая интерпретациякомплексных чисел
89. Свойства операции комплексного сопряжения
4. Модуль и аргумент комплексного числаМодуль комплексного
числа
z r a b
2
2
Аргумент
комплексного числа
arg z = ,
Sin = b/r,
Cos φ = a/r
0≤ < 2 .
90. Геометрическая интерпретация комплексных чисел
5. Алгоритм перехода от алгебраической формыкомплексного числа к тригонометрической
1. Найти модуль
комплексного числа
z= a + bi
2. Найти аргумент φ
комплексного числа из
условий:
3. Записать комплексное
число в
тригонометрической
форме:
z r a b
2
2
a
b
cos , sin
r
r
z a bi r (cos i sin )
91. 3. Геометрическая интерпретация комплексных чисел
6. Алгоритм перехода от тригонометрическойформы комплексного числа к алгебраической
z r (cos i sin )
r cos i r sin
a
b
a bi
92. 4. Модуль и аргумент комплексного числа
7. Пример перехода от алгебраической формыкомплексного числа к тригонометрической
Z = 2 +2i,
a = 2, b = 2,
r 2 2 2 2 8 2 2.
y
2
2
cos
,
2 2
2
2
2
sin
2 2
2 4,
2
z 2 2 (cos i sin ).
4
4
0
r
φ
2
x
93. 5. Алгоритм перехода от алгебраической формы комплексного числа к тригонометрической
7. Пример перехода от тригонометрическойформы комплексного числа к алгебраической
5
5
z 4 cos
i sin
3
3
5 1
cos
3 2
5
3
sin
3
2
1
3
z 4 i
2 2i 3
2
2
94. 6. Алгоритм перехода от тригонометрической формы комплексного числа к алгебраической
8. Действия с комплексными числами втригонометрической форме
z1 r1 (cos 1 i sin 1 ), z 2 r2 (cos 2 i sin 2 )
z1 z 2 r1 r2 cos 1 2 i sin 1 2
z1 r1
cos 1 2 i sin 1 2
z 2 r2
z r cos n i sin n формула Муавра
n
n
95. 7. Пример перехода от алгебраической формы комплексного числа к тригонометрической
9. Тригонометрические функции кратногоаргумента
(cos i sin ) п cos п i sin п
cos i sin
п
cos n cos
n
n 1
i sin i sin
n
96. 7. Пример перехода от тригонометрической формы комплексного числа к алгебраической
10. Извлечение корня п-й степени изкомплексного числа
z r (cos i sin )
n
2 k
2 k
z r cos
i sin
n
n
n
k 0 ,1, , n 1
97. 8. Действия с комплексными числами в тригонометрической форме
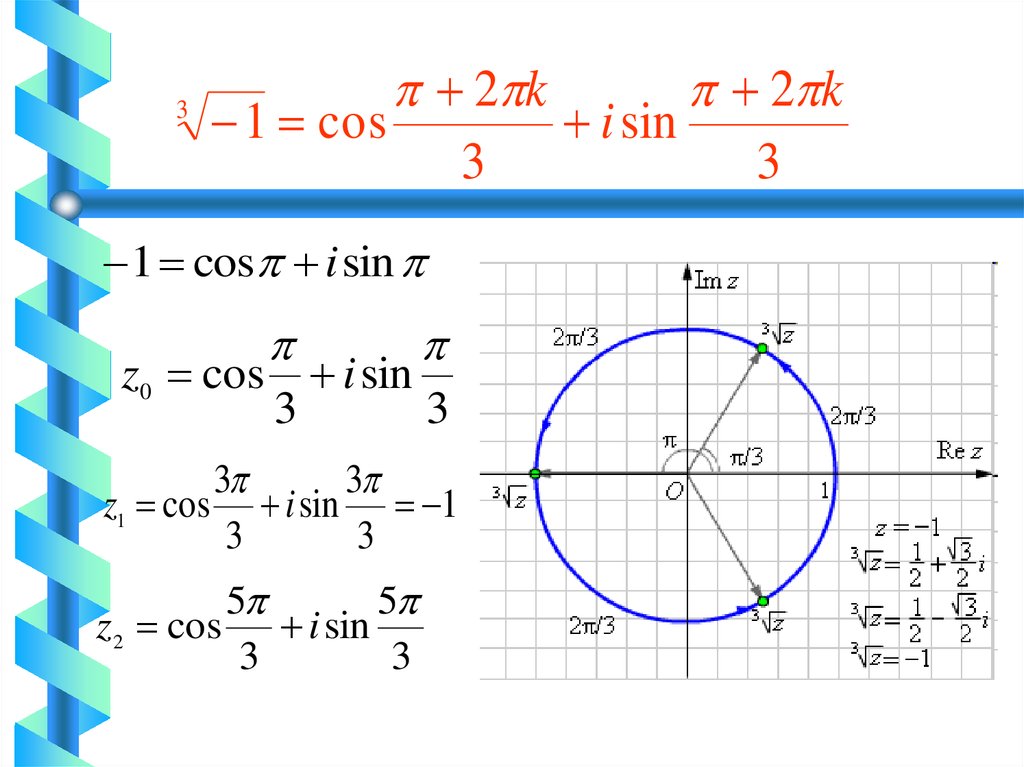
32 k
2 k
1 cos
i sin
3
3
1 cos i sin
z0 cos i sin
3
3
3
3
z1 cos i sin 1
3
3
5
5
z2 cos i sin
3
3
98. 9. Тригонометрические функции кратного аргумента
Алгебраические уравненияax+b=0
ax2+bx+c=0
ax3 +
bx2 + cx + d=0
ax4 + bx3 + cx2 + dx + е =0
99. 10. Извлечение корня п-й степени из комплексного числа
Алгебраические уравненияx3 +
6x2 + 6x +5=0
x3 + 3x2 – 9x +5=0
x3 – 6x + 4 = 0
x3 + 12x – 16i = 0
100.
Метод Феррариax4 +
bx3 + cx2 + dx + е =0
3_4 deg.doc



















































































 Математика
Математика








