Big data: технологии добычи данных

1. BIG DATA: Технологии добычи данных Кравченко Ю.А.

2. Цель исследования

2
повышение эффективности
прикладных систем добычи данных
на основе развития моделей,
методов и алгоритмов
семантического поиска,
классификации, кластеризации,
структурирования и интеграции
данных.
SFedU

3. Объект и предмет исследования

3
Объект
исследования
процессы
добычи данных
в условиях big
data
Предмет исследования
теоретические основы
разработки моделей, методов и
алгоритмов добычи данных
www.sapr.favt.tsure.ru

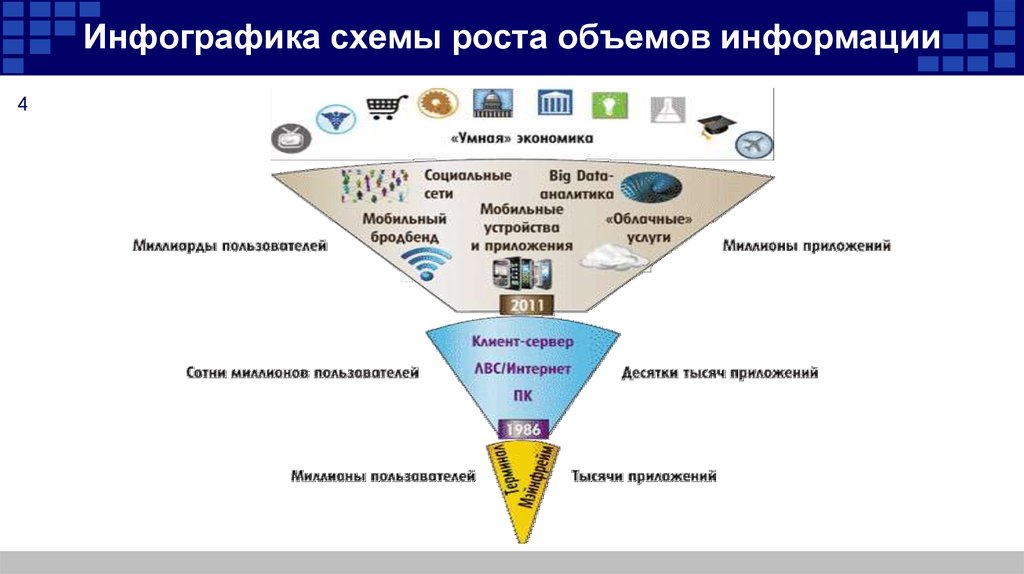
4. Инфографика схемы роста объемов информации

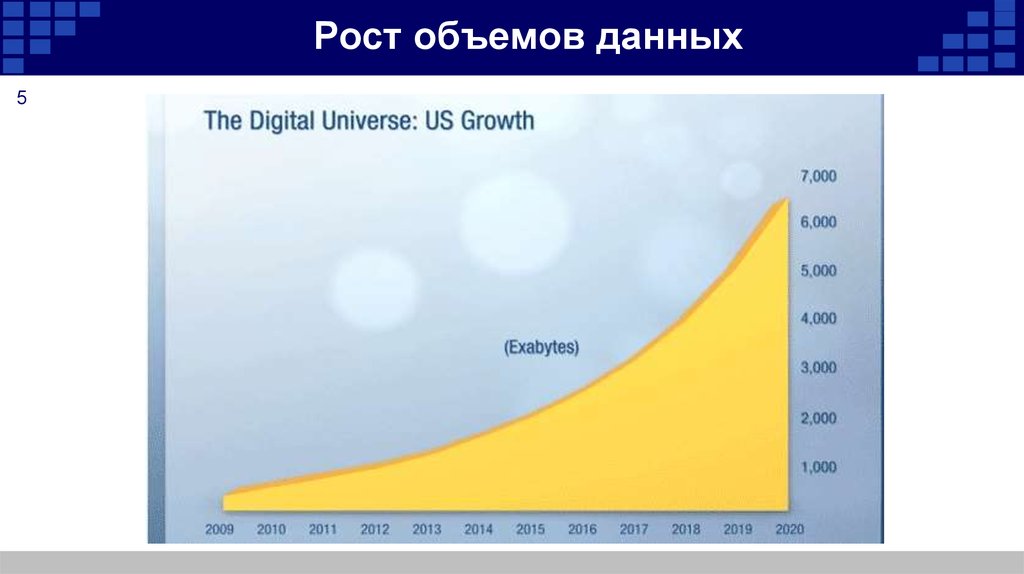
4

5. Рост объемов данных

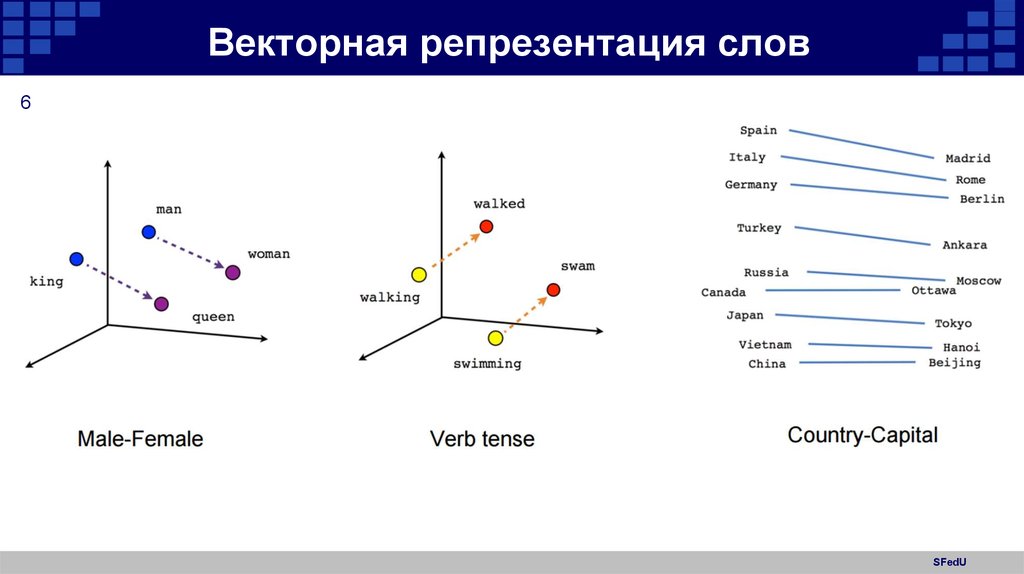
5

6. Векторная репрезентация слов

6
SFedU

7. Векторная репрезентация слов

7
SFedU

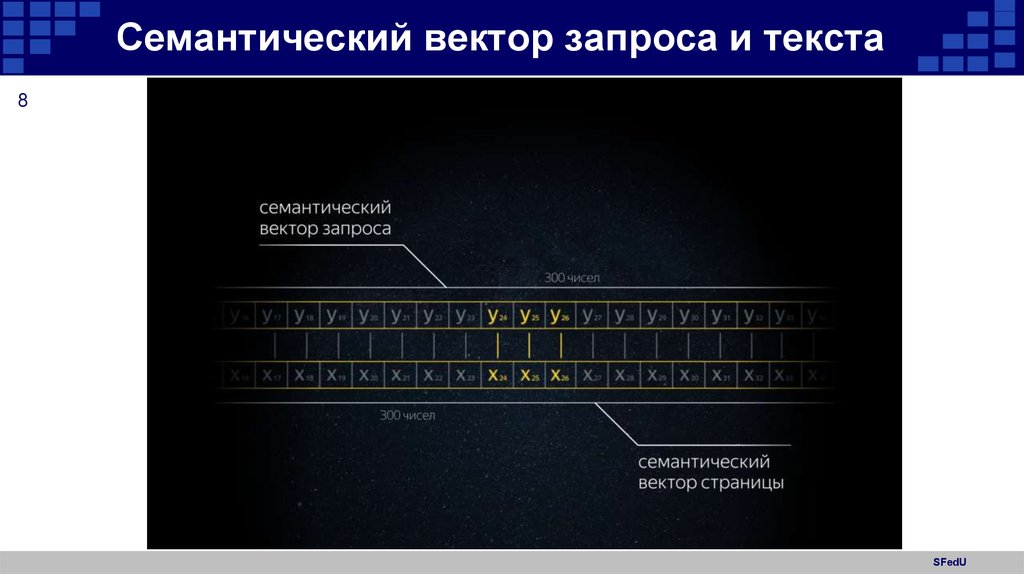
8. Семантический вектор запроса и текста

8
SFedU

9. Постановка задачи семантического поиска

9
Идея семантического поиска заключается в описании поисковых запросов в
виде набора триплетов. Пусть имеется запрос q, состоящий из набора
триплетов T(q). В таком случае результатом поиска в источнике знаний будет
набор элементов знания E = {ei │ i ϵ [1,k]}, где k – количество элементов
знания ei, являющихся результатом поиска. Причем, семантические
метаданные набора элементов знания Т(е) должны удовлетворять
следующему условию семантической близости sim(T(q),T(e)) с описанием
запроса T(q): sim(e,q) = sim(T(q),T(e)) > ε, где sim(e,q) близость запроса q и
элемента знания e, а ε – установленное пороговое значение релевантности.
Результаты поиска ранжируются по значениям их семантической близости к
запросу.
SFedU

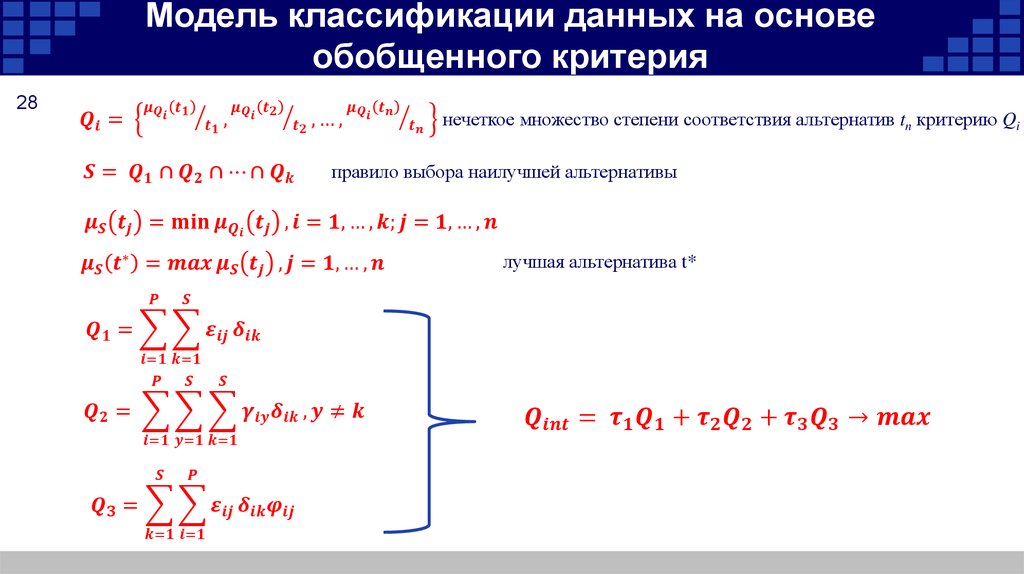
10. Постановка задачи классификации

10
Пусть
наименований
– множество описаний элементов знаний,
классов.
отображение
Существует
неизвестная
целевая
зависимость
–
, значения которой известны только на объектах
конечной обучающей выборки
построить алгоритм
объект
– множество
. Требуется
, способный классифицировать произвольный
.
Представим вероятностную постановку задачи классификации знаний,
которая считается более общей. Предполагается, что множество пар «элемент
знания,
класс»
является
с неизвестной вероятностной мерой
пространством
. Имеется конечная обучающая выборка
наблюдений
вероятностной мере
вероятностным
,
сгенерированная
. Требуется построить алгоритм
классифицировать произвольный объект
согласно
, способный
.
SFedU

11. Постановка задачи структуризации

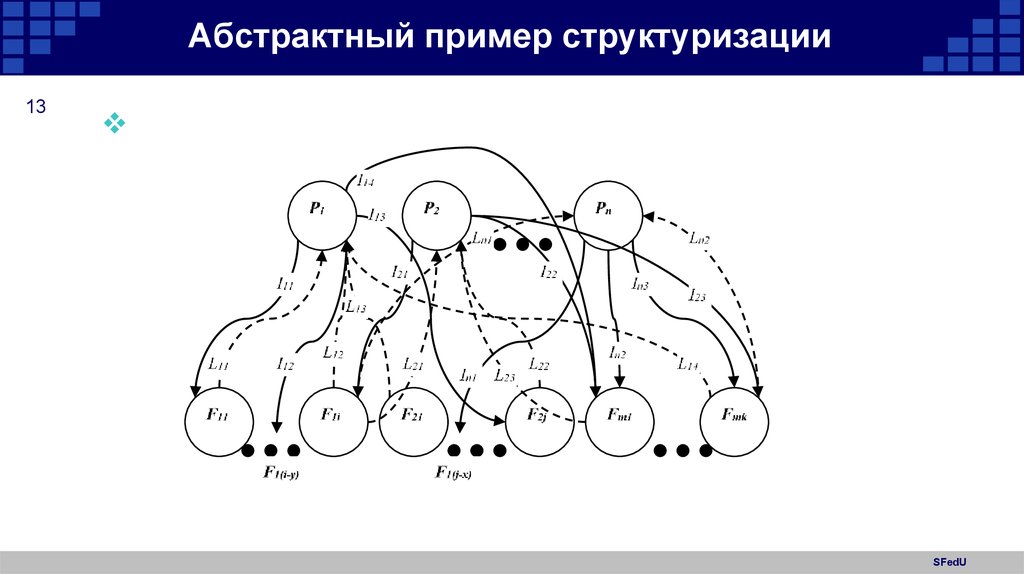
11
Все системно значимые признаки элементов знания из определенной предметной
области разобьем на m классов. Сформируем множество необходимых признаков
системной значимости F F F ... F .
1
2
m
F1 = {f11, f12,…, f1(i-1), f1i},
где f11, f12,…, f1(i-1), f1i – элементы множества F1, задающие 1-ый класс системно значимых
признаков для элементов знания некоторой предметной области;
F2 = {f21, f22,…, f2(j-1), f2j},
где f21, f22,…, f2(j-1), f2j – элементы множества F2, задающие 2-ой класс системно значимых
признаков для элементов знания некоторой предметной области;
Fm = {fm1, fm2,…, fm(k-1), fmk},
где fm1, fm2,…, fm(k-1), fmk – элементы множества Fm, задающие m класс системно значимых
признаков для элементов знания некоторой предметной области.
SFedU

12. Постановка задачи структуризации

12
Зададим для каждого анализируемого элемента знания qz (z = 1…n) множество
имеющихся у него системно значимых признаков Qz {Q11 Q12 ... Qnm} , где
Q
11
F1 , Q F 2 , Q F m
12
nm
.
Тогда выражение определения соответствия элемента знания системно значимым
требования предметной области представим в виде:
M Q F .
0
z
А целевая функция в таком случае примет вид:
M F .
0
Отсутствие заданного тождества указывает на неполное соответствие элемента
требованиям, выдвигаемым к системно значимым признакам.
SFedU

13. Абстрактный пример структуризации

13
SFedU

14. Постановка задачи интеграции

14
Представим постановку задачи системной интеграции знаний множества онтологий в виде
следующего выражения: