Похожие презентации:
Релейная защита в распределительных электрических сетях
1.
IK,AK
A
IK,B
B
N
IK,C
IK,B
N
IA ≈ 0
A
K
B
IK,C
C
N
IK,C
IA3
A
K
B
C
B
IC ≈ 0
C
K(1)
K
б)
в)
A
IA ≈ 0
IK,B
B
N
K1
N
C
IK,C
K2
K(1.1`)
г)
A
IB ≈ 0
C
а)
IK,B
N
K
K(2)
K(3)
IA≈0
IK,A
д)
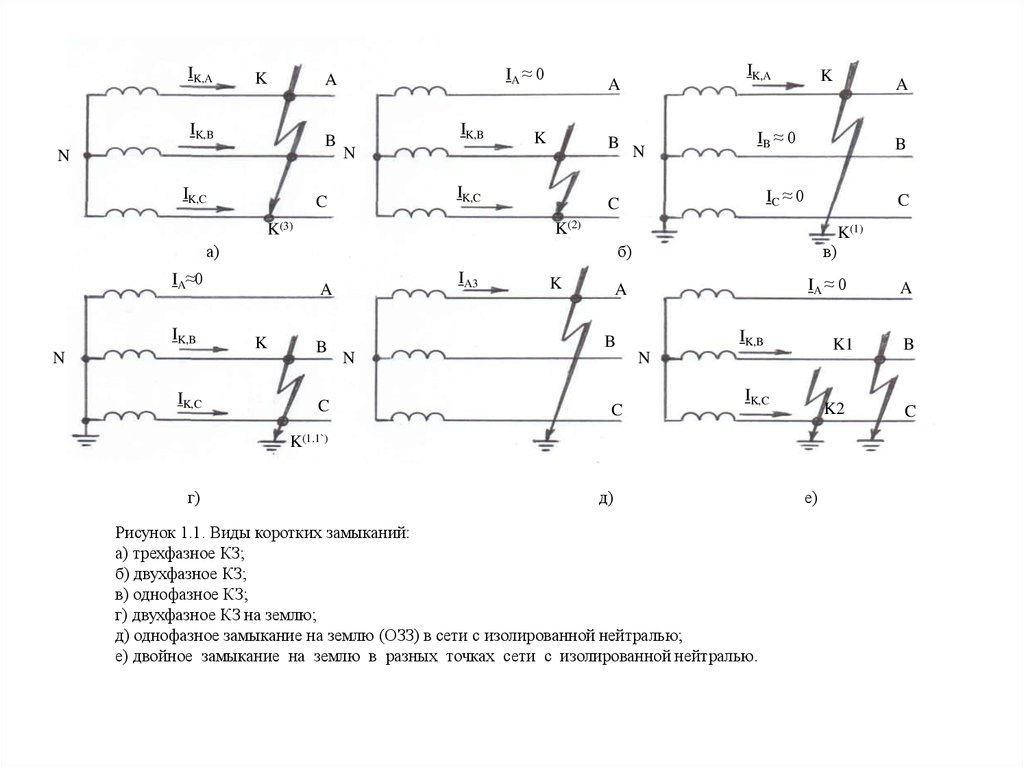
Рисунок 1.1. Виды коротких замыканий:
а) трехфазное КЗ;
б) двухфазное КЗ;
в) однофазное КЗ;
г) двухфазное КЗ на землю;
д) однофазное замыкание на землю (ОЗЗ) в сети с изолированной нейтралью;
е) двойное замыкание на землю в разных точках сети с изолированной нейтралью.
е)
A
B
C
2.
EUост,1
Zс
G
Uост,2
L
1
Zл
K2
K1
Рисунок 1.2. Зависимость остаточного напряжения на шинах
подстанции 1 от удаленности точки КЗ
U ост I к Z л ,
Iк
- ток короткого замыкания, протекающий на участке сети от шин подстанции 1 до точки К;
Zл
- полное сопротивление участка сети от шин подстанции до точки К.
3.
12
5
4
3
G
a)
Iг
Iн
Iл
2
Xл
Хг
E
4
3
5
Хн
Rл
1
UΣ
Uн
Uл + Uн
б)
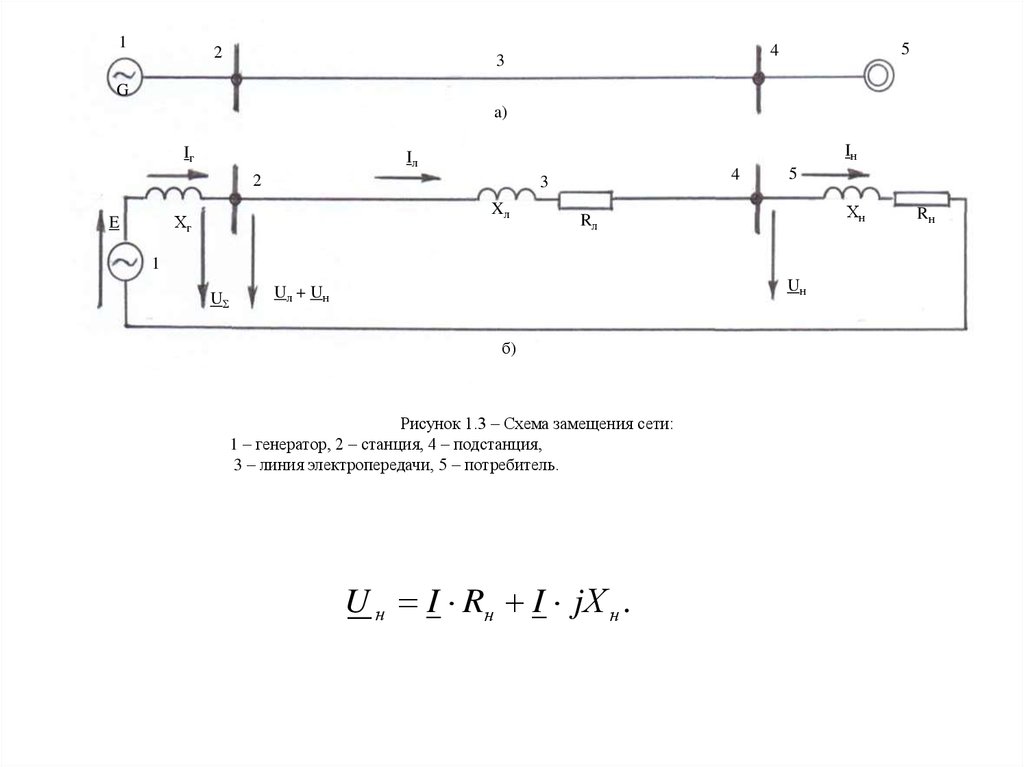
Рисунок 1.3 – Схема замещения сети:
1 – генератор, 2 – станция, 4 – подстанция,
3 – линия электропередачи, 5 – потребитель.
U н I Rн I jХ н .
Rн
4.
I·jХгI·jХл
Uг
Uл
UΣ
н arctg
.
I
φл
Хн
Rн
(1.4)
I·jХн
Uн
I·Rн
.
φс
л ,н arctg
φлн
Хн Хл
Rн R л
(1.5)
φн
Е
c arctg
Х. г Х л Х н
R л Rн
(1.6)
5.
АС
А1
а)
С1
120º
б)
а1, в1, с1 а
в1
1
А1
В2
120º
120º
180º
В
С2
В1
с1
t1
ωt
360º
а2, в2, с2
В2
А0
120º
А2
120º
в)
а2
180º
в2
В0
с2
ωt
а0, в0, с0
А0
t2 360º
Симметричные трехфазные системы:
а) исходная несимметричная система полных векторов;
б) прямая последовательность;
в) обратная последовательность;
г) нулевая последовательность.
г)
С0
ωt
6.
: а = еj120º+j
-1/2
или
а = -0,5 + j0,87
1·a
240º
120º
1
1
1 a 2 1 a 1 3 ( j)
или
1 3 a
2
j30
1·a2
1 1 a 1 3
2
j30
7.
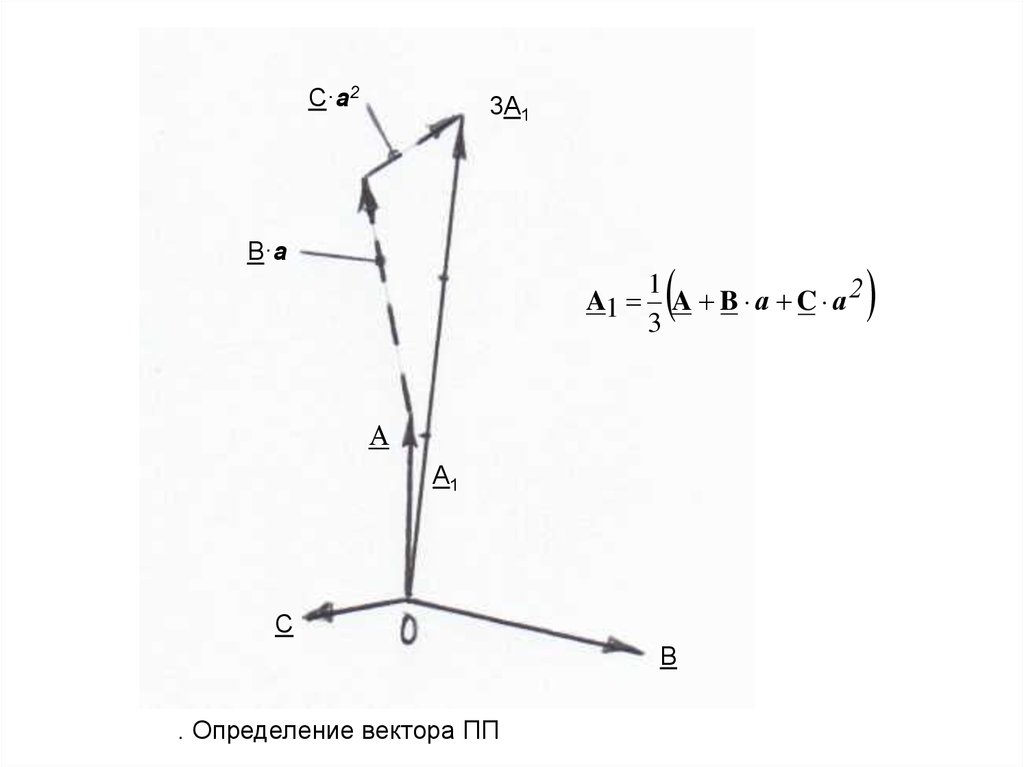
С·а23А1
В·а
A1
1
A B a C a2
3
А
А1
С
В
. Определение вектора ПП
8.
В·а2А
А
В
С
3А0
С·а
3А2
С
С
В
В
б)
а)
1
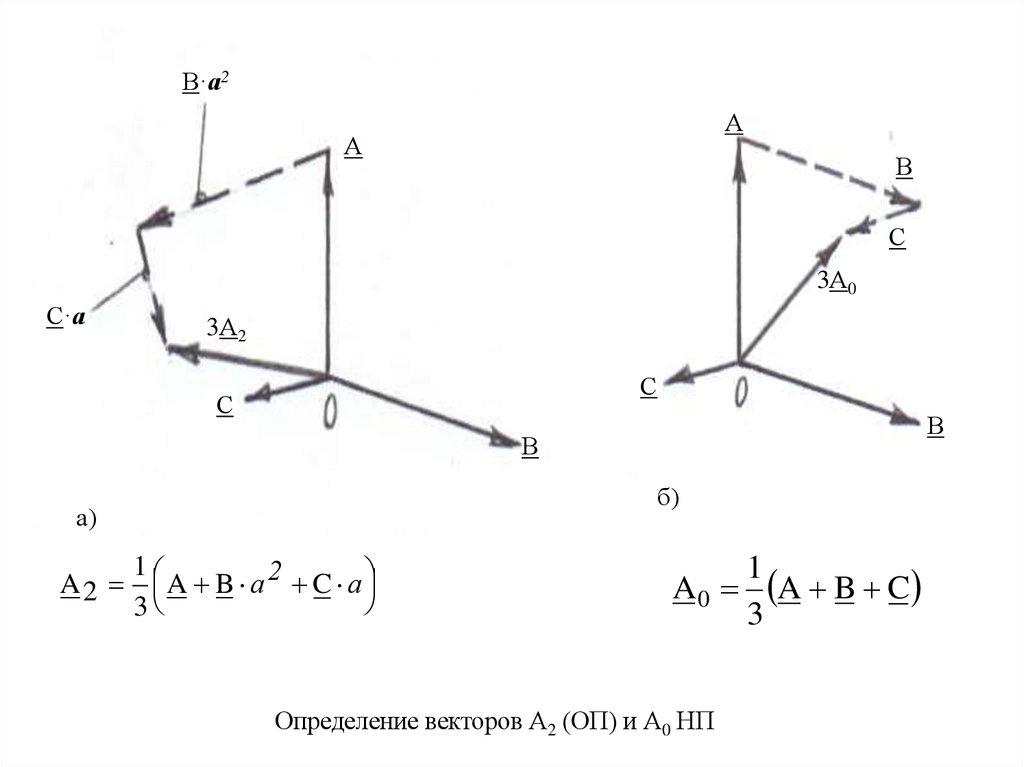
A 2 A B a 2 C a
3
1
A 0 A B C
3
Определение векторов А2 (ОП) и А0 НП
9.
1B2 B C a 2 A a
3
1
C 2 C A a 2 B a
3
1
A1 A B a C a 2
3
1
B1 B C a A a 2
3
1
C1 C A a B a 2
3
1
2
A 2 A B a C a
3
А0= В0= С0 = 1 ( А+ В + С )
3
10.
RАВ = А - В; ВС = В - С; СА = С - А.
А2
ВС·а
3А2
а
А = В + АВ
С = В - ВС
АВ
А
с
С
СА
В
3А1
ВС
в
А1
ВС·а2
р
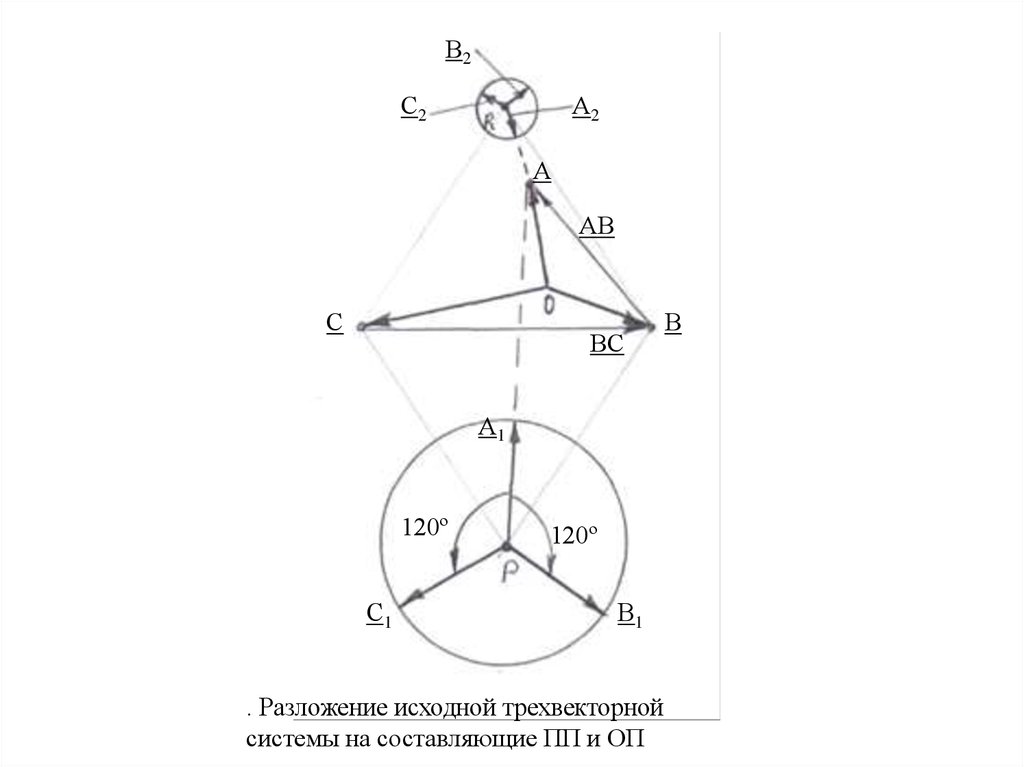
Разложение исходной трехвекторной
системы на составляющие ПП и ОП
11.
АВ = А - В; ВС = В - С; СА = С - А.С = В - ВС
А = В + АВ
1
1
2
A1 B AB B a (B BC) a B(1 a a 2 ) AB BC a 2
3
3
1
1
AB BC a 2 AB ( BC a 2 ) .
(2.14)
3
3
1
1
2
A 2 B AB B a (B BC) a (AB BC a)
3
3
12.
В2С2
А2
А
АВ
С
ВС
А1
120º
С1
120º
В1
. Разложение исходной трехвекторной
системы на составляющие ПП и ОП
В
13.
В2С2
А2
3А2
А
АВ
С
В
ВС
3А1
А1
С1
В1
. Разложение полных векторов
несимметричной трехвекторной системы на
составляющие ПП и ОП
14.
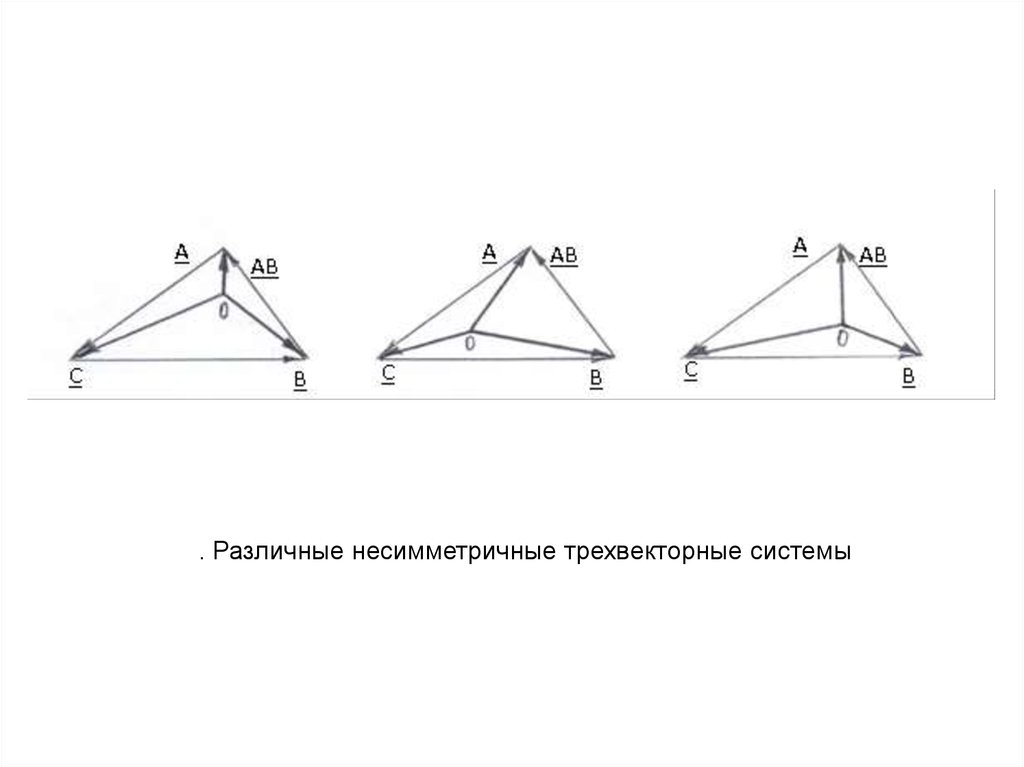
. Различные несимметричные трехвекторные системы15.
АА
А2 = 0
АВ
АВ
СА
С
ВС
В
А2 = 0
В
СА
ВС
С
А1
А1
а)
б)
Исходные трехфазные системы, не содержащие
составляющих ОП
16.
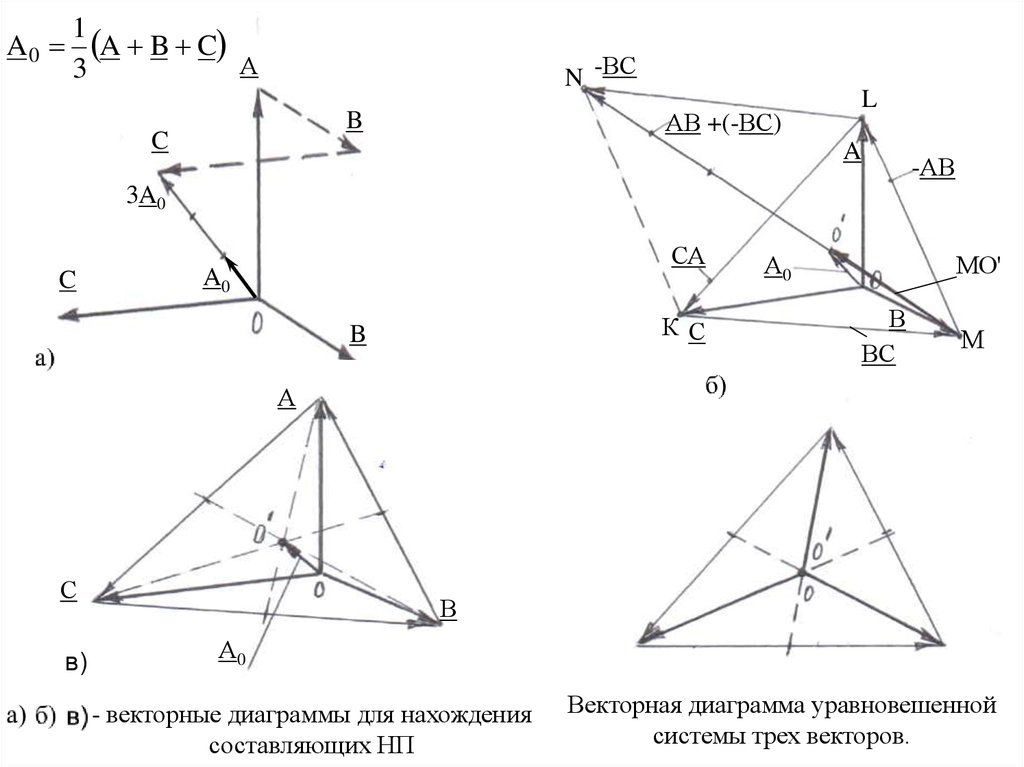
A01
A B C
А
3
N -ВС
C
L
АВ +(-ВС)
B
A
-АВ
3A0
C
СА
A0
КС
B
А0
МО'
В
ВС
М
А
С
в)
В
А0
- векторные диаграммы для нахождения
составляющих НП
Векторная диаграмма уравновешенной
системы трех векторов.
17.
А = В + АВA0
С = В - ВС
1
A B C 1 B AB B B BC B 1 (AB BC)
3
3
3
18.
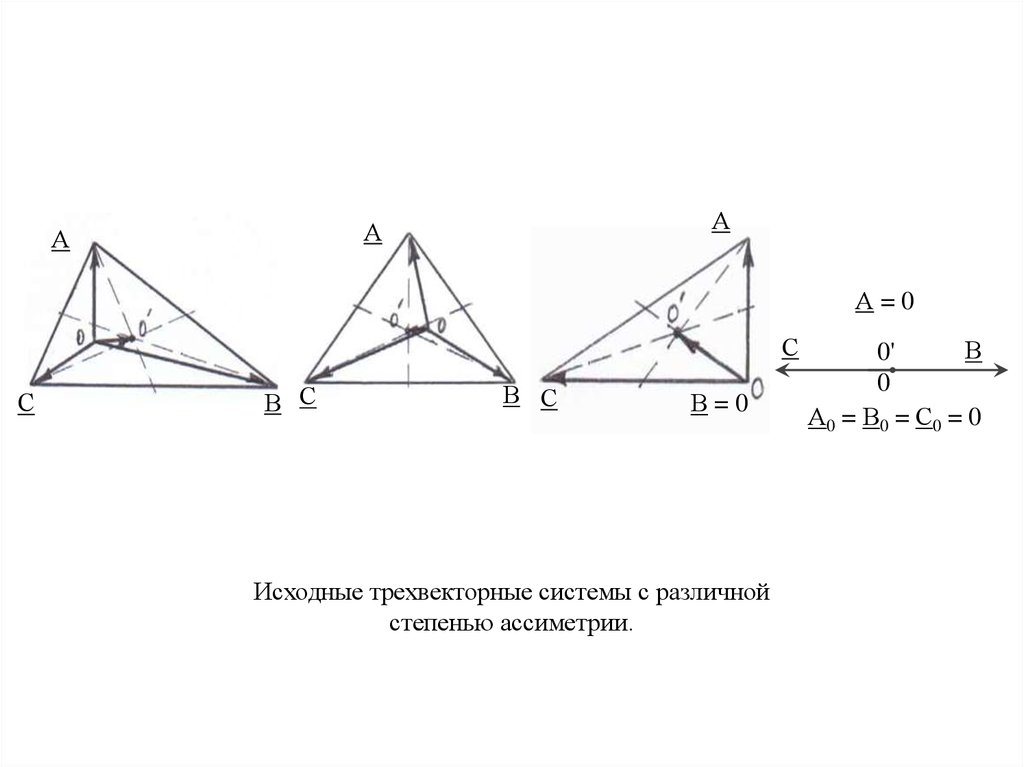
АА
А
А=0
С
С
В С
В С
В=0
Исходные трехвекторные системы с различной
степенью ассиметрии.
В
0'
0
А0 = В0 = С0 = 0
19.
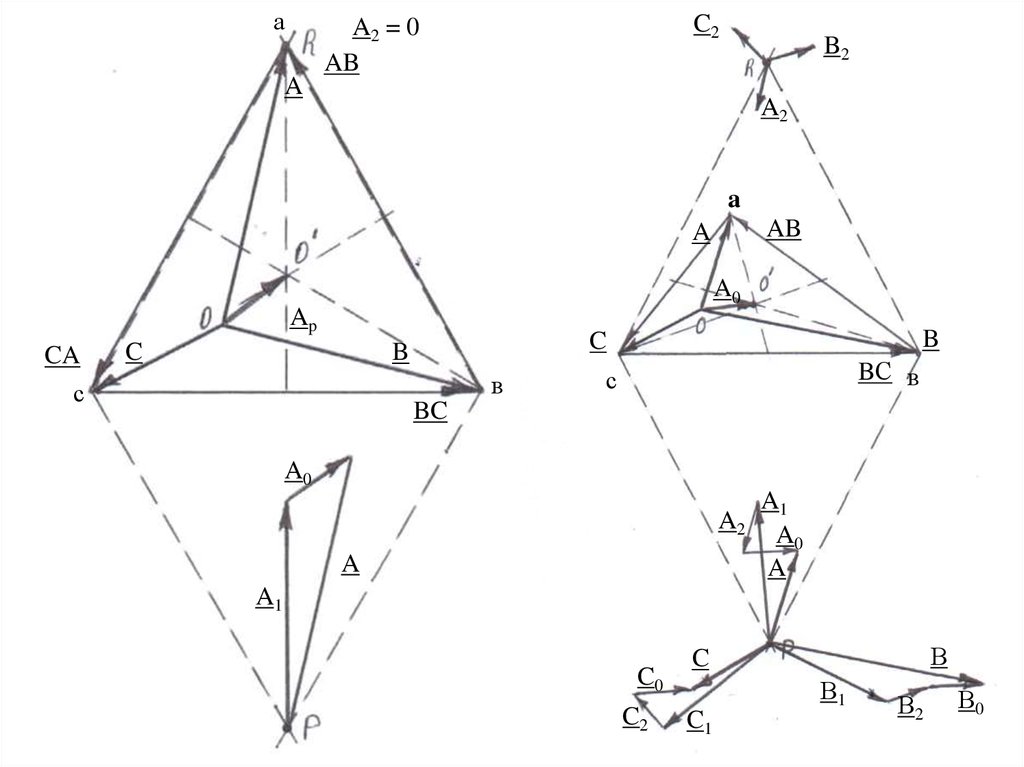
аC2
A2 = 0
AB
B2
A
A2
a
AB
A
A0
Ap
CA
с
C
B
C
B
в
BС в
с
BC
A0
A2
A
A1
A0
A
A1
C0
C2
В
C
В1
C1
В2
В0




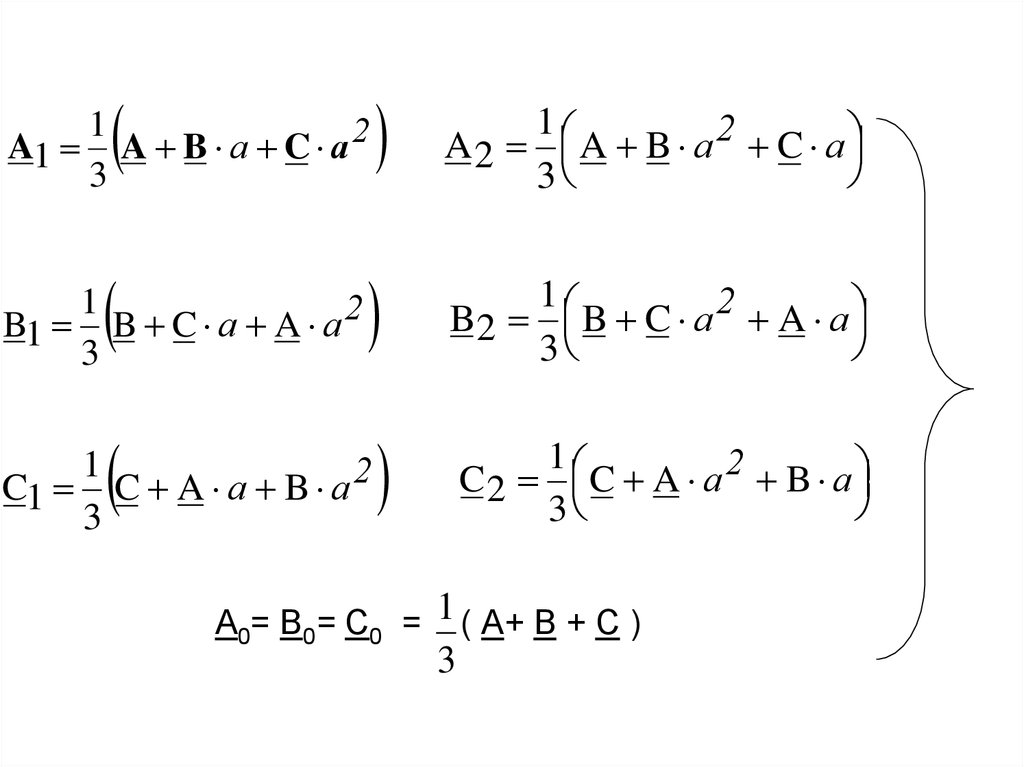





 Электроника
Электроника Промышленность
Промышленность