Современные методы статистического анализа кадастровых данных

1. Землеустроительныйфакультет

Землеустроительн
ыйфакультет
дисциплина:
Современные методы
статистического анализа
кадастровых данных
к.э.н., профессор кафедры землеустройства и земельного
кадастра
Яроцкая Елена Вадимовна
1

2.

3 Оценка параметров качества математической модели
Оценка параметров качества математической модели на примере в Excel
Пример 1
Для построения статистической модели расчета кадастровой стоимости
ОКС оценочной группы города «Морское побережье» было подобрано 385
объектов аналогов с одним ценообразующим фактором, которые
представлены в таблице в Excel
Необходимо:
1) провести корреляционный анализ;
2) построить парную регрессионную модель;
3) провести регрессионный анализ;
4) построить нелинейные регрессионные модели;
5) проверить качество построенных моделей.
2

3.

3

4.

1) корреляционный анализ
Построим корреляционное поле для предварительного изучения
взаимосвязи результативного признака и ценообразующего фактора.
Меню «Вставка» → «Точечная»
4

5.

График, отражающий визуальную зависимость показателя (Удельная цена,
(Y)) и ценообразующего фактора (Расстояние объекта до центра населенного
пункта, м (X)).
8 000
7 000
6 000
5 000
4 000
3 000
2 000
1 000
0
0
10000
20000
30000
40000
50000
60000
70000
80000
90000
-1 000
-2 000
5

6.

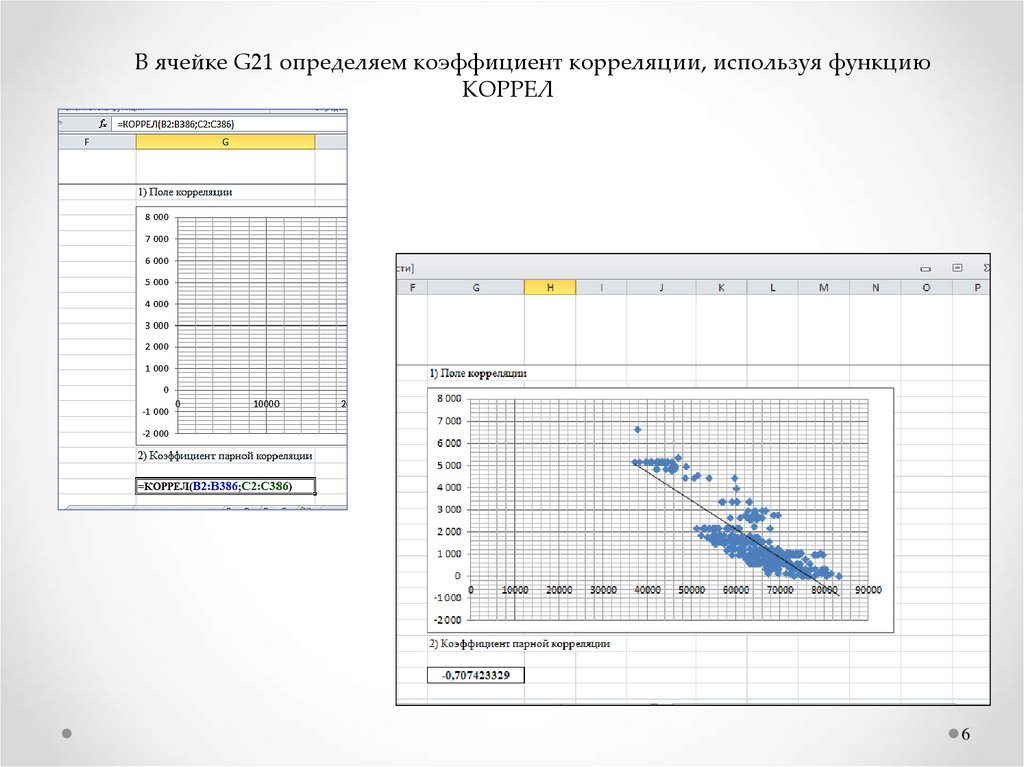
В ячейке G21 определяем коэффициент корреляции, используя функцию
КОРРЕЛ
6

7.

ВЫВОД:
Корреляция отрицательная, по шкале
Чеддока имеет заметную силу связи между
результативной и факторной переменной.
Это означает, что с увеличением
расстояния от объекта оценки до центра
населенного пункта будет уменьшаться
удельная цена объекта недвижимости.
7

8.

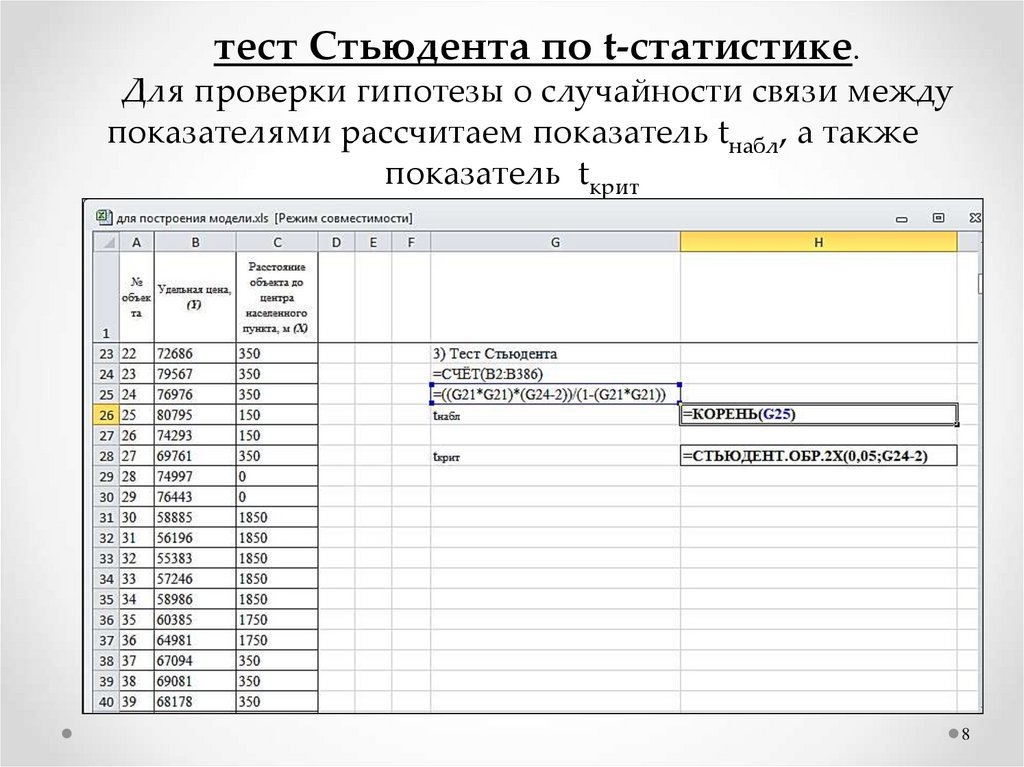
тест Стьюдента по t-статистике.
Для проверки гипотезы о случайности связи между
показателями рассчитаем показатель tнабл, а также
показатель tкрит
8

9.

показатели t-статистики
9

10.

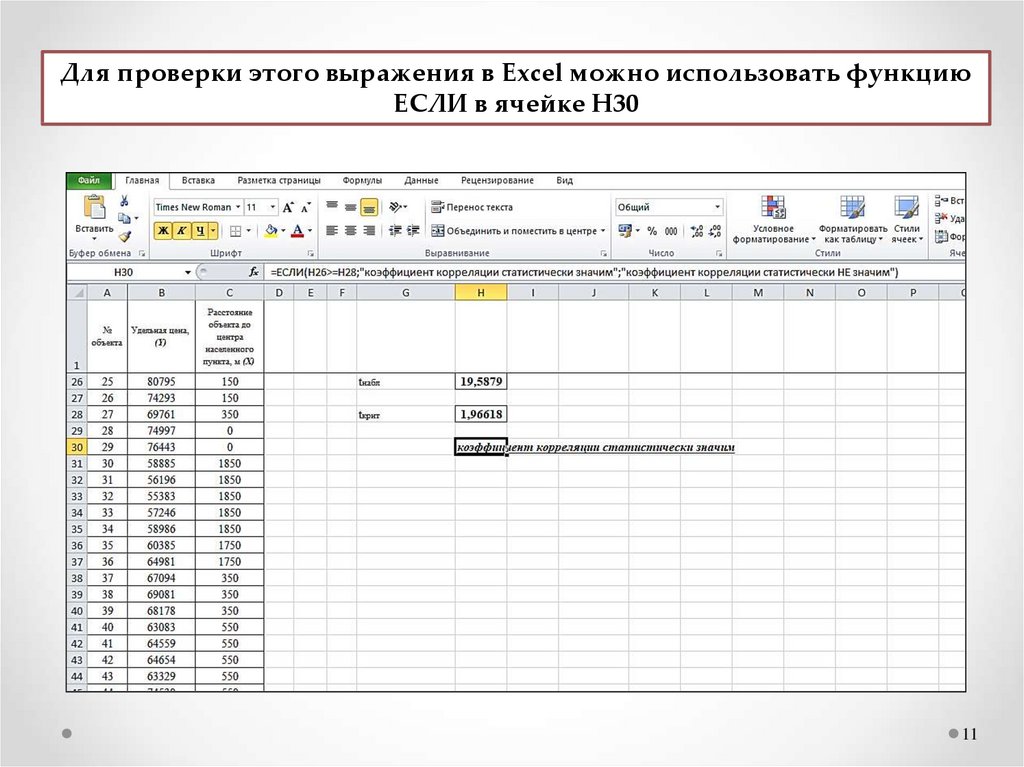
Таблица Стьюдента
Коэффициент корреляции признается статистически значимым, если
tнабл≥tкрит
В нашем случае, это правило выполняется.
10

11.

Для проверки этого выражения в Excel можно использовать функцию
ЕСЛИ в ячейке Н30
11

12.

Общий вывод по корреляционному
парному анализу:
теснота связи между
ценообразующим фактором
«Расстояние от объекта оценки до
центра населенного пункта» и
результативной переменной
«Удельная цена» доказана и
значительна.
12

13.

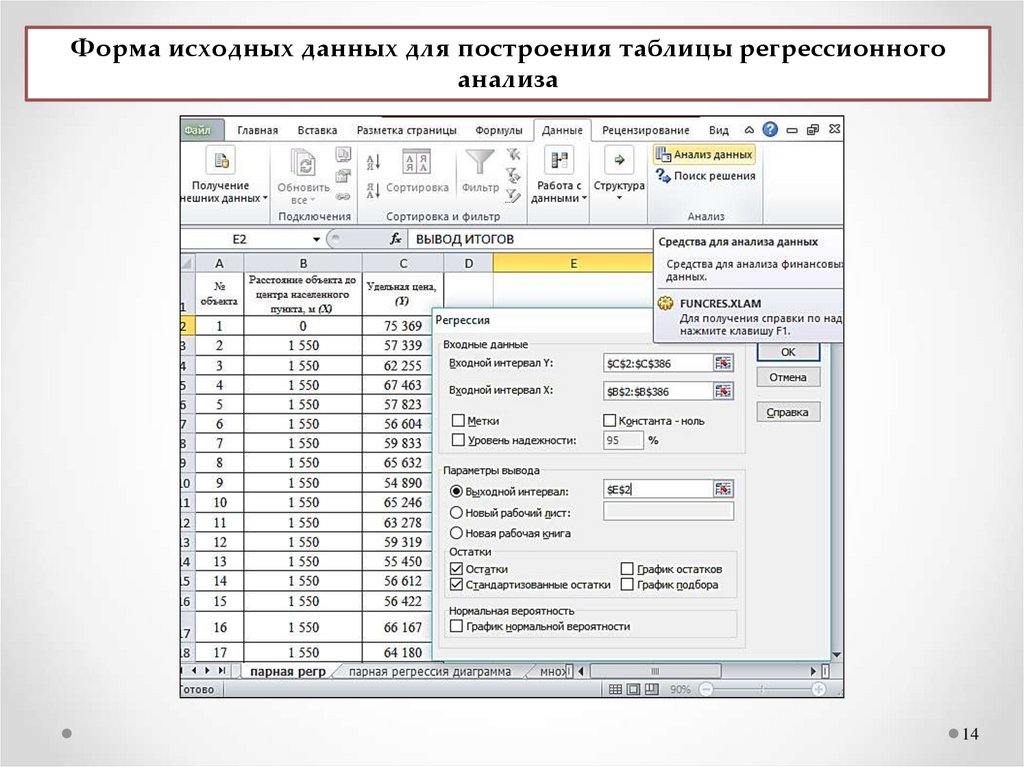
2) построение парной регрессионной модели
Для построения линейной модели парной регрессии используем
инструмент Регрессия пакета Анализ данных в MS Excel.
13

14.

Форма исходных данных для построения таблицы регрессионного
анализа
14

15.

Таблица парного регрессионного анализа
15

16.

Множественный R –коэффициент корреляции
R-квадрат (индекс детерминации) равен 0,50044777 – это среднее
значение данного показателя. R-квадрат означает, что удельная
цена объектов недвижимости на 50% объясняет зависимость от
расстояния от объекта оценки до центра населенного пункта. Чем
выше коэффициент детерминации, тем качественнее модель.
Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли
можно считать резонным).
16

17.

уравнение парной регрессии принимает вид
ВЫВОД: Модель показывает, что с увеличением
расстояния от объекта недвижимости до центра
населенного пункта на 1 м удельная цена объекта
недвижимости уменьшится на 4,76 руб.
17

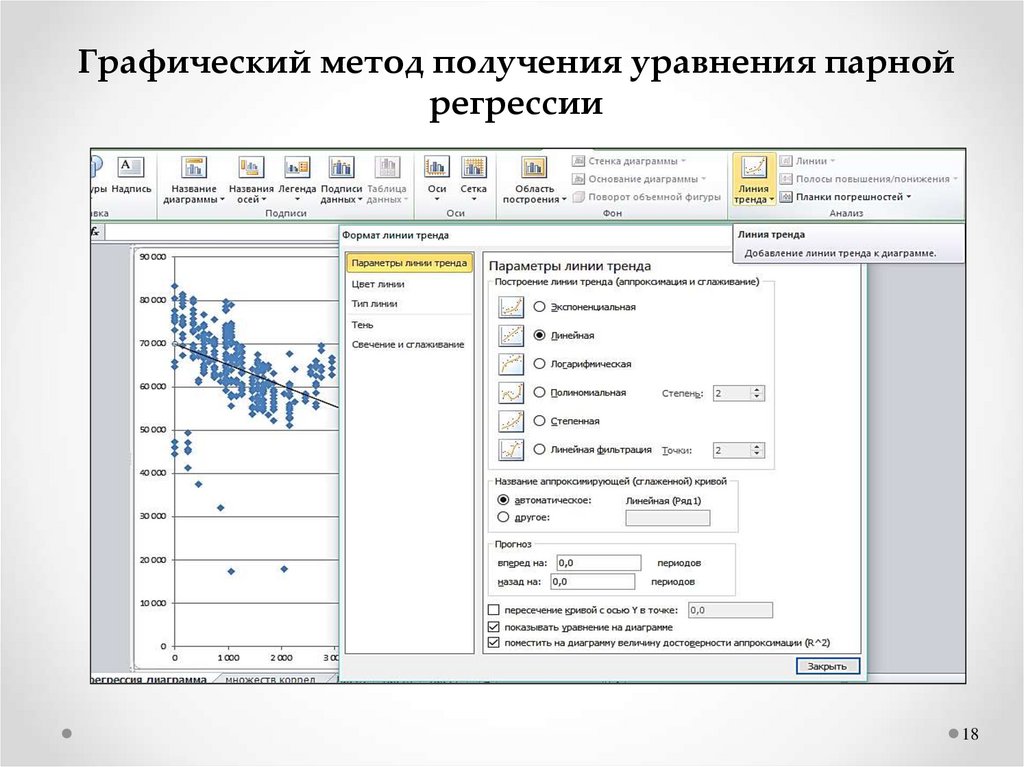
18.

Графический метод получения уравнения парной
регрессии
18

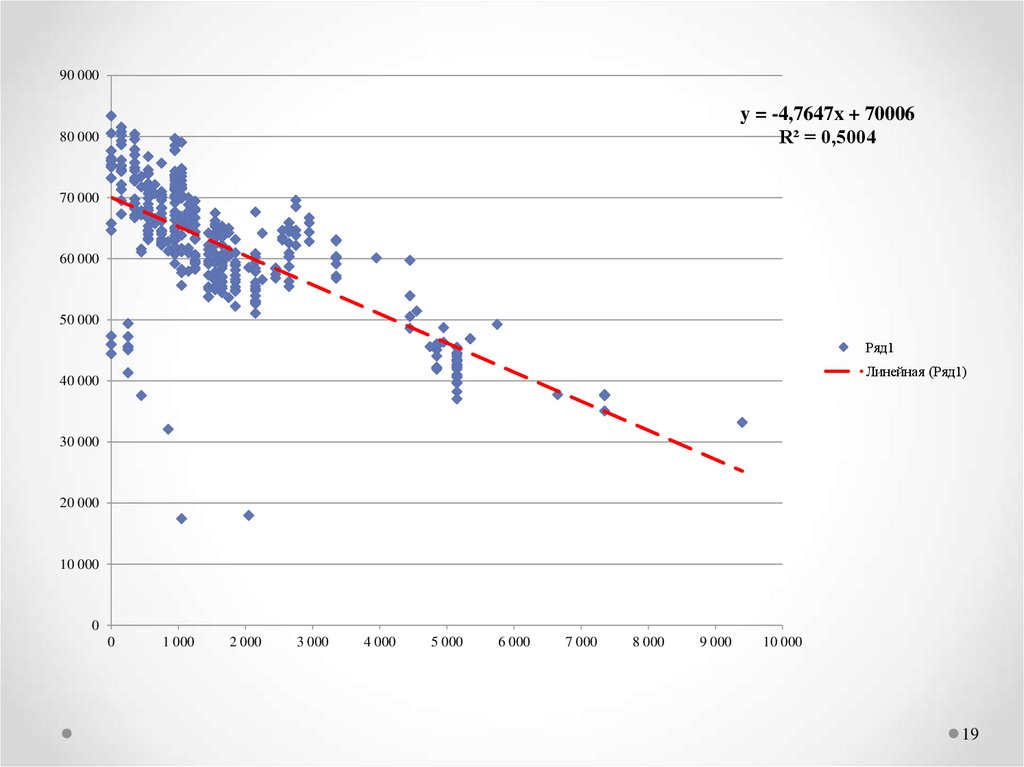
19.

90 000
y = -4,7647x + 70006
R² = 0,5004
80 000
70 000
60 000
50 000
Ряд1
Линейная (Ряд1)
40 000
30 000
20 000
10 000
0
0
1 000
2 000
3 000
4 000
5 000
6 000
7 000
8 000
9 000
10 000
19

20.

а) Столбец «df» – число степеней свободы (используется при проверке
адекватности модели по статистическим таблицам). В строке «Регрессия»
находится k1 – количество коэффициентов уравнения, не считая
свободного члена b; в строке «Остаток» находится k2 = n – k1 – 1, где n –
количество исходных данных.
б) Столбец «SS» (сумма квадратов);
в) Столбец «MS» – вспомогательные величины:
г) Столбец «F» – критерий Фишера. Используется для проверки
адекватности модели;
д) Столбец «Значимость F» – оценка адекватности построенной модели.
Если значимость F меньше 0,05, то модель может считаться адекватной с
вероятностью 0,95.
20

21.

е) «Стандартная ошибка», «t-статистика» – это вспомогательные величины,
используемые для проверки значимости коэффициентов модели.
все показатели соответствуют правилу
Коэффициент tкрит определялся в корреляционном анализе
ж) «Р-Значение» – оценка значимости коэффициентов модели. Если «РЗначение» меньше 0,05, то с вероятностью 0,95 можно считать, что
соответствующий коэффициент модели значим (т.е. его нельзя считать
равным нулю и Y значимо зависит от соответствующего Х).
и) Нижние и верхние 95% – доверительные интервалы для коэффициентов
модели.
Общий вывод: построенная модель адекватна, коэффициенты уравнения
парной регрессии значимы.
21

22.

3) построить нелинейные регрессионные модели
степенная,
логарифмическая,
полиномная,
экспоненциальная
Построение графической
линии тренда
22

23.

Нелинейные модели парной регрессии
90 000
y = -4,7647x + 70006
R² = 0,5004
80 000
y = 70390e-9E-05x
R² = 0,4578
70 000
y = 7E-05x2 - 5,2225x + 70393
R² = 0,501
60 000
Ряд1
Линейная (Ряд1)
50 000
Экспоненциальная (Ряд1)
Полиномиальная (Ряд1)
Полиномиальная (Ряд1)
40 000
Степенная (Ряд1)
Степенная (Ряд1)
Логарифмическая (Ряд1)
30 000
y = 67359x-0,016
R² = 0,0614
20 000
y = -2E-17x6 + 5E-13x5 - 5E-09x4 + 2E-05x3 - 0,0323x2 + 15,432x + 67680
R² = 0,5349
10 000
y = -981ln(x) + 68153
R² = 0,0814
0
0
1 000
2 000
3 000
4 000
5 000
6 000
7 000
8 000
9 000
10 000
23

24.

Пример 2
Для построения статистической модели расчета кадастровой стоимости
ОКС оценочной группы города «Морское побережье» было подобрано 385
объектов аналогов со множеством ценообразующих факторов, которые
представлены в таблице
Необходимо:
1) провести корреляционный анализ;
2) построить множественную регрессионную модель;
3) провести регрессионный анализ;
4) построить нелинейные регрессионные модели;
5) проверить качество построенных моделей.
Корреляционно-регрессионый множественный линейный анализ
проводится по аналогии с парным анализом.
24

25.

Входная информация для моделирования
25

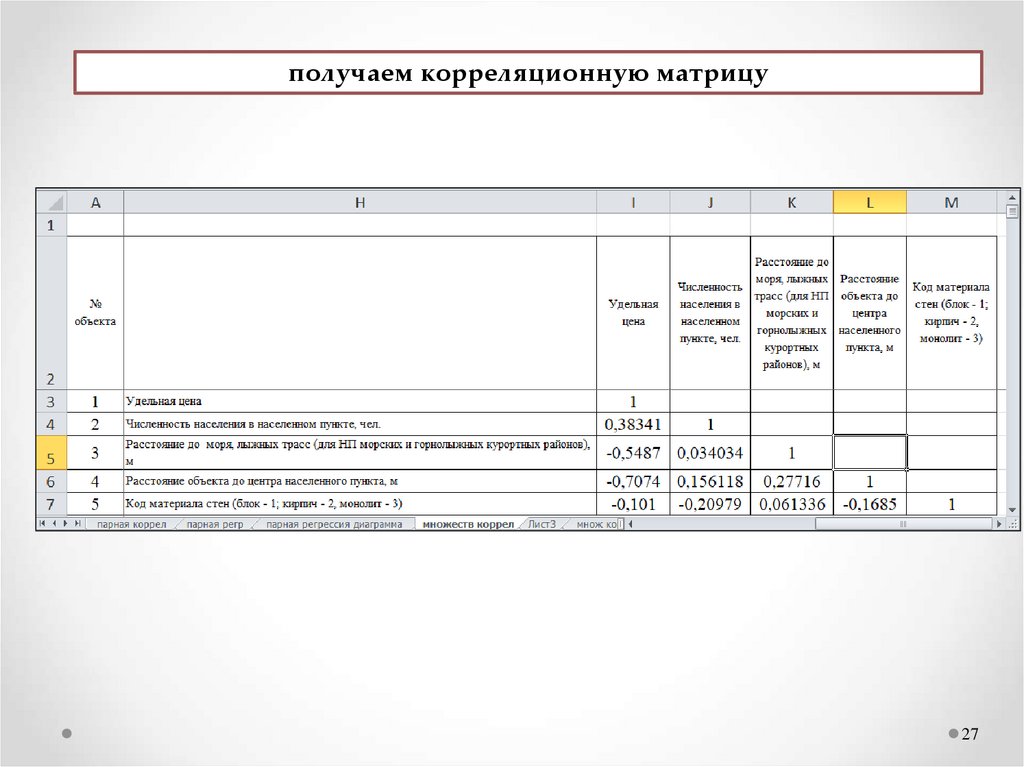
26.

1) корреляционный анализ
частные коэффициенты корреляции рассчитываются путем построения
корреляционной матрицы Анализ данных → Корреляция
26

27.

получаем корреляционную матрицу
27

28.

Таблица множественного линейного регрессионного
анализа
28

29.

Анализ таблицы множественного линейного
регрессионного анализа происходит
аналогично парному линейному
регрессионному анализу
Общий вывод: построенная модель адекватна,
коэффициенты уравнения парной регрессии
значимы.
29

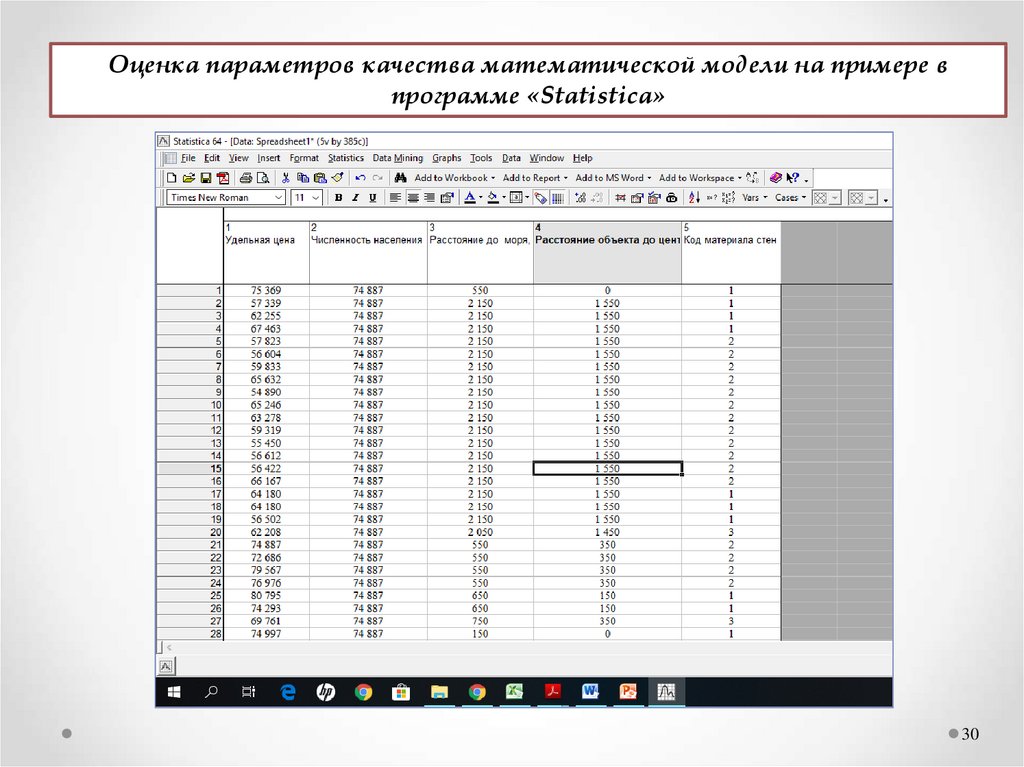
30.

Оценка параметров качества математической модели на примере в
программе «Statistica»
30

31.

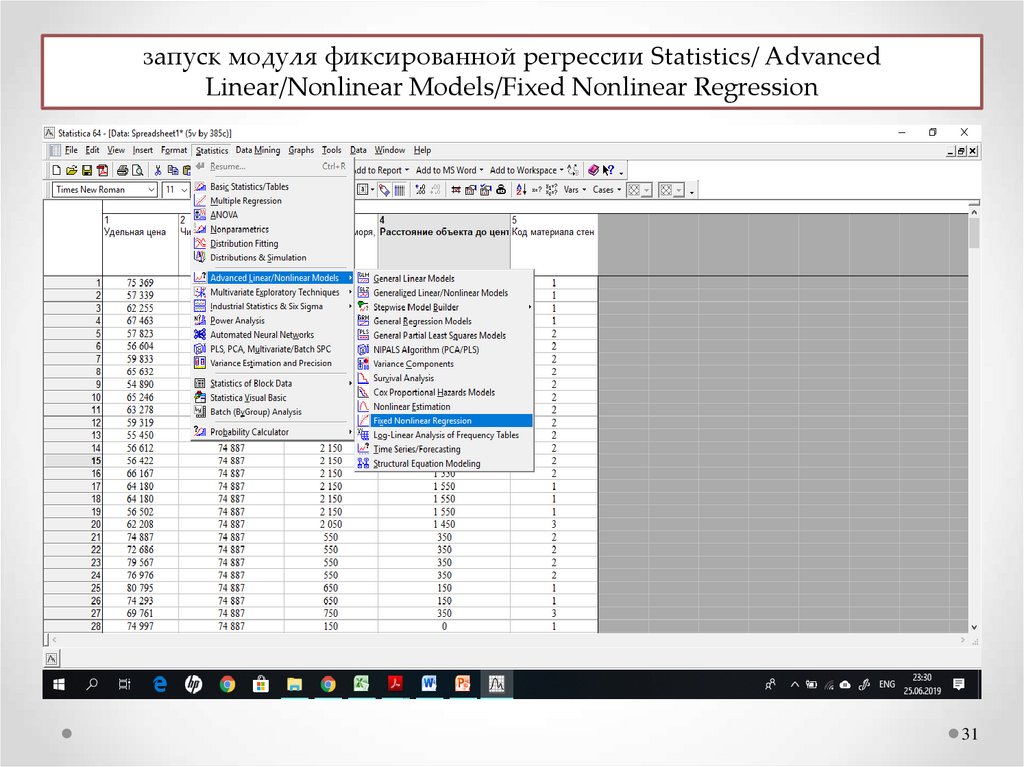
запуск модуля фиксированной регрессии Statistics/ Advanced
Linear/Nonlinear Models/Fixed Nonlinear Regression
31

32.

В диалоговом окне Non-linear Components Regression выбираются типы
нелинейных моделей
32

33.

Получаем результаты
33

34.

Оценка параметров качества математической модели на примере в
программе «Массовая оценка»
34

35.

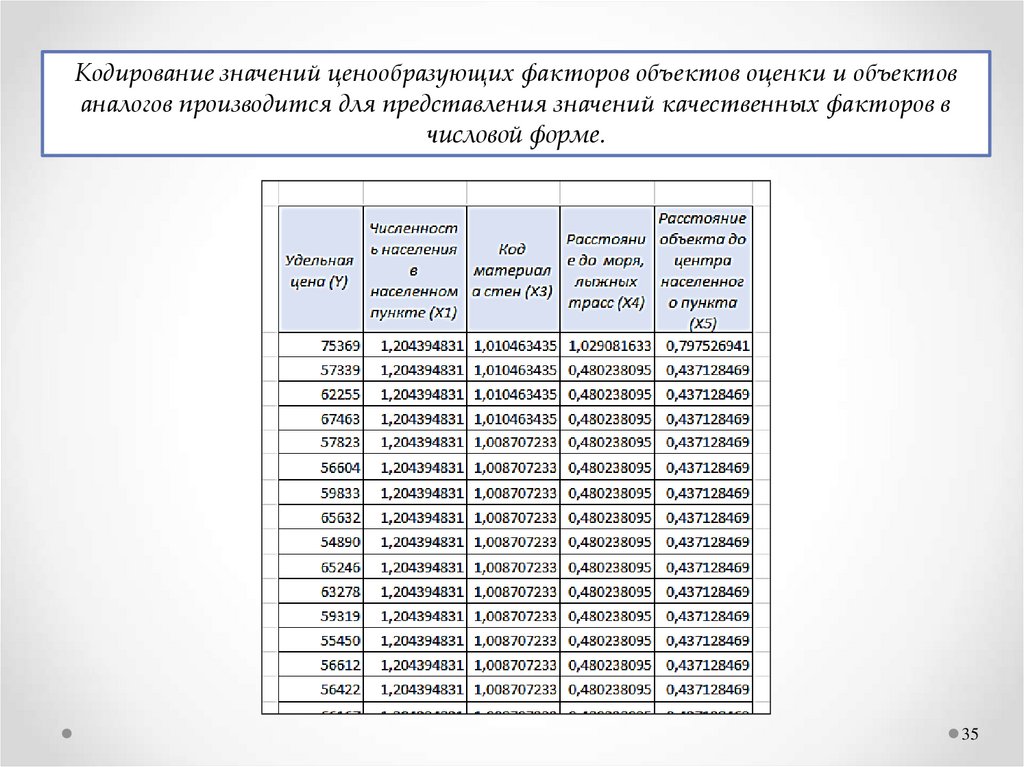
Кодирование значений ценообразующих факторов объектов оценки и объектов
аналогов производится для представления значений качественных факторов в
числовой форме.
35

36.

Скриншот рабочего поля ПК «Массовая Оценка» по расчету коэффициентов
корреляции
36

37.

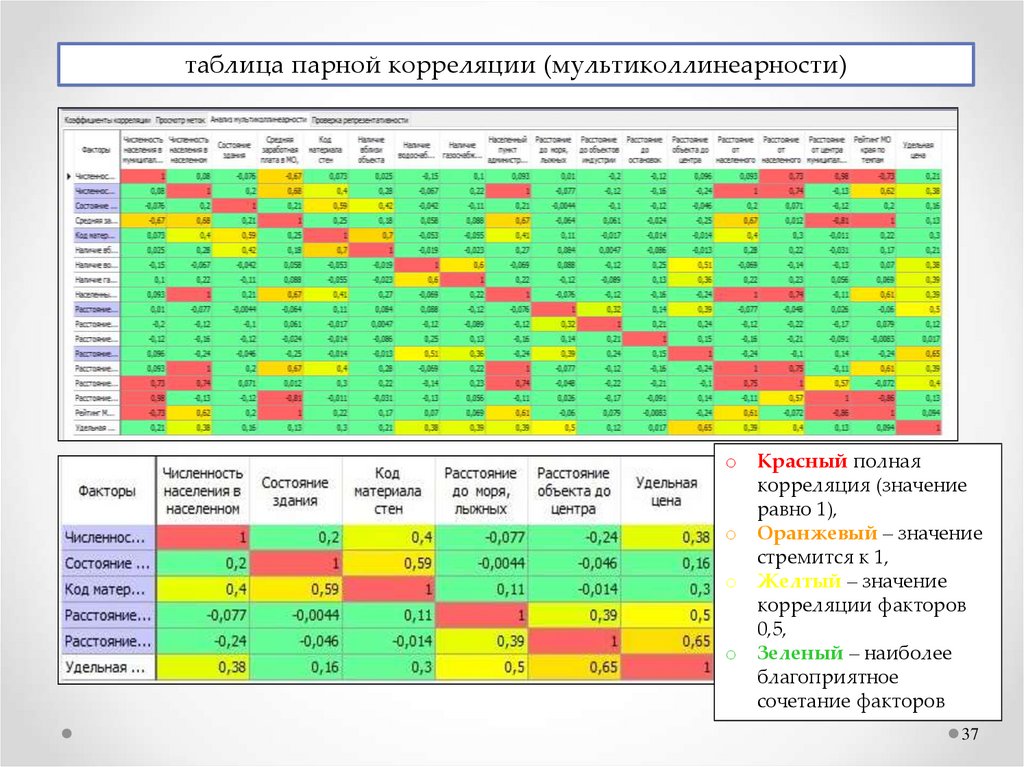
таблица парной корреляции (мультиколлинеарности)
o
o
o
o
Красный полная
корреляция (значение
равно 1),
Оранжевый – значение
стремится к 1,
Желтый – значение
корреляции факторов
0,5,
Зеленый – наиболее
благоприятное
сочетание факторов
37

38.

Основные показатели ценообразующих факторов отобранных для
построения статистической модели в ПК «Массовая оценка»
Наименование
ценообразующего
фактора
Показатели
Коэффициен Коэффициент
т корреляции
значимости
Численность
населения в
населенном пункте
0,38
0,59
Состояние здания
0,16
0,25
Код материала стен
0,3
0,47
0,5
0,76
0,65
1
Расстояние до моря,
лыжных трасс
Расстояние объекта до
центра населенного
пункта
Репрезентатив
-ность
Статистическая
значимость
Репрезентатив
ен
Значимый
Нужна
информация
Репрезентатив
ен
Репрезентатив
ен
Репрезентатив
ен
Значимый
Значимый
Значимый
Значимый
38

39.

Ценовой
дифференциал
(PRD)
экспонен Соответс
циальная твует
Средняя
относительная
погрешность
оценки
мультипл
Соответс
икативна
твует
я
Контрол
ьная
Обучаю
щая
Контрол
ьная
Обучаю
щая
Контрол
ьная
Обучаю
щая
Среднеквадратична
я ошибка оценки
(SEE)
Соответс
линейная
твует
Выборка
Отношение суммы
невязок к средней
стоимости, %
Вывод
Коэффициент
дисперсии (COD)
Модель
Коэффициент
детерминации
Анализ качества статистически значимых моделей оценочной группы
города «Морское побережье» в ПК «Массовая оценка»
0,78
6,88
125,98
8,12
6,86
1,01
0,81
6,25
-0,00000000007
7,64
6,28
1,01
0,78
6,7
180,7
8,21
6,69
1,01
0,81
6,22
44,88
7,75
6,24
1,01
0,73
7,37
193,72
8,99
7,35
1,01
0,77
6,88
54,3
8,5
6,85
1,01
39

40.

Мультипликативная модель для расчета кадастровой стоимости
объектов недвижимости кадастровой стоимости ОКС оценочной
группы города «Морское побережье» в ПК «Массовая оценка»
40

41. Юридический факультет

Землеустроительный
Юридический
факультет
факультет
41