Похожие презентации:
Скрещивающиеся прямые
1.
2.
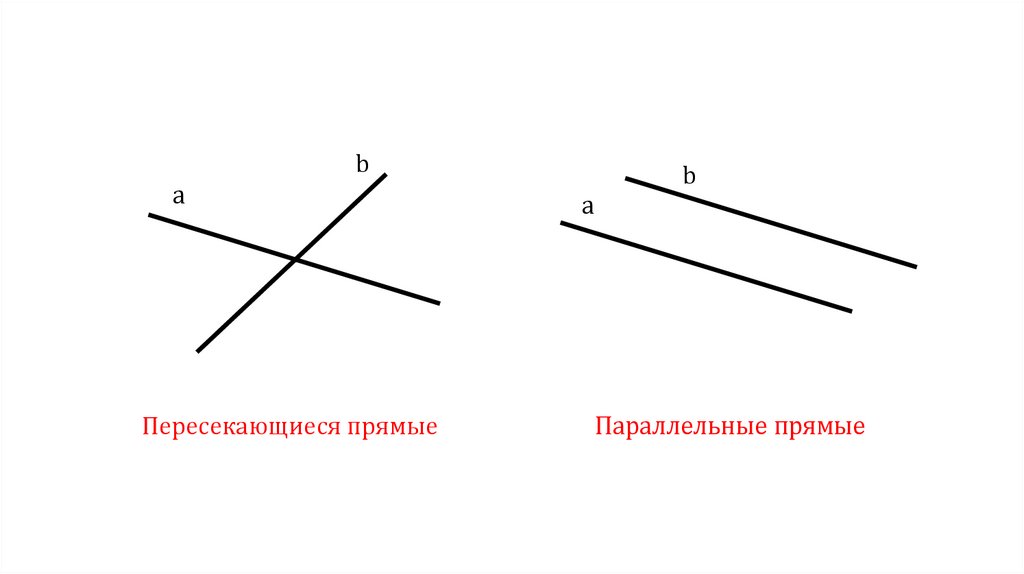
bа
Пересекающиеся прямые
b
а
Параллельные прямые
3.
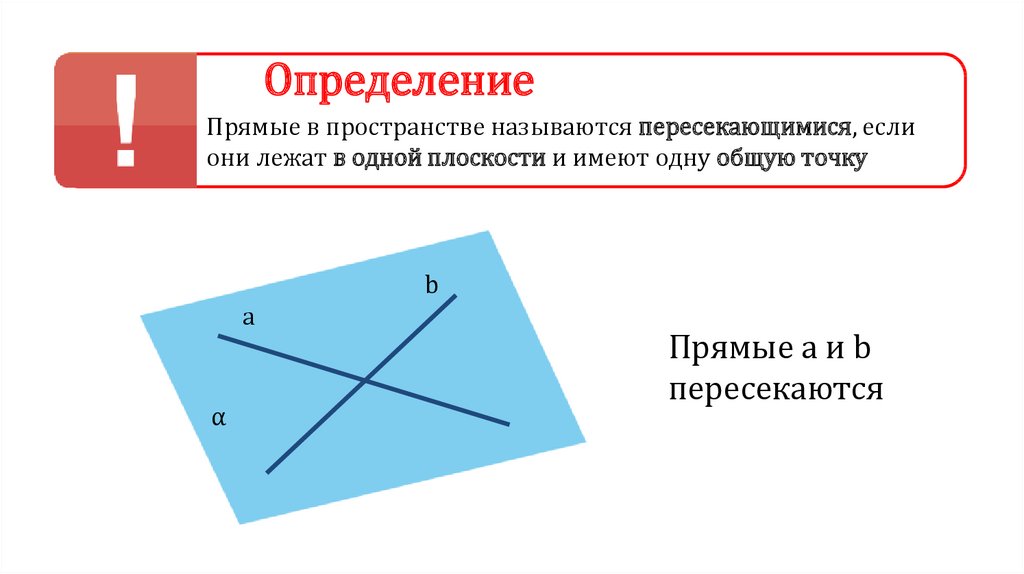
ОпределениеПрямые в пространстве называются пересекающимися, если
они лежат в одной плоскости и имеют одну общую точку
b
а
α
Прямые а и b
пересекаются
4.
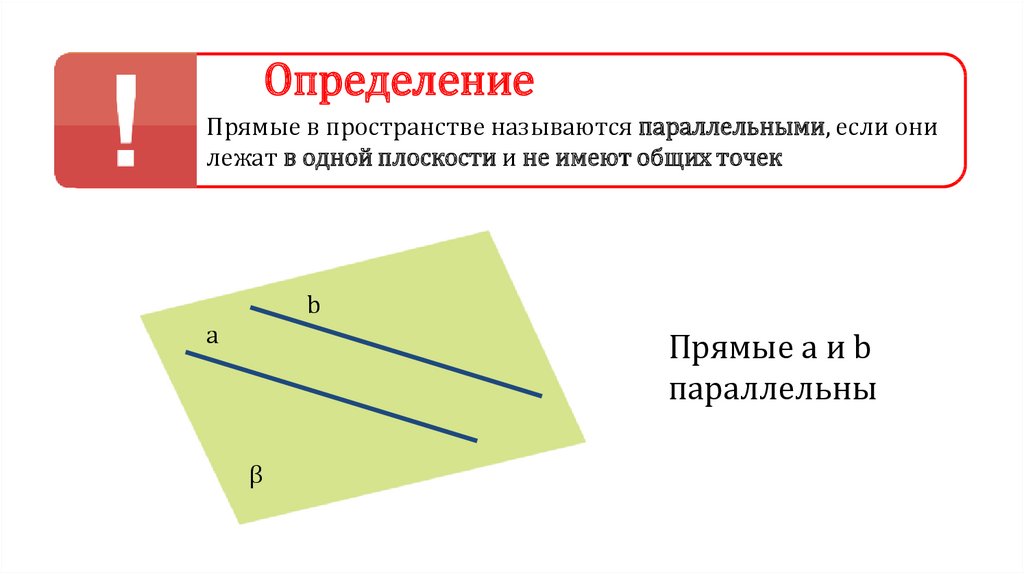
ОпределениеПрямые в пространстве называются параллельными, если они
лежат в одной плоскости и не имеют общих точек
b
а
Прямые a и b
параллельны
β
5.
6.
C1AB и A1D1 лежат в
разных плоскостях
D1
B1
A1
C
D
B
A
7.
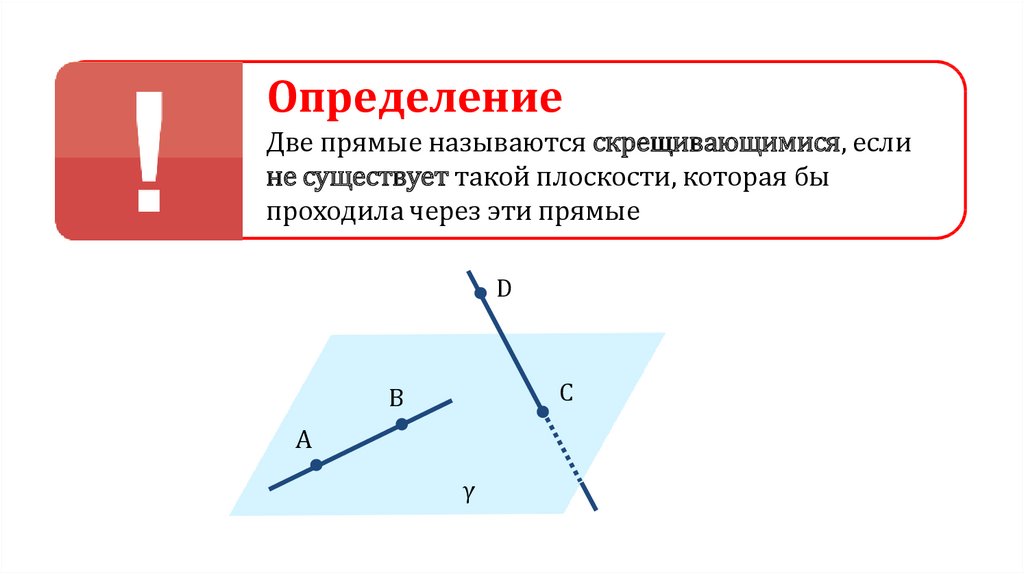
ОпределениеДве прямые называются скрещивающимися, если
не существует такой плоскости, которая бы
проходила через эти прямые
D
C
B
A
γ
8.
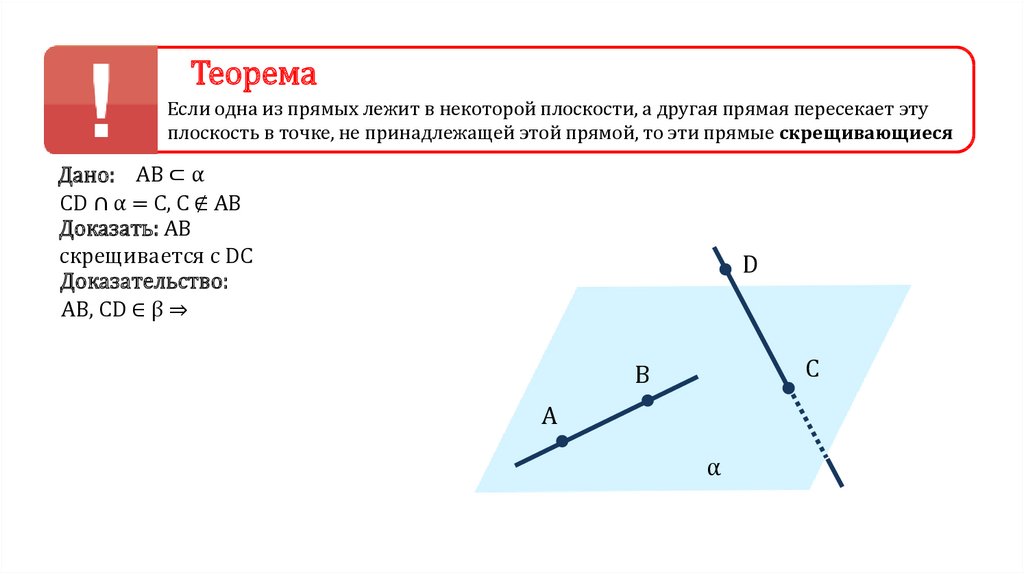
ТеоремаЕсли одна из прямых лежит в некоторой
плоскости, а другая прямая пересекает эту
плоскость в точке, не принадлежащей этой
прямой, то эти прямые скрещивающиеся
9.
ТеоремаЕсли одна из прямых лежит в некоторой плоскости, а другая прямая пересекает эту
плоскость в точке, не принадлежащей этой прямой, то эти прямые скрещивающиеся
Дано: AB ⊂ α
CD ∩ α = C, C ∉ AB
Доказать: AB
скрещивается с DC
Доказательство:
AB, CD ∈ β ⇒
D
C
B
A
α
10.
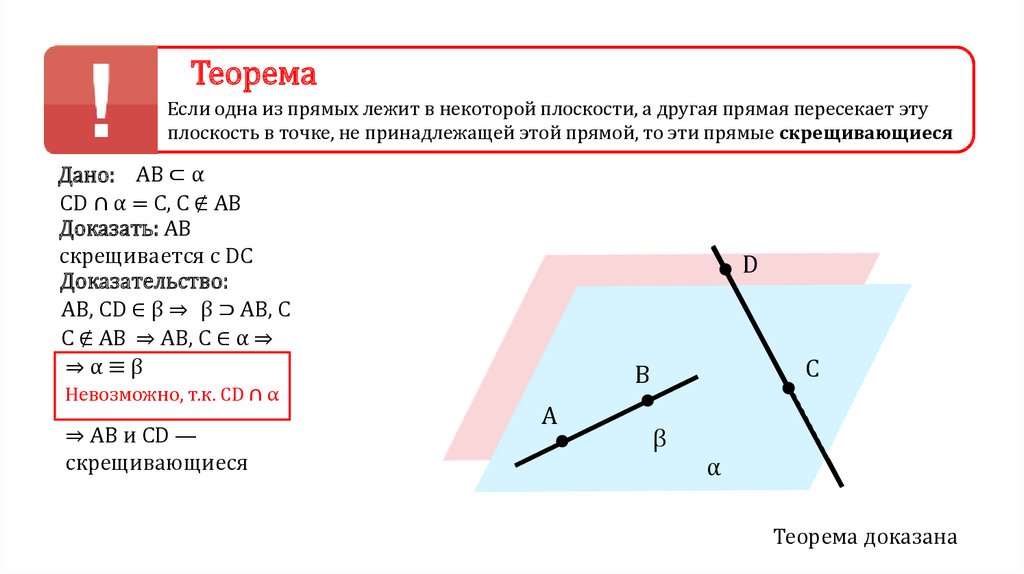
ТеоремаЕсли одна из прямых лежит в некоторой плоскости, а другая прямая пересекает эту
плоскость в точке, не принадлежащей этой прямой, то эти прямые скрещивающиеся
Дано: AB ⊂ α
CD ∩ α = C, C ∉ AB
Доказать: AB
скрещивается с DC
Доказательство:
AB, CD ∈ β ⇒ β ⊃ AB, C
C ∉ AB ⇒ AB, C ∈ α ⇒
⇒α≡β
Невозможно, т.к. CD ∩ α
⇒ AB и CD —
скрещивающиеся
D
C
B
A
β
α
Теорема доказана
11.
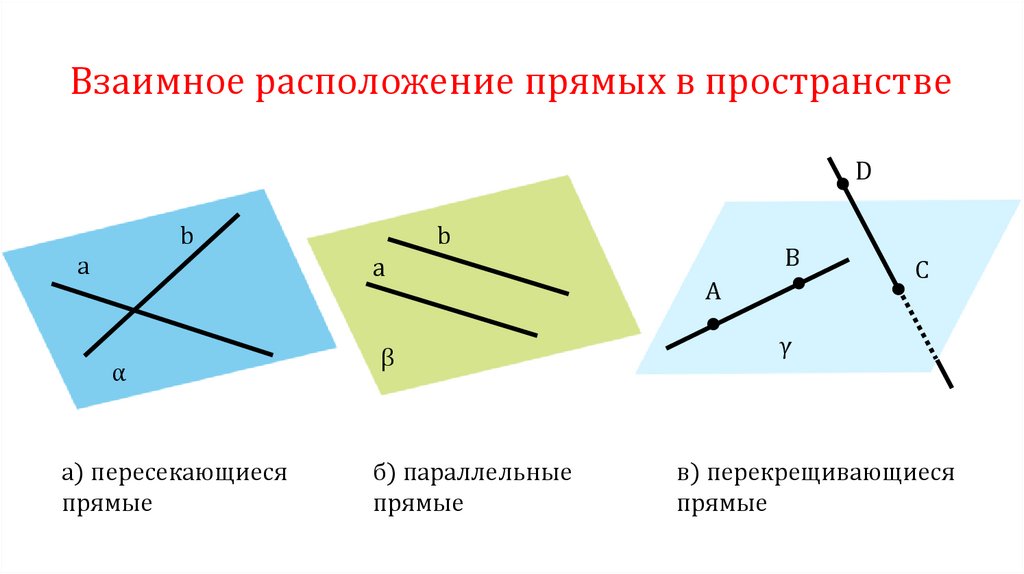
Взаимное расположение прямых в пространствеD
b
а
b
а
α
а) пересекающиеся
прямые
β
б) параллельные
прямые
B
A
C
γ
в) перекрещивающиеся
прямые
12.
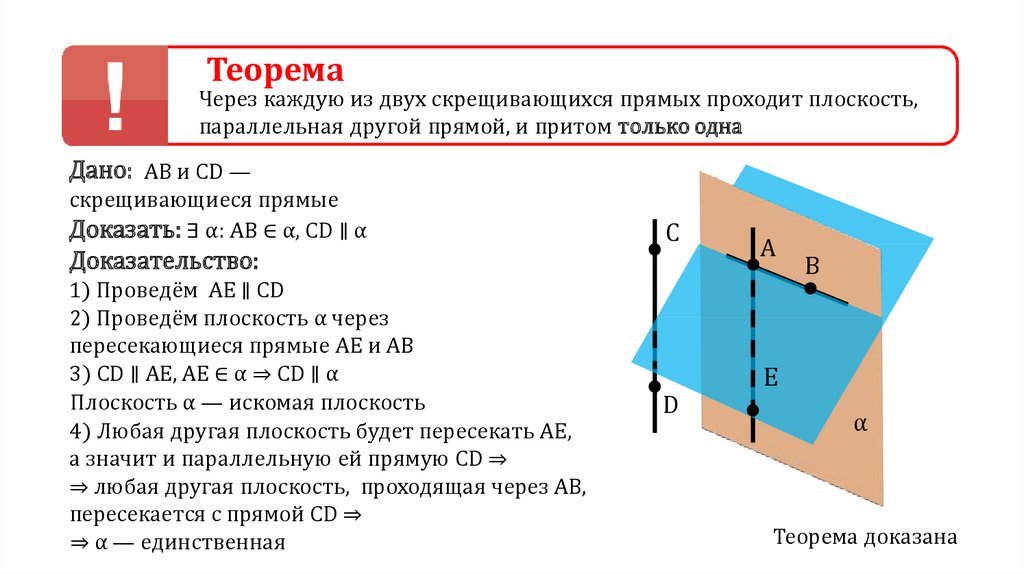
ТеоремаЧерез каждую из двух скрещивающихся
прямых проходит плоскость,
параллельная другой прямой, и притом
только одна
13.
ТеоремаЧерез каждую из двух скрещивающихся прямых проходит плоскость,
параллельная другой прямой, и притом только одна
Дано: АВ и CD —
скрещивающиеся прямые
Доказать: ∃ α: AB ∈ α, CD ∥ α
C
Доказательство:
1) Проведём AE ∥ CD
2) Проведём плоскость α через
пересекающиеся прямые AE и АВ
3) CD ∥ AE, AE ∈ α ⇒ CD ∥ α
Плоскость α — искомая плоскость
4) Любая другая плоскость будет пересекать AE,
а значит и параллельную ей прямую CD ⇒
⇒ любая другая плоскость, проходящая через AB,
пересекается с прямой CD ⇒
⇒ α — единственная
A
B
E
D
α
Теорема доказана
14.
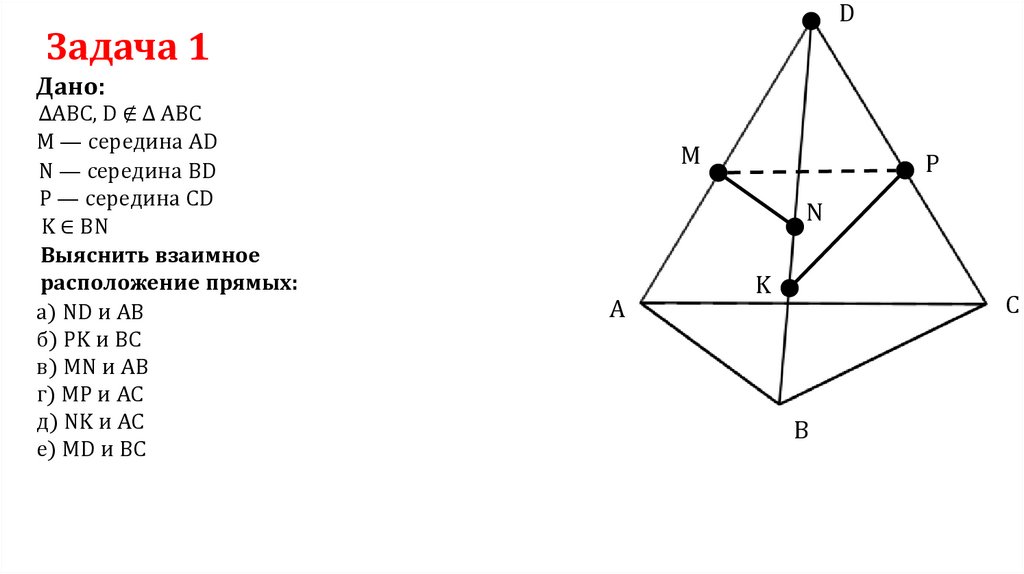
DЗадача 1
Дано:
ΔABC, D ∉ Δ ABC
M — середина AD
N — середина BD
P — середина CD
K ∈ BN
Выяснить взаимное
расположение прямых:
а) ND и AB
б) PK и BC
в) MN и AB
г) MP и AC
д) NK и AC
e) MD и BC
M
P
N
A
K
C
B
15.
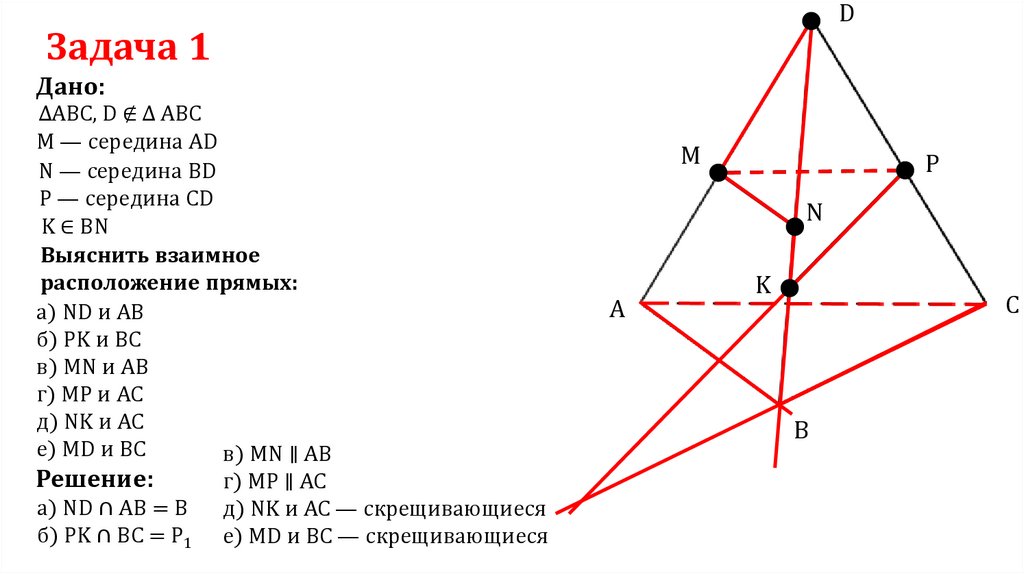
DЗадача 1
Дано:
ΔABC, D ∉ Δ ABC
M — середина AD
N — середина BD
P — середина CD
K ∈ BN
Выяснить взаимное
расположение прямых:
а) ND и AB
б) PK и BC
в) MN и AB
г) MP и AC
д) NK и AC
e) MD и BC
в) MN ∥ AB
Решение:
г) MP ∥ AC
а) ND ∩ AB = B
д) NK и AC — скрещивающиеся
б) PK ∩ BC = P1 е) MD и BC — скрещивающиеся
M
P
N
A
K
C
B
16.
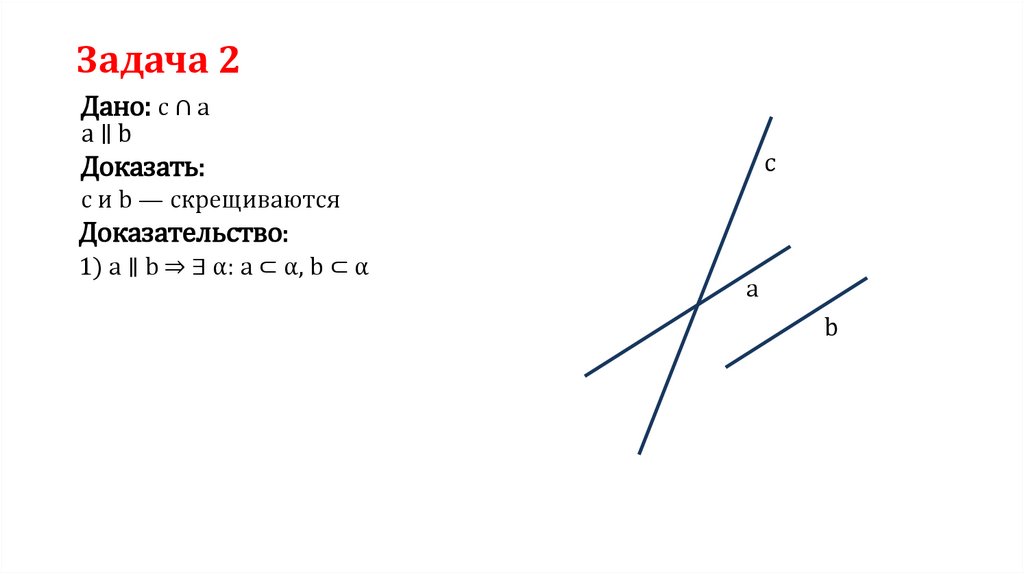
Задача 2Дано: c ∩ a
a∥b
c
Доказать:
с и b — скрещиваются
Доказательство:
1) a ∥ b ⇒ ∃ α: a ⊂ α, b ⊂ α
a
b
17.
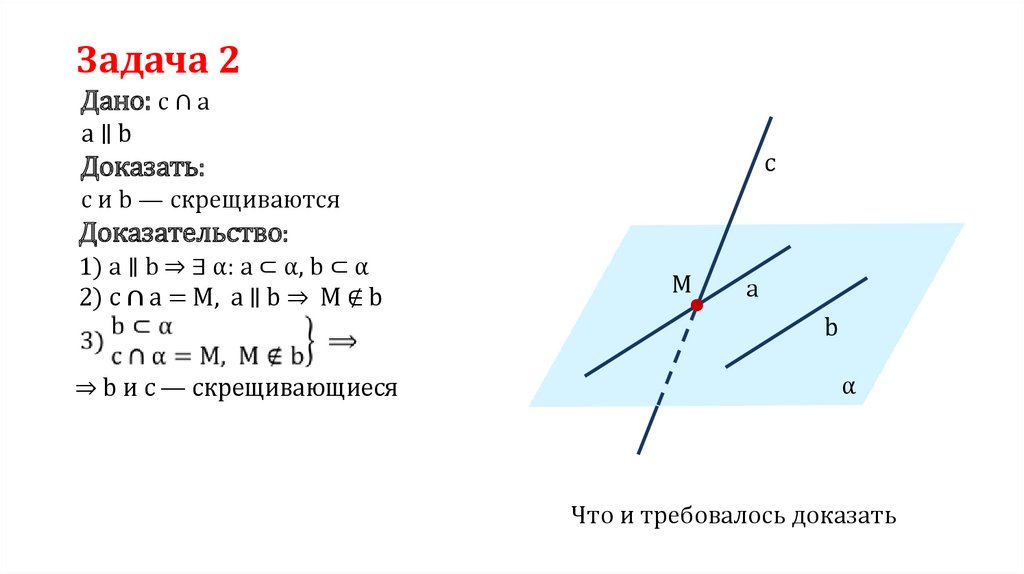
Задача 2Дано: c ∩ a
a∥b
c
Доказать:
с и b — скрещиваются
Доказательство:
1) a ∥ b ⇒ ∃ α: a ⊂ α, b ⊂ α
2) c ∩ a = M, a ∥ b ⇒ M ∉ b
M
a
b
⇒ b и c — скрещивающиеся
α
Что и требовалось доказать





 Математика
Математика








