Похожие презентации:
Взаимное расположение прямых в пространстве. Скрещивающиеся прямые
1.
Стереометрия2.
Вопросы для повторенияКаково взаимное расположение прямой и
плоскости в пространстве?
Сформулируйте определение параллельности
прямой и плоскости в пространстве
(приведите примеры).
Сформулируйте признак параллельности
прямой и плоскости в пространстве (Т5).
Сформулируйте следствия из (Т5).
3.
Взаимное расположение прямых в пространствеУгол между двумя прямыми
4.
ввести определение скрещивающихсяпрямых;
изучить взаимное расположение
прямых в пространстве;
сформулировать признак
скрещивающихся прямых и теорему о
них (Т6, Т7);
применить полученные сведения при
решении задач.
5.
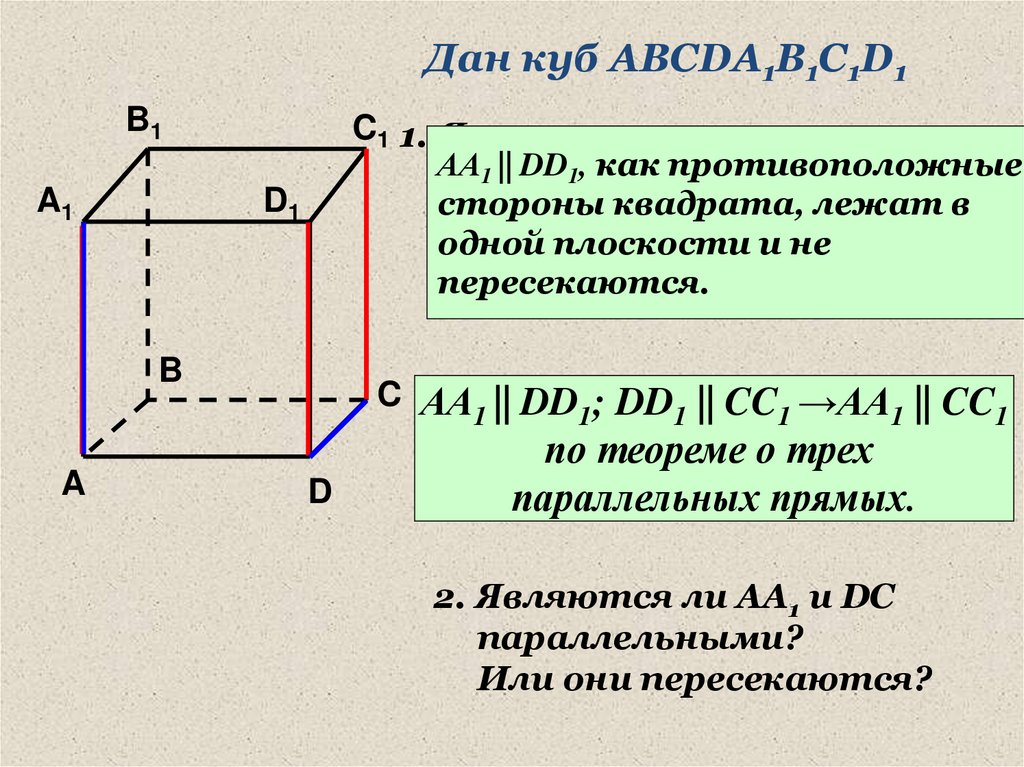
Дан куб АВСDA1B1C1D1B1
A1
C1 1. Являются ли
АА
1 || DD1, как противоположные
параллельными
стороныАА
квадрата,
лежат
в?
прямые
и
DD
;
АА
и
СС
1
1
1
1
одной
плоскости
и
не
Почему?
пересекаются.
D1
B
A
C АА || DD ; DD || CC →AA || CC
1
1
1
1
1
1
D
по теореме о трех
параллельных прямых.
2. Являются ли АА1 и DC
параллельными?
Или они пересекаются?
6.
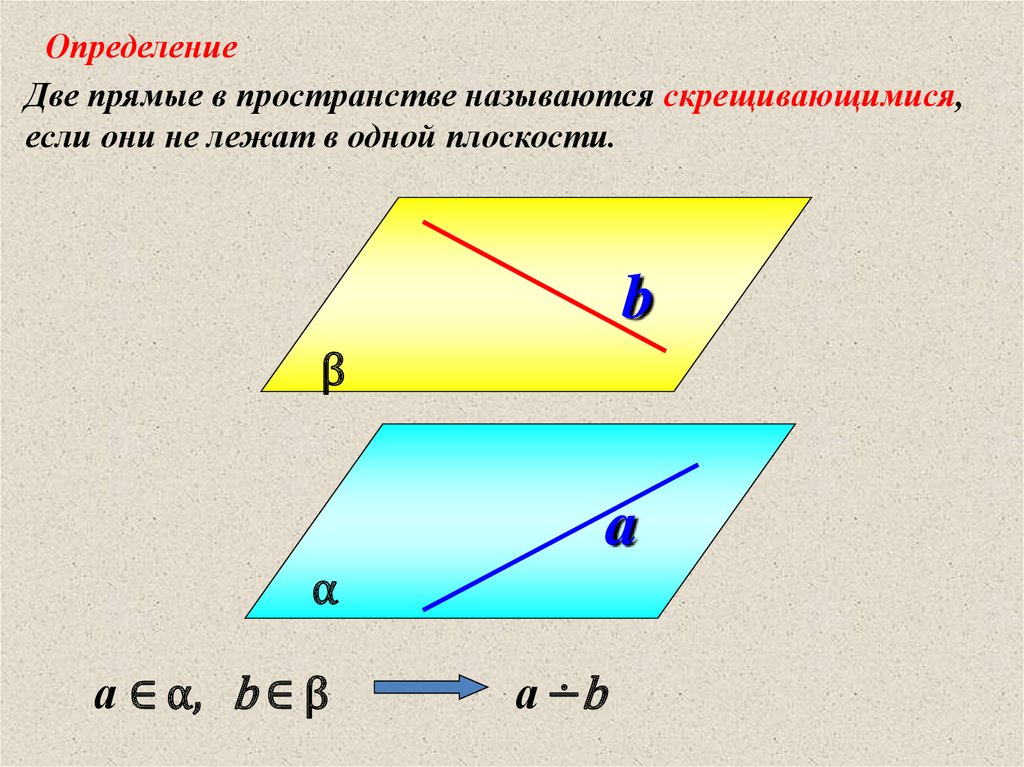
ОпределениеДве прямые в пространстве называются скрещивающимися,
если они не лежат в одной плоскости.
b
β
a
α
а ∈ α, b ∈ β
а ∸b
7.
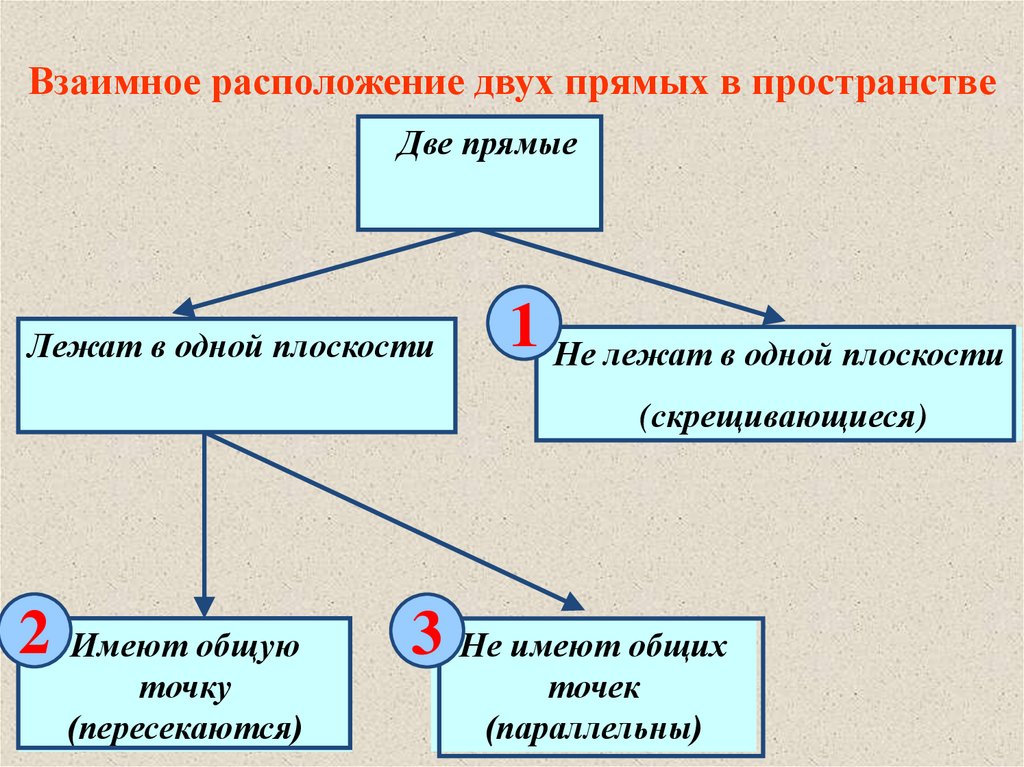
Взаимное расположение двух прямых в пространствеДве прямые
Лежат в одной плоскости
1 Не лежат в одной плоскости
(скрещивающиеся)
2
Имеют общую
точку
(пересекаются)
3 Не имеют общих
точек
(параллельны)
8.
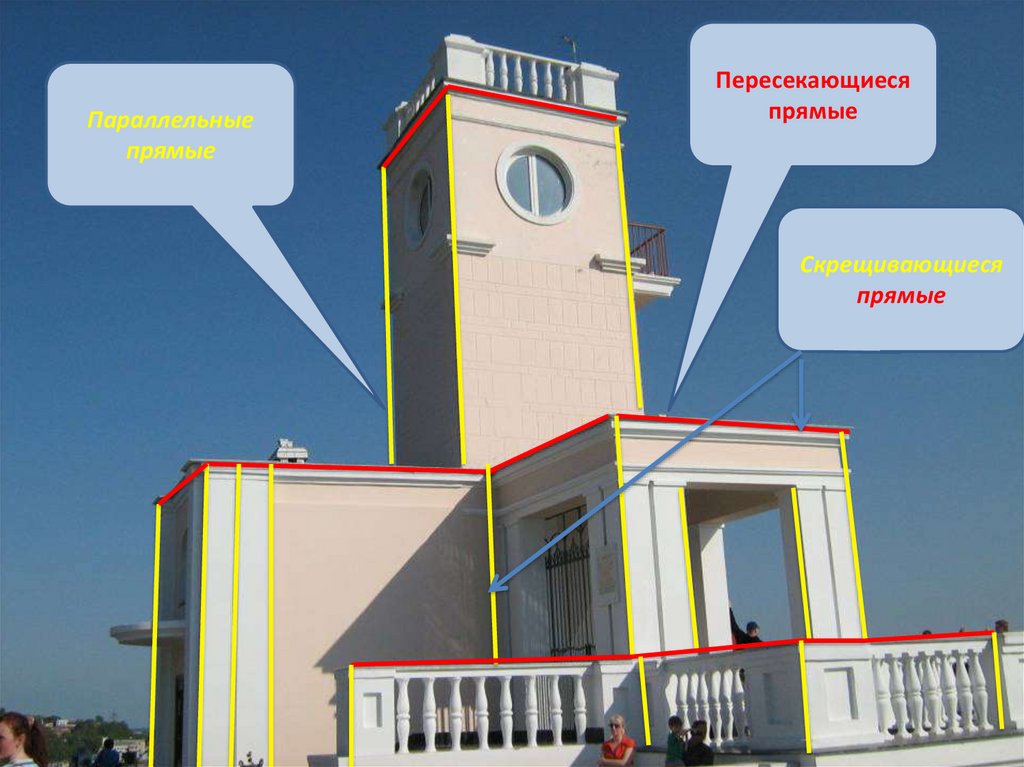
Параллельныепрямые
Пересекающиеся
прямые
Скрещивающиеся
прямые
9.
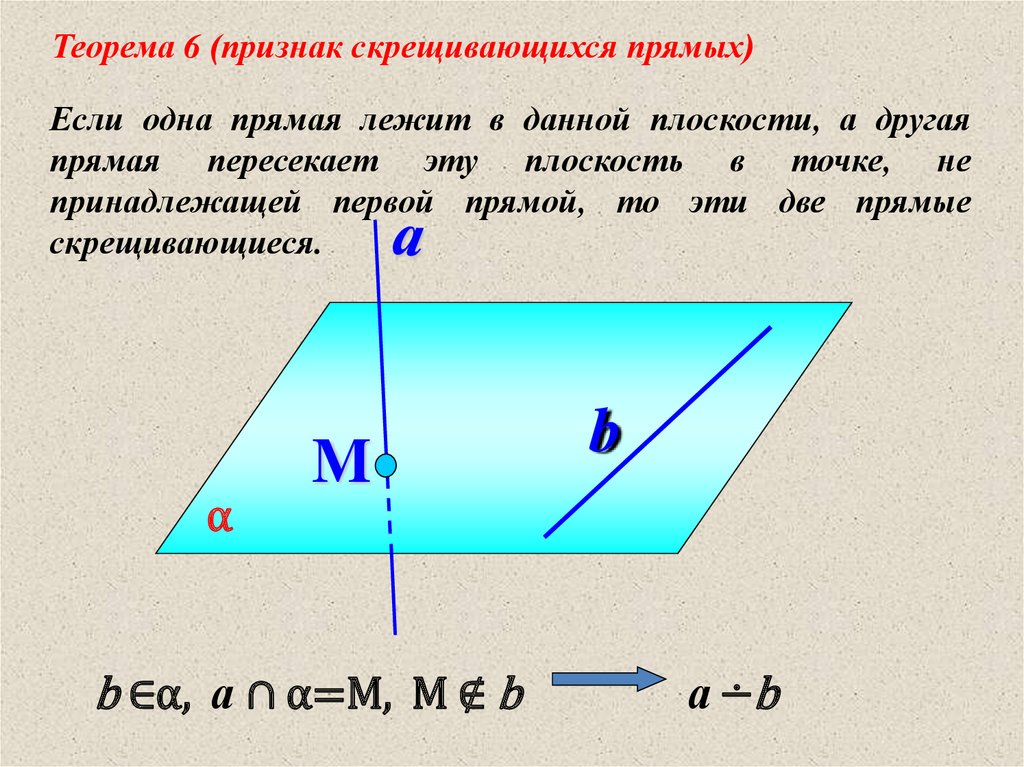
Теорема 6 (признак скрещивающихся прямых)Если одна прямая лежит в данной плоскости, а другая
прямая пересекает эту плоскость в точке, не
принадлежащей первой прямой, то эти две прямые
скрещивающиеся.
b
α
M
b ∈α, а ∩ α=M, M ∉ b
b
а ∸b
10.
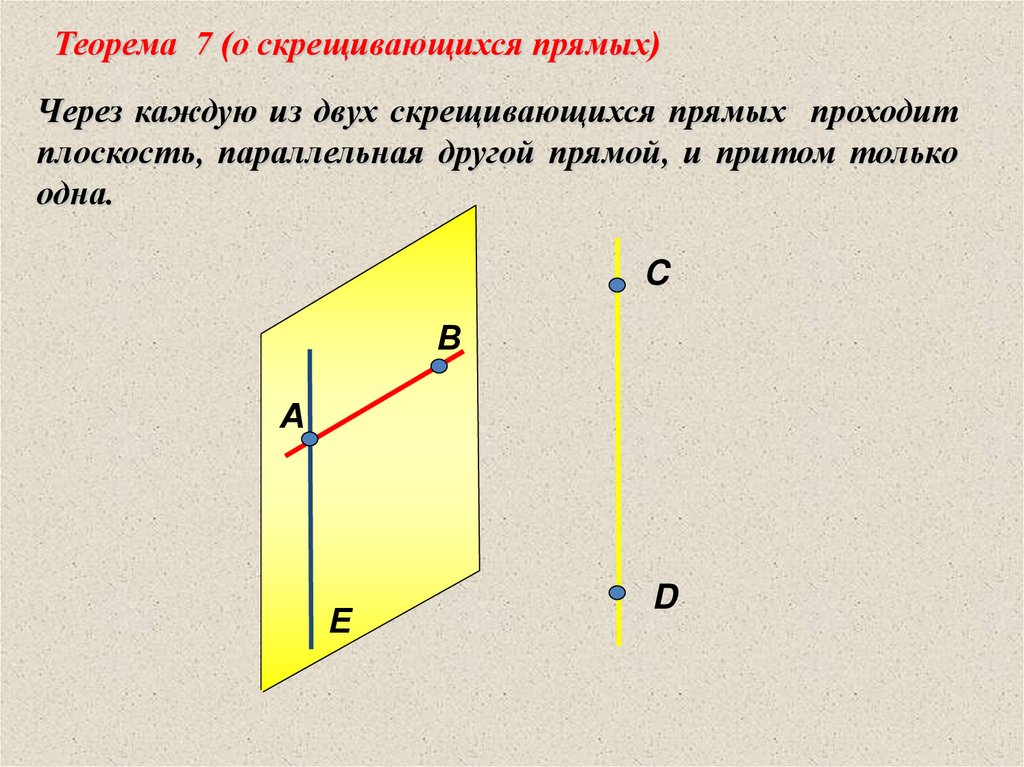
Теорема 7 (о скрещивающихся прямых)Через каждую из двух скрещивающихся прямых проходит
плоскость, параллельная другой прямой, и притом только
одна.
C
В
А
Е
D
11.
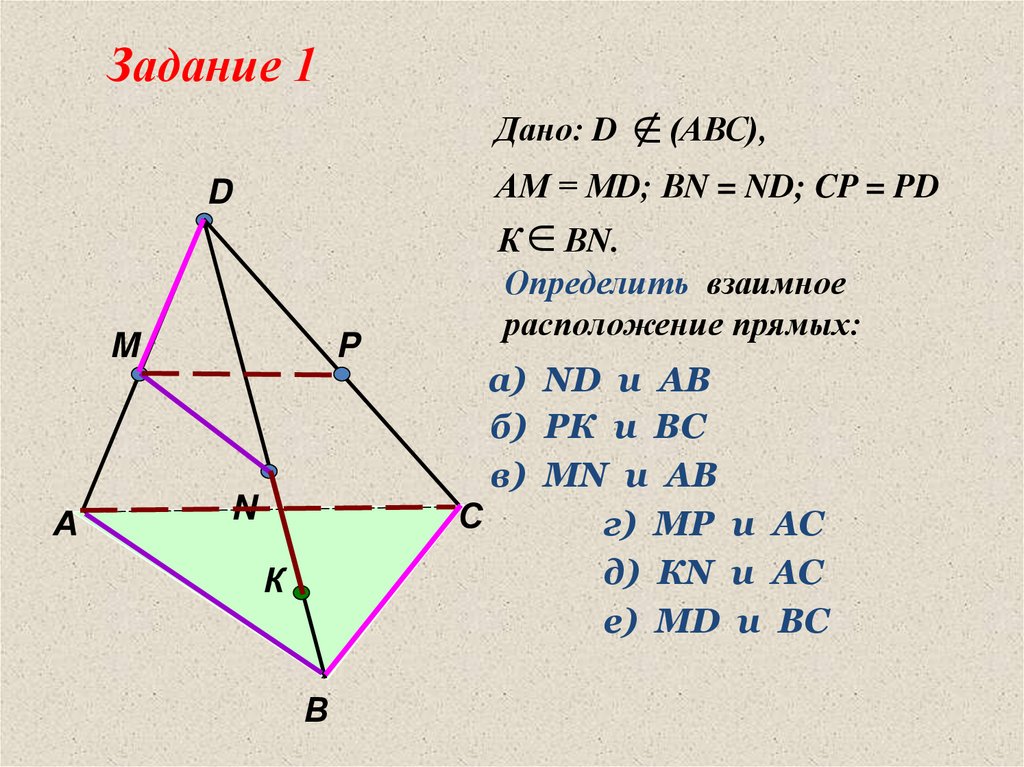
Задание 1Дано: D
АМ = МD; ВN = ND; CP = PD
D
M
А
(АВС),
P
N
К
В
К ВN.
Определить взаимное
расположение прямых:
а) ND и AB
б) РК и ВС
в) МN и AB
С
г) МР и AС
д) КN и AС
е) МD и BС
12.
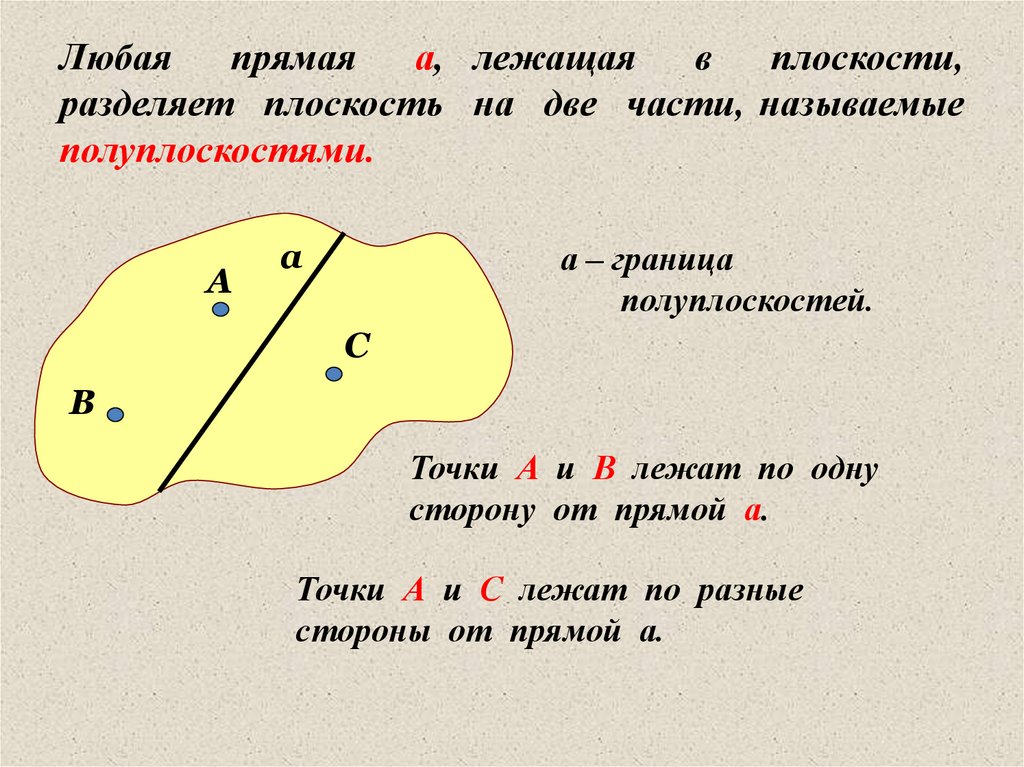
Любаяпрямая
а, лежащая
в
плоскости,
разделяет плоскость на две части, называемые
полуплоскостями.
А
а
а – граница
полуплоскостей.
С
В
Точки А и В лежат по одну
сторону от прямой а.
Точки А и С лежат по разные
стороны от прямой а.
13.
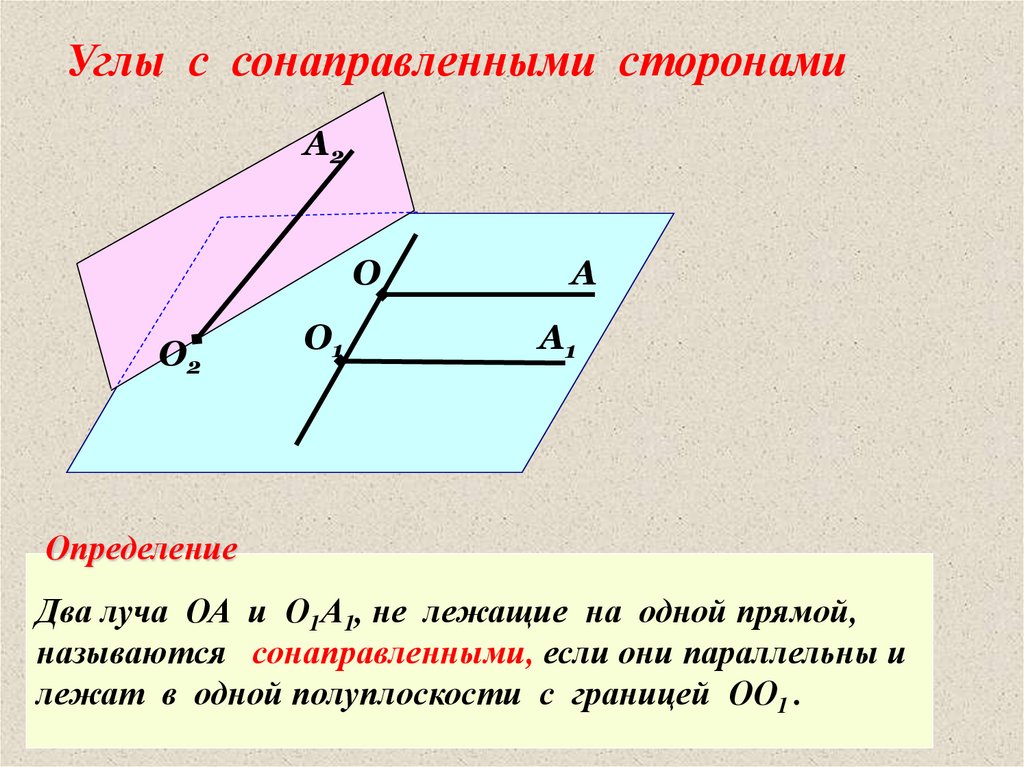
Углы с сонаправленными сторонамиА2
О
О2
О1
А
А1
Определение
Два луча ОА и О1А1, не лежащие на одной прямой,
называются сонаправленными, если они параллельны и
лежат в одной полуплоскости с границей ОО1 .
14.
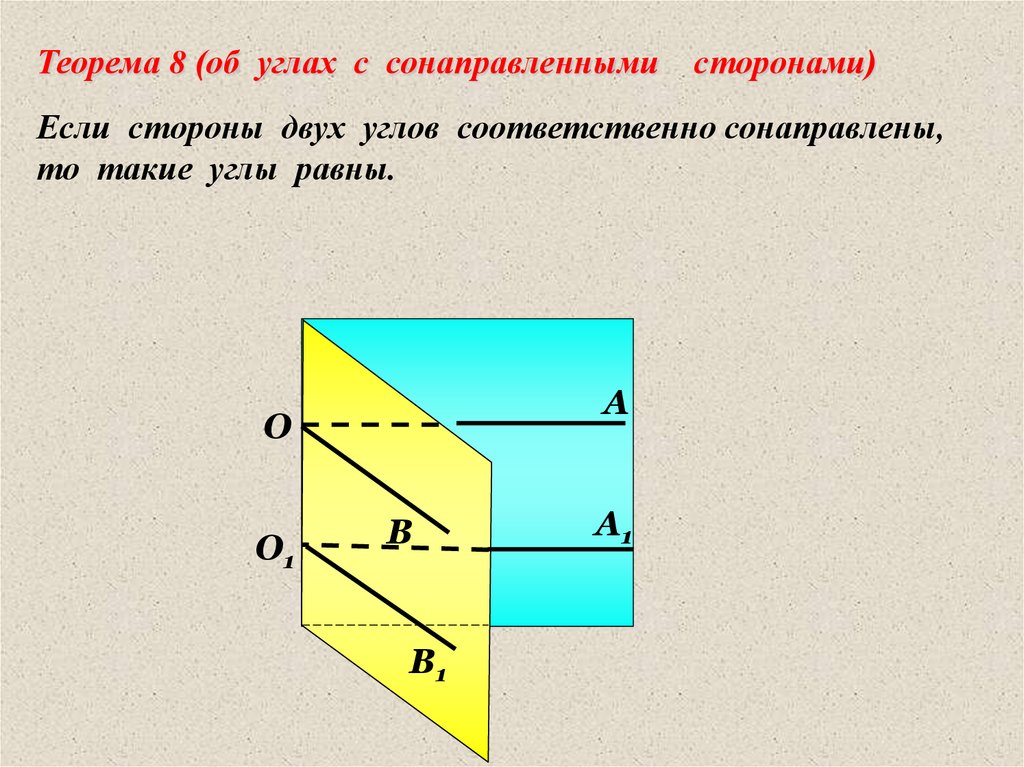
Теорема 8 (об углах с сонаправленнымисторонами)
Если стороны двух углов соответственно сонаправлены,
то такие углы равны.
А
О
О1
В
В1
А1
15.
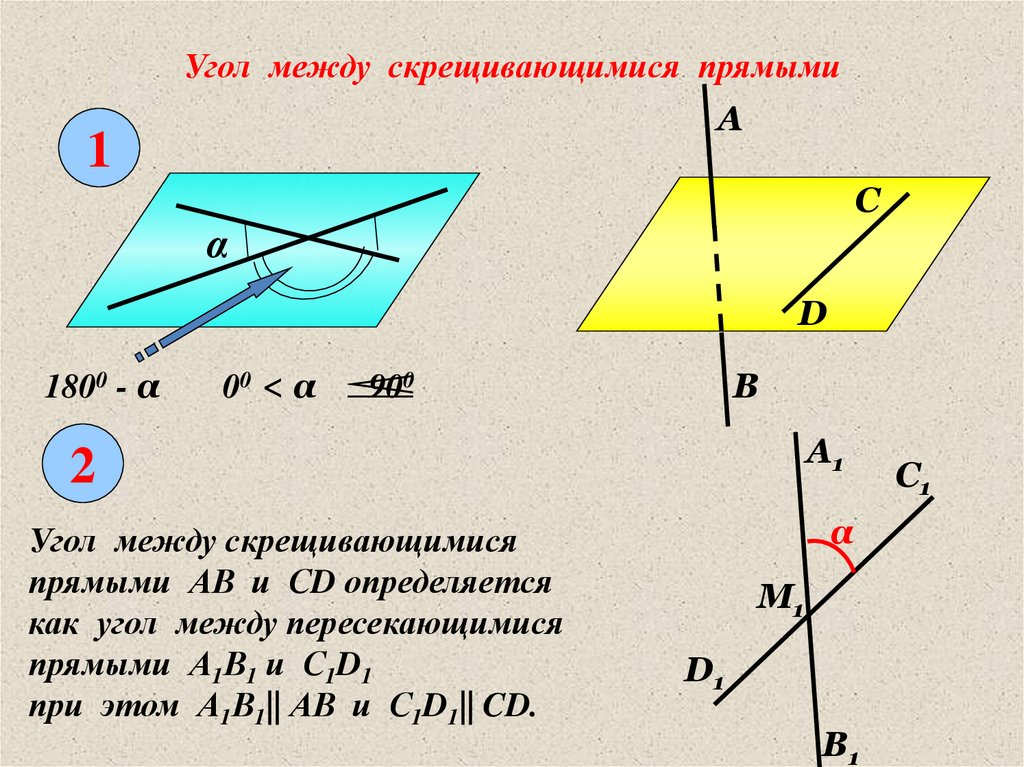
Угол между скрещивающимися прямымиА
1
С
α
D
1800 - α
00 < α
900
В
А1
2
Угол между скрещивающимися
прямыми АВ и СD определяется
как угол между пересекающимися
прямыми А1В1 и С1D1
при этом А1В1|| АВ и С1D1|| CD.
α
М1
D1
В1
С1
16.
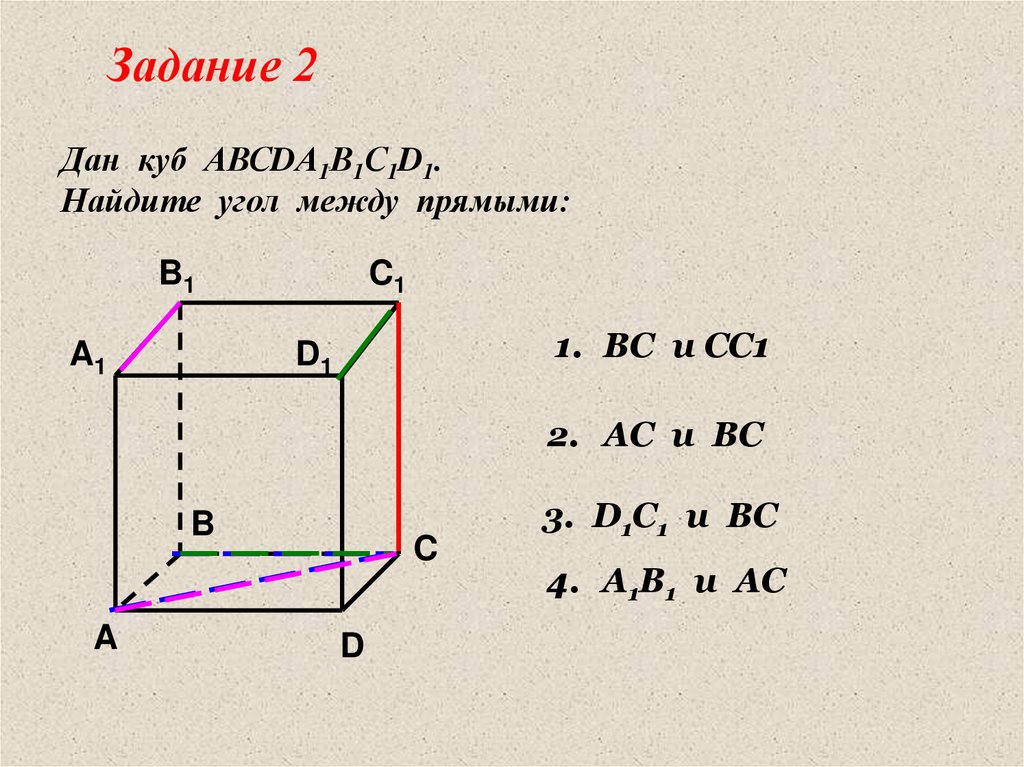
Задание 2Дан куб АВСDА1В1С1D1.
Найдите угол между прямыми:
B1
A1
C1
1. ВС и СС1
D1
2. АС и ВС
B
A
C
D
3. D1С1 и ВС
4. А1В1 и АС
17.
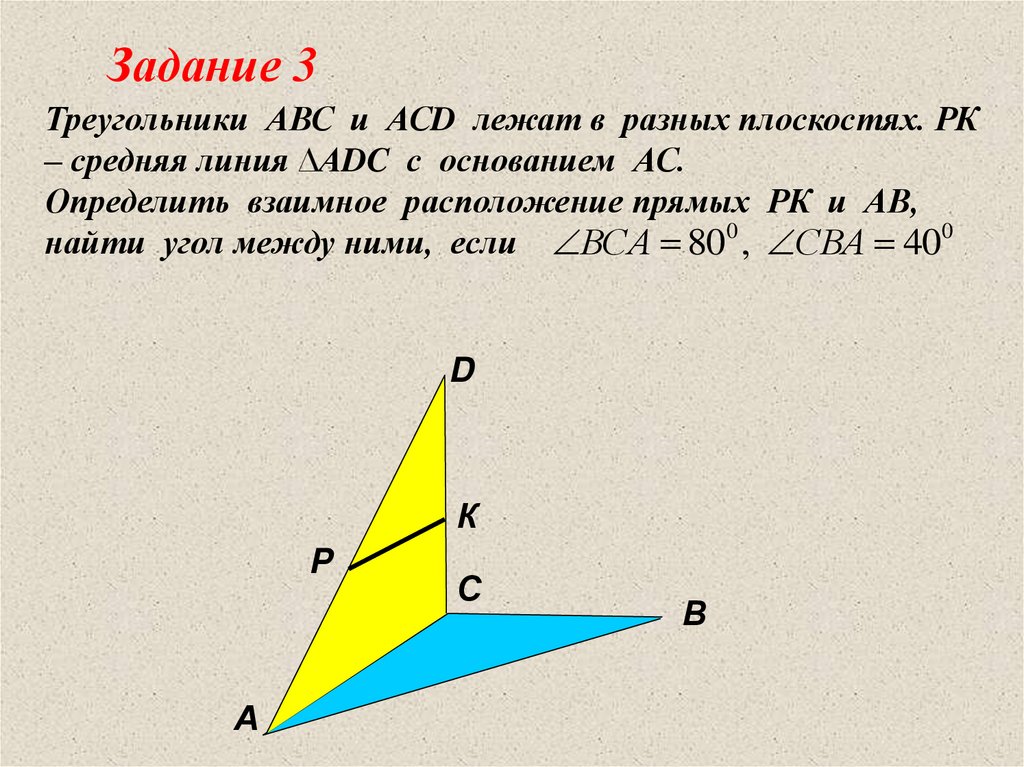
Задание 3Треугольники АВС и АСD лежат в разных плоскостях. РК
– средняя линия ∆АDC с основанием АС.
Определить взаимное расположение прямых РК и АВ,
найти угол между ними, если ВСА 800 , СВА 400
D
К
P
А
С
В
18.
Задача 1.Задача 2.
Задача 3.
18
19.
- Дайте определение скрещивающихсяпрямых.
- Расскажите о взаимном расположении
прямых в пространстве.
- Сформулируйте признак скрещивающихся
прямых и теорему о них (Т6, Т7).
- Как определить угол между
скрещивающимися прямыми?
19






 Математика
Математика








