Похожие презентации:
Уравнение. Дифференциальные уравнения первого порядка
1.
Уравнение видаF ( x, y, y ) 0
называется ДУ первого порядка.
Где х – независимая переменная;
у– неизвестная функция;
у‘ – ее производная.
2.
Если из уравнения можно выразить производнуюнеизвестной функции, то оно примет вид:
y f ( x, y )
2
Это уравнение называется ДУ первого порядка,
Например:
2
2
2
(y ) x y
tgy xy 0
2
2
2
y x y
y arctg ( xy )
2
3.
Решением ДУ первого порядка называетсяфункция у=φ(х), определенная на
некотором интервале (a,b), которая
при подстановке ее в уравнение
обращает его в тождество.
4.
Пусть дано ДУ (2). Если функция f(x,y) и еечастная производная f‘y(x,y) непрерывны
в некоторой области D плоскости ХОУ,
то в некоторой окрестности любой
внутренней точки (х0,у0) этой области
существует единственное решение этого
уравнения, удовлетворяющего условию
х=х0, у=у0.
5.
заключается в том, что график решения ДУ естьинтегральная кривая. В области D содержится
бесконечно много интегральных кривых. Теорема
гарантирует, что при соблюдении определенных
условий через каждую внутреннюю точку области
проходит только одна интегральная кривая.
Условия,
задающие
значения
функции
в
фиксированной точке называются начальными
условиями (условиями Коши):
y x x y0
0
3
6.
Задача решения уравнения (2), удовлетворяющегоусловию (3) называется задачей Коши.
(из множества интегральных кривых выделяется
та, которая проходит через заданную точку).
В некоторых случаях, если условия теоремы Коши
не выполнены, через точку вообще не проходит
интегральная кривая, или их проходит несколько.
Такие точки называются
7.
уравнения (2) называется функцияy ( x, C )
удовлетворяющая
этому
произвольном значении С.
уравнению
при
уравнения (2) называется функция
y ( x, C0 )
полученная при определенном значении С=С0.
8.
Рассмотрим уравнениеy 2 x
Правая часть уравнения удовлетворяет всем
условиям теоремы Коши во всех точках плоскости
ХОУ:
Функции f(x,y)=2x и f‘y=0
непрерывны на всей плоскости.
Общее решение уравнения:
y x C
2
определены
и
9.
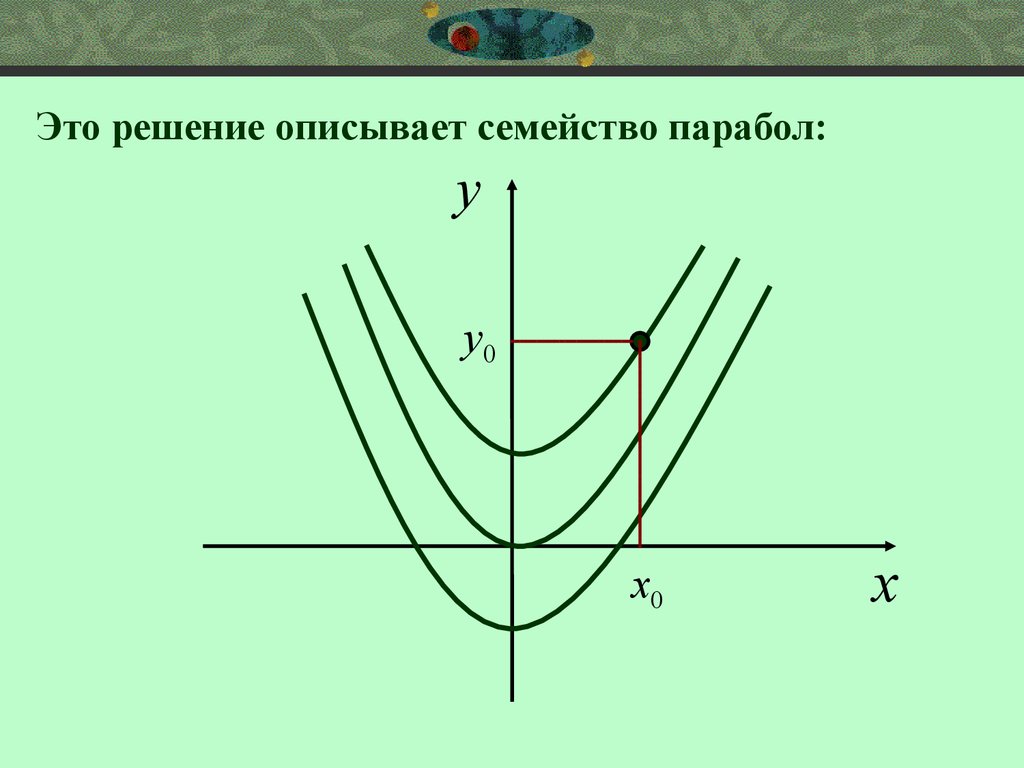
Это решение описывает семейство парабол:y
y0
x0
x
10.
Для нахождения частного решения зададимначальные условия (3) и подставим их в общее
решение:
C y0 x0
2
y x y0 x
2
2
0
Это частное решение выделяет из семейства
парабол одну, проходящую через точку (х0,у0).









 Математика
Математика








