Похожие презентации:
Обыкновенные дифференциальные уравнения первого порядка
1. Обыкновенные дифференциальные уравнения первого порядка
{ задача Коши - геометрическая интерпретация дифференциального уравнения первого порядка - уравнения сразделенными и разделяющимися переменными - однородные дифференциальные уравнения - линейные
дифференциальные уравнения - метод Бернулли - метод Лагранжа - уравнение Бернулли - уравнения, не
разрешенные относительно производной – пример }
2.
Задача отыскания решения дифференциального уравненияdy
f ( x ,y )
dx
удовлетворяющего заданным начальным условиям y(x0 ) = y0 , называется
задачей Коши.
Теорема
Если функция f - правая часть
дифференциального уравнения
dy/dx = f(x,y) непрерывна в некоторой
замкнутой области D плоскости xoy и имеет в
этой области ограниченную частную
производную дf(x,y)/дy, то каждой внутренней
точке области D соответствует, и притом
единственное, решение, удовлетворяющее
Огюстен Луи Коши
(Augustin Louis Cauchy)
заданным начальным условиям.
1789 – 1857
3.
Геометрически это означает, что через каждую точку M0 (x0,y0) области Dпроходит одна и только одна интегральная кривая рассматриваемого
уравнения.
Данная теорема называется теоремой существования и единственности
решения дифференциального уравнения
y
y ( x )
M0 (x0,y0)
dy
f ( x ,y )
dx
D
x
o
y ( x )
y ( x0 ) y0
y ( x0 ) ( x0 )
d ( x )
f ( x , ( x ))
dx
4.
@Решить дифференциальное уравнение первого порядка, при
заданных начальных условиях
dy
xy y ( 0 ) 1
dx
y
Решение
dy
dy
xy
xdx
dx
y
2
dy
y
x
ln | y |
ln C y
2
y ( 0 ) 1 Ce 0 1
xdx
x2
Ce 2
y
M(0,1)
x2
e2
o
x
5.
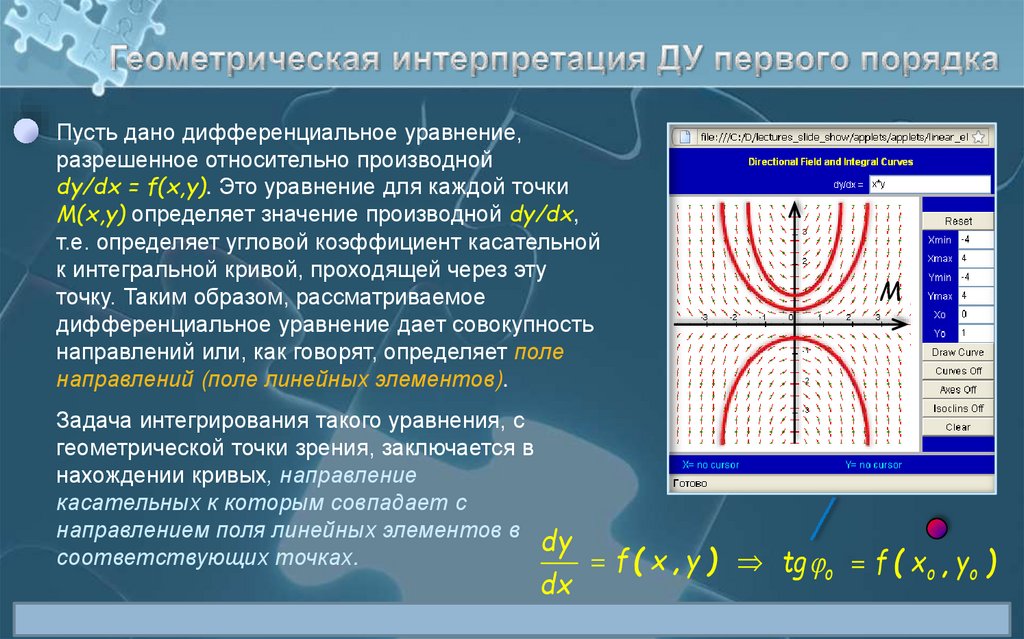
Пусть дано дифференциальное уравнение,разрешенное относительно производной
dy/dx = f(x,y). Это уравнение для каждой точки
M(x,y) определяет значение производной dy/dx,
т.е. определяет угловой коэффициент касательной
к интегральной кривой, проходящей через эту
точку. Таким образом, рассматриваемое
дифференциальное уравнение дает совокупность
направлений или, как говорят, определяет поле
направлений (поле линейных элементов).
Задача интегрирования такого уравнения, с
геометрической точки зрения, заключается в
нахождении кривых, направление
касательных к которым совпадает с
направлением поля линейных элементов в
dy
соответствующих точках.
dx
M
f ( x , y ) tg o f ( x o , y o )
6.
Уравнением с разделенными переменными называется уравнение вида:M ( x ) dx N ( y ) dy 0
Решение: прямое интегрирование -
M ( x ) dx N ( y ) dy
C
Уравнением с разделяющимися переменными называется уравнение вида:
M1 ( x ) N 1 ( y ) dx M2 ( x ) N 2 ( y ) dy 0
Решение: приведение к виду уравнения с разделенными переменными
путем деления обеих его частей на произведение N1 (y) M2 (x)
M1 ( x )
N2 ( y )
dx
M2 ( x )
N1 ( y ) dy C
7.
@Решить дифференциальное уравнение
dy
1 y2
dx
2 xy
Решение
dy
1 y2
2 ydy
dx
2
dx
2 xy
x
1 y
2 ydy
1 y2
dx
x
d(1 y2 )
dx
2
ln
|
1
y
| ln | x | ln C
2
x
1 y
1
2
Cx
x
(
1
y
) C
2
1 y
8.
Уравнение M(x,y) dx + N(x,y) dy = 0 называется однороднымдифференциальным уравнением первого порядка, если функции M(x,y)
и N(x,y) являются однородными функциями одного и того же измерения:
M ( tx ,ty ) t n M ( x , y ), N ( tx ,ty ) t n N ( x , y )
Если уравнение может приведено к виду: dy/dx = F(x,y) = F(v) ,
где v = y/x, то оно называется однородным дифференциальным
уравнением первого порядка.
Решение: для приведения к уравнению с разделяющимися переменными
используется подстановка
v
y
y xv
x
dv
dx
F (v ) v
x
dy
dv
dv
x
v x
v F (v )
dx
dx
dx
dv
dx
dv
F (v ) v x
F ( v ) v ln | x | C
9.
@Решить дифференциальное ( y 2 3 x 2 ) dx 2 xydy 0 , y ( 1 ) 2
уравнение
Частное решение
Решение
y
v
dy xdv vdx
x
x 2 ( v 2 3 )dx 2 x 2v ( xdv vdx ) 0
xy 2 x 3 3
( 2 2 1 2 )1 C
C 3
2 vdv
3 dx
2 vdv
dx
0 2
3
C
( 3v 3 )dx 2v ( xdv ) 0 2
x
x
v 1
v 1
2
ln( v 2 1 ) 3 ln x ln C
Общий интеграл
( y2 x 2 )x C
10.
Уравнение y P ( x ) y Q ( x ) , где P(x) и Q(x) - заданные непрерывныефункции, называется линейным дифференциальным уравнением первого порядка.
Если функция Q(x) = 0, то уравнение называется линейным однородным, в
противном случае - линейным неоднородным.
Метод Бернулли
Якоб Бернулли
(Jacob Bernoulli)
1654 - 1705
Применим подстановку y = u(x) v(x), где u(x) – новая неизвестная
функция, v(x) – произвольная функция, которую подчиним
некоторому условию
y ( uv ) u v u v u v u ( v P ( x ) v ) Q ( x )
dv
P ( x ) dx
v P( x ) v 0
P ( x ) dx v e
v
du P ( x ) dx
e
Q ( x ) u Q ( x ) e P ( x ) dx dx c
dx
y e P ( x ) dx ( Q ( x ) e P ( x ) dx dx c )
11.
Метод Лагранжа решения линейного уравнения– метод вариации произвольной постоянной
y P( x )y Q( x )
Сначала решаем однородное уравнение
y P ( x ) y 0 y Ce P ( x ) dx
Полученное решение подставляем в исходное
неоднородное дифференциальное уравнение, варьируя
(считая переменной) постоянную C .
d ( C ( x ) e P ( x ) dx )
P ( x ) dx
P ( x )C ( x )e
Q( x )
dx
C ( x ) Q( x
Жозеф Луи Лагранж
(Joseph-Louis Lagrange)
1736 - 1813
P ( x ) dx
P ( x ) dx
P ( x ) dx
C 'e
P ( x )C ( x )e
P ( x )C ( x )e
P ( x ) dx
dC
Q( x )
e
Q( x )
dx
P ( x ) dx
)e
dx
~
C
y e P ( x ) dx ( Q ( x ) e P ( x ) dx dx C )
12.
@Решить дифференциальное уравнение
Метод Лагранжа
Решение
dy
2 xy
dy
2 xdx
0
2
2
dx 1 x
y
1 x
y C ( x )( 1 x 2 )
y ( x C )( 1 x 2 )
dy
2 xy
2
1
x
dx 1 x 2
dy
y
2 xdx
1 x2
y C(1 x2 )
~
dC
(1 x2 ) 1 x2 C( x ) x C
dx
y C (1 x2 ) x x3
13.
Уравнением Бернулли называется уравнение вида:y P( x )y Q( x )yn
При n = 0 и n = 1 – уравнение становится линейным (неоднородным или однородным)
1 dy
1
P
(
x
)
Q( x )
n
n 1
y dx
y
1
Уравнение Бернулли приводится к
z
линейному с использованием подстановки y n 1
Уравнение можно представить в виде:
Другой способ решения (Бернулли):
ищем решение в виде U(x)V(x),
на одну из функций накладываем
условие:
dv
P ( x )v 0
dx
d y 1 n
dz
1 n dy
dx
dx
y n dx
dz
( 1 n ) P ( x ) z ( 1 n )Q ( x )
dx
14.
@Решить дифференциальное уравнение
x
dv
x
v 0
dx
1
)
2
u
u
x
2 ln x
dx
x
x
d(u
du
u2
ln x
x 2 dx
dy
y y 2 ln x
dx
Решение
Метод Бернулли
y uv
x
dv
dx
v
x
dv
dx
1
v x v x
1 du
1
u
u2
x
xu 2
2 ln x
x dx
x
x
x
1
ln x 1 cx
u
x
1
y
ln x 1 cx
15.
Дифференциальные уравнения, неразрешенные относительноF ( x ,y ,
y имеют вид:
dy
) 0
dx
Если в некоторой точке M(xo,yo) уравнение F(xo,yo,p) = 0, где p = y’, имеет n
действительных корней, причем F(x,y,p) со своими первыми производными непрерывна
при x = xo, y = yo p = pi и дF / дx не обращается в ноль, то через точку M проходит n
интегральных кривых.
Если данное уравнение возможно разрешить относительно производной, то оно
распадается на n уравнений рассмотренного ранее вида, решив которые, получим
уравнения n семейств интегральных кривых.
Если уравнение можно представить в виде x ( y , y ) или y ( x , y ) , то
обозначая y’ = p, и рассматривая p как вспомогательную переменную, после
дифференцирования по y или x получим уравнение относительно dp/dy или dp/dx ,
разрешенные относительно производной. Искомое решение получим в
параметрической форме.
16.
@Решить дифференциальное уравнение
dy dy
x y
dx dx
2
Решение
dy
p
dx
x py p 2
dy
py
2 p2
2
dp 1 p
1 p2
Линейное неоднородное уравнение
dx
1
dy
p
dp
1
p ( y 2p)
p
dy
C arcsin p
y p
1 p2
x py p 2















 Математика
Математика








