Свойства гетерогенных систем. Эффективная диэлектрическая проницаемость

1. свойства гетерогенных систем. Эффективная диэлектрическая проницаемость. Схематичные изображения двухкомпонентных гетеро-

свойства гетерогенных систем.
Эффективная диэлектрическая проницаемость.
Схематичные изображения двухкомпонентных гетеросистем: матричная гетеросистема (а) и статистическая
гетеросистема (б)
а
В этом случае эффективная диэлектрическая проницаемость εeff
композитной среды определяется уравнением
D= ε0εeff E
где D — средняя макроскопическая (усредненная по объему) величина вектора электрической индукции,
E — средний по объему вектор напряженности электрического поля в среде.
Эффективная диэлектрическая проницаемость εeff может быть комплексной и,
в случае анизотропных сред, тензорной величиной.
1

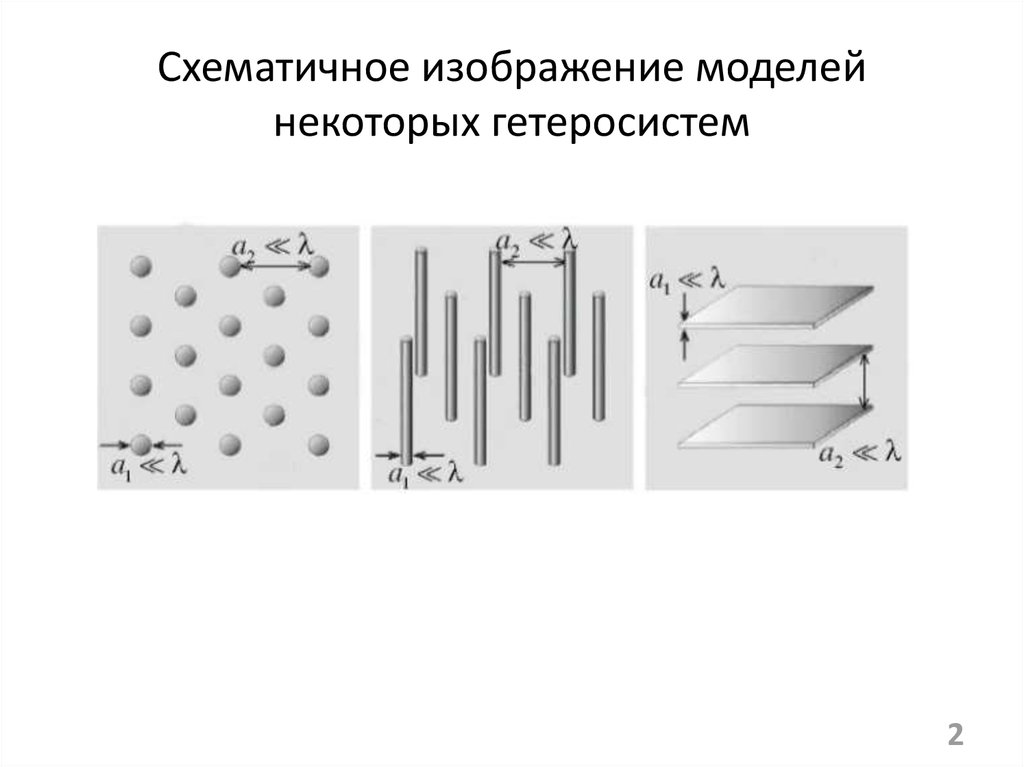
2. Схематичное изображение моделей некоторых гетеросистем

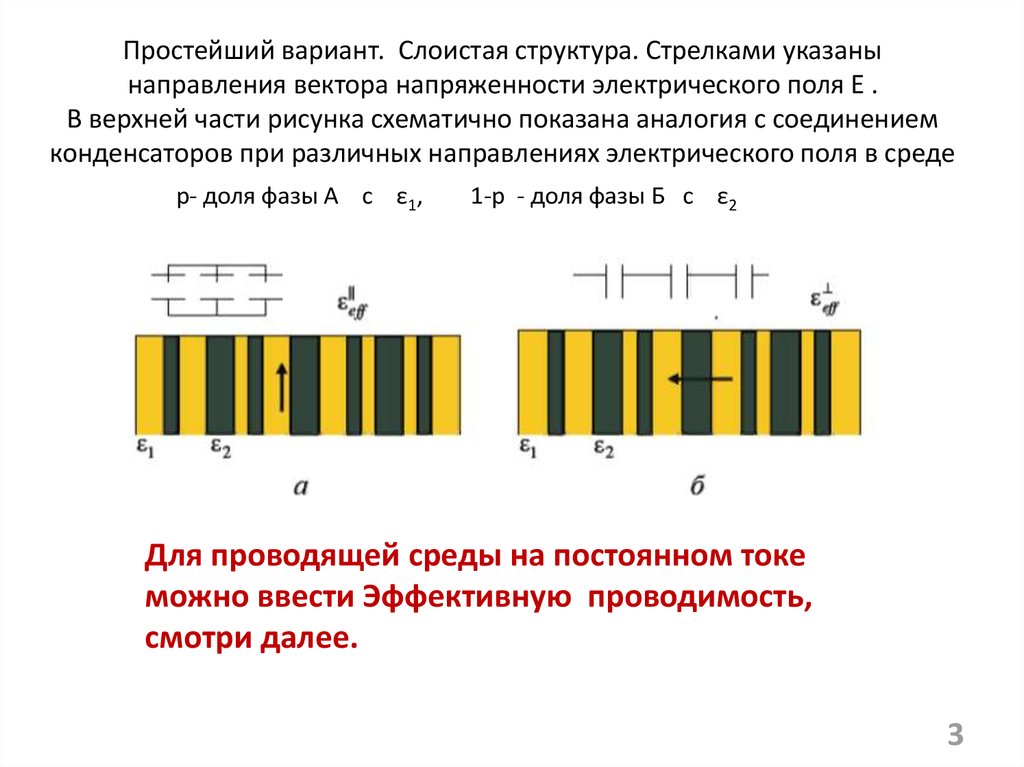
2

3. Простейший вариант. Слоистая структура. Стрелками указаны направления вектора напряженности электрического поля E . В верхней

части рисунка схематично показана аналогия с соединением
конденсаторов при различных направлениях электрического поля в среде
р- доля фазы А с ε1,
1-р - доля фазы Б с ε2
Для проводящей среды на постоянном токе
можно ввести Эффективную проводимость,
смотри далее.
3

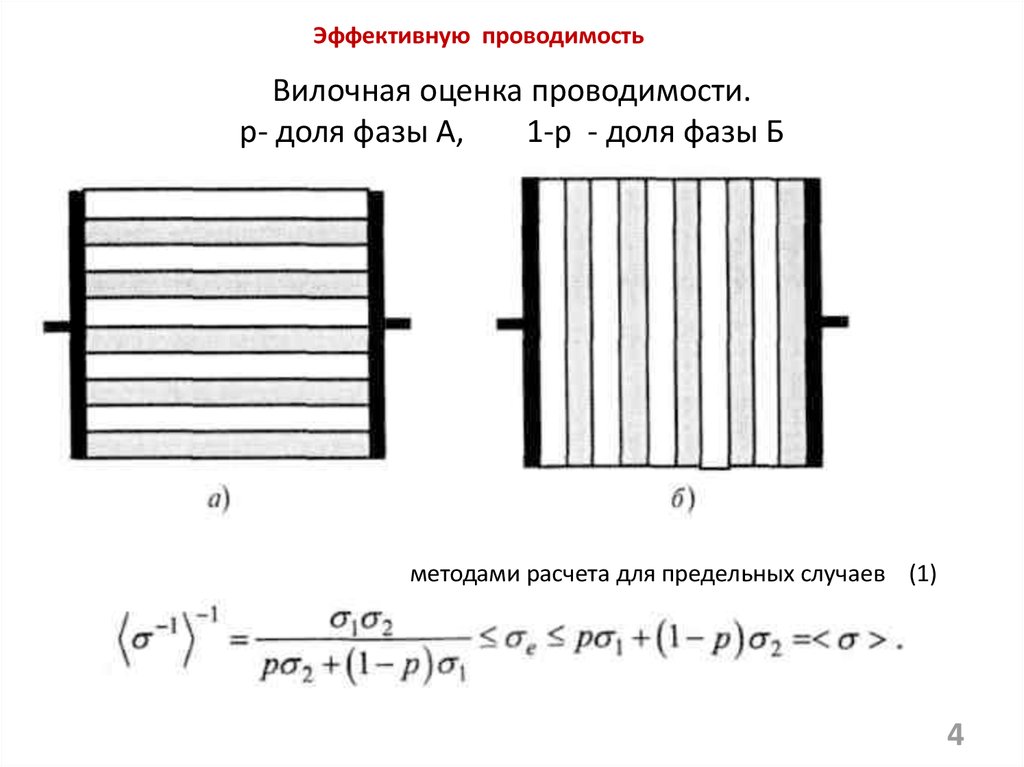
4. Вилочная оценка проводимости. р- доля фазы А, 1-р - доля фазы Б

Эффективную проводимость
Вилочная оценка проводимости.
р- доля фазы А,
1-р - доля фазы Б
методами расчета для предельных случаев (1)
4

5. Вилочная оценка проводимости по результатам расчета различными методами: (1) и (2)-для случая сферических включений

5

6. В рамках приближения эффективной среды считается, что каждое из включений с диэлектрическими проницаемостями ε2 находится в

некоторой эффективной
среде. В первом приближении форма включений считается сферической, а учет
взаимодействия каждого шара со всеми окружающими его элементами
гетеросистемы заменяется учетом взаимодействия со средой,
характеризующейся эффективной диэлектрической проницаемостью εeff .
При этом делается предположение, что на каждый шар действует поле, которое
является усредненным по всему объему. В этом случае поля в каждом
сферическом компоненте с диэлектрической проницаемостью εi , задаются
выражением ниже, то есть однородны и
имеют одинаковое направление: (здесь номер i=2)
6

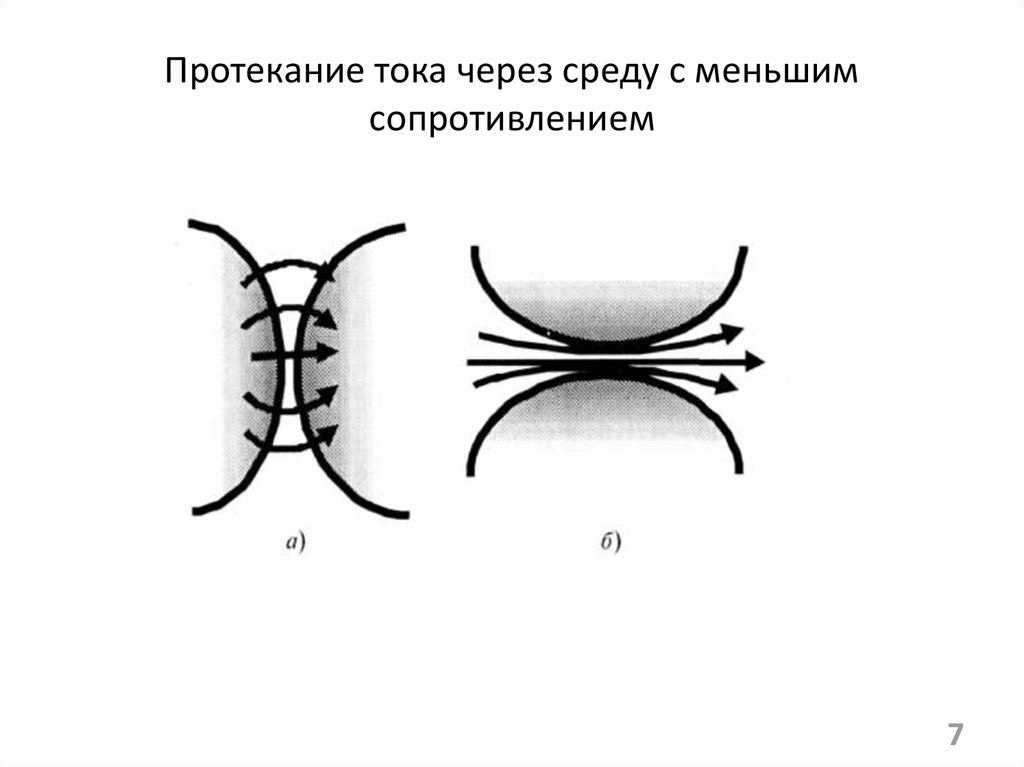
7. Протекание тока через среду с меньшим сопротивлением

7

8.

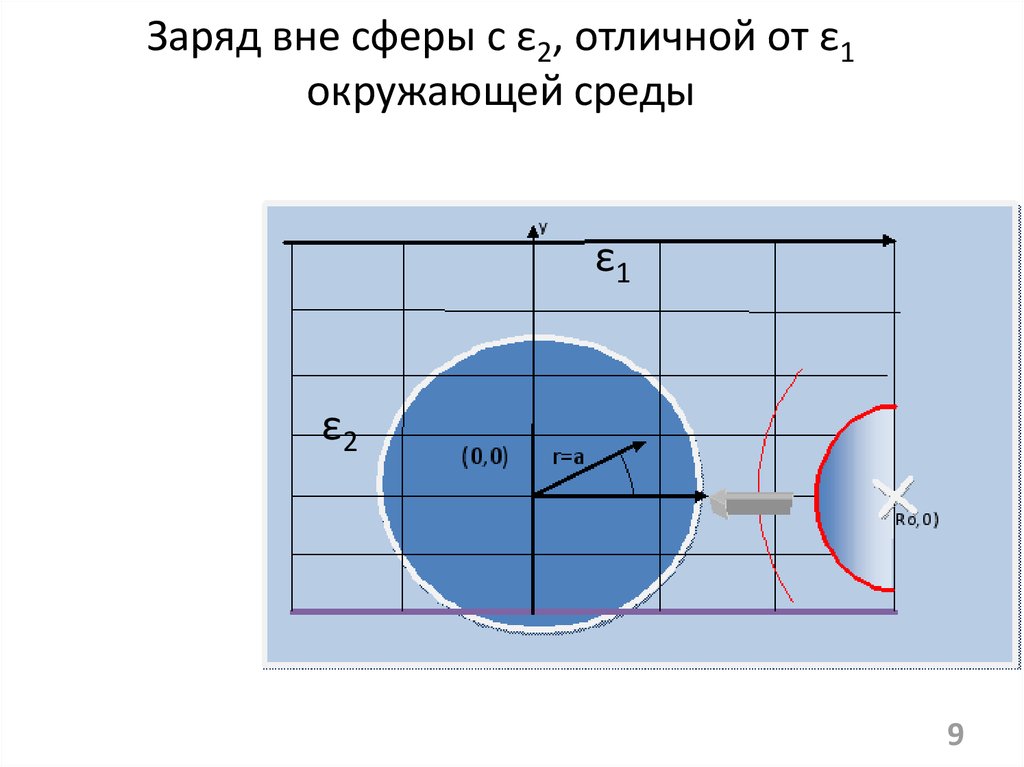
8

9. Заряд вне сферы с ε2, отличной от ε1 окружающей среды

ε1
ε2
9

10.

M
r
R
θ
O
a
ro
р
10

11. Такое поле, искажаясь в окрестности шара, не изменяется и равно E на большом расстоянии от него. Иначе говоря, это поле,

существующее «на
бесконечности», то есть далеко от включения, в среде с диэлектрической
проницаемостью ε1.
Получим выражение для напряженности электрического поля
внутри шара. Найдем вначале распределение потенциала в
рассматриваемой системе. Выберем начало сферической системы
координат в центре шара. Будем искать потенциал вне шара ϕ в виде
суммы потенциала однородного приложенного поля и
дополнительного вклада в потенциал, вызываемого шаром. Второе
слагаемое
должно обращаться в нуль на бесконечности, зависеть только от
напряженности электрического поля E и являться решением уравнения
Лапласа ∆φ = 0 . Можно показать, что данным условиям удовлетворяет
единственная сумма, где А – некая константа:
φ = −(E,r )+ A/r3
(1.58)
Потенциал поля внутри шара ϕ1 будем искать в виде
φ1 = -B(E,r ),
(1.59)
11

12.

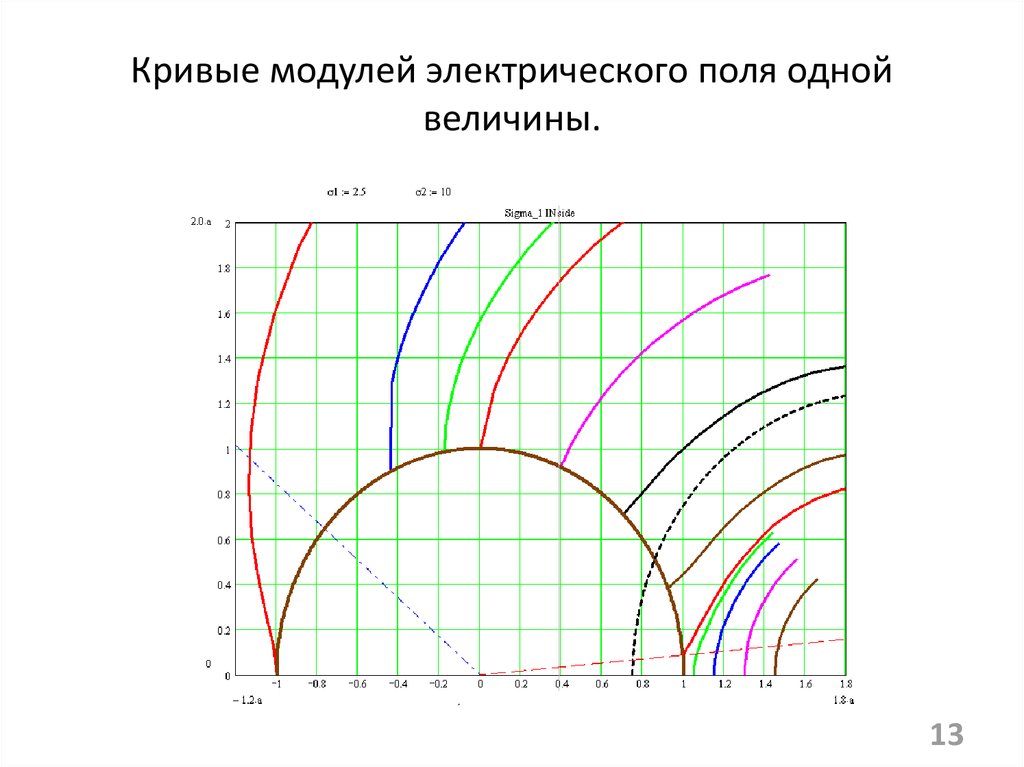
12

13. Кривые модулей электрического поля одной величины.

13

14. Кривые модулей электрического поля одной величины

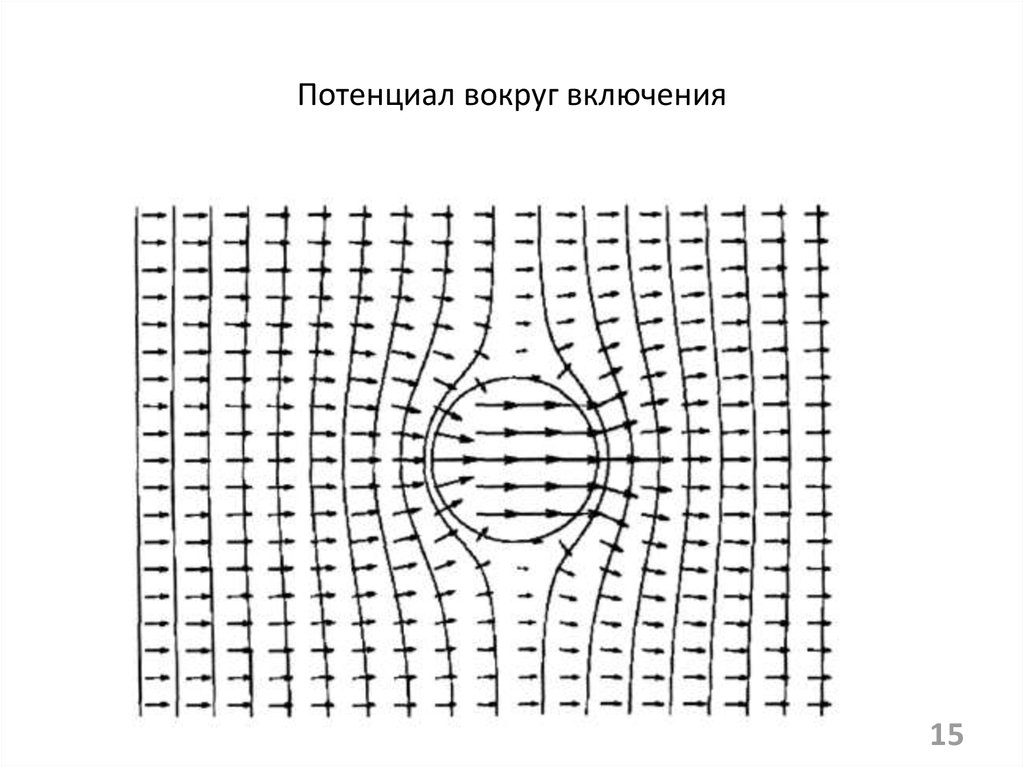
14

15. Потенциал вокруг включения

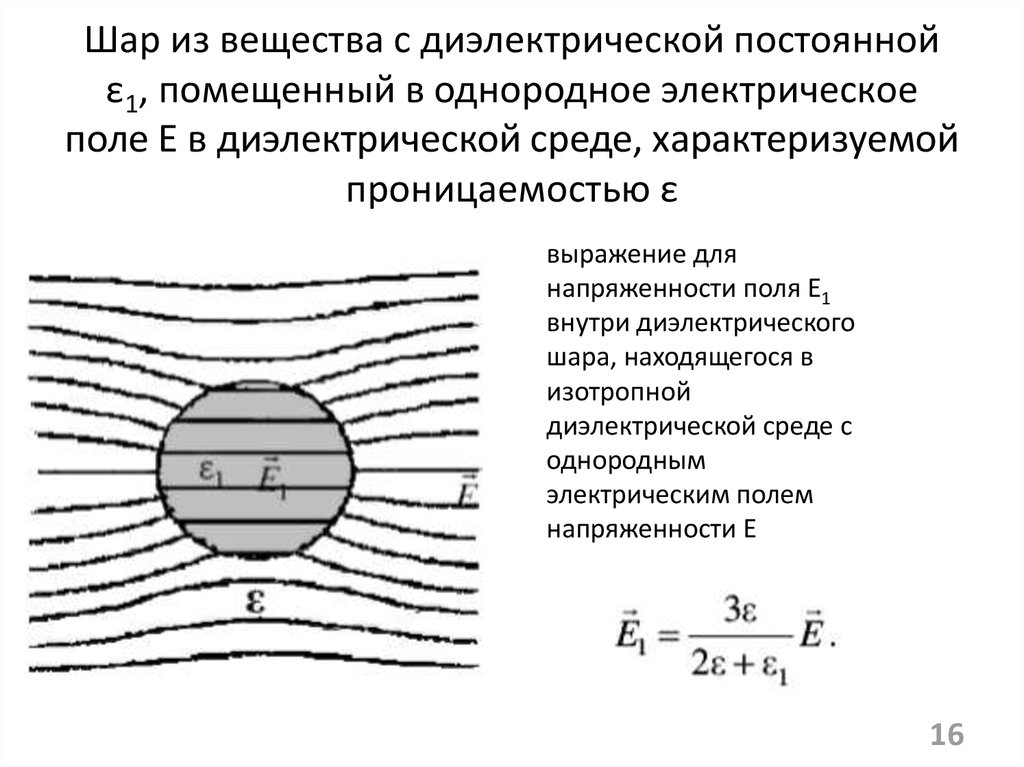
15

16. Шар из вещества с диэлектрической постоянной ε1, помещенный в однородное электрическое поле E в диэлектрической среде,

характеризуемой
проницаемостью ε
выражение для
напряженности поля E1
внутри диэлектрического
шара, находящегося в
изотропной
диэлектрической среде с
однородным
электрическим полем
напряженности E
16

17.

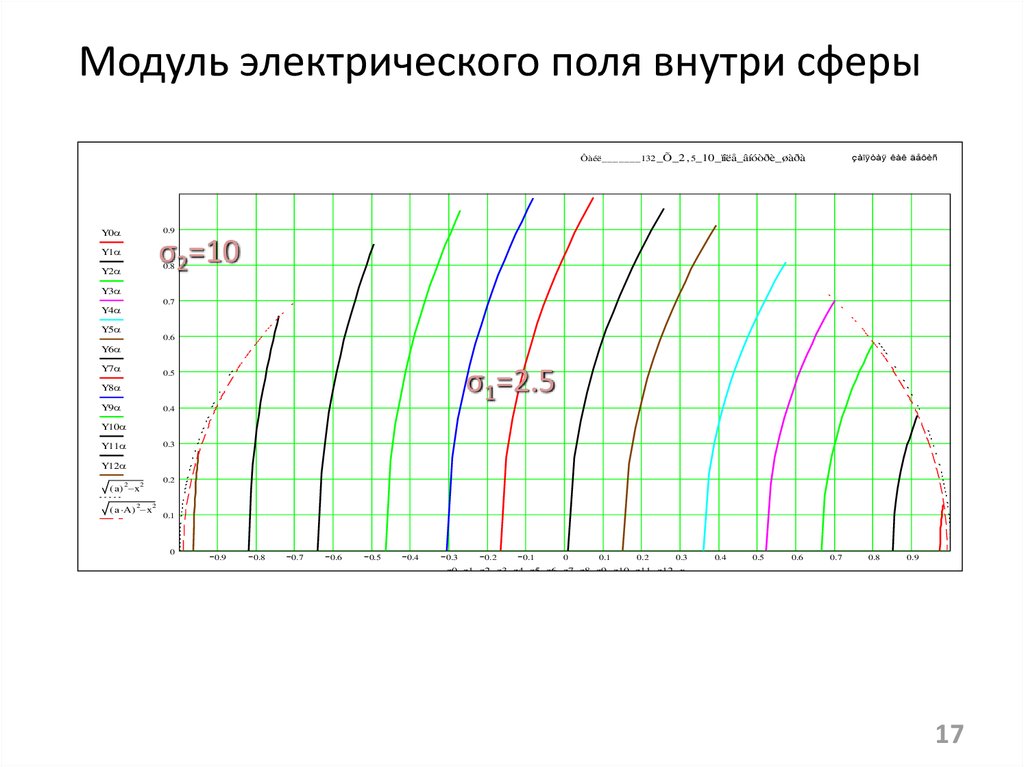
Модуль электрического поля внутри сферы
Ôàéë_______132 _Õ_2 5_10_ïîëå_âíóòðè_øàðà
çàïÿòàÿ êàê äåôèñ
0.9
Y0
σ2=10
Y1
0.8
Y2
Y3
0.7
Y4
Y5
0.6
Y6
Y7
σ1=2.5
0.5
Y8
Y9
0.4
Y10
0.3
Y11
Y12
0.2
( a) x
2
2
( a A) x
2
2
0.1
0
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
z0 z1 z2 z3 z4 z5 z6 z7 z8 z9 z10 z11 z12 x
17

18.

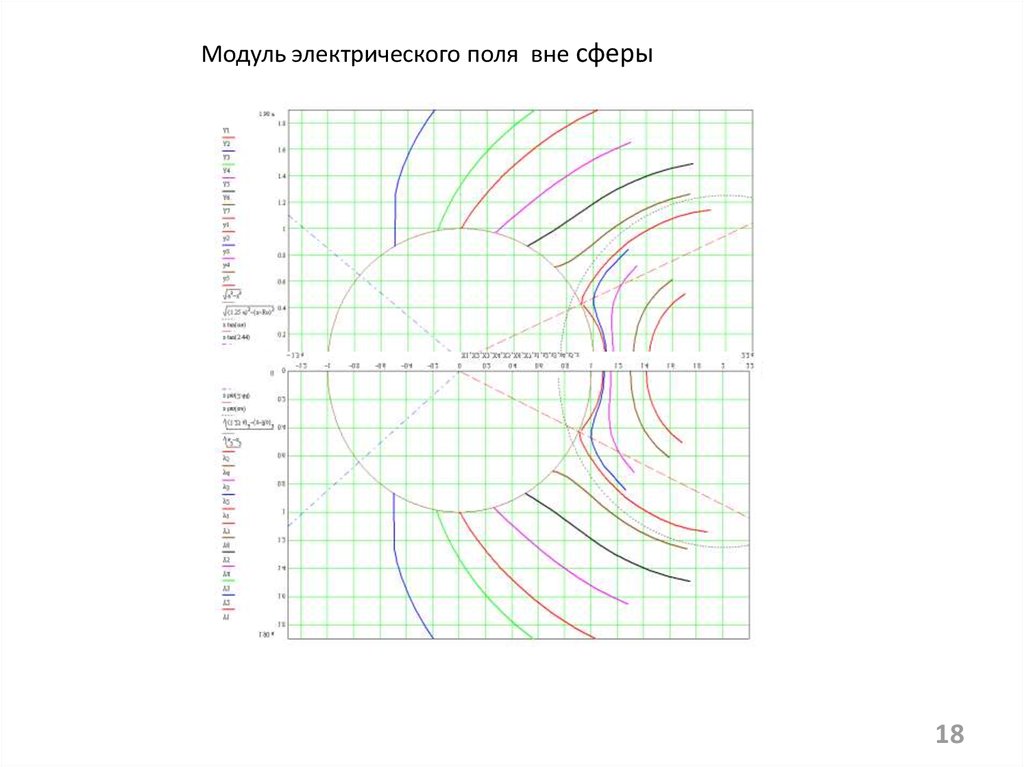
Модуль электрического поля вне сферы
18

19.

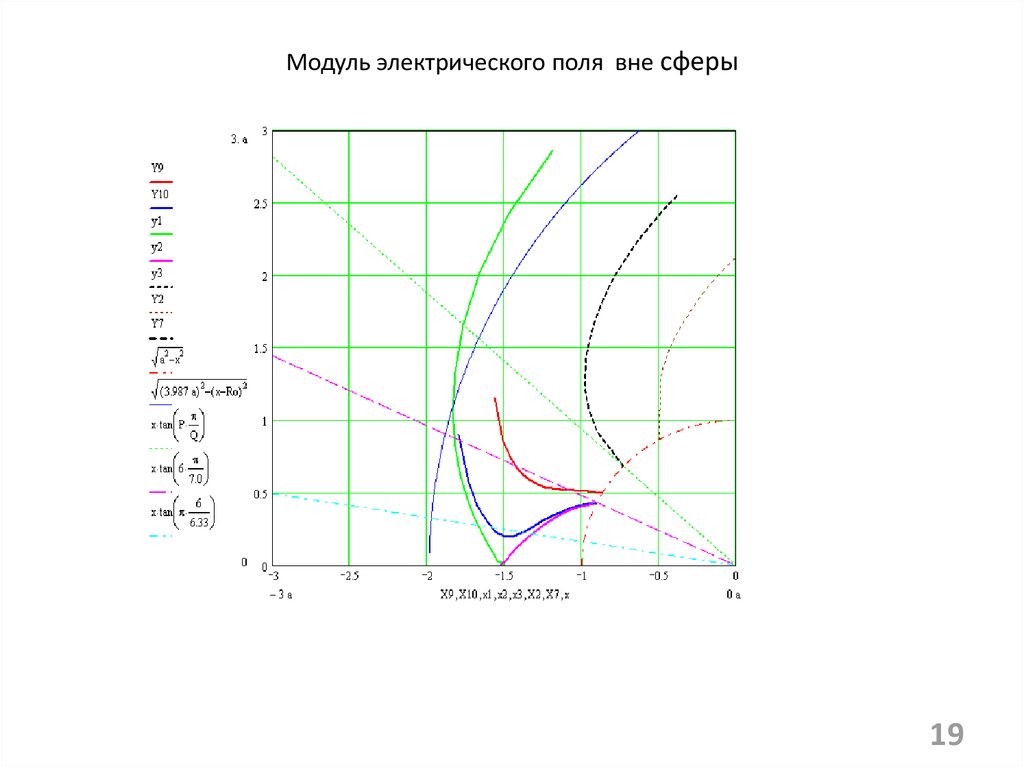
Модуль электрического поля вне сферы
19

20. К выводу величины вектора поляризации диэлектрического шара в однородном электрическом поле

20

21.

21