Похожие презентации:
Вывод линейных УУН для сети переменного тока. Идеальный коэффициент трансформации
1. Вывод линейных УУН для сети переменного тока
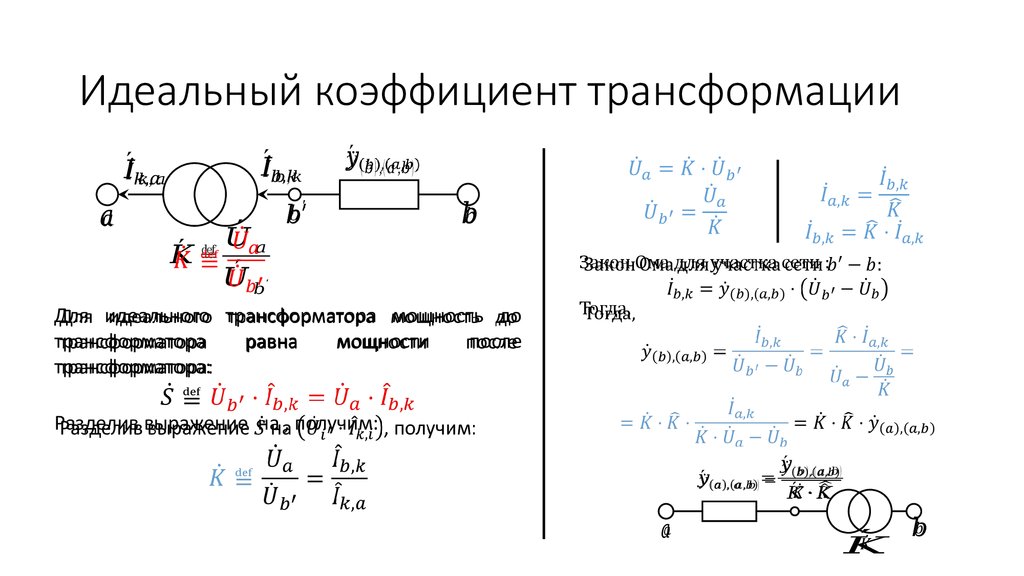
Лекция 12. Идеальный коэффициент трансформации
´,
´
,
´ ( ) , ( , )
′
´
´ ≝
´
Закон Ома для участка сети :
′
Для идеального трансформатора мощность до
трансформатора
равна
мощности
после
трансформатора:
Тогда,
Разделив выражение на , получим:
´ ( ) , ( , )
´ ( ), ( , )=
^
´ ⋅
´
3. Обозначения параметров сети
•• - число узлов сети.• - проводимость между узлами с номером и . Когда нет связи между узлами и , тогда
• - комплексный коэффициент трансформации между узлами и , относящийся к узлу . Когда
коэффициента трансформации нет, тогда
• - комплексный коэффициент трансформации между узлами и , относящийся к узлу . Когда
коэффициента трансформации нет, тогда
• - проводимость на землю узла . Когда нет этой проводимости, .
• - напряжение узла . В случае трехфазной сети – линейное.
• - ток потребления (или генерации) узла . В случае трехфазной сети – фазный.
• - мощность потребления (или генерации) узла . В случае трехфазной сети – суммарная по
трем фазам.
4. Изображение обобщенной ветви сети переменного тока
´´
=
,( , )
´
´ ( , )
′
′
′
´
´
=
,( , )
´
′
´
,( , ) =
´
,( ,
) =
^
,( ,
^
´ ( , )
´
⋅
)
´ ( ,
,( ,
´
⋅(
, ( , )
´ −
´ )
⋅
, ( , )
´
´ −
´
⋅(
⋅
,( , )
)
´
)⋅
,( , )
)
5. Изображение обобщенного узла сети переменного тока
´,( ,∗)
´
,( ,∗)
´
,( ,∗) ´
,( ,∗)
´ /
´
Первый закон Кирхгофа для некоторого узла :
С учетом того, что
Перепишем первый закон Кирхгофа для узла :
´
токи ветвей
Преобразуем это выражение, группируя согласные относительно :
6. Вывод матрицы проводимости для сети переменного тока. Уравнения установившегося режима (УУН)
С предыдущего слайда:Эту систему уравнений можно записать в матричном виде:
где - полная матрица проводимости,
7. Изображение обобщенного узла сети переменного тока K ̇_(i,(i,j))=1,∀i
Изображение обобщенного узла сетипеременного тока
´
,( ,∗)
´
,( ,∗)
´
,( ,∗) ´
,( ,∗)
´ /
´
Первый закон Кирхгофа для некоторого узла :
С учетом того, что
Перепишем первый закон Кирхгофа для узла :
´
токи ветвей
Преобразуем это выражение, группируя согласные относительно :
8. Вывод матрицы проводимости для сети переменного тока. Уравнения установившегося режима (УУН) K ̇_(i,(i,j))=1,∀i
Вывод матрицы проводимости для сетипеременного тока. Уравнения установившегося
режима (УУН)
С предыдущего слайда:
Эту систему уравнений можно записать в матричном виде:
где - полная матрица проводимости,
9. Понятия базисного и балансирующего узлов
Полная матрица проводимости:
1. Плохо обусловлена, в лучшем случае, и вырождена – в худшем, ввиду значений ее составляющих для задач в
реальной энергосистеме и ввиду самой структуры составления уравнений.
2. При условии наличия только действительных , является симметричной. Иначе – имеет симметричный портрет
(симметричное заполнение).
3. Слабо заполнена (бОльшая часть элементов равна нулю), ввиду малого количества связей в реальной энергосистеме.
1.=> Решение СЛУ в лучшем случае имеет неудовлетворительную точность, в худшем – не имеет решения вовсе. С этим
справляются тем, что вводят такие понятия, как базисный узел и балансирующий узел.
Базисный узел – это такой узел , для которого считается известным. Относительно него будут рассчитываться
напряжения всех остальных узлов. Тем самым, в полной матрице проводимости вычеркивается его столбец. Если
базисный узел всего один,
Балансирующий узел – это такой узел , для которого считается неизвестным. Весь небаланс тока в общей энергосистеме
будет скомпенсирован этим узлом. Тем самым, в полной матрице проводимости вычеркивается его строка, а может
быть тривиально найдена из напряжения остальных узлов после расчета.
Теоретически, можно ввести множество как базисных, так и балансирующих узлов. На практике расчетов, базисным и
балансирующим узлом обычно выбирается один и тот же узел. Для него из матрицы проводимости вычеркивается и его
строка, и его столбец.
10. Преобразование УУН при вводе базисного и балансирующего узлов. Пояснение обозначений
•Если в некоторой сети узлов, причем узел с номером –базисный, тогда:
- полная матрица проводимости
- матрица проводимости без строки балансирующего узла
- матрица проводимости без строки балансирующего и
столбца базисного узла
11. Преобразование УУН при вводе базисного и балансирующего узлов. Пояснение обозначений
-• вычеркнутый столбец базисного узла, вектор проводимостей с базисным узлом- полный вектор напряжений
- вектор напряжений без напряжения базисного узла
- полный вектор токов
- вектор токов без тока балансирующего узла
12. Преобразование УУН при вводе базисного и балансирующего узлов. Линейная форма записи УУН для переменного тока
•Решаемая система уравнений (красным помечены неизвестные)может быть записана в любом из представленных видов:
13. Декартовы и полярные координаты для параметров систем УУН
- Декартовы координаты для напряжений- Полярные координаты для напряжений
- Декартовы координаты для токов
- Полярные координаты редко встречаются
для записи токов.
- Декартовы координаты для проводимостей
- Полярные координаты для проводимостей
14. Запись линейной системы УУН в действительных числах в декартовой системе координат
Введем параметры сети в декартовых координатахОсновная идея вывода –
равенство мнимых и
действительных составляющих
Раскроем скобки, сгруппируем относительно
Запишем в виде равенств действительных и мнимых составляющих
15. Запись линейной системы УУН в действительных числах в декартовой системе координат. Матричная запись
Введем параметры сети в декартовых координатах
Раскроем скобки, сгруппируем относительно
Запишем в виде равенств действительных и мнимых составляющих
16. Конец
17.
−1∑
=1
( ( , ⋅ − , ⋅ ) + ⋅ ( , ⋅ + , ⋅ )) =( − , ⋅ )+ ⋅ ( + , ) ⋅ , =1 …( −
′
′′
′
′′
′
′
′′
′
18. Изображение обобщенной ветви сети переменного тока
´ ( , )′
´
´
=
,( , )
´
′
´ ,( , ) ´ ,( , )
′
´
´ ,( , )=
´
′
´ , ( , )
´ ( , )
´
´ −
´
´
⋅ +
⋅ (
,( , ) ⋅ )
^
^
´
´
,( , ) ⋅
,( , ) ⋅ , ( , )
,( , )
´ , ( , )
´ ( , )
´
´ +
´ −
´
´
⋅
⋅(
,( , ) =
,( , ) ⋅ )
^
^
´
´
⋅
⋅
´
,( , ) =
,( , )
,( , )
,( , )
,( , )
19. Предпосылки вывода
•Пусть в энергосистеме переменного тока узлов, причем узел сномером – базисный. Тогда линейная система УУН для нее
может быть записана как:
Или в матричной форме:















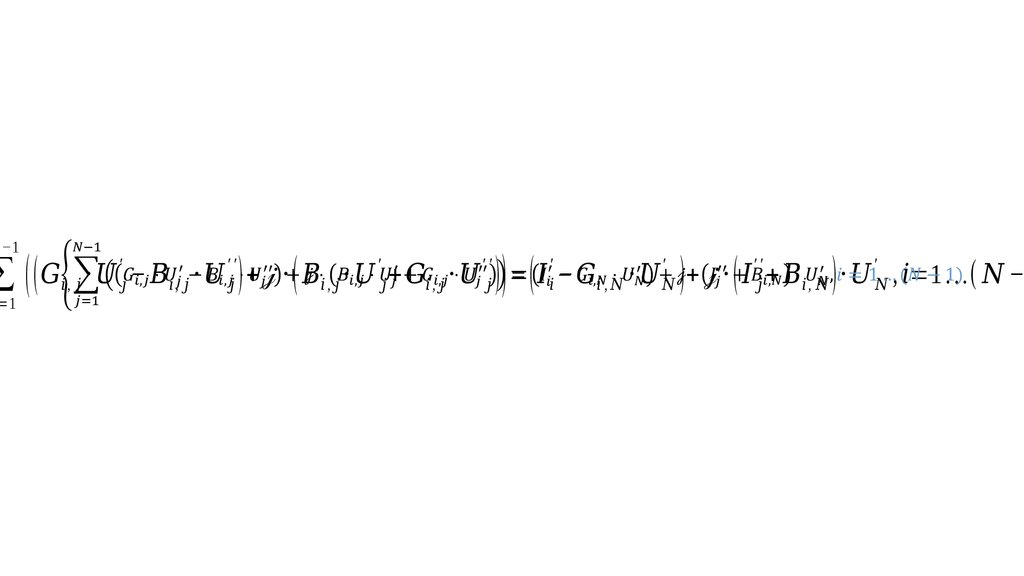


 Физика
Физика








