Проекційне креслення

1.

Тема:
«Проекційне креслення»

2.

Проекційне креслення
Проекційне креслення вивчає способи
побудови
на
площині
зображення
предметів, що мають три виміри.
За допомогою цих зображень можна
відтворити форму предмета, його величину і положення.
Перед тим, хто вивчає курс креслення,
стоїть принаймні дві основні задачі:
1.Навчитися
за
певними
законами
будувати креслення різних предметів.
2.Уміти читати креслення будь-якого
виробу або деталі.
Для побудови зображень предметів
користуються
методом
проектування, тобто відкинутим його
зображенням на площину.

3.

Проекційне креслення

4.

Проекційне креслення вивчає способи побудови
на площині зображення предметів, що мають
три виміри.

5.

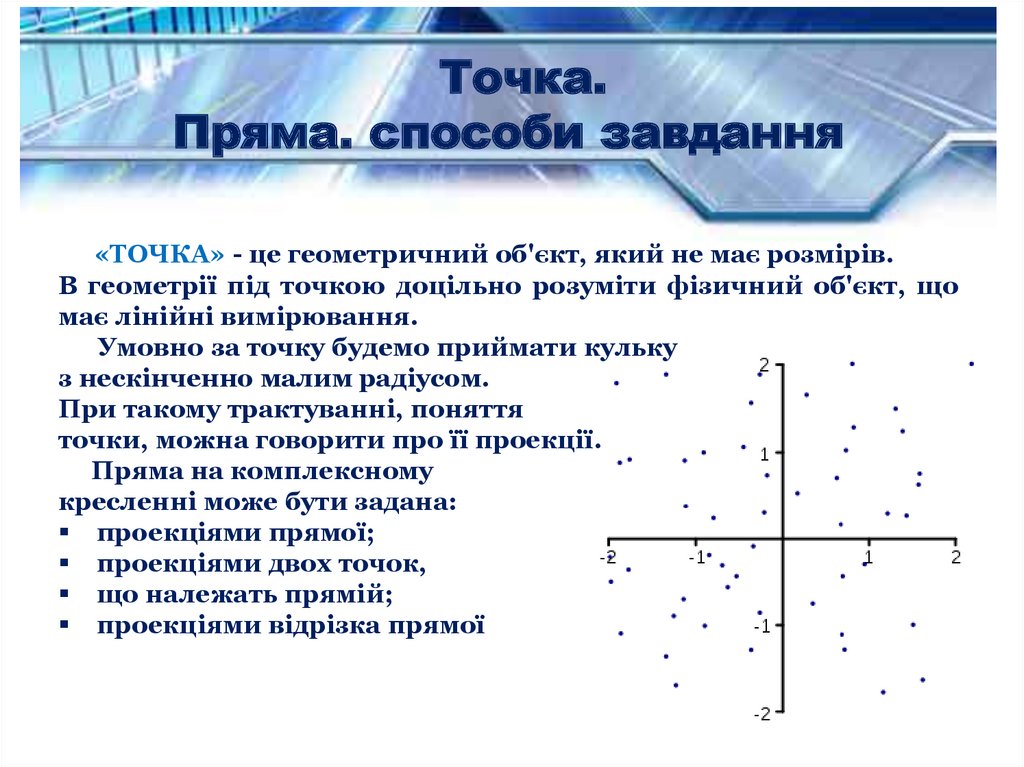
Точка.
Пряма. способи завдання
«ТОЧКА» - це геометричний об'єкт, який не має розмірів.
В геометрії під точкою доцільно розуміти фізичний об'єкт, що
має лінійні вимірювання.
Умовно за точку будемо приймати кульку
з нескінченно малим радіусом.
При такому трактуванні, поняття
точки, можна говорити про її проекції.
Пряма на комплексному
кресленні може бути задана:
проекціями прямої;
проекціями двох точок,
що належать прямій;
проекціями відрізка прямої

6.

Предмет і метод
нарисної геометрії
ОСНОВНИЙ МЕТОД НАСКРІЗНОЇ
ГЕОМЕТРІЇ
МЕТОД ПРОЕКЦІЙ
Проекція – це зображення предмета
(відкинуте) на площину за допомогою
проектуючих променів. Спроектувати предмет – це означає зобразити його на
площині.
Розрізняють два види проекцій: центральні і
паралельні.
Процес
одержання
проекцій
називається проеціюванням.

7.

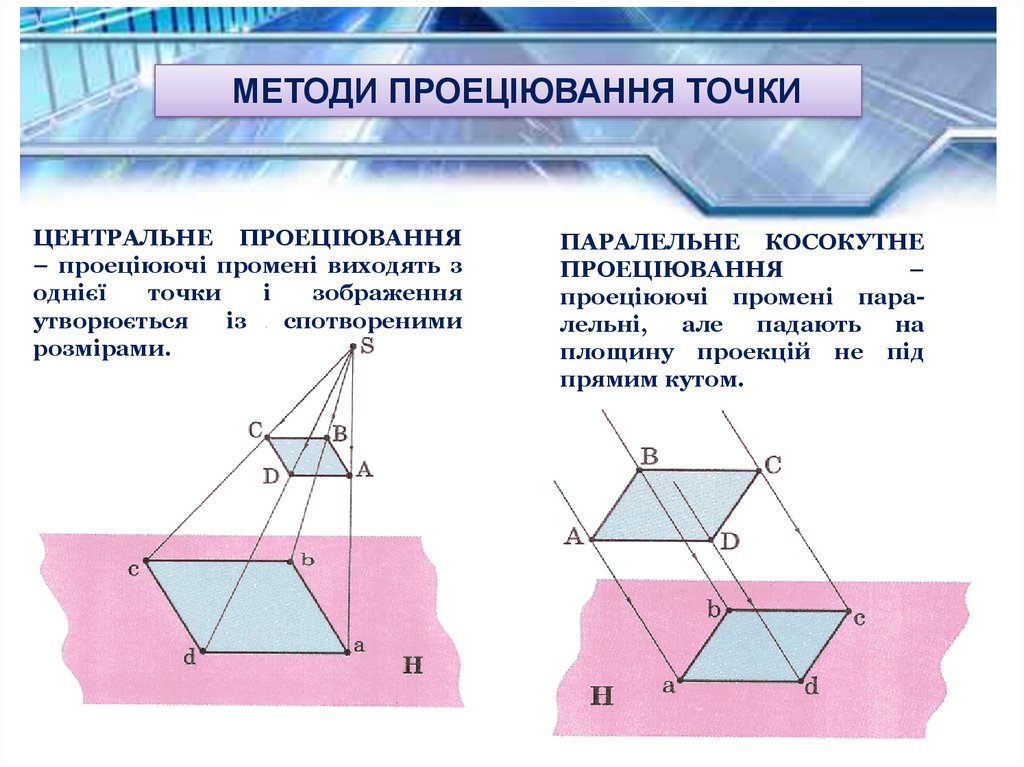
МЕТОДИ ПРОЕЦІЮВАННЯ ТОЧКИ
ЦЕНТРАЛЬНЕ ПРОЕЦІЮВАННЯ
– проеціюючі промені виходять з
однієї
точки
і
зображення
утворюється
із
спотвореними
розмірами.
ПАРАЛЕЛЬНЕ КОСОКУТНЕ
ПРОЕЦІЮВАННЯ
–
проеціюючі промені паралельні, але падають на
площину проекцій не під
прямим кутом.

8.

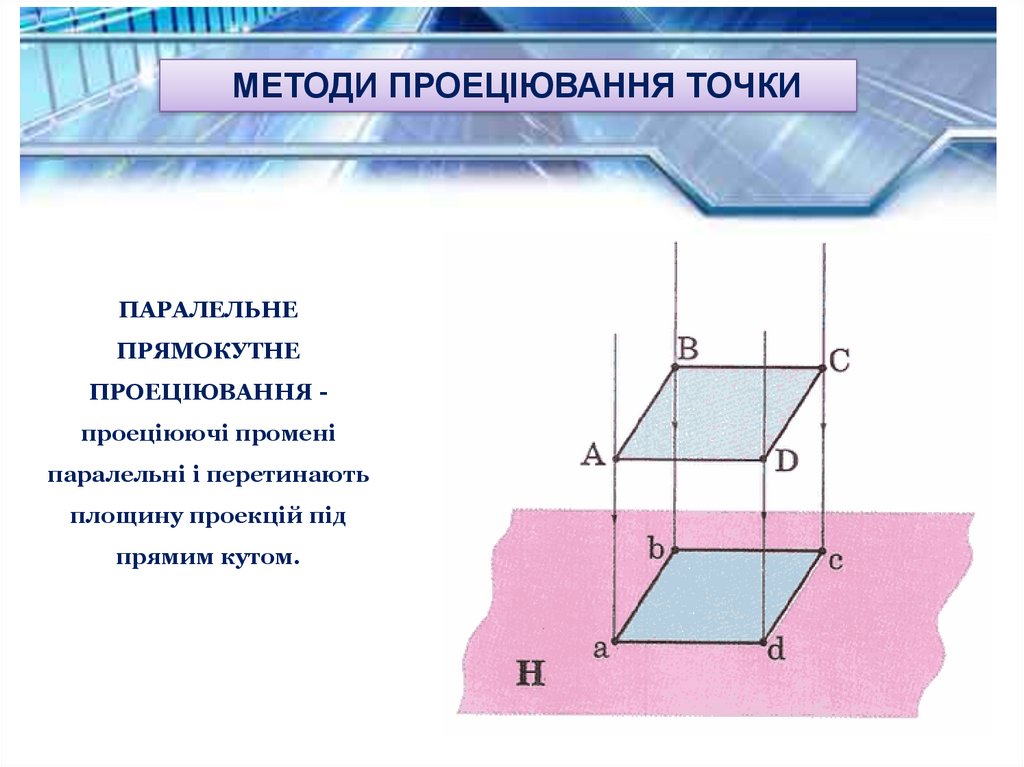
МЕТОДИ ПРОЕЦІЮВАННЯ ТОЧКИ
ПАРАЛЕЛЬНЕ
ПРЯМОКУТНЕ
ПРОЕЦІЮВАННЯ проеціюючі промені
паралельні і перетинають
площину проекцій під
прямим кутом.

9.

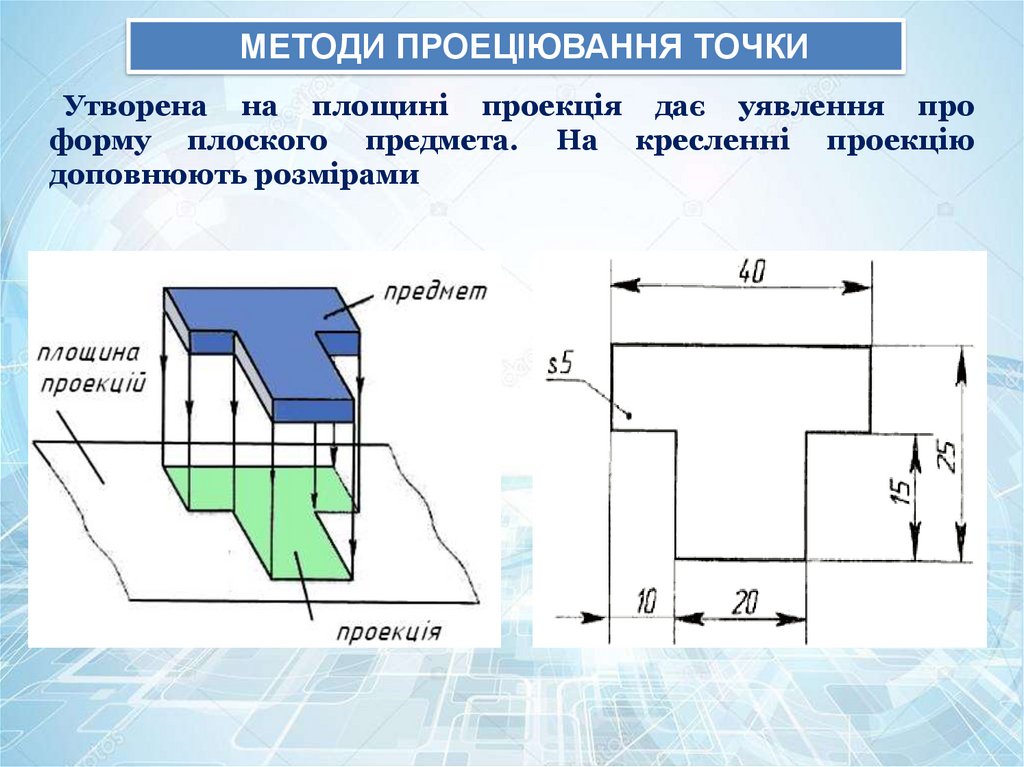
МЕТОДИ ПРОЕЦІЮВАННЯ ТОЧКИ
Утворена на площині проекція дає уявлення про
форму плоского предмета. На кресленні проекцію
доповнюють розмірами

10.

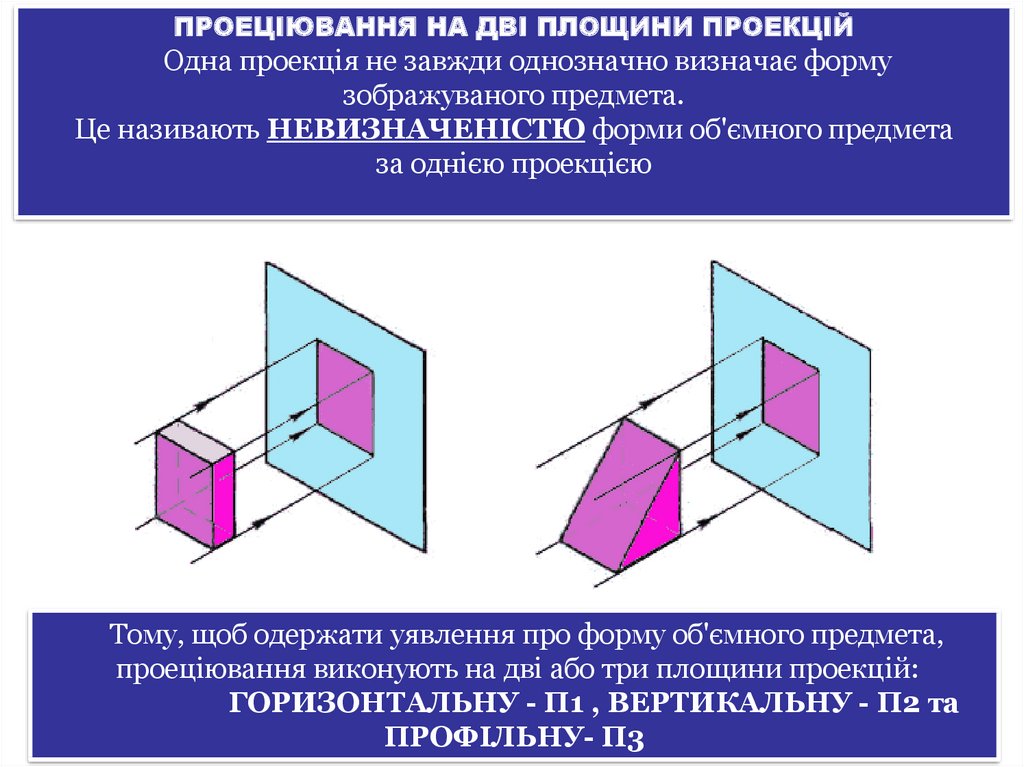
ПРОЕЦІЮВАННЯ НА ДВІ ПЛОЩИНИ ПРОЕКЦІЙ
Одна проекція не завжди однозначно визначає форму
зображуваного предмета.
Це називають НЕВИЗНАЧЕНІСТЮ форми об'ємного предмета
за однією проекцією
Тому, щоб одержати уявлення про форму об'ємного предмета,
проеціювання виконують на дві або три площини проекцій:
ГОРИЗОНТАЛЬНУ - П1 , ВЕРТИКАЛЬНУ - П2 та
ПРОФІЛЬНУ- П3

11.

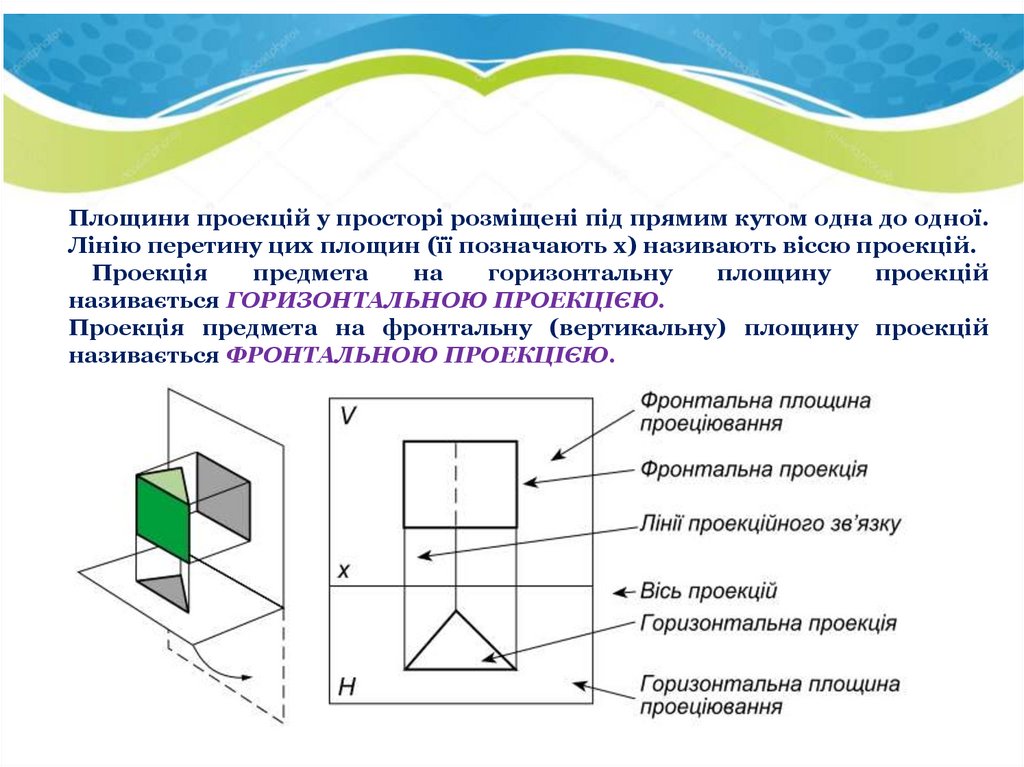
Площини проекцій у просторі розміщені під прямим кутом одна до одної.
Лінію перетину цих площин (її позначають х) називають віссю проекцій.
Проекція
предмета
на
горизонтальну
площину
проекцій
називається ГОРИЗОНТАЛЬНОЮ ПРОЕКЦІЄЮ.
Проекція предмета на фронтальну (вертикальну) площину проекцій
називається ФРОНТАЛЬНОЮ ПРОЕКЦІЄЮ.

12.

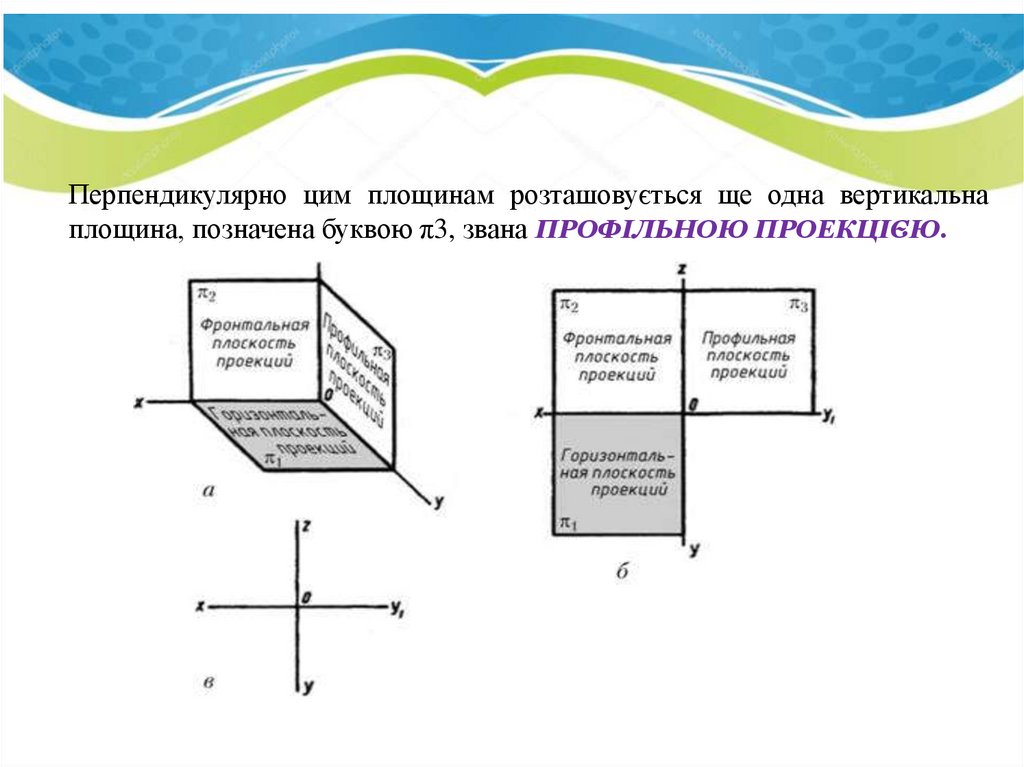
Перпендикулярно цим площинам розташовується ще одна вертикальна
площина, позначена буквою π3, звана ПРОФІЛЬНОЮ ПРОЕКЦІЄЮ.

13.

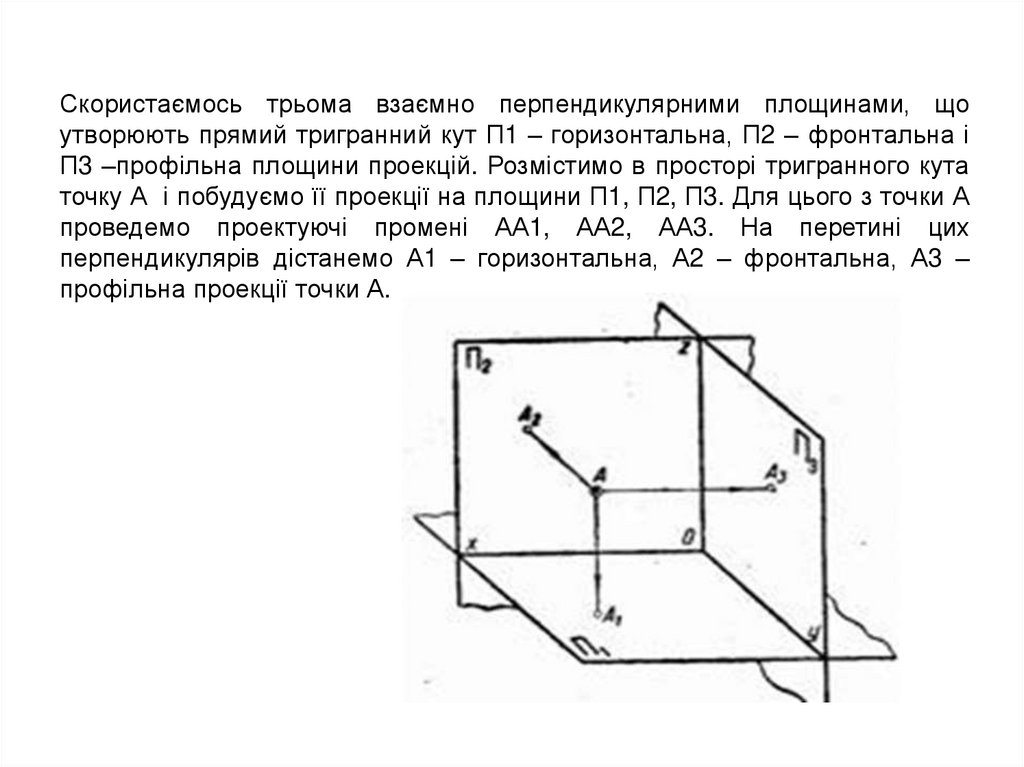
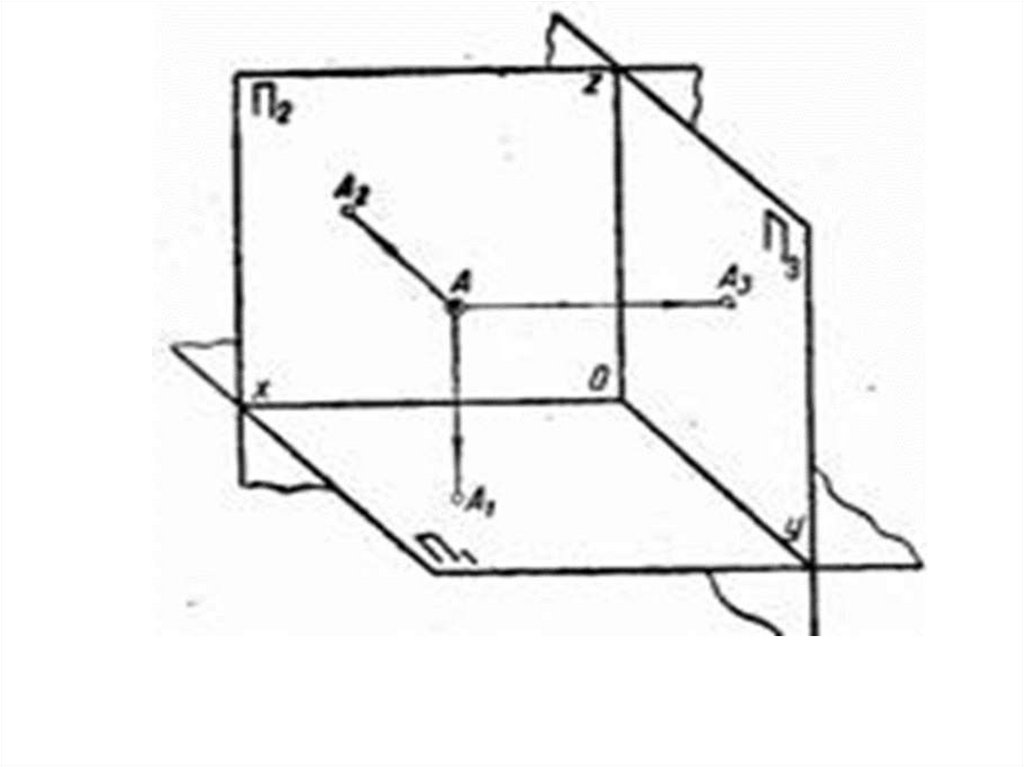
Скористаємось трьома взаємно перпендикулярними площинами, що
утворюють прямий тригранний кут П1 – горизонтальна, П2 – фронтальна і
П3 –профільна площини проекцій. Розмістимо в просторі тригранного кута
точку А і побудуємо її проекції на площини П1, П2, П3. Для цього з точки А
проведемо проектуючі промені АА1, АА2, АА3. На перетині цих
перпендикулярів дістанемо А1 – горизонтальна, А2 – фронтальна, А3 –
профільна проекції точки А.

14.

15.

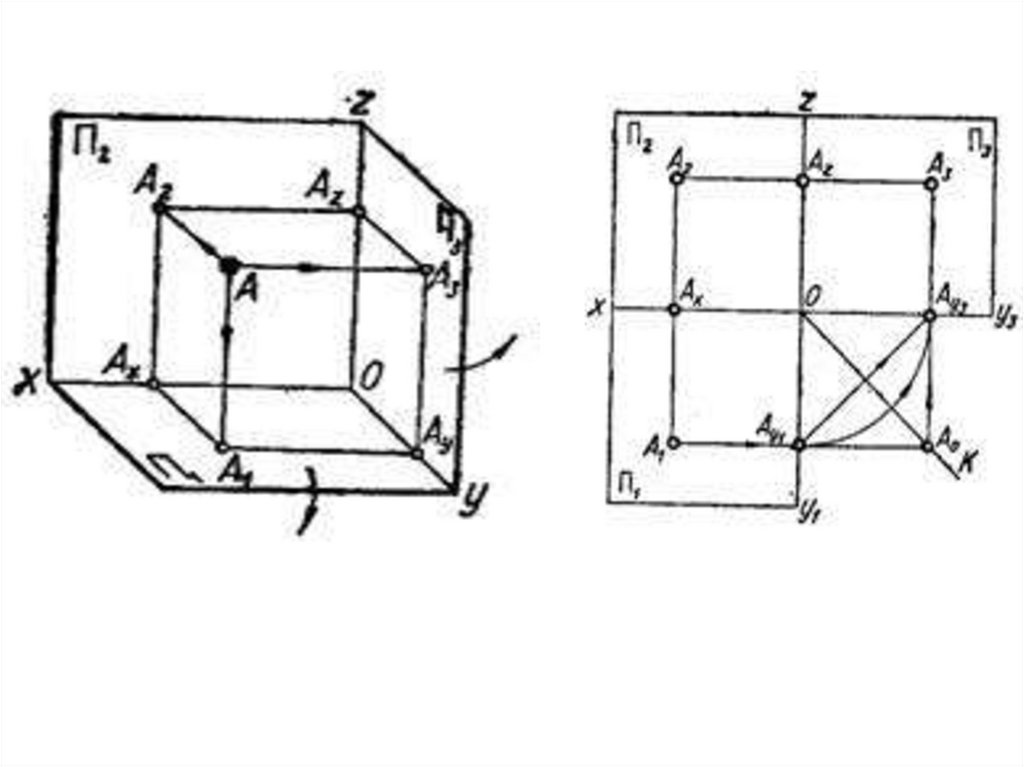
Комплексне креслення точки.
Від просторового зображення точки переходять до плоского
або комплексного креслення, яке утворюється в наслідок
обертання площин проекцій навколо осей, вважаючи
тригранний кут розщепленим по осі Оу і залишаючи
нерухомою площину П2, площину П1 повертають на 90°
вниз навколо осі Ох, а площину П3 на 90° навколо осі Оz
Таким чином утвориться плоске креслення разом з
побудованими на них проекціями А1, А2, А3- називається
комплексним кресленням. Для побудови профільної
проекції А3 використовують постійну лінію К, яка
проводиться під кутом 45°

16.

17.

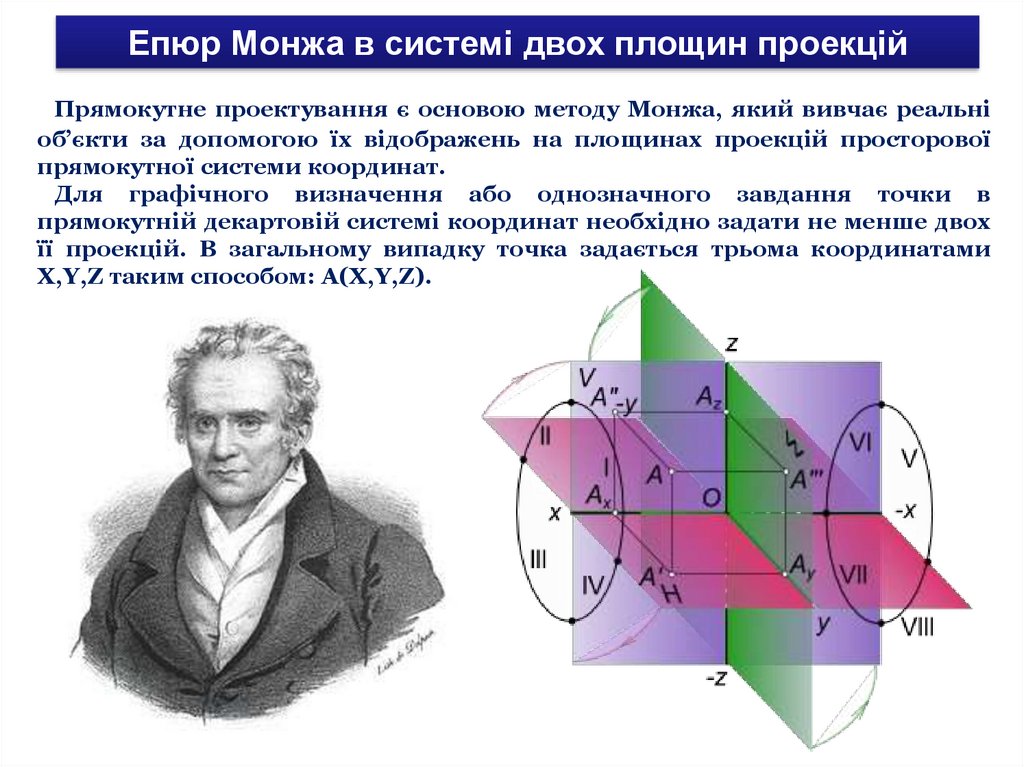
Епюр Монжа в системі двох площин проекцій
Прямокутне проектування є основою методу Монжа, який вивчає реальні
об’єкти за допомогою їх відображень на площинах проекцій просторової
прямокутної системи координат.
Для графічного визначення або однозначного завдання точки в
прямокутній декартовій системі координат необхідно задати не менше двох
її проекцій. В загальному випадку точка задається трьома координатами
X,Y,Z таким способом: A(X,Y,Z).

18.

Епюр Монжа в системі трьох площин проекцій
Побудова третьої проекції точки.
Тут можливі два випадки:
1) побудова профільної проекції;
2) побудова проекції точки на будь-яку нову площину –
заміна площин проекцій.

19.

20.

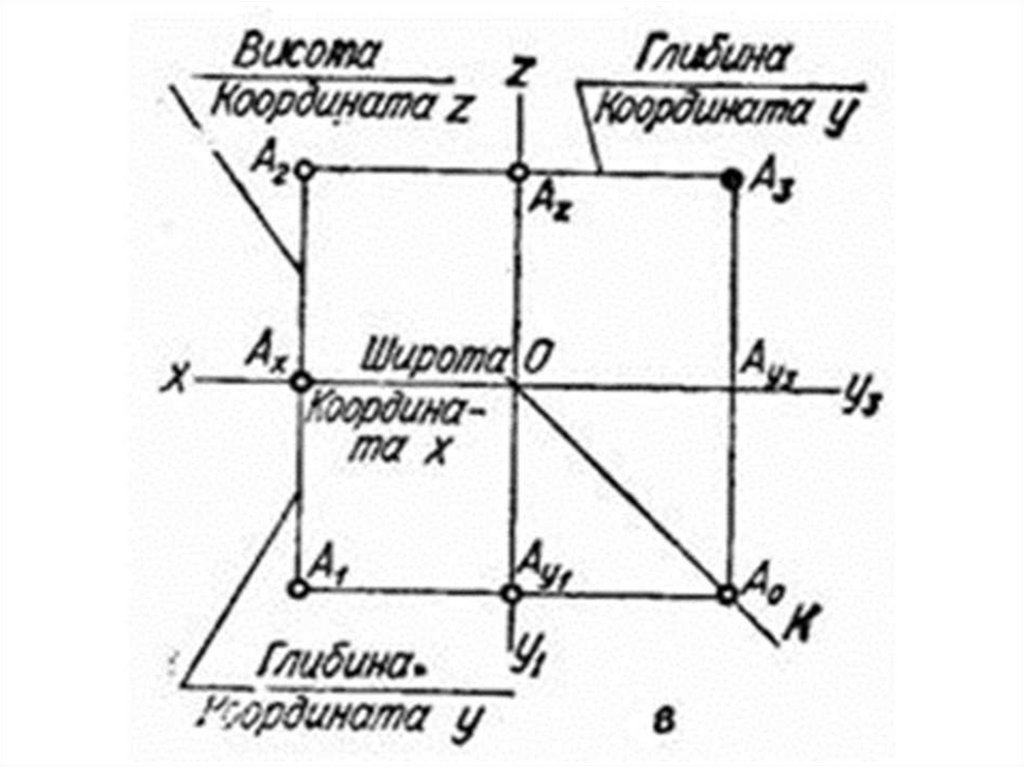
1. Висота
- це відстань
від осі Х вверх по осі Z.
2. Ширина - це відстань
від центра осей по осі Х.
3. Глибина - це відстань
від фронтальної
площини проекцій вниз
по осі У

21.

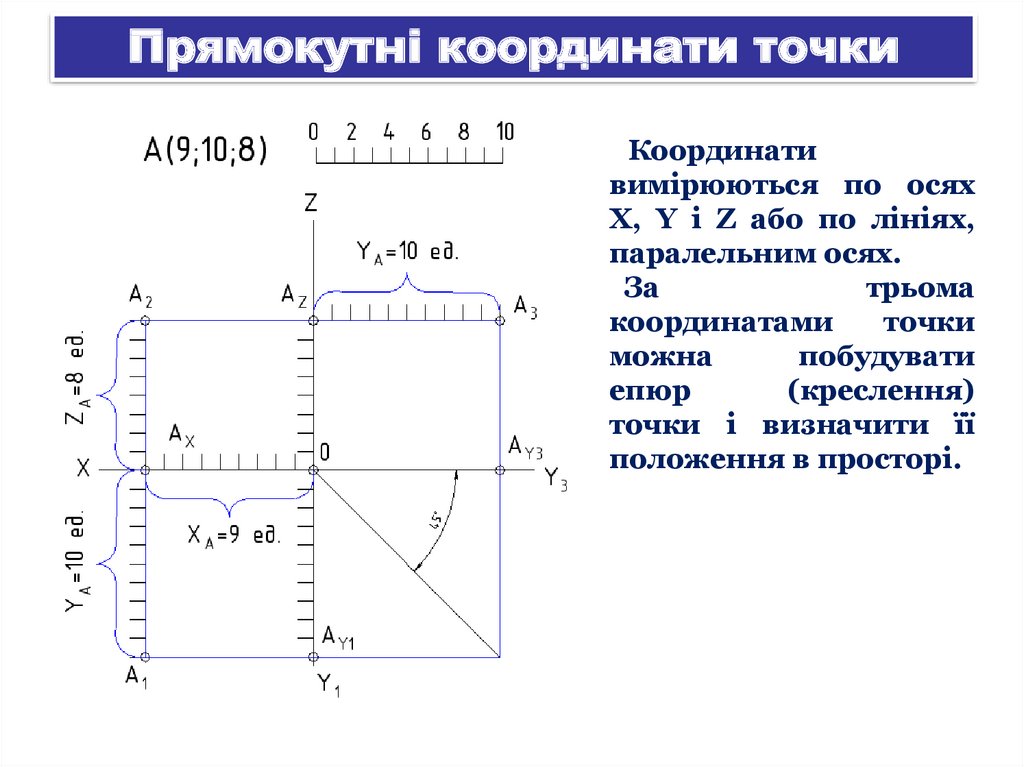
Прямокутні координати точки
Координати
вимірюються по осях
X, Y і Z або по лініях,
паралельним осях.
За
трьома
координатами
точки
можна
побудувати
епюр
(креслення)
точки і визначити її
положення в просторі.

22.

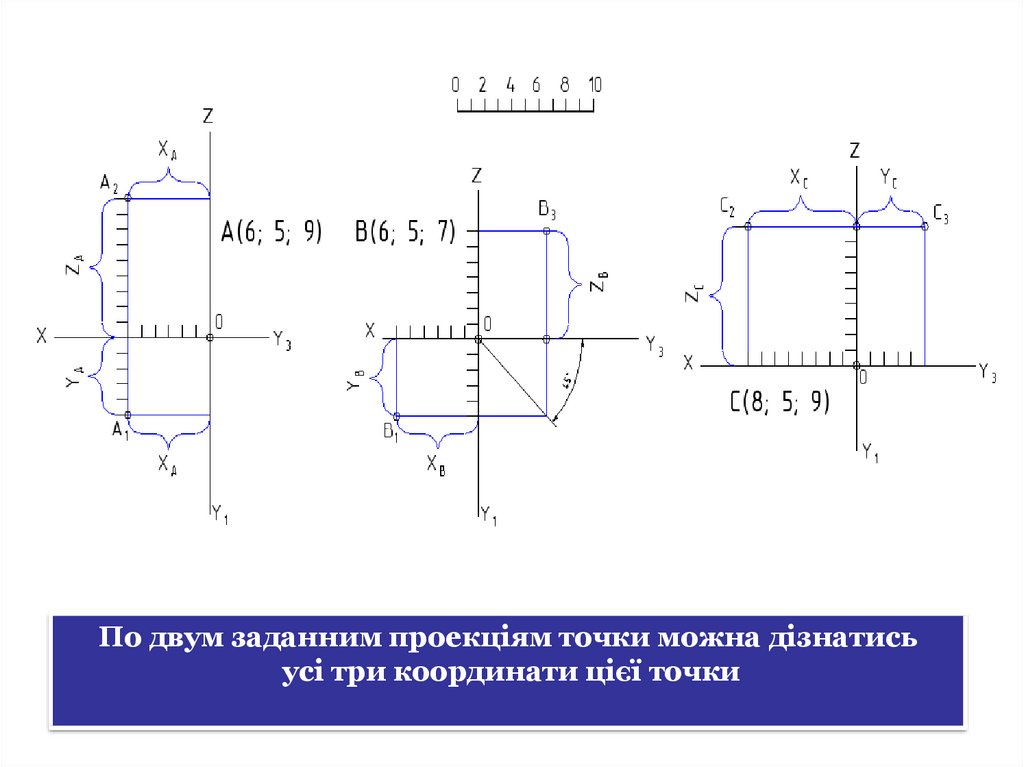
По двум заданним проекціям точки можна дізнатись
усі три координати цієї точки

23.

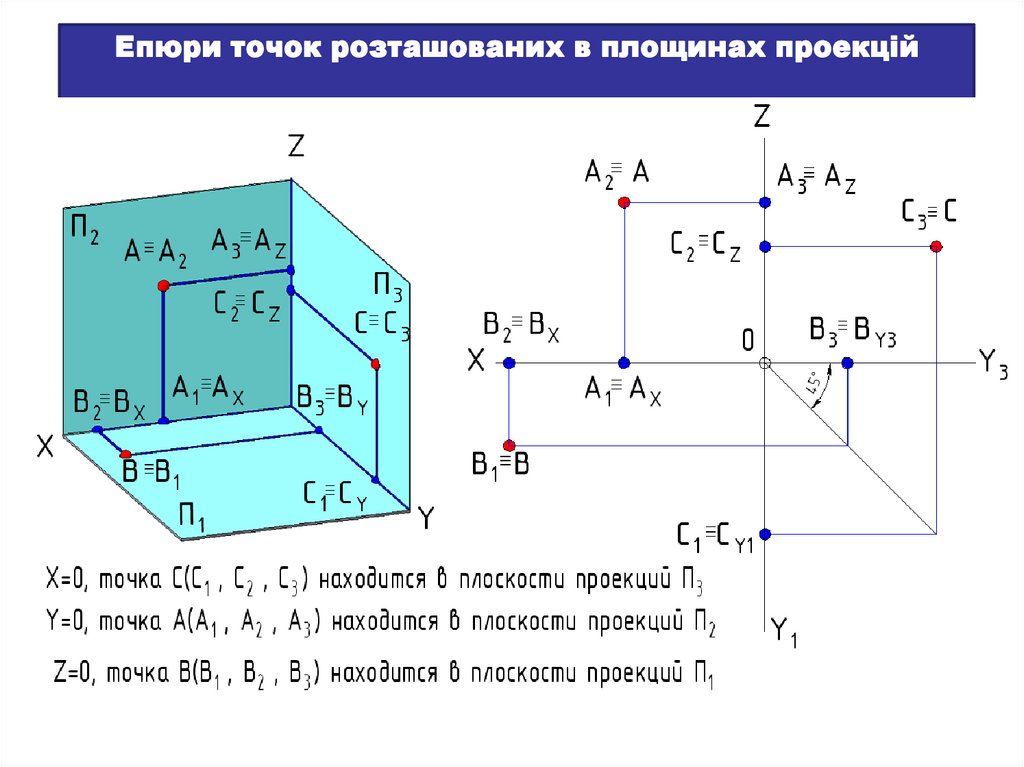
Епюри точок розташованих в площинах проекцій

24.

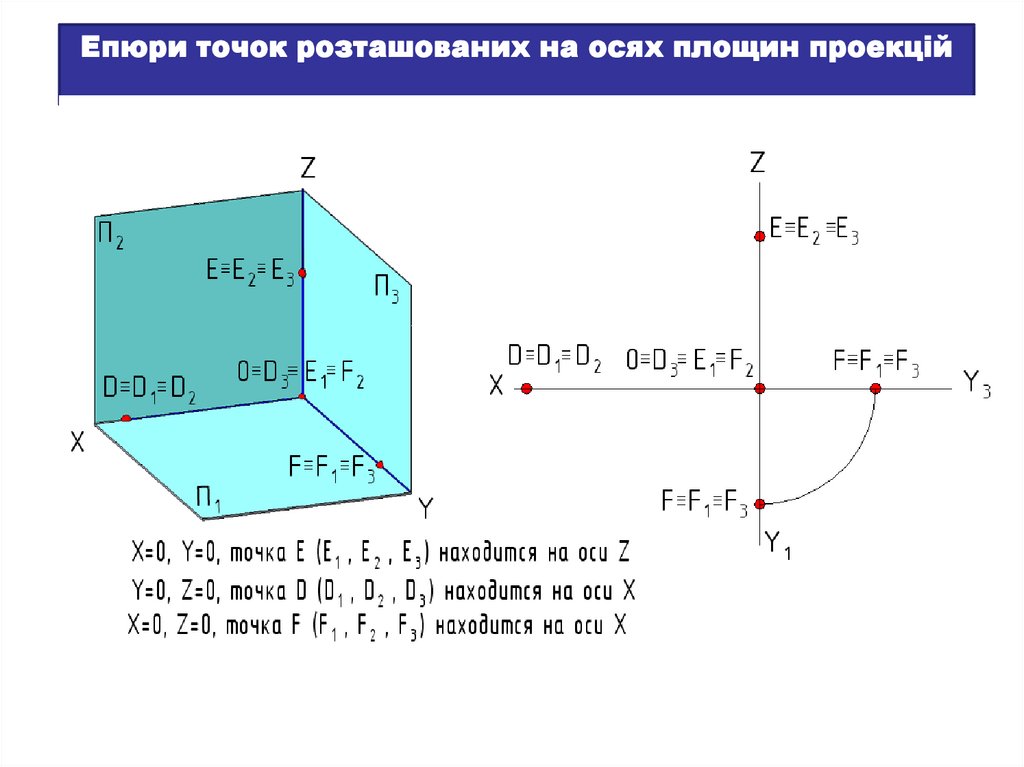
Епюри точок розташованих на осях площин проекцій

25.

Епюр точки розташованої в першому октанті
Координати X, Y, Z позитивні

26.

Епюр точки розташованої в другому октанті
Координати X, Y, Z - негативні

27.

Епюр точки розташованої в третьому октанті
Координати X - ПОЗИТИВНА, Y, Z - НЕГАТИВНІ

28.

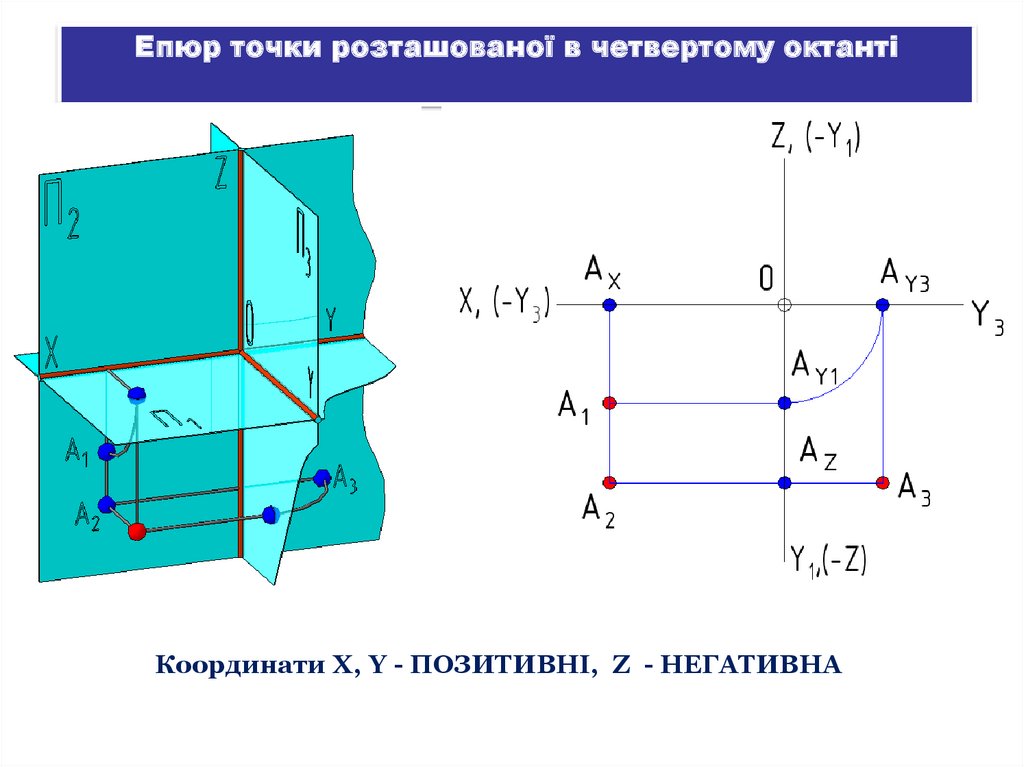
Епюр точки розташованої в четвертому октанті
Координати X, Y - ПОЗИТИВНІ, Z - НЕГАТИВНА

29.

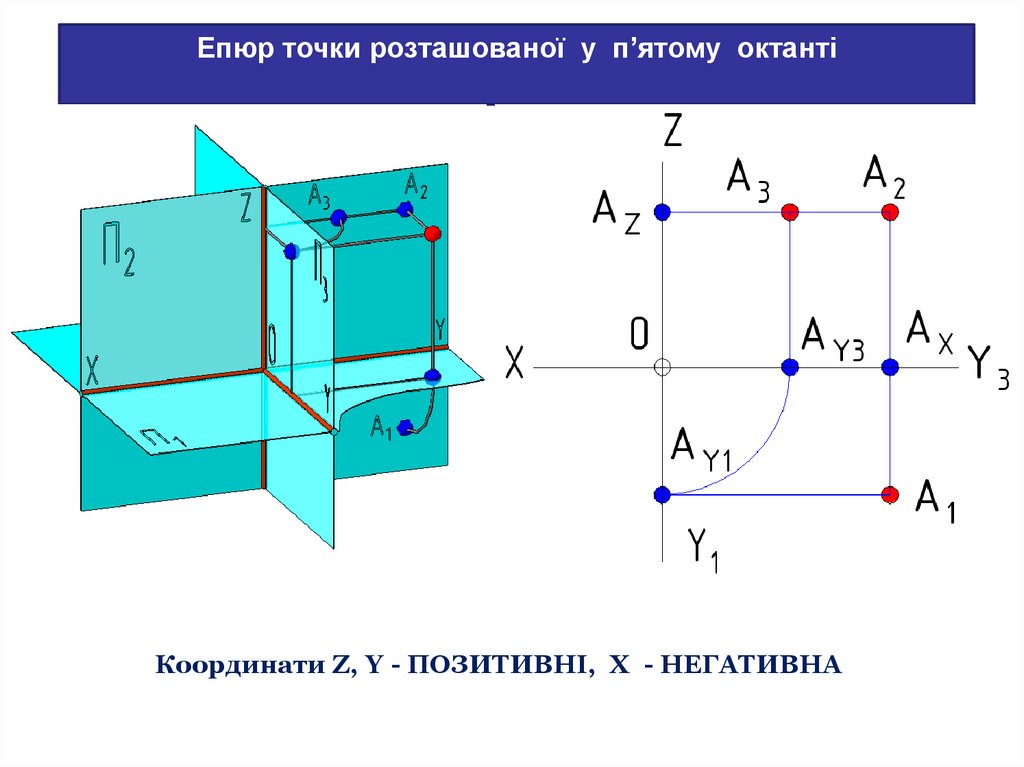
Епюр точки розташованої у п’ятому октанті
Координати Z, Y - ПОЗИТИВНІ, X - НЕГАТИВНА

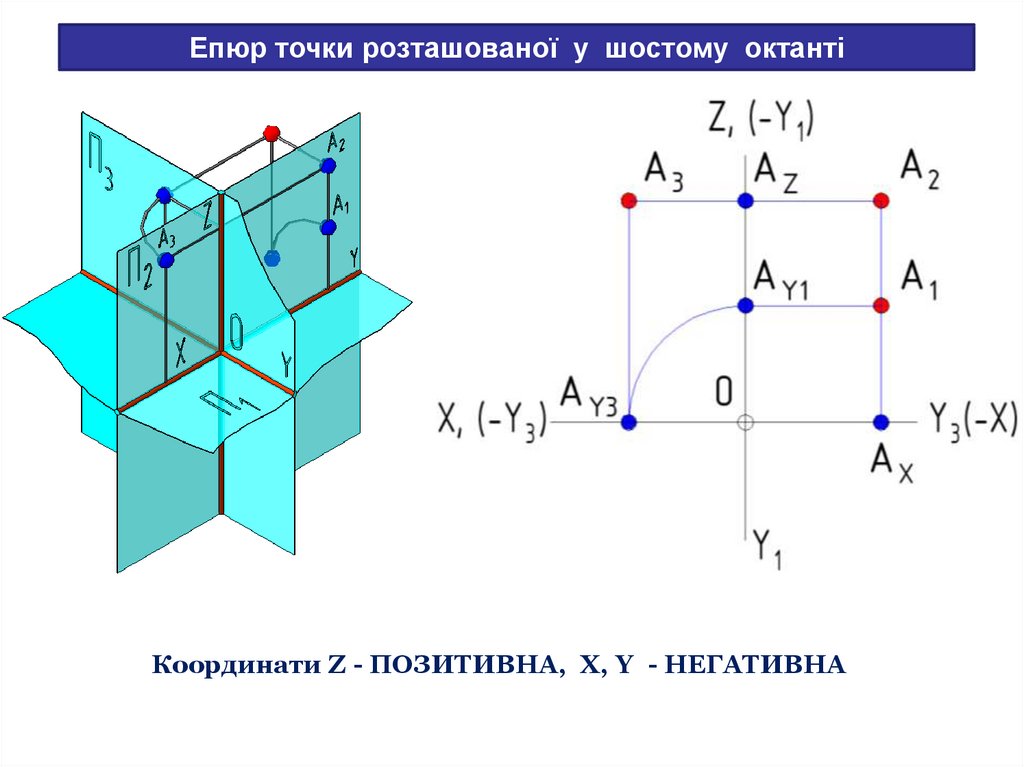
30.

Епюр точки розташованої у шостому октанті
Координати Z - ПОЗИТИВНА, X, Y - НЕГАТИВНА

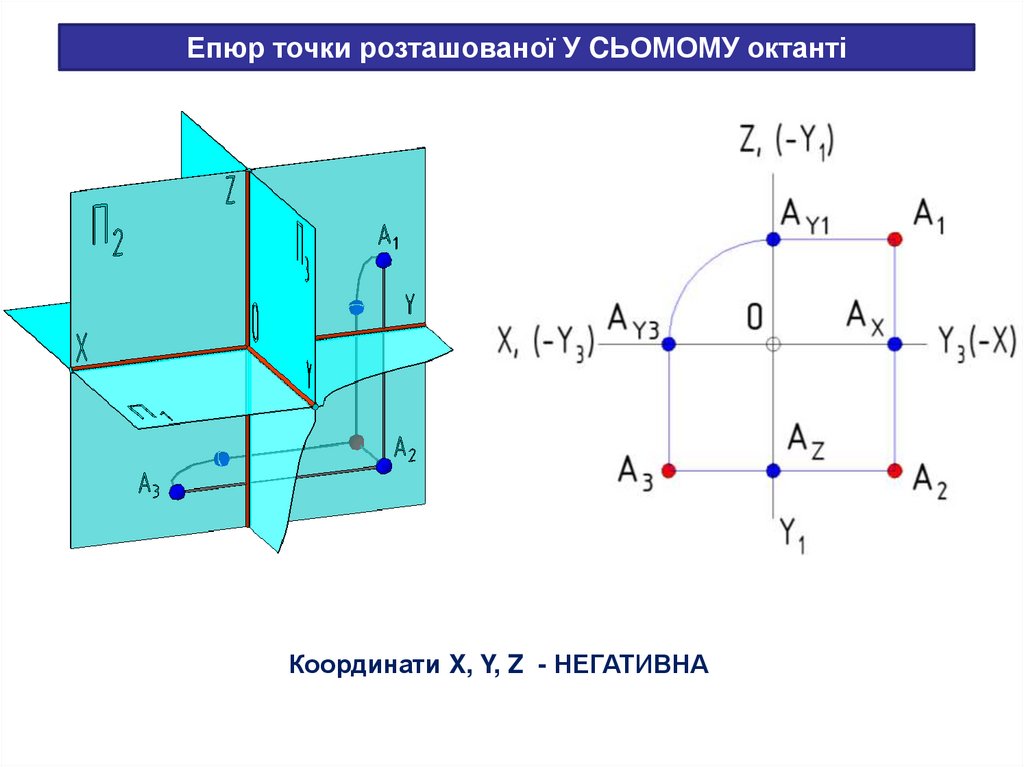
31.

Епюр точки розташованої У CЬОМОМУ октанті
Координати X, Y, Z - НЕГАТИВНА

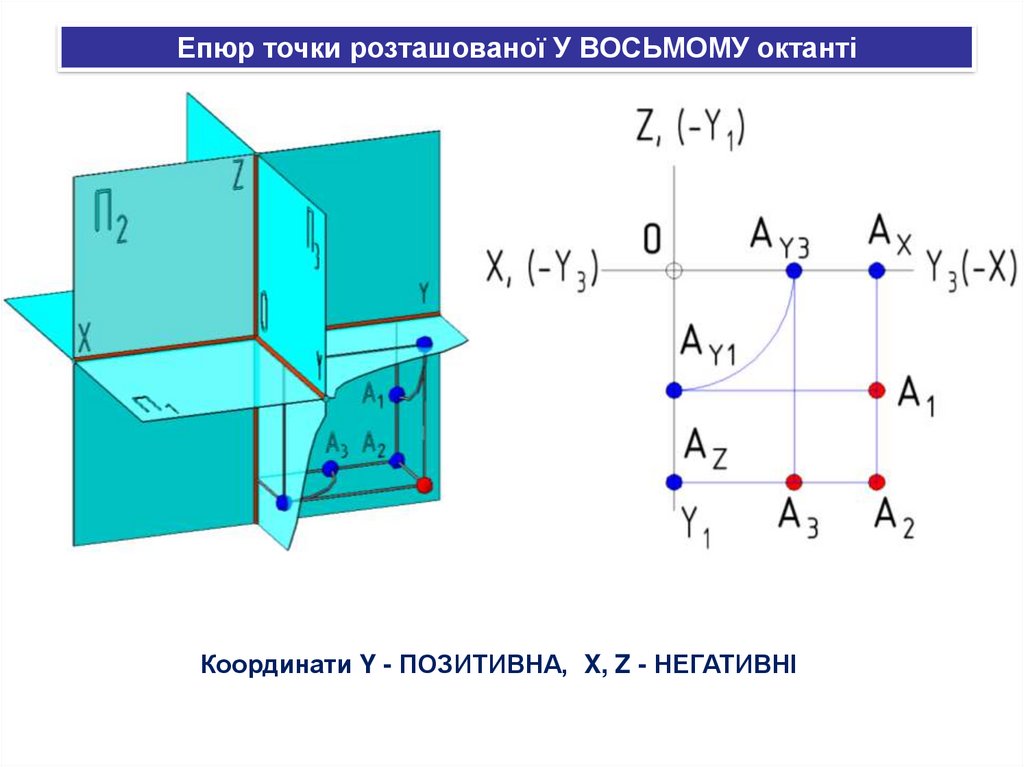
32.

Епюр точки розташованої У ВОСЬМОМУ октанті
Координати Y - ПОЗИТИВНА, X, Z - НЕГАТИВНІ

33.

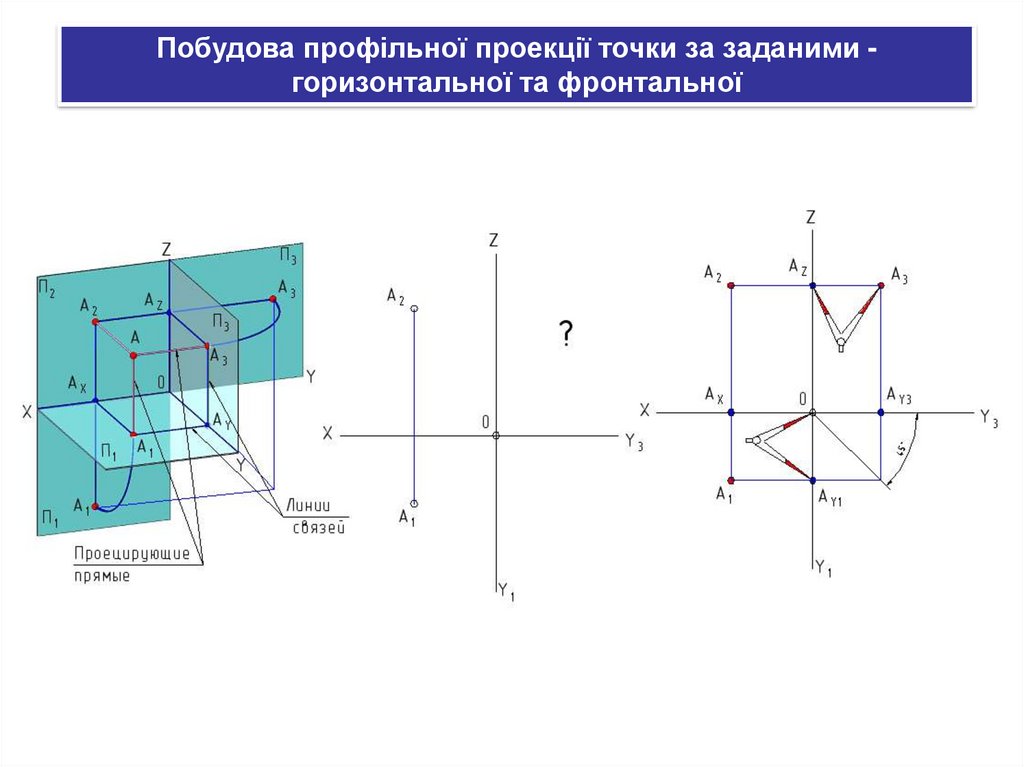
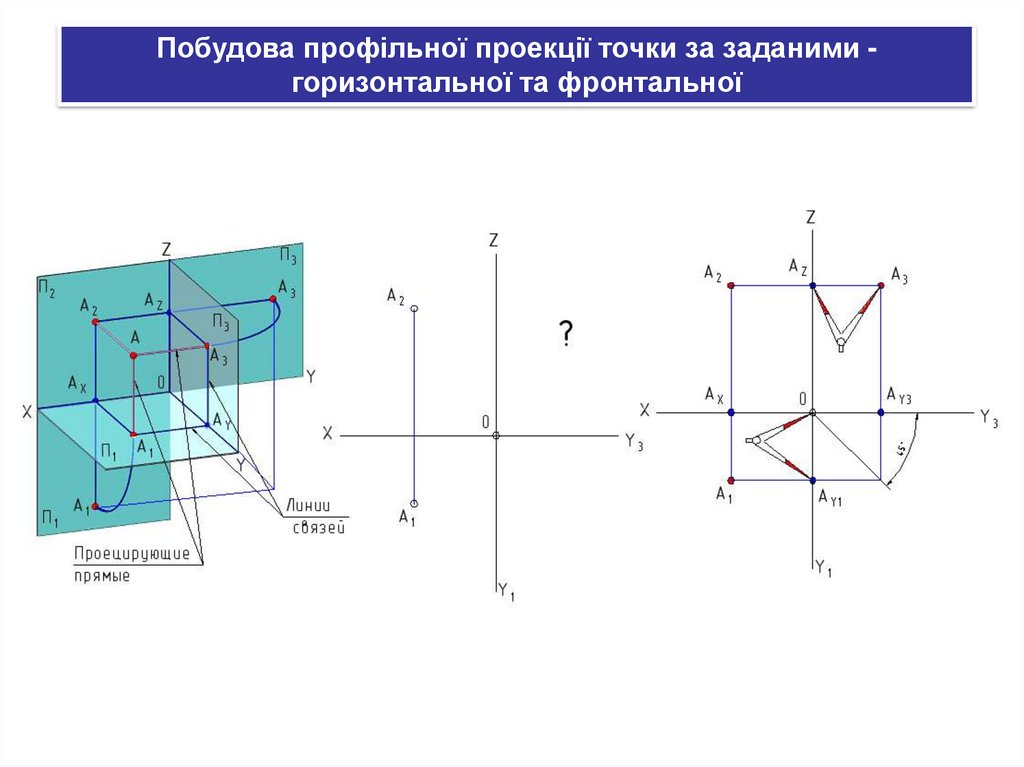
Побудова профільної проекції точки за заданими горизонтальної та фронтальної

34.

Побудова профільної проекції точки за заданими горизонтальної та фронтальної

35.

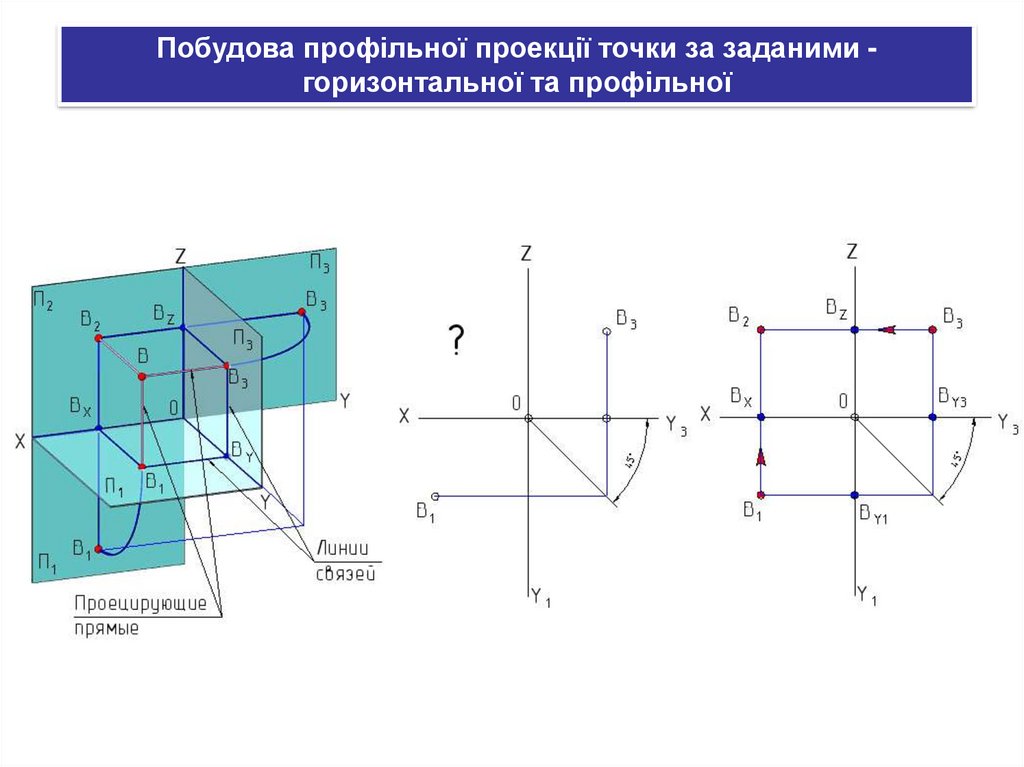
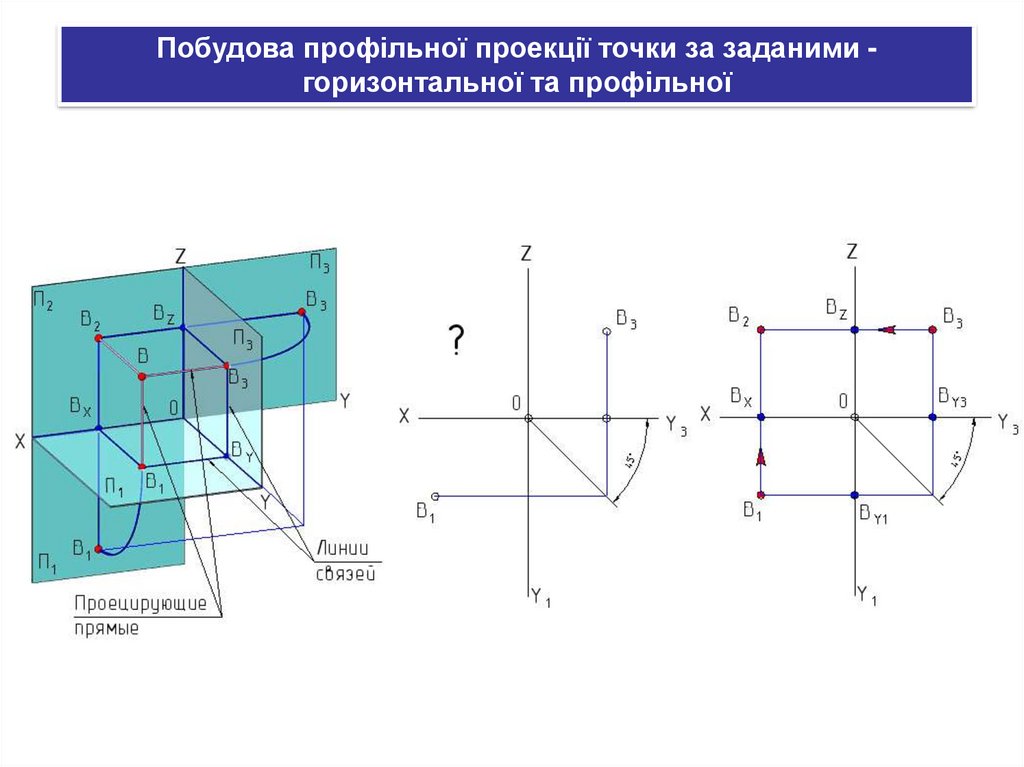
Побудова профільної проекції точки за заданими горизонтальної та профільної

36.

Побудова профільної проекції точки за заданими горизонтальної та профільної

37.

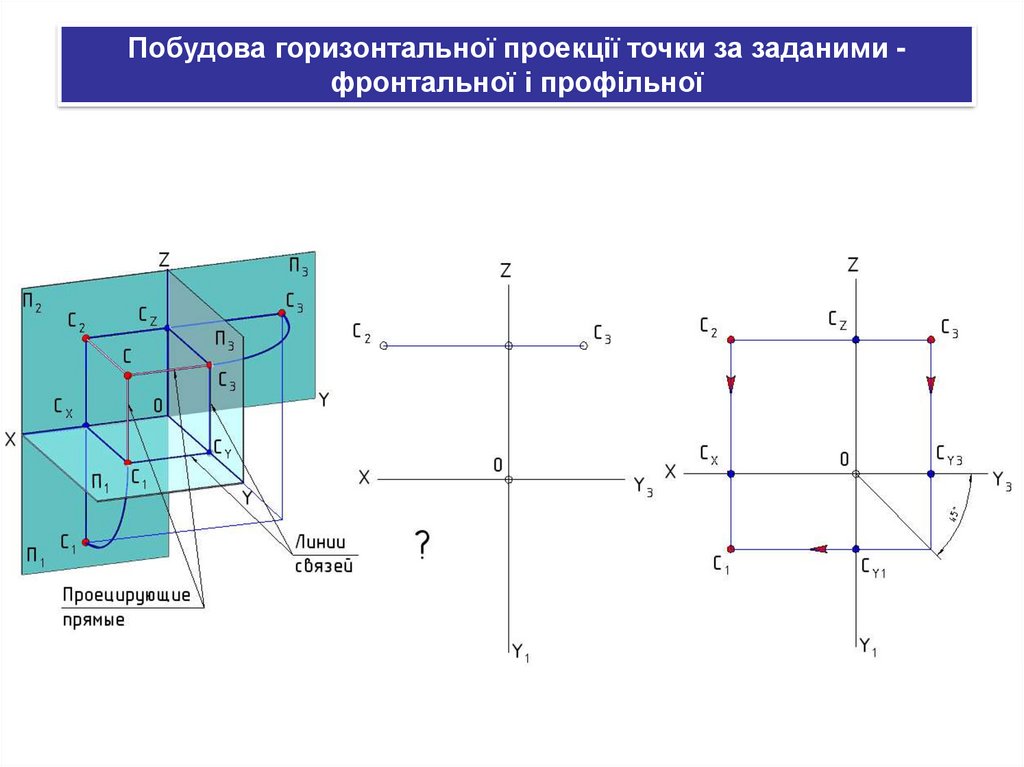
Побудова горизонтальної проекції точки за заданими фронтальної і профільної

38.

Положення прямої відносно площин
проекцій
Відносно площин проекцій пряма
може займати безліч положень. Ці
положення можна систематизувати
і розділити на прямі окремого і
загального положення.
Прямі окремого положення
поділяються на проектуючі прямі і

39.

Положення прямої відносно площин
проекцій
Проектуючою прямою називають пряму, яка
перпендикулярна до однієї площини проекцій і
паралельна до двох інших.
Основні властивості проектуючої прямої.
На одну із площин проекцій проектуюча пряма
проектується в точку, а на дві інших у вигляді
відрізків, які займають вертикальне або
горизонтальне положення і величина яких
дорівнює натуральній величині відрізка прямої.

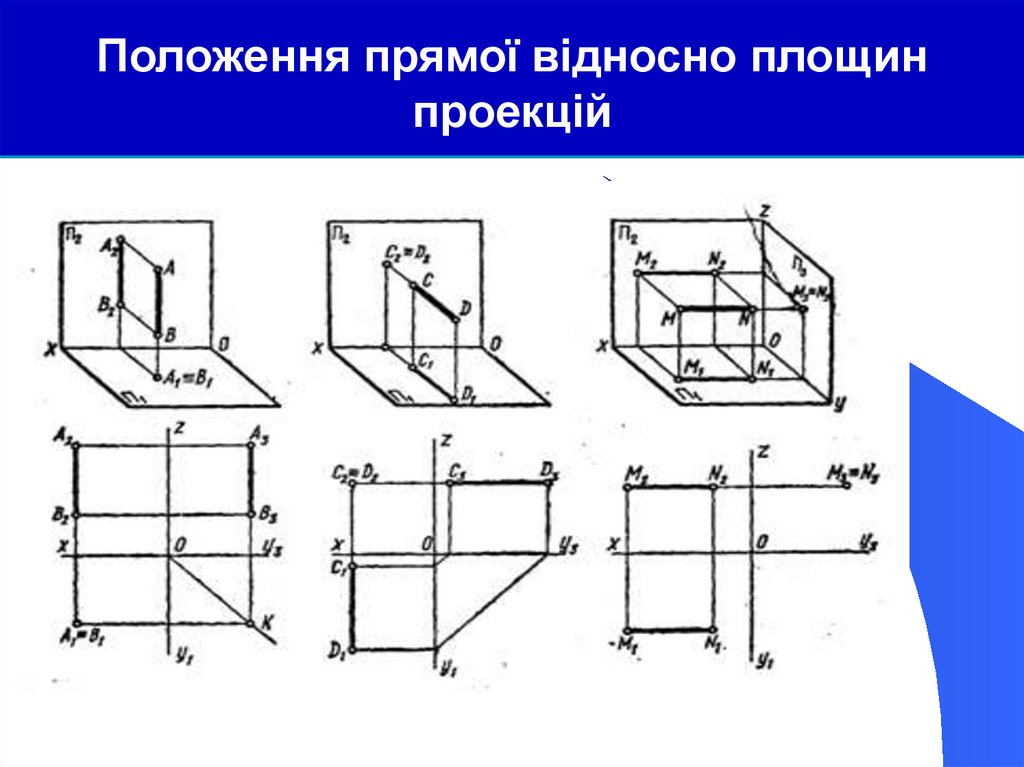
40.

Положення прямої відносно площин
проекцій
На рис а пряма АВ перпендикулярна до
горизонтальної площини проекцій і називається
горизонтально проектуючою прямою, пряма СD
(рис. б) перпендикулярна до фронтальної площини
проекцій і називається фронтально проектуючою,
пряма MN (рис. в) перпендикулярна до
профільної площини проекцій і називається
профільно проектуючою прямою

41.

Положення прямої відносно площин
проекцій

42.

Положення прямої відносно площин
проекцій
Прямими рівня називають прямі, паралельні
одні із площин проекцій.
Пряма АВ (рис. а) паралельна до
горизонтальної площини проекцій і
називається горизонтальною прямою, пряма
CD (рис. 160 б) паралельна фронтальній
площині проекцій і називається фронтальною
прямою, пряма MN (рис. в) паралельна
профільній площині проекцій і називається
профільною прямою

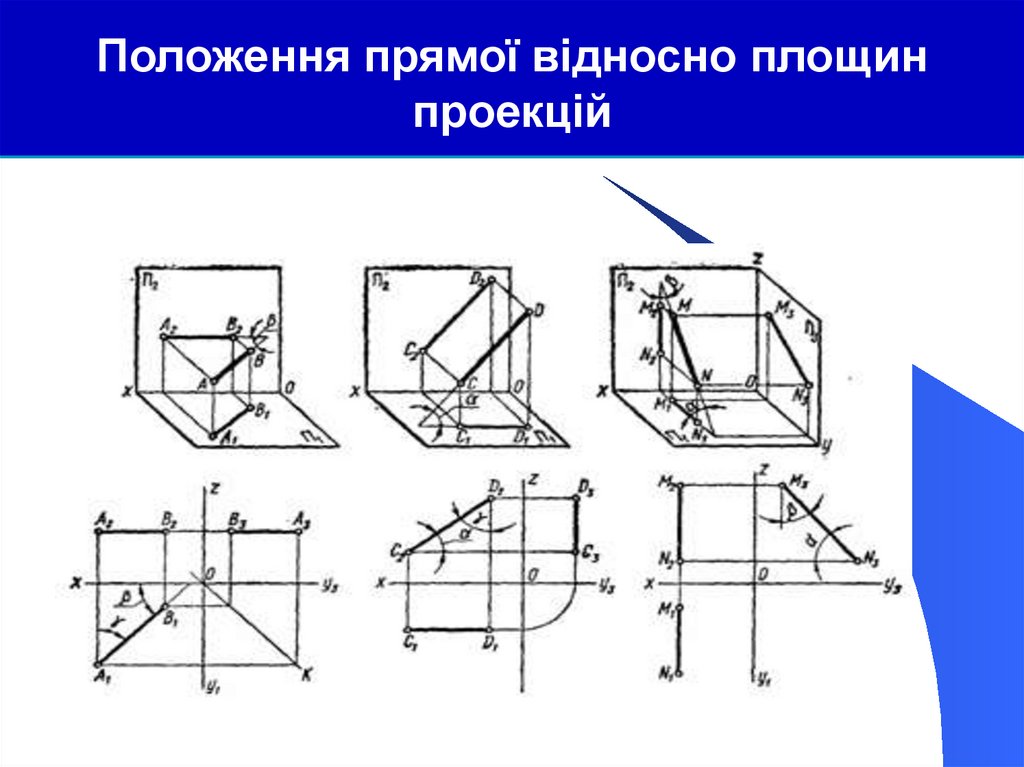
43.

Положення прямої відносно площин
проекцій

44.

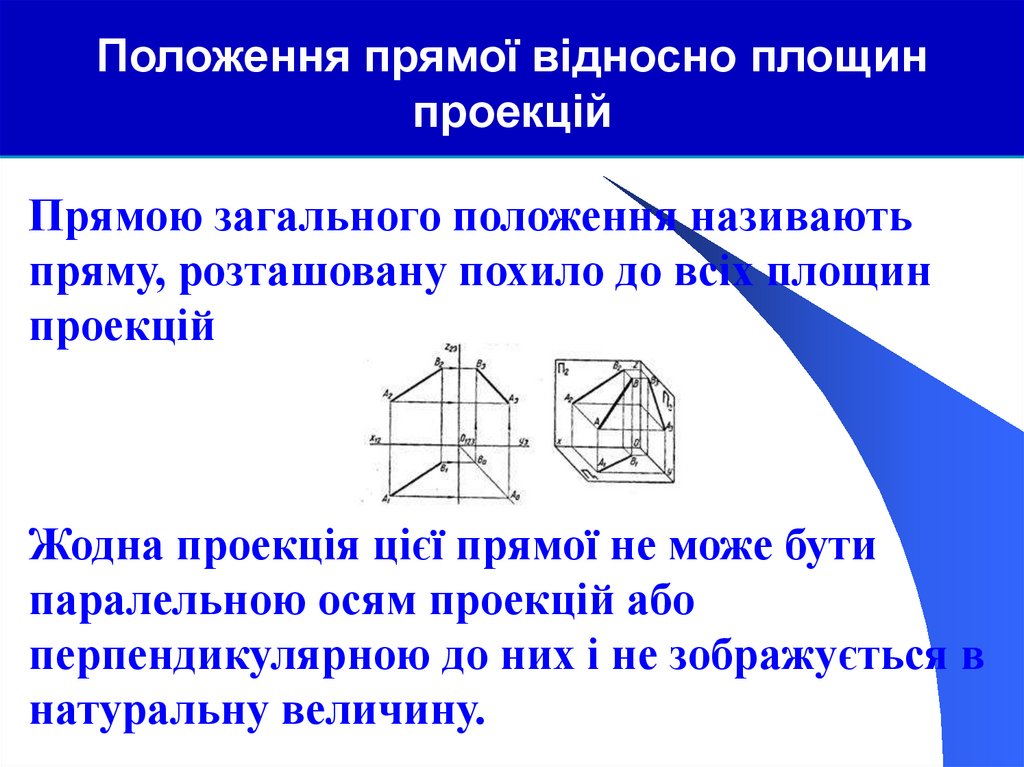
Положення прямої відносно площин
проекцій
Прямою загального положення називають
пряму, розташовану похило до всіх площин
проекцій
Жодна проекція цієї прямої не може бути
паралельною осям проекцій або
перпендикулярною до них і не зображується в
натуральну величину.

45.

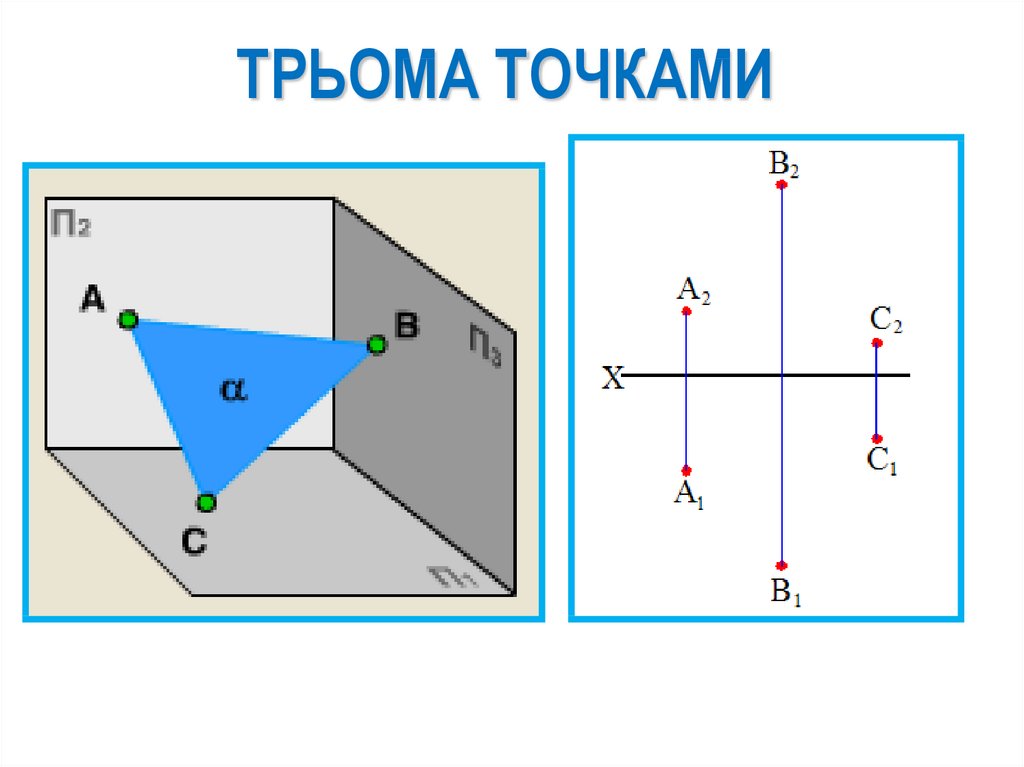
СПОСОБИ ЗАВДАННЯ ПЛОЩИН
НА КРЕСЛЕНИКУ
Для графічного завдання площини
досить задати проекції трьох
ії точок, які не належать одній
прямій.

46.

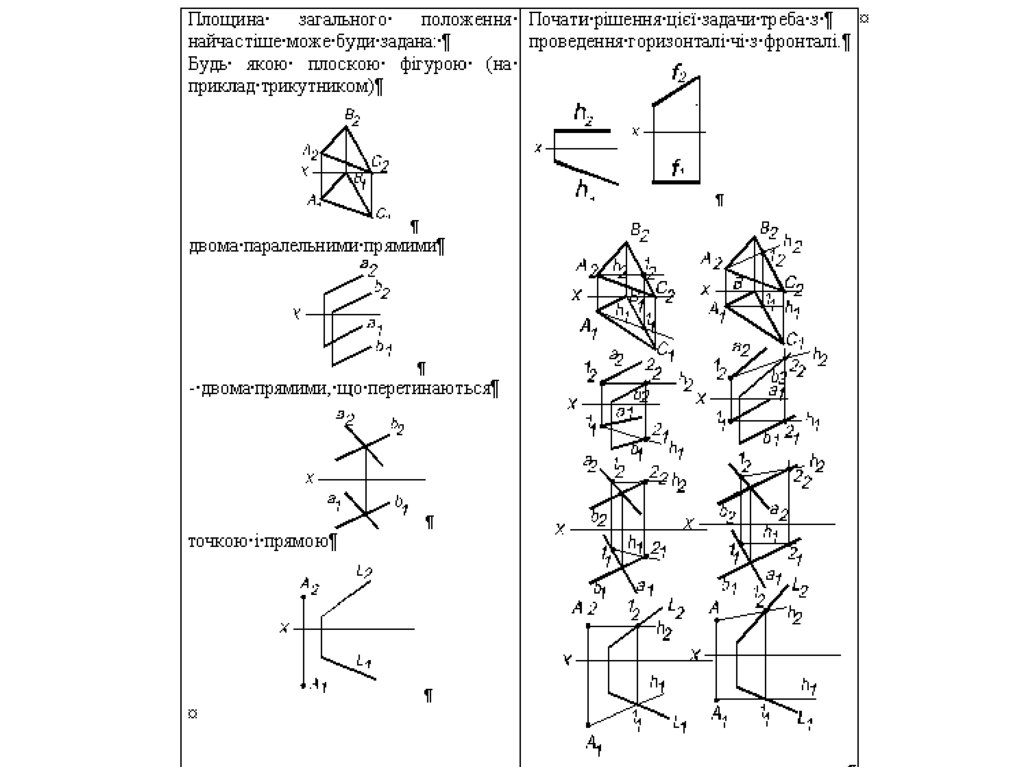
ТРЬОМА ТОЧКАМИ

47.

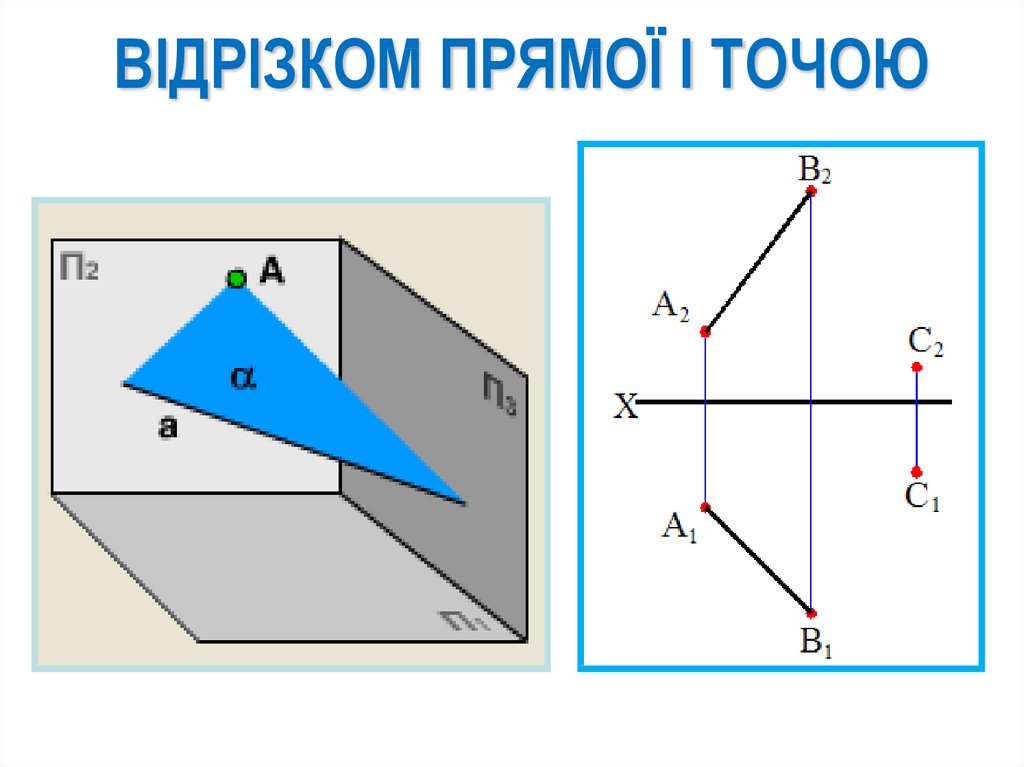
ВІДРІЗКОМ ПРЯМОЇ І ТОЧОЮ

48.

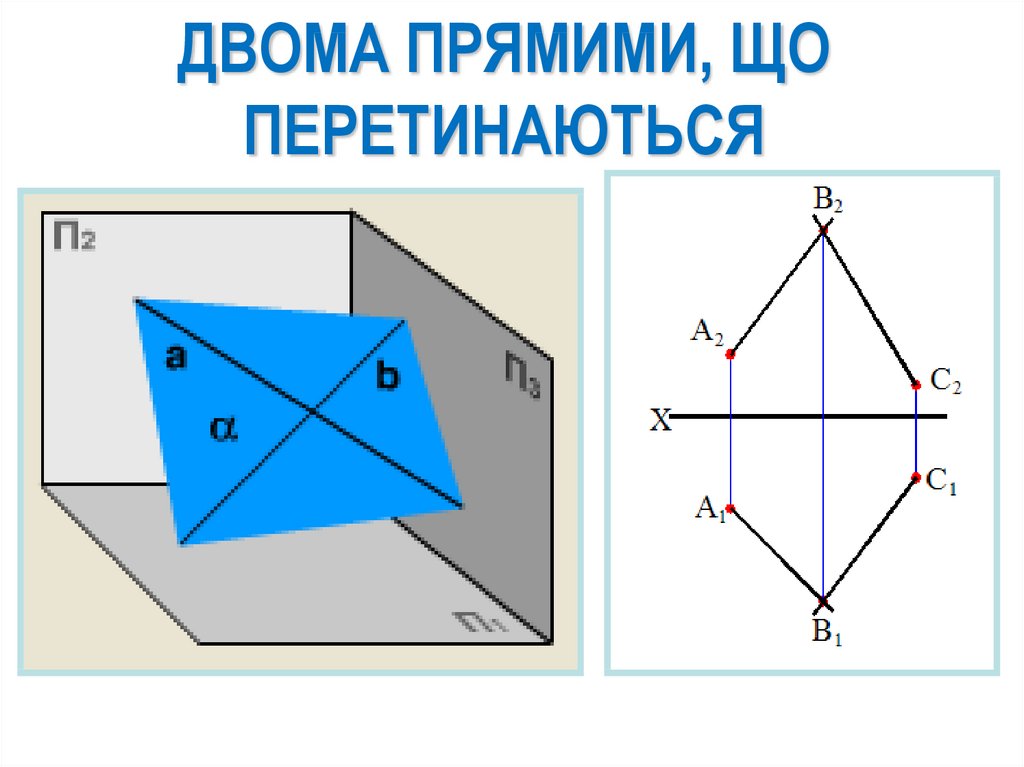
ДВОМА ПРЯМИМИ, ЩО
ПЕРЕТИНАЮТЬСЯ

49.

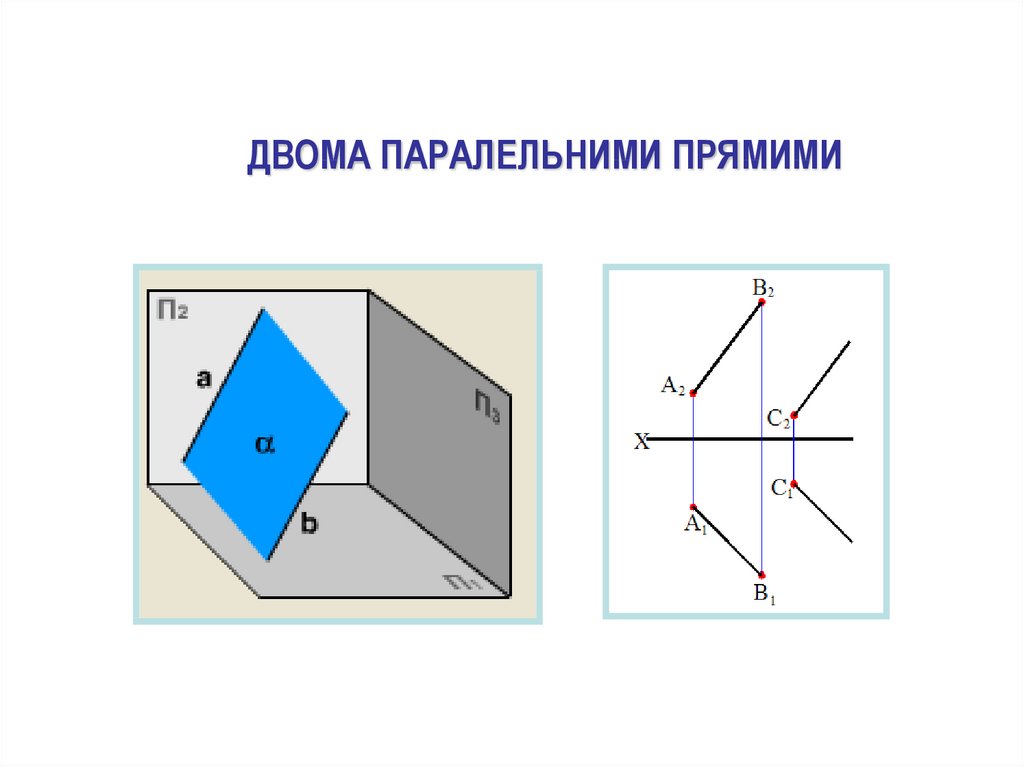
ДВОМА ПАРАЛЕЛЬНИМИ ПРЯМИМИ

50.

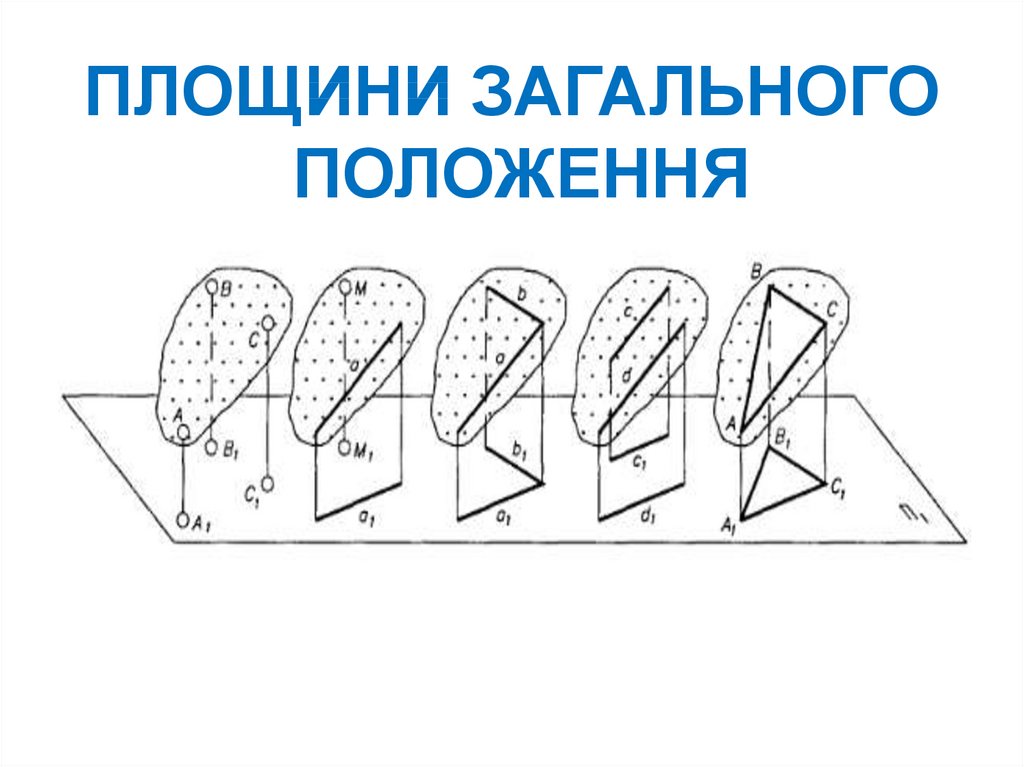
ПЛОЩИНИ ЗАГАЛЬНОГО
ПОЛОЖЕННЯ

51.

ПЛОЩИНИ РІВНЯ
ГОРИЗОНТАЛЬНА ПЛОЩИНА
Σ||∏1 α=0˚ β=90 ˚
ФРОНТАЛЬНА ПЛОЩИНА
Σ||∏2 β=0˚ α=90˚
ПРОФІЛЬНА ПЛОЩИНА
Σ||∏3 α=90˚ β=90˚

52.

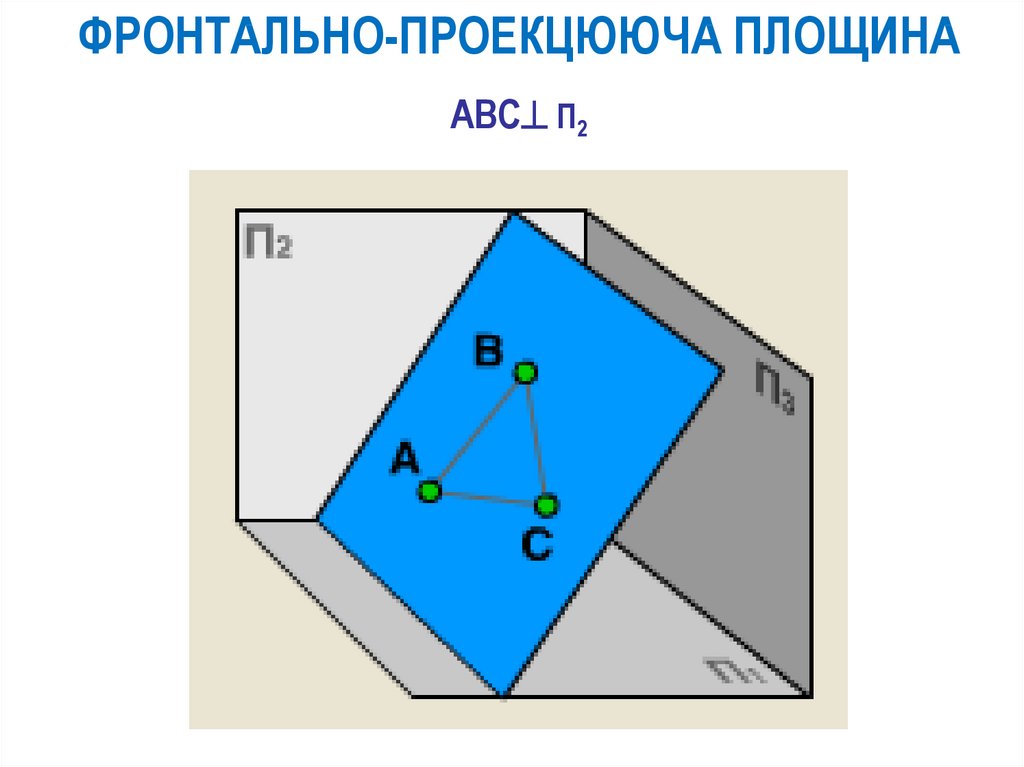
ФРОНТАЛЬНО-ПРОЕКЦЮЮЧА ПЛОЩИНА
ABC П2

53.

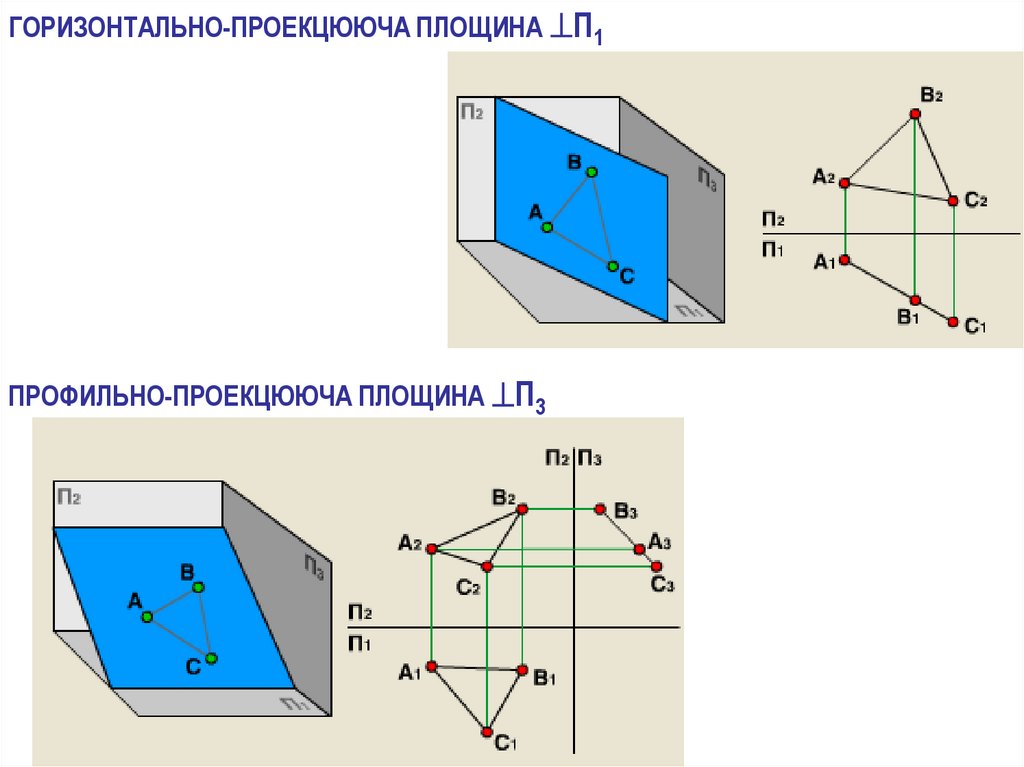
ГОРИЗОНТАЛЬНО-ПРОЕКЦЮЮЧА ПЛОЩИНА П1
ПРОФИЛЬНО-ПРОЕКЦЮЮЧА ПЛОЩИНА П3

54.

Задача: Площина загального положення задана
плоскою фігурою – трикутником.
Знайти натуральну величину трикутника за
допомогою метода заміни площин проекцій.
Щоб знайти натуральну величину площини загального
положення, треба перетворити ії у площину рівня. Для цього
треба виконати дві заміни.
Увага ! На всі поставлені питання треба обов’язково дати
відповідь. Якщо відповідь дати складно, питання треба
запам’ятати чи записати і обов’язково запитати у викладача.

55.

Треба починати з аналізу положення трикутника в системі
площин проекцій.
1. Якщо задана площина паралельна до основної площини
проекцій, то вона проекцюється на цю площину проекцій без
спотворення, тобто в натуральну величину.
Трикутник розташований паралельно до площини проекцій П2.
У цьому випадку натуральна величина трикутника визначається
за його фронтальною проекцією на площину П2. Трикутник
належить площині, яка має назву – площина рівня.

56.

2.Якщо площина трикутника перпендикулярна до
площини проекцій, то вона проекцюється на цю площину
проекцій у вигляді прямої лінії – сліду проекції, а на іншу
площину проекції спотворено.
У цьому разі треба зробити одну заміну площин проекцій, щоб
знайти натуральну величину заданої плоскої фігури.
ЯК ? – паралельно до площини заданої плоскої фігури
розташувати нову площину проекцій П4 за умовою, що вона
буде перпендикулярна до тієї площини проекцій, що
залишається в системі площин проекцій (тобто, або площини
П1 чи площини П2).

57.

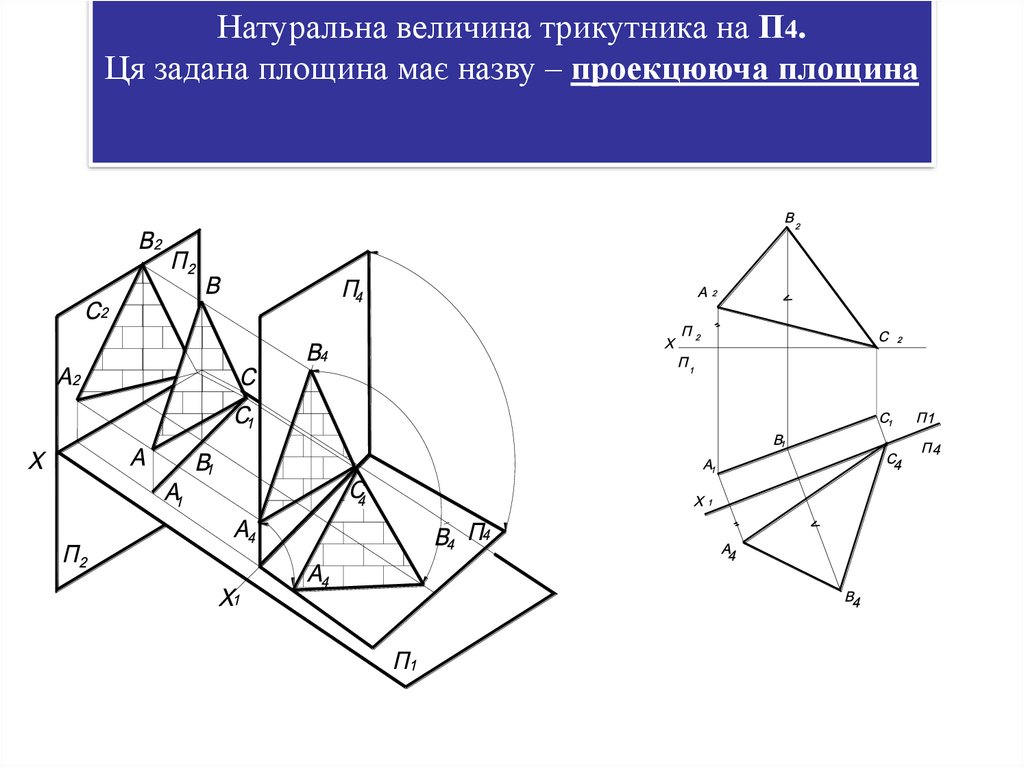
Натуральна величина трикутника на П4.
Ця задана площина має назву – проекцююча площина

58. 1 заміна – спочатку перетворити площину загального положення на проекцюючу. Для цього треба провести в площині трикутника лінію

Щоб знайти натуральну величину площини загального положення, треба
перетворити ії у площину рівня. Для цього треба виконати дві заміни.
1 заміна – спочатку перетворити площину загального положення на
проекцюючу.
Для цього треба провести в площині трикутника лінію рівня, наприклад
горизонталь і розташувати допоміжну площину проекцій перпендикулярно
до неї. Після виконаних побудов, площина загального положення
проекцюється у вигляді лінії – сліду проекції.
проекцюючу.

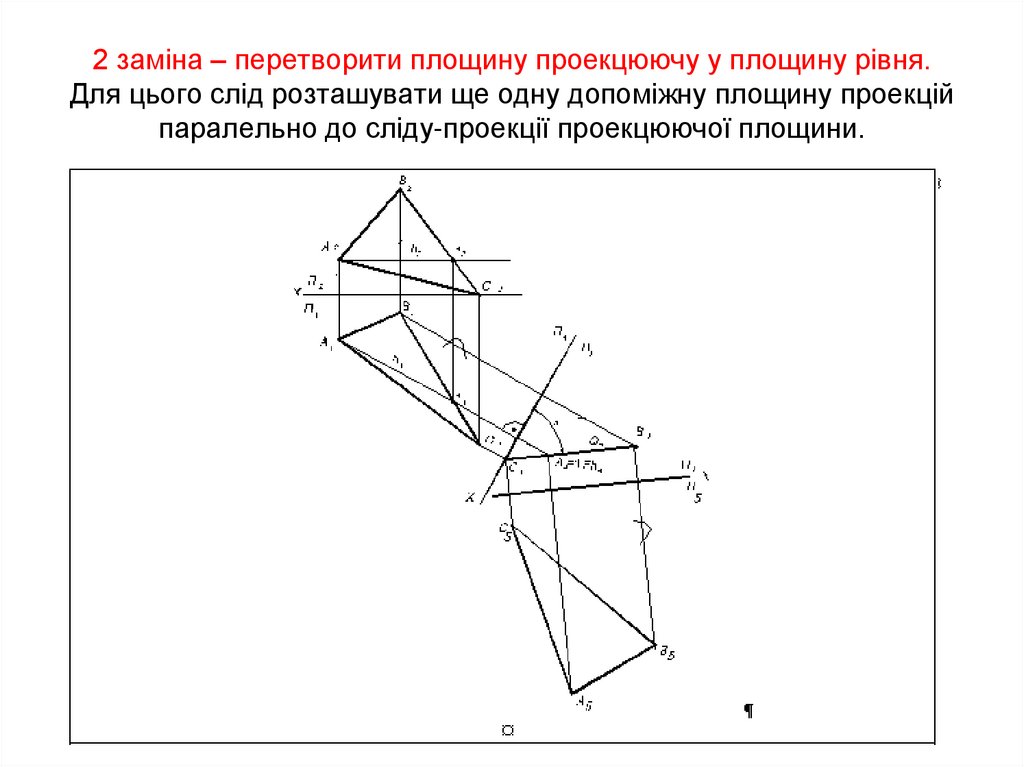
59. 2 заміна – перетворити площину проекцюючу у площину рівня. Для цього слід розташувати ще одну допоміжну площину проекцій

паралельно до сліду-проекції проекцюючої площини.

60.

В2
А2
h2
12
С2
Х П2
П1
В1
К1
А1
Показана побудова центра кола,
описаного навколо НВ трикутника. Центр
знаходиться на перетині
перпендикулярів, яки проведені з
середини двох сторін трикутника.
Проекція кола на П1 є еліпс - велика вісь
якого дорівнюється розміру діаметра
кола, а мала вісь знаходиться
проекцююванням точки К на П1.
O1
К4
α
11
h1
П4
X2
П5
B4
А4=14=h4
O4
С1
С4
К5
С5
П1
O5
П4
X1
В5
А5

61.

X26
П6
П2
В6
β
R 22
f2
R О2
R
О1
21
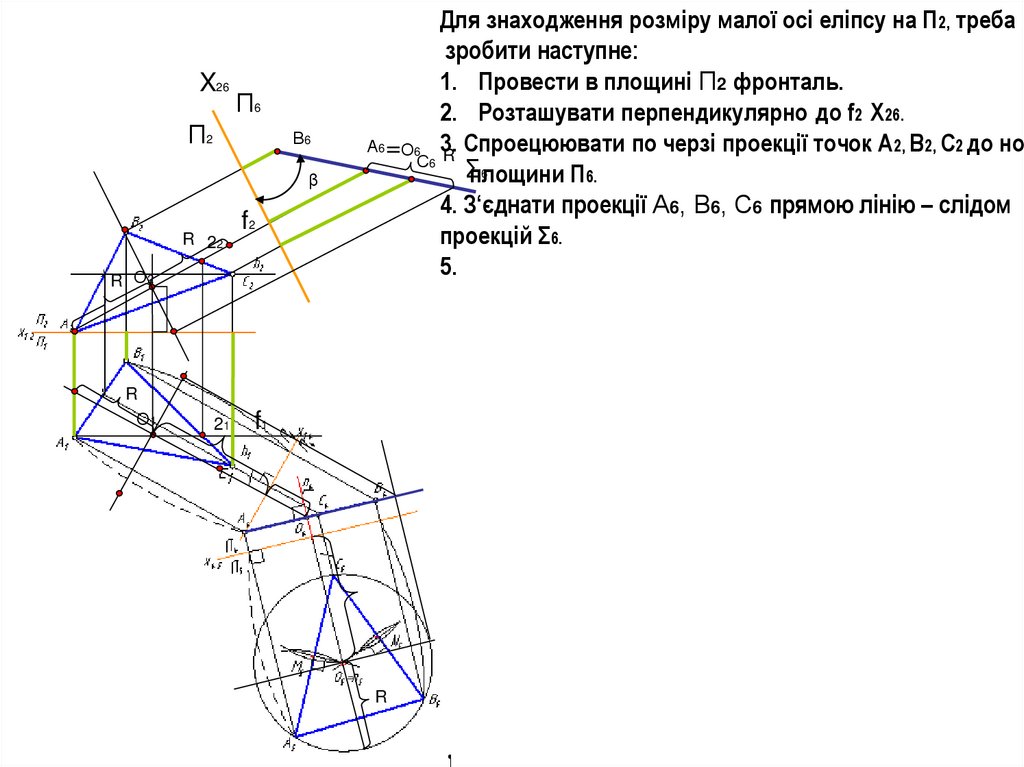
Для знаходження розміру малої осі еліпсу на П2, треба
зробити наступне:
1. Провести в площині П2 фронталь.
2. Розташувати перпендикулярно до f2 Х26.
А6 =О6 3. Спроецюювати по черзі проекції точок А2, В2, С2 до нов
С6 R
Σплощини
6
П6.
4. З‘єднати проекції А6, В6, С6 прямою лінію – слідом
проекцій Σ6.
5.
f1
R